Matemtica e suas Tecnologias Matemtica Ensino Fundamental 6

Matemática e suas Tecnologias - Matemática Ensino Fundamental, 6º Ano Medida de volume – conceitos iniciais

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais 1. Introdução

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Medidas de Volume

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Medida de Volume MEDIDAS Todos os dias, nós compramos, usamos ou medimos produtos que são vendidos de acordo com seu volume.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Medida de Volume MEDIDAS Quando falamos em volume, estamos nos referindo ao espaço ocupado por um corpo sólido, por um líquido ou por um gás.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Medida de Capacidade MEDIDAS Exemplos de nosso cotidiano: Quando você vai comprar um caminhão-pipa de água potável, deve observar a capacidade que corresponde ao reservatório de sua casa e a capacidade do caminhão.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Medida de Volume MEDIDAS Exemplos de nosso cotidiano: A conta de água de sua residência lhe informa a medida de volume de água que foi gasto. Observe o modelo de uma conta. Imagem: Vania Teofilo / Creative Commons Attribution-Share Alike 3. 0 Unported

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Medida de Volume MEDIDAS Exemplos de nosso cotidiano: Na sua casa, os reservatórios de água também podem ser em tamanhos diferentes.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Medida de Volume MEDIDAS Exemplos de nosso cotidiano: Para medir a quantidade de ar que ocupa uma sala ou o espaço que uma quantidade de livros ocupa em uma caixa, também calculamos o volume.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Conceitos importantes O QUE É MEDIR ? O QUE É GRANDEZA? O QUE É UNIDADE DE MEDIDA?

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais O QUE É MEDIR ? É associar valores numéricos às grandezas, através de instrumentos. O QUE É GRANDEZA ? É tudo aquilo que pode ser medido.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais MEDIR É comparar a grandeza a ser medida com outra de mesma espécie, considerada padrão e denominada. UNIDADE DE MEDIDA Toda medida é constituída de um número e de uma unidade padrão.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais VOLUME É uma das grandezas mais comuns e mais utilizadas no nosso cotidiano. Está sempre presente no nosso dia a dia. No Sistema Internacional A grandeza volume tem como unidade base o metro cúbico (m³).

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Volume É, então, a medida que quantifica o espaço ocupado por um objeto.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Capacidade Logo, podemos dizer que a quantidade de um líquido ou de um gás que ocupa o volume interno de um recipiente utilizado é igual à sua capacidade.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Metro Cúbico O sistema métrico adota o metro cúbico (m³) como unidade-padrão de medida de volume.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Metro Cúbico Metro cúbico (m³) é a medida equivalente ao espaço ocupado por um cubo de 1 metro de aresta (lado). 1 m Cubo 1 m 1 m Os contornos em um cubo são as arestas, e o volume do cubo é de 1 m³.

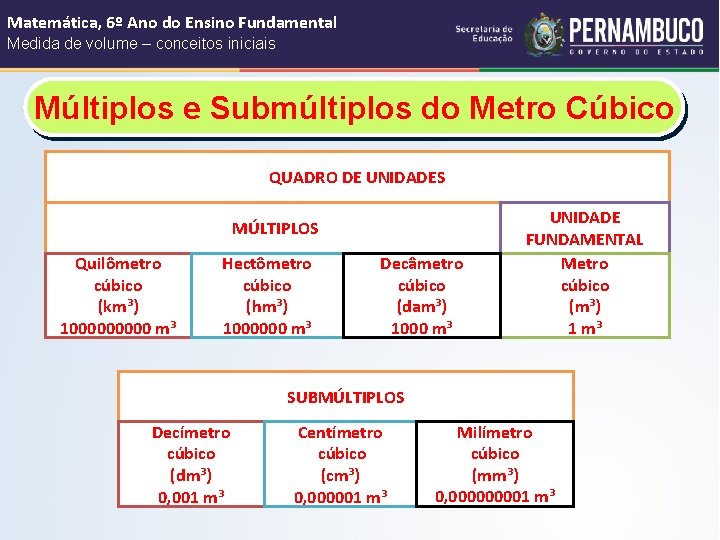
Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Unidades de Medidas de Volume Além do metro cúbico, utilizamos também seus múltiplos e submúltiplos.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Múltiplos e Submúltiplos do Metro Cúbico QUADRO DE UNIDADES MÚLTIPLOS Quilômetro cúbico (km³) 100000 m³ Hectômetro cúbico (hm³) 1000000 m³ Decâmetro cúbico (dam³) 1000 m³ UNIDADE FUNDAMENTAL Metro cúbico (m³) 1 m³ SUBMÚLTIPLOS Decímetro cúbico (dm³) 0, 001 m³ Centímetro cúbico (cm³) 0, 000001 m³ Milímetro cúbico (mm³) 0, 00001 m³

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais OBSERVAÇÃO Você percebeu que cada unidade é 1000 vezes maior que a anterior a ela? No sistema métrico decimal, cada 1000 unidades de volume equivalem a 1 unidade de volume imediatamente superior. Veja: 1 000 m³ = 1 dam³ 1 000 cm³= 1 dm³

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais OBSERVAÇÃO A unidade de medida que será escolhida depende de cada situação. Exemplos: Para medir o volume de uma piscina, usaremos o m³. Para medir o volume de uma caixa onde serão colocados livros, usaremos o cm³.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Medidas de Volume As unidades de medida de volume mais utilizadas são o cm³ e o m³. LEMBRETE

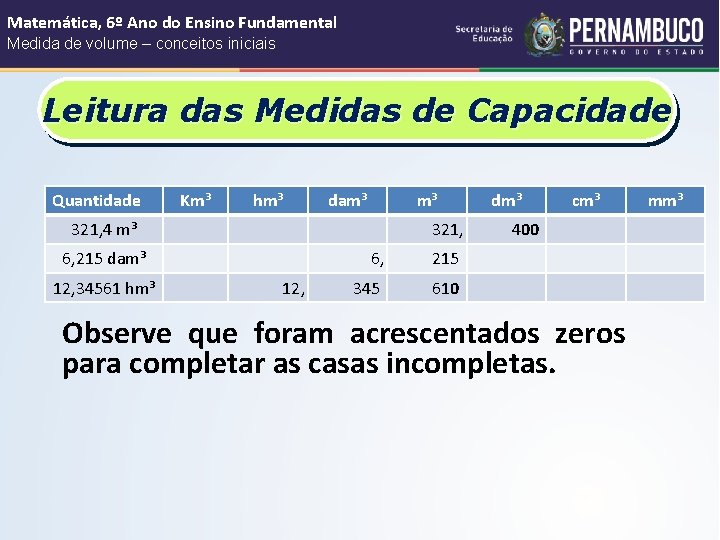
Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Leitura das Medidas de Volume A leitura das medidas de volume é feita da mesma forma que a das unidades de medidas de superfície. Observação: Em cada unidade do quadro, ficarão 3 algarismos. Se houver casas incompletas à direita, completaremos com zeros.

Matemática, 6º Ano Medida de volume – conceitos iniciais Leitura das Medidas de Volume Com a ajuda do quadro de medidas, fica mais simples fazermos a leitura. Vejamos alguns exemplos:

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Leitura das Medidas de Capacidade Quantidade Km³ hm³ dam³ m³ 321, 4 m³ 321, 6, 215 dam³ 12, 34561 hm³ 12, 6, 215 345 610 dm³ cm³ 400 Observe que foram acrescentados zeros para completar as casas incompletas. mm³

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Quantidade Km³ hm³ dam³ m³ 321, 4 m³ 321, 6, 215 dam³ 12, 34561 hm³ dm³ 12, 6, 215 345 610 cm³ mm³ 400 A leitura de cada número será expressa da seguinte forma: a 321, 400 m³ → trezentos e vinte e um metros cúbicos e quatrocentos decímetros cúbicos. b 6, 215 dam³ → seis decâmetros cúbicos e duzentos e quinze metros cúbicos. c 12, 345610 hm³ → doze hectômetros cúbicos, trezentos e quarenta e cinco mil, seiscentos e dez metros cúbicos.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Alerta!!! Devemos fazer a leitura das medidas de volume, agrupando os algarismos de 3 em 3. Imagem: Ladyof. Hats / Public Domain.

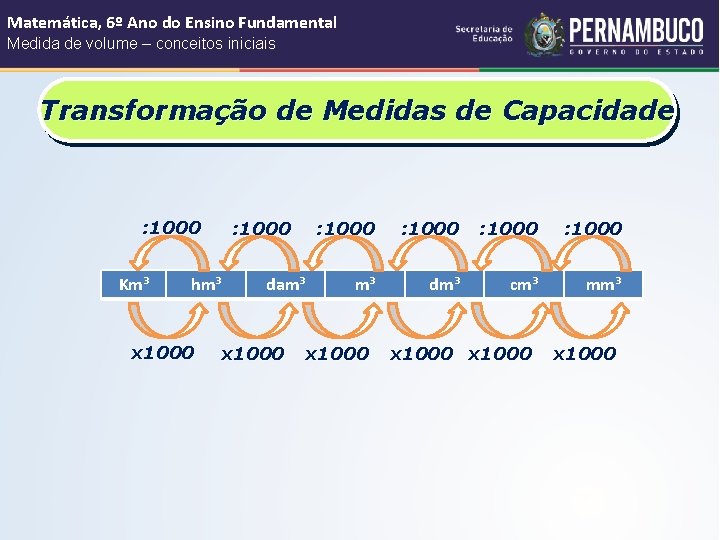
Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Transformação de Medidas de Capacidade Em nosso cotidiano, há ocasiões em que é necessário transformarmos uma unidade de volume em outra.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Transformação de Medidas de Capacidade É preciso lembrar, porém, que cada unidade de medida de volume é 1000 vezes maior que a unidade imediatamente à direita. Logo, sob cada unidade de medida, são colocados 3 algarismos.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Transformação de Medidas de Capacidade : 1000 Km³ : 1000 hm³ x 1000 dam³ x 1000 : 1000 m³ dm³ cm³ mm³ x 1000

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Vejamos, agora, exemplos. 1) Mário precisa transformar 20 m³ em cm³. Km³ hm³ dam³ m³ x 1000 dm³ cm³ mm³ x 1000 Mário deve multiplicar 1000 · 1000, ou seja: 1000000 Logo, teremos: 20 · 1000000 = 20000000 cm³.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Vejamos, agora, exemplos. 2) Matheus queria saber quantos dam³ equivaliam a 6543, 21 dm³. Km³ hm³ dam³ : 1000 m³ dm³ cm³ mm³ Matheus deve dividir por (1000 · 1000), ou seja: 1000000 Logo, teremos: 6543, 21 : 1000000 = 0, 00654321 dam³.

Matemática, 6º Ano do Ensino Fundamental Medida de volume – conceitos iniciais Exemplos de nosso dia a dia: a) Transformar 15 m³ de água em cm³ = 15 000 cm³. b) Transformar 15000000 dm³ de óleo em dam³ = 15 dam³. c) Transformar 2500000 mm³ de suco em m 3 = 25 m 3. d) Transformar 1 km 3 de areia em m³ = 100000 m³. e) Transformar 3, 5 m 3 de água em dm³ = 3 5000 dm³. f) Transformar 87 dm 3 de gás em mm³ = 87000000 litros.

REFERÊNCIAS BIBLIOGRÁFICAS SANTOS, Judson, 1974 – Matemática: 6º ano do ensino fundamental em nove anos/ Judson Santos, Annelise Maymone. – 2. ed. Revista e atualizada. – Recife: Prazer de Ler, 2009. p. 258 - 261. <http: //4. bp. blogspot. com/_gk. IR 0 OBMNg. M/TBAVqv. Kb_5 I/AAAABCA/ec. Aw. Caj. FYc. Q/s 1600 /professor 2. gif >. Acesso em 08 jul. 2012, 21: 58: 49. <http: //t 0. gstatic. com/images? q=tbn: ANd 9 Gc. SHFh. D 3 g 1 Wki. I 3 Umzaj. SYaj 9 NSWg. Ae. U 10 h 5 ED 0 t 9 n. Eq. W-Qx. YOmi >. Acesso em 09 jul. 2012, 21: 57: 06. <http: //jc 3. uol. com. br/blogs/repositorio/Nova%20 imagem(66). jpg >. Acesso em 09 jul. 2012, 21: 54: 37

Tabela de Imagens n° do direito da imagem como está ao lado da foto link do site onde se conseguiu a informação Data do slide Acesso 7 Vania Teofilo / Creative Commons http: //commons. wikimedia. org/wiki/File: Conta_com 06/11/2012 Attribution-Share Alike 3. 0 Unported. pesa. JPG 27 Ladyof. Hats / Public Domain. http: //commons. wikimedia. org/w/index. php? title=Fi 06/11/2012 le: Smiley_green_alien_wow. svg&page=1