Matemtica e suas Tecnologias Geometria Plana Ensino Mdio

Matemática e suas Tecnologias Geometria Plana Ensino Médio, 1º Série ngulos

Você sabia que. . . a reta é um conjunto infinito de pontos? . . . é usual representar os pontos por letras maiúsculas (A, B, C, . . . , M, N, . . . ) E as retas por letras minúsculas (r, s, t, . . . )? Obs: Nos conjuntos numéricos, a convenção é inversa: as letras Maiúsculas designam conjuntos e as letras minúsculas os seus elementos. . Por dois pontos distintos A e B, passa uma única reta r ou AB? • P A | C B | | r Reta: r ou AB Semi-retas: ou CA e ou CB AEe PɆr

. . . Na figura estão definidas as semi-retas CA e, CB cuja origem comum é o ponto C? . . . A reta ou AB é o suporte das semi-teras CA ou CB? . . . A poção de uma reta r, definidas por dois de seus pontos P e Q, é chamada segmento, e é representada por ou PQ? . . . Medir um segmento é compará-lo com outro tomado como unidade? . . . O número, resultante da medida de um segmento, é também chamado de distância entre os dois pontos? T. . . É comum dizer-se que o segmento PQ mede 3 cm? . . . isto significa que o resultado da medida é 3, adotando-se o centímetro como unidade? A P u | C u 1 cm | | u Q | | B r D m(PQ) = 3 (lê-se: a medida de PQ é igual a 3)

. . . É usual representar-se a medida do segmento de extremos P e Q. Simplesmente por PQ ao invés de m (PQ)? . . . Os segmentos da figura seguinte são chamados congruentes, porque apresentam a mesma medida (adotando-se a mesma unidade)? M | N | R | | | S | r MN ≡ RS (lê-se: MN é congruente a RS) . . . neste caso, usando a notação (representação) simplificada, podemos escrever - MN ≡ RS . . . os segmentos definidos na mesma reta (isto é, que têm na mesma reta suporte) são denominados colineares? (adotando-se a mesma unidade)? A | B | C | D | E | F | r Segmentos colineares: AB, CD e EF

. . . os segmentos da figura a seguir são consecutivos, porque, considerados dois a dois, só possuem um extremo em comum? N Q M P Segmentos consecutivos: MN ᵔ NP = (N) NP ᵔ PQ = (P) . . . O plano é, também, um conjunto infinito de pontos? . . . Na sua representação são usadas letras do alfabeto grego (α – alfa, β – beta, γ – gama, . . . )? . . . um plano contém uma infinidade de retas? . . . as retas que estão no mesmo plano são chamadas coplanares? r s t (α) Plano (α) r⊂α s⊂α t⊂α r, s e t São coplanares

. . . as retas coplanares que não tem ponto em comum são denominadas paralelas? . . . as retas concorrentes ou incidentes são coplanares e apresentam somente um ponto em comum? . . . duas retas representadas pelo mesmo conjunto de pontos são chamadas coincidentes (ou não-distintas)? r p s A (α) q U t Retas paralelas: r e s r⊂α s⊂α rᵔs = ø r // s Retas concorrentes: p e q { p ᵔ q = {A} Retas coincidentes: u e t { u ᵔ t = u ᵕ t . . . traçando uma reta, no chão de sua casa, e outra no teto, elas não se encontram, e, entretanto, pode não ser paralelas? Examine a figura seguinte

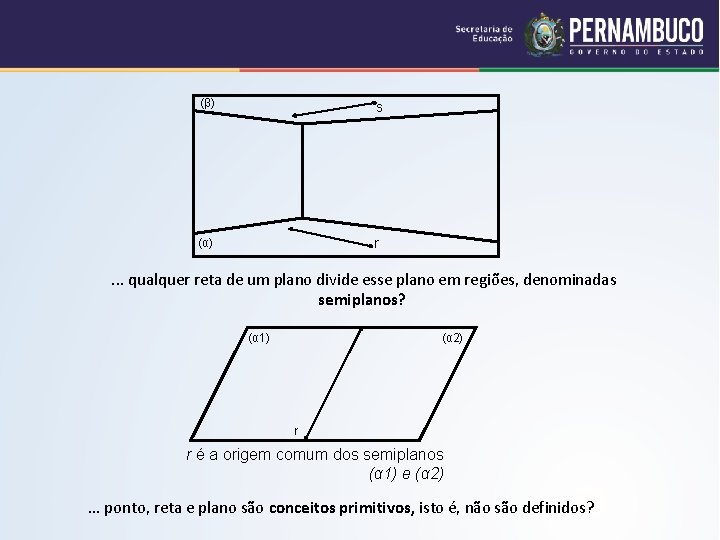
(β) s (α) r . . . qualquer reta de um plano divide esse plano em regiões, denominadas semiplanos? (α 1) (α 2) r r é a origem comum dos semiplanos (α 1) e (α 2) . . . ponto, reta e plano são conceitos primitivos, isto é, não são definidos?

. . . ponto, reta e plano são conceitos primitivos, isto é, não são definidos? N Q M P Segmentos consecutivos: MN ᵔ NP = (N) NP ᵔ PQ = (P) . . . O plano é, também, um conjunto infinito de pontos? . . . Na sua representação são usadas letras do alfabeto grego (α – alfa, β – beta, γ – gama, . . . )? . . . um plano contém uma infinidade de retas? . . . as retas que estão no mesmo plano são chamadas coplanares? r s t (α) Plano (α) r⊂α s⊂α t⊂α r, s e t São coplanares

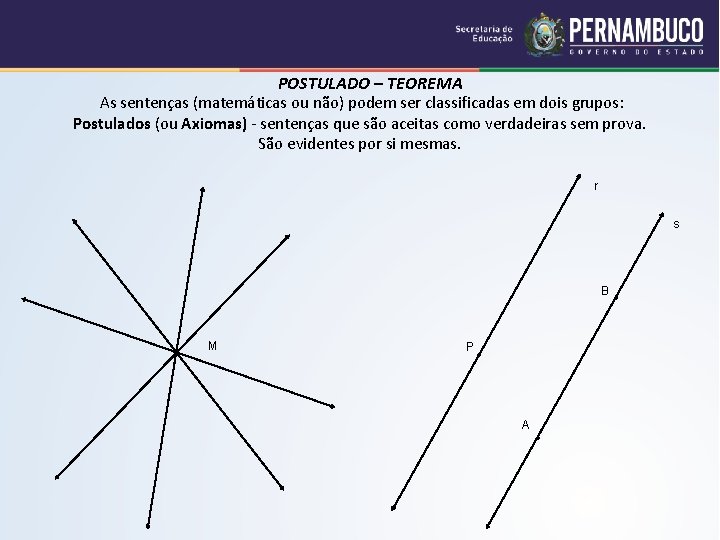
POSTULADO – TEOREMA As sentenças (matemáticas ou não) podem ser classificadas em dois grupos: Postulados (ou Axiomas) - sentenças que são aceitas como verdadeiras sem prova. São evidentes por si mesmas. r s B M P • A • •

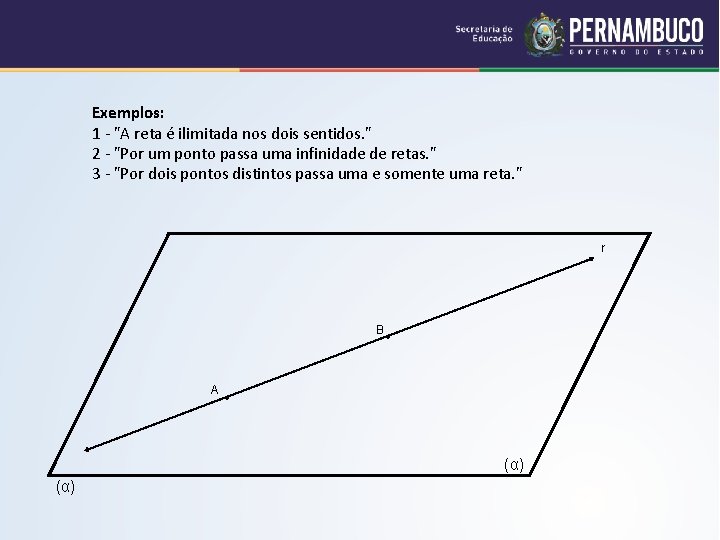
Exemplos: 1 - "A reta é ilimitada nos dois sentidos. " 2 - "Por um ponto passa uma infinidade de retas. " 3 - "Por dois pontos distintos passa uma e somente uma reta. " r B A • • (α)

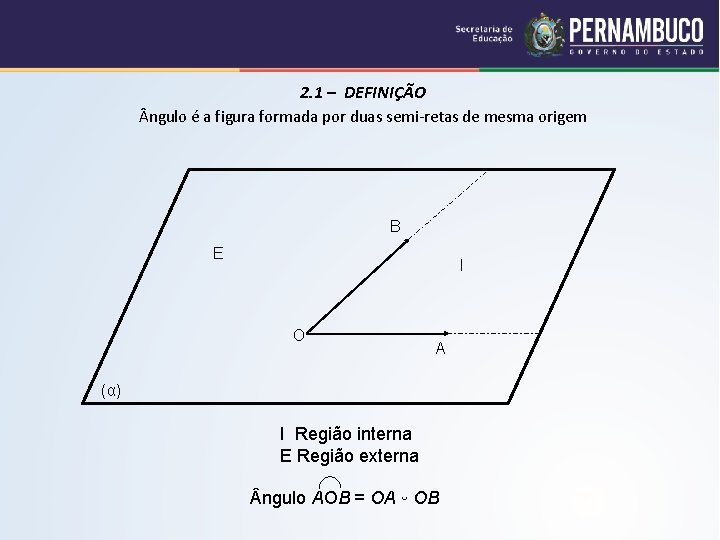
2. 1 – DEFINIÇÃO ngulo é a figura formada por duas semi-retas de mesma origem B E I O A (α) I Região interna E Região externa ngulo AOB = OA ᵕ OB

2. 2 – NGULOS CONGRUENTES São aqueles que podem coincidir por superposição C B D F A E ABC ≡ DEF (lê-se: o ângulo ABC é congruente ao ângulo DEF)

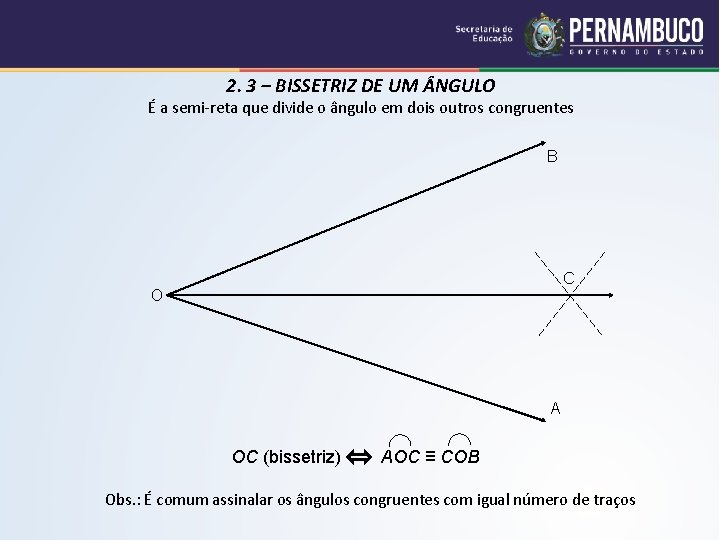
2. 3 – BISSETRIZ DE UM NGULO É a semi-reta que divide o ângulo em dois outros congruentes B C O A OC (bissetriz) AOC ≡ COB Obs. : É comum assinalar os ângulos congruentes com igual número de traços

2. 4 – RETAS PERPENDICULARES: NGULO RETO Duas retas são perpendiculares quando são concorrentes e formam quatro ângulos congruentes. Denomina-se ângulo reto a qualquer um desses ângulos. Representa-se por r ou ( ) Obs. : Se os ângulos não forem congruentes (DEB e DEO), as retas são oblíquas. BOD ≡ DOA ≡ AOC ≡ COB ≡ 1 r D A O E C CD AB (lê-se: CD é perpendicular a AB) DE AB (lê-se: DE é oblíqua a AB) B

2. 5 – MEDIDA DE NGULOS (Sistema sexagésima) Grau 0 1° = 1 r/90 Minuto ‘ 1’ = 1°/60 Segundo “ 1” = 1’/60

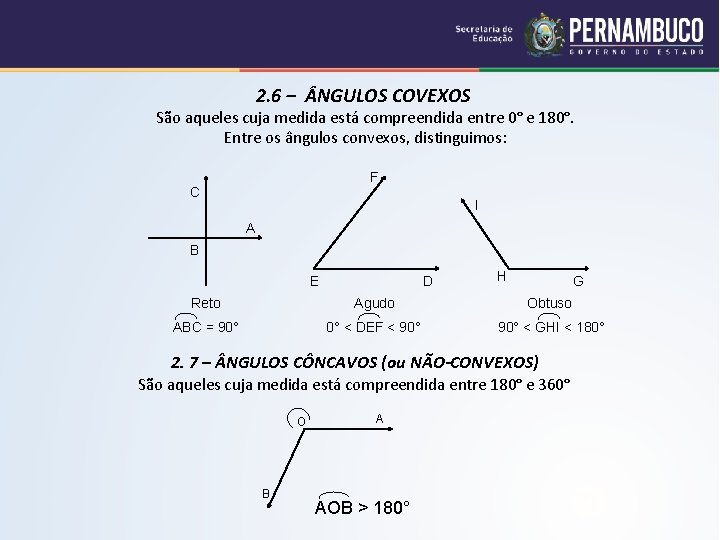
2. 6 – NGULOS COVEXOS São aqueles cuja medida está compreendida entre 0° e 180°. Entre os ângulos convexos, distinguimos: F C I A B E D H G Reto Agudo Obtuso ABC = 90° 0° < DEF < 90° < GHI < 180° 2. 7 – NGULOS CÔNCAVOS (ou NÃO-CONVEXOS) São aqueles cuja medida está compreendida entre 180° e 360° O B A AOB > 180°

2. 8 – NGULOS COMPLEMENTARES, SUPLEMENTARES REPLEMENTARES Dois ângulos são complementares quando a soma de suas medidas é igual a 90° (1 reto). Neste caso, cada um deles diz-se complemento do outro. Exemplo: O complemento de 28° é 62°, porque 28° + 62° = 90°. Dois ângulos são suplementares quando a soma de suas medidas é igual a 180° (2 retos). Dois ângulos são replementares quando a soma de suas medidas é igual a 360° (4 retos). Daí, representando a medida de um ângulo por x, teremos: Complemento 90° - x Suplemento 180° - x Replemento 360° - x

2. 9 – NGULOS ADJACENTES dois ângulos são adjacentes quando têm o mesmo vértice e um lado comum, compreendido entre os não-comuns C B 115° D 35° 30° A O AOB e BOC ; lado comum: OB AOC e BOD ; lado comum: OB AOC e COD ; lado comum: OC Da figura acima você conclui que: AOC + COD = 180° De um modo geral, podemos dizer: Teorema: “Dois ângulos adjacentes, que têm os lados não comuns em linha reta, são suplementares. ”

2. 10 - NGULOS OPOSTOS PELO VÉRTICE (O. P. V. ) Dois ângulos são opostos pelo vértice, quando o lado de um deles são as semi-retas opostas dos lados do outro B C d a O b c D A AOC e BOD AOD e BOC 2. 11 – TEOREMA "Dois ângulos opostos pelo vértice são congruentes. " Na figura acima temos: a = b ; c = d

2. 12 - EXERCÍCIOS RESOLVIDOS 1 – reduza à fração de grau: a) 20° 36 b) 45° 12' 60’ → 1° Solução: a) → x = 36/60 = Logo: 20° 36' = 20° + 0, 6° = 20, 6° 36’ → x Observação: 1° → 60’ Da proporcionalidade , concluímos que 0, 1° = 6’ 0, 1° → x b) pela observação, resulta: 12’ = 0, 2° assim: 45° 12’ = 45° + 0, 2° = 45, 2° 2 – Reduza à 4'48" a segundos. Solução: 1’ → 60” → x = 240” 4’ → x Logo: 4'48" = 240" + 48" = 248"

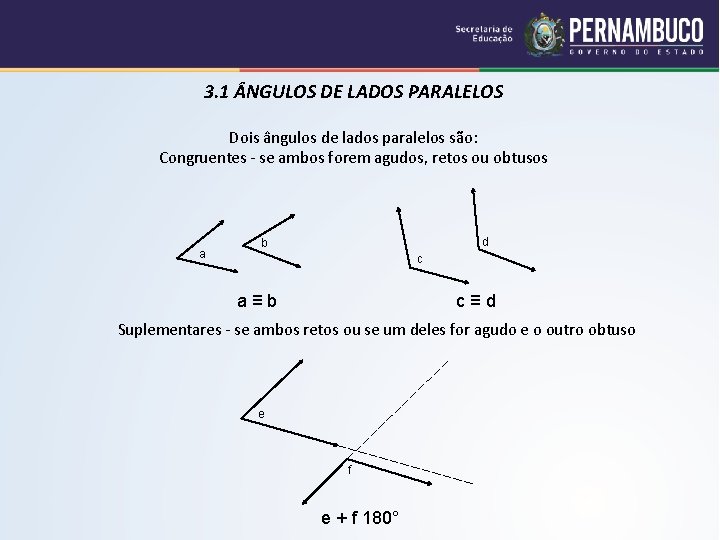
3. 1 NGULOS DE LADOS PARALELOS Dois ângulos de lados paralelos são: Congruentes - se ambos forem agudos, retos ou obtusos a d b c a≡b c≡d Suplementares - se ambos retos ou se um deles for agudo e o outro obtuso e f e + f 180°

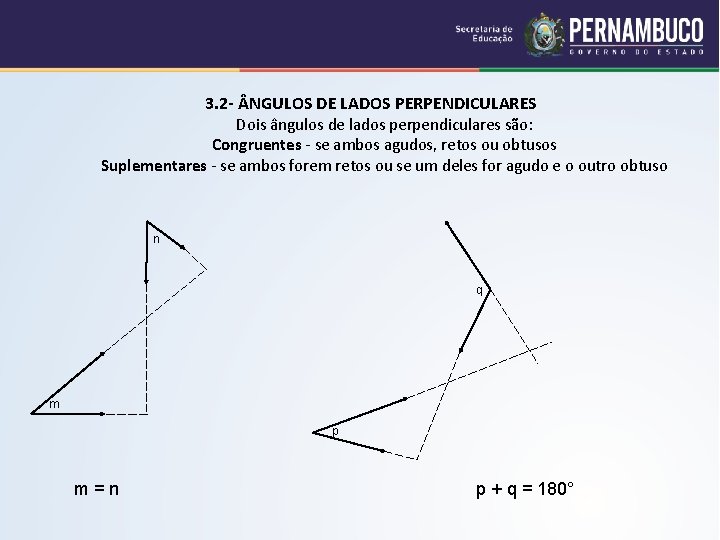
3. 2 - NGULOS DE LADOS PERPENDICULARES Dois ângulos de lados perpendiculares são: Congruentes - se ambos agudos, retos ou obtusos Suplementares - se ambos forem retos ou se um deles for agudo e o outro obtuso n q m p m=n p + q = 180°

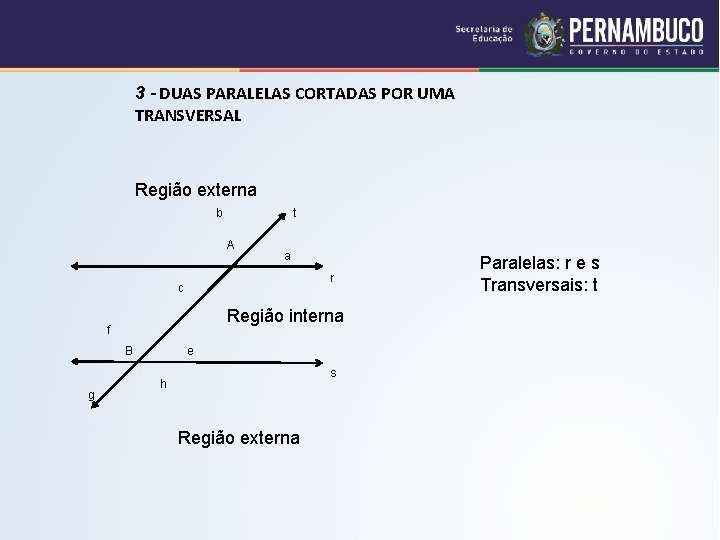
3 - DUAS PARALELAS CORTADAS POR UMA TRANSVERSAL Região externa b t A a r c Região interna f B g e s h Região externa Paralelas: r e s Transversais: t

Os pares de ângulos (um com vértice em A e outro em B) são definidos da seguinte forma: Do mesmo lado da transversal Ambos na região interna: Colaterais Internos (d; e) (c; f) Ambos na região externa: Colaterais Externos (a; h) (b; g) Uma na região interna e outro na externa: Correspondentes (a; e) (b; f) (d; h) (c; g) Em lados opostos da transversal Ambos na região interna: Alternos Internos (c; e) (d; f) Ambos na região externa: Alternos Externos (a; g) (b; h)

Conclusões: Do conhecimento dos ângulos opostos pelo vértice (2. 10 e 2. 11) e dos de lados paralelos (3. 1), resulta que, na fig. 22: a=c=e=g b = d =f = h Correspondentes Alternos internos Alternos externos Colaterais interno Colaterais externos Congruentes Suplementares