Matematiko klatno MATURSKI RAD NIKOLA FILPOVI Uvod OSCILATORNO

Matematičko klatno MATURSKI RAD NIKOLA FILPOVIĆ

Uvod OSCILATORNO KRETANJE MATEMATIČKO KLATNO – OSNOVNI POJMOVI

Oscilatorno kretanje Jedno od fundamentalnih vrsta kretanja u fizici Sila koja deluje na telo proporcionalna je otklonu od ravnotežnog položaja (restituciona sila) Karakteristična funkcija položaja tela od vremena je sinusna funkcija U realnosti, uvek postoji gubitak energije koji se manifestuje kao prigušenje oscilatornog kretanja

Matematičko klatno – osnovni pojmovi Sistem sačinjen od tanke neistegljive niti zanemarljive mase, okačene o oslonac, i tela zanemarljivih dimenzija okačenog o tu nit Oscilovanje pod dejstvom tangencijalne komponente težine tela

Prosto harmonijsko kretanje ANALITIČKO REŠENJE NUMERIČKO REŠENJE (OJLEROV I OJLER – KROMEROV METOD) LINEARNO I NELINEARNO REŠENJE

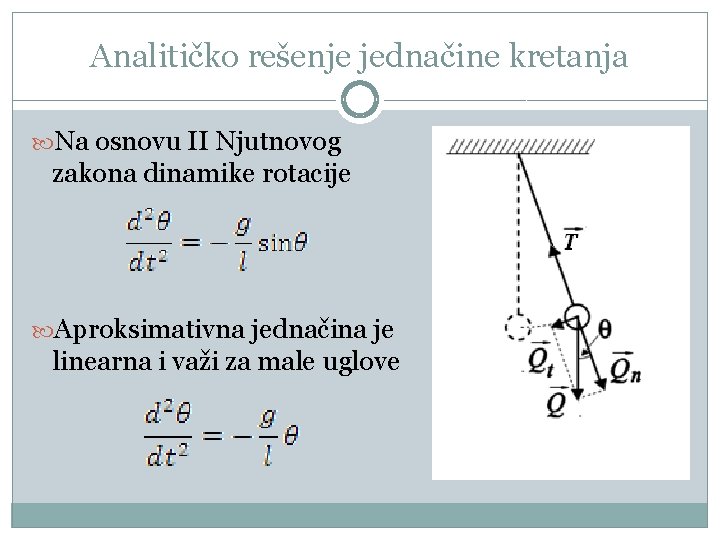
Analitičko rešenje jednačine kretanja Na osnovu II Njutnovog zakona dinamike rotacije Aproksimativna jednačina je linearna i važi za male uglove

Analitičko rešenje jednačine kretanja Rešenje diferencijalne jednačine kretanja ima oblik Početni ugao otklona i početna faza oscilovanja zavise od početnih uslova Kretanje ne zavisi od mase kuglice, i periodično će se ponavljati zauvek, jer nema trenja u posmatranom modelu

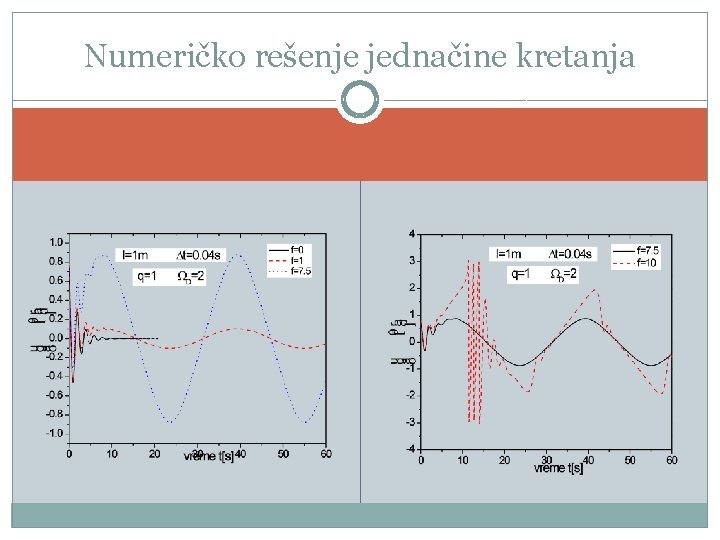
Numeričko rešenje jednačine kretanja Za numeričko rešavanje diferencijalnih jednačina obično se koristi Ojler – Kromerov metod Zavisnost ugla otklona od vremena se lako može isprogramirati, pri čemu se dobija određeni grafik

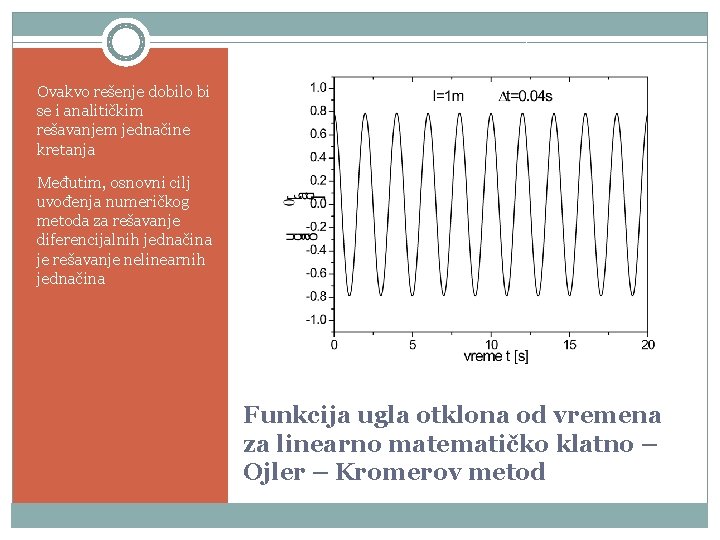
Ovakvo rešenje dobilo bi se i analitičkim rešavanjem jednačine kretanja Međutim, osnovni cilj uvođenja numeričkog metoda za rešavanje diferencijalnih jednačina je rešavanje nelinearnih jednačina Funkcija ugla otklona od vremena za linearno matematičko klatno – Ojler – Kromerov metod

Numeričko rešenje jednačine kretanja Ponovo Ojler – Kromerov metod, ovoga puta za nelinearno klatno Nema aproksimacije za male uglove

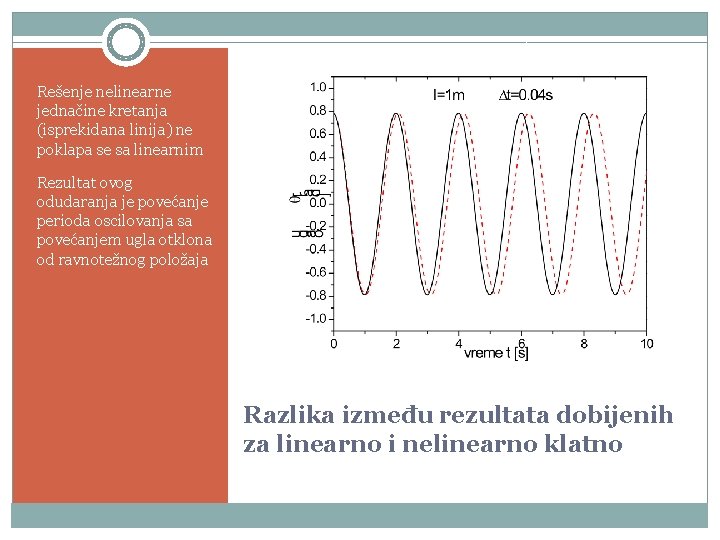
Rešenje nelinearne jednačine kretanja (isprekidana linija) ne poklapa se sa linearnim Rezultat ovog odudaranja je povećanje perioda oscilovanja sa povećanjem ugla otklona od ravnotežnog položaja Razlika između rezultata dobijenih za linearno i nelinearno klatno

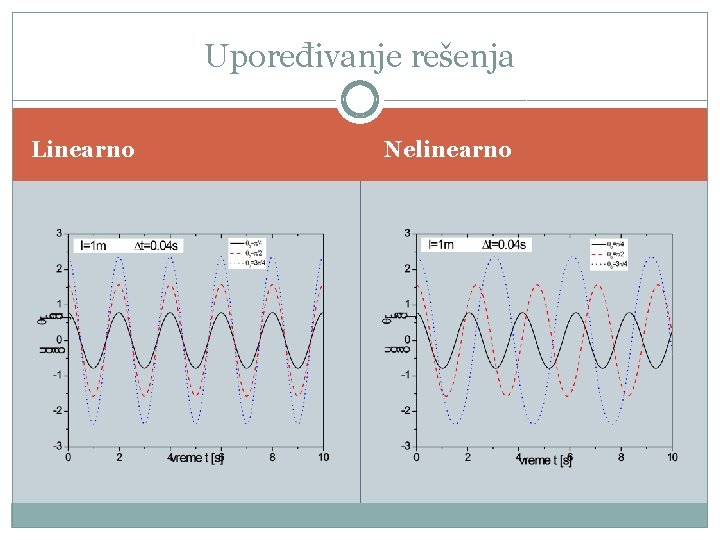
Upoređivanje rešenja Linearno Nelinearno

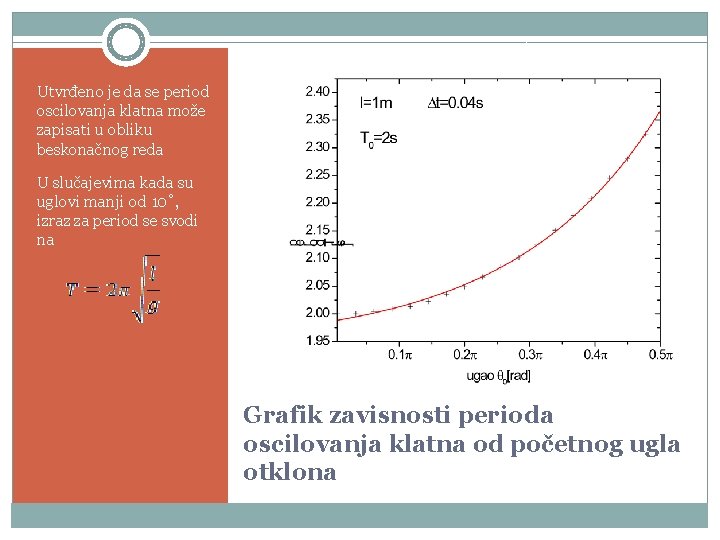
Utvrđeno je da se period oscilovanja klatna može zapisati u obliku beskonačnog reda U slučajevima kada su uglovi manji od 10˚, izraz za period se svodi na Grafik zavisnosti perioda oscilovanja klatna od početnog ugla otklona

Prigušeno oscilovanje ANALITIČKO REŠENJE NUMERIČKO REŠENJE (OJLER – KROMEROV METOD) LINEARNO I NELINEARNO REŠENJE

Analitičko rešenje jednačine kretanja Pojava sile trenja, koju klatno savladava, i na taj način gubi deo svoje energije (prigušenje) Jednačina kretanja je Aproksimativna jednačina je

Analitičko rešenje jednačine kretanja Više različitih slučajeva (rešenja), u zavisnosti od karakteristika prigušenja Karakteristična jednačina Natkritično rešenje (aperiodično) – sopstvene učestanosti realne i različite

Analitičko rešenje jednačine kretanja Kritično rešenje (aperiodično) – sopstvene učestanosti realne i jednake Podkritično rešenje (kvaziperiodično) – sopstvene učestanosti su konjugovano-kompleksne Periodično rešenje – sopstvene učestanosti imaginarne (prosto harmonijsko oscilovanje)

Numeričko rešenje (Ojler – Kromerov metod) Nelinearan sistem Linearan sistem

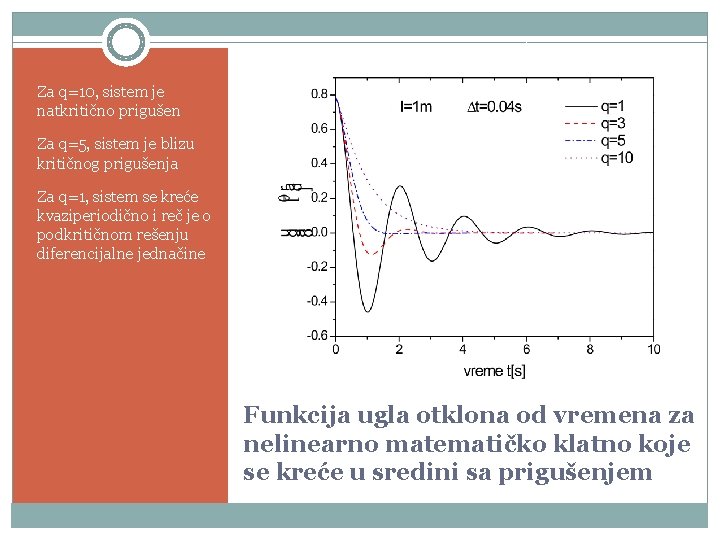
Za q=10, sistem je natkritično prigušen Za q=5, sistem je blizu kritičnog prigušenja Za q=1, sistem se kreće kvaziperiodično i reč je o podkritičnom rešenju diferencijalne jednačine Funkcija ugla otklona od vremena za nelinearno matematičko klatno koje se kreće u sredini sa prigušenjem

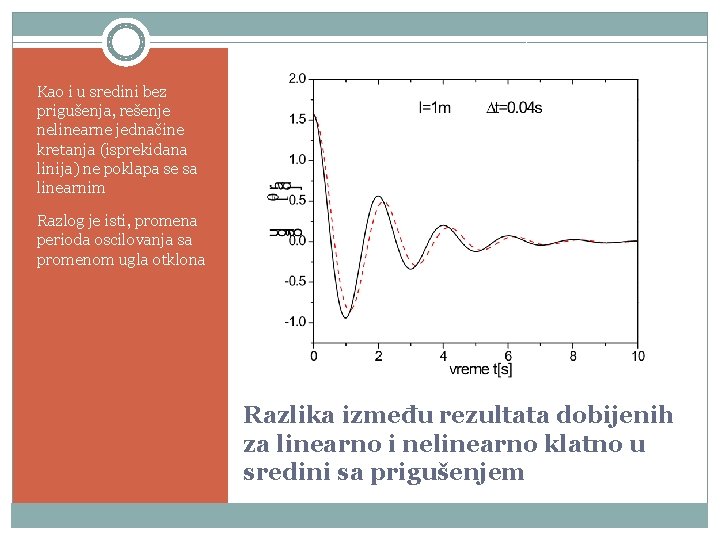
Kao i u sredini bez prigušenja, rešenje nelinearne jednačine kretanja (isprekidana linija) ne poklapa se sa linearnim Razlog je isti, promena perioda oscilovanja sa promenom ugla otklona Razlika između rezultata dobijenih za linearno i nelinearno klatno u sredini sa prigušenjem

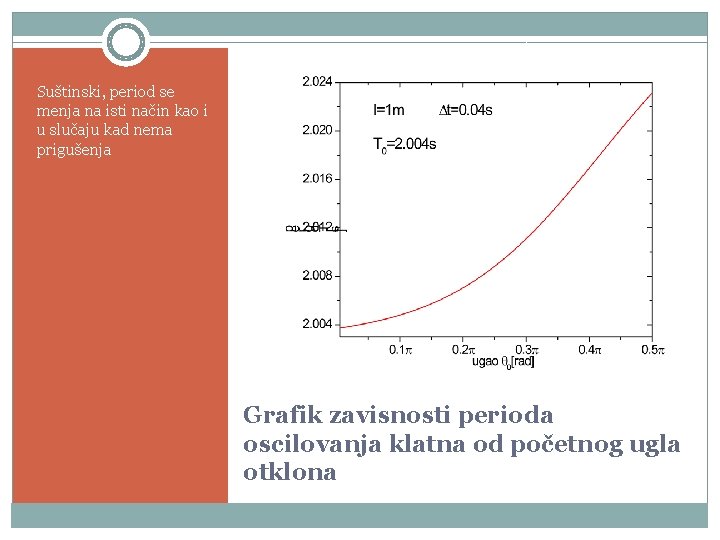
Suštinski, period se menja na isti način kao i u slučaju kad nema prigušenja Grafik zavisnosti perioda oscilovanja klatna od početnog ugla otklona

Upoređivanje rešenja Činjenica da period klatna nije konstantan u zavisnosti od amplitudnog ugla dokazuje nepouzdanost aproksimativnog rešenja Mogućnosti približnog rešenja jednačine kretanja klatna su na neki način ograničene Matematičko klatno je u realnosti nelinearan sistem, i upravo je ta činjenica presudna u određivanju njegovog ponašanja

Prinudno oscilovanje PRINUDNO OSCILOVANJE KOD LINEARNOG KLATNA PRINUDNO OSCILOVANJE KOD NELINEARNOG KLATNA

Analitičko rešenje jednačine kretanja Gubitak energije oscilatora, izazvan oscilovanjem u sredini koja prigušuje kretanje, se može nadoknaditi primenom spoljašnje sile koja bi vršila pozitivan rad na sistemu (prinudna sila) Prinudna sila može biti različite prirode (mehanička, električna, magnetna) Jednačina kretanja za linearno klatno

Analitičko rešenje jednačine kretanja Nakon dovoljno dugo vremena, energija, koju prilikom jedne pune oscilacije u sistem ubaci prinudna sila, postane jednaka energiji koja se izgubi usled prigušenja, te je rešenje jednačine kretanja Amplituda oscilovanja je data izrazom

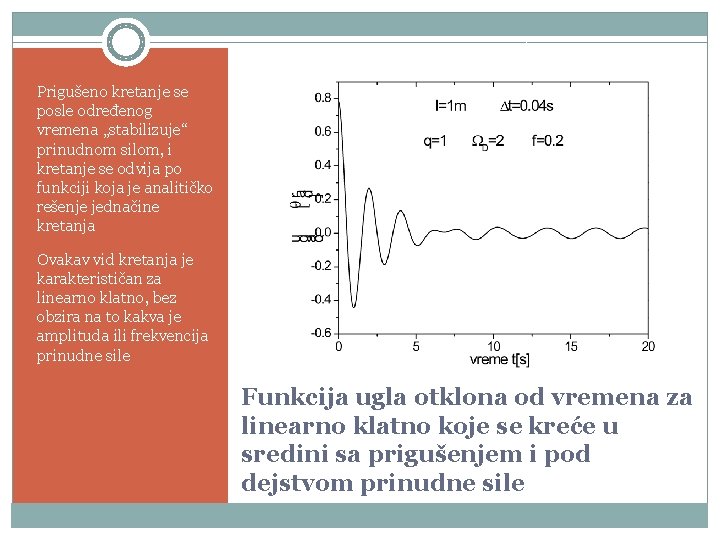
Prigušeno kretanje se posle određenog vremena „stabilizuje“ prinudnom silom, i kretanje se odvija po funkciji koja je analitičko rešenje jednačine kretanja Ovakav vid kretanja je karakterističan za linearno klatno, bez obzira na to kakva je amplituda ili frekvencija prinudne sile Funkcija ugla otklona od vremena za linearno klatno koje se kreće u sredini sa prigušenjem i pod dejstvom prinudne sile

Numeričko rešenje jednačine kretanja Kretanje nelinearnog klatna je i dalje periodično, ali se ne može opisati sinusnom ili kosinusnom funkcijom Najsloženiji oblik diferencijalne jednačine koji opisuje kretanje klatna dat je kao Ojler – Kromerov metod

Numeričko rešenje jednačine kretanja

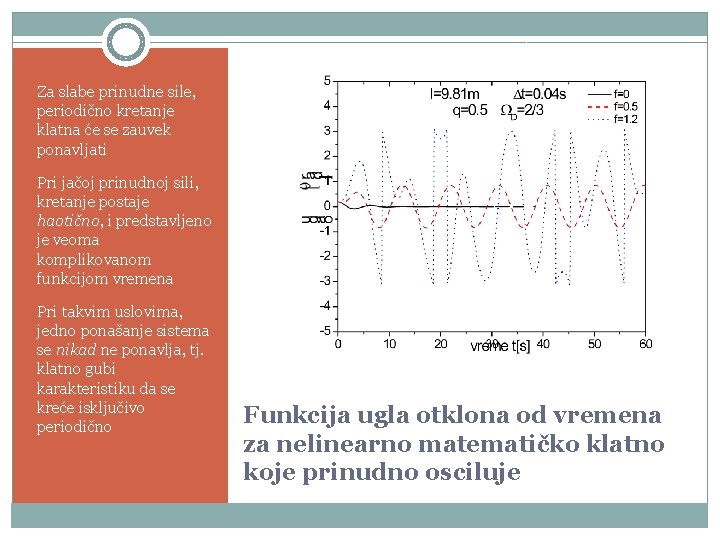
Za slabe prinudne sile, periodično kretanje klatna će se zauvek ponavljati Pri jačoj prinudnoj sili, kretanje postaje haotično, i predstavljeno je veoma komplikovanom funkcijom vremena Pri takvim uslovima, jedno ponašanje sistema se nikad ne ponavlja, tj. klatno gubi karakteristiku da se kreće isključivo periodično Funkcija ugla otklona od vremena za nelinearno matematičko klatno koje prinudno osciluje

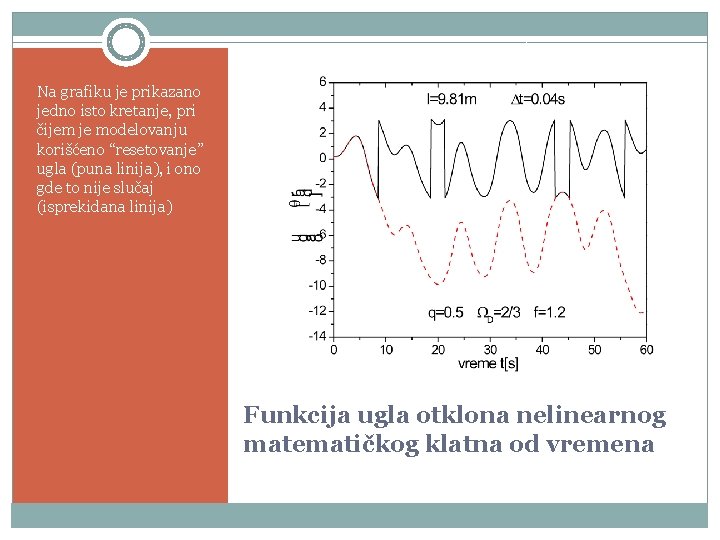
Na grafiku je prikazano jedno isto kretanje, pri čijem je modelovanju korišćeno “resetovanje” ugla (puna linija), i ono gde to nije slučaj (isprekidana linija) Funkcija ugla otklona nelinearnog matematičkog klatna od vremena

Zaključak RAZLIKE IZMEĐU LINEARNIH I NELINEARNIH SISTEMA OSNOVNI POJMOVI U TEORIJI HAOSA

Linearni i nelinearni sistemi Modelovanje kretanja klatna bilo bi prilično neinteresantno kada bi se posmatralo u svom najjednostavnijem obliku Podela na linearne i nelinearne sisteme Razlike Period oscilovanja Haotično kretanje pod dejstvom prinudne sile

Osnovni pojmovi teorije haosa U matematici, teorija haosa opisuje ponašanje određenih dinamičkih sistema, tj. onih čije stanje sistema evoluira u toku vremena Ponašanje haotičnih sistema izgleda slučajno, čak i ako su sistemi deterministički, što znači da im je dinamika potpuno određena početnim uslovima, bez slučajnih faktora (deterministički haos, haos) Posledica nelinearnosti sistema Ponašanje vremena i klime, rast populacije u ekologiji, mehanički i magnetno-mehanički procesi itd.

HVALA NA PAŽNJI!!!