Matematika Teknik 3 IT 041221 PD eksak variabel

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 Atau jika ruas ditukar Jika Artinya Bentuk ini disebut Persamaan Diferensial Eksak Syarat: Tunjukkan bahwa Syarat di atas harus dipenuhi Eksak

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Sebaliknya, Pertemuan 01 periksa apakah Persamaan Diferensial adalah eksak? Periksa apakah Syarat tidak terpenuhi, jadi PD di atas bukan eksak Penyelesaian PD Eksak 1. . 2. . 3. . 4. . Latihan PD Eksak

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 Penyelesaian PD Eksak 1. . 2. . 3. . 4. . ⇒ PD Eksak 1). 2) 3) 4) 5) Solusi =

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 Penyelesaian PD Eksak 1. . 2. . 3. . 4. . ⇒ PD Eksak 1). 2) 3) 4) 5) Solusi =

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 Penyelesaian PD Eksak 1. . 2. . 3. . 4. .

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 Persamaan Diferensial Variabel Terpisah (Variables Separable) disebut Persamaan Diferensial Variabel Terpisah, jika: dapat dinyatakan sebagai perkalian fungsi 1 variabel Dengan demikian, faktor integrasi-nya adalah: Tunjukkan bahwa Variabel Terpisah PD Periksa apakah memenuhi syarat ⇒ PD Variabel Terpisah Solusi: atau

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 faktor integrasi-nya adalah: Tunjukkan bahwa PD Variabel Terpisah Periksa apakah memenuhi syarat ⇒ PD Variabel Terpisah faktor integrasi-nya adalah: = Solusi:

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Solusi: Pertemuan 01 Lakukan teknik integral pecahan Latihan

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Soal: Pertemuan 01 Selesaikan PD berikut, apakah solusinya? apakah variabel terpisah?

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 Persamaan Diferensial Homogen disebut Persamaan Diferensial Homogen, jika: M(x, y) dan N(x, y) adalah fungsi-fungsi homogen dengan derajat (pangkat n dari λ) yang sama Fungsi f(x, y) disebut HOMOGEN jika f(λ x, λy)= λnf(x, y) Lakukan transformasi: y=vx sehingga dy=vdx+xdv Tunjukkan bahwa PD Homogen Periksa apakah memenuhi syarat M(λ x, λ y) = λ 2 y 2=λ 2 M(x, y) N(λx, λy)= λ 2(x 2 -λ 2 xy-y 2)=λ 2 N(x, y) ⇒ PD Homogen Solusi: i. f=

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 Persamaan Diferensial Homogen Solusi: i. f=

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 Persamaan Diferensial Homogen Solusi: F(x, y) = ∂F(x, y) /∂y

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 Persamaan Diferensial Homogen Solusi: F(x, y) = ∂F(x, y) /∂y

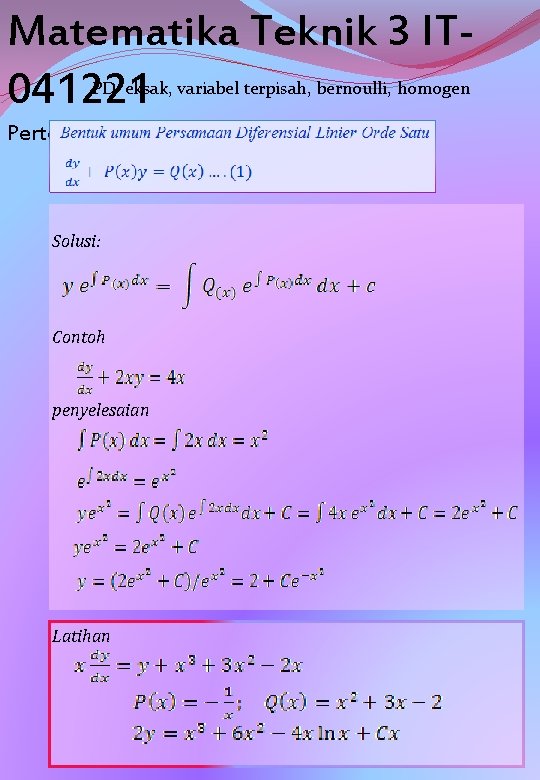
Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 Solusi: Contoh penyelesaian Latihan

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 Solusi: Contoh penyelesaian

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Persamaan Pertemuan 01 Diferensial eksak. SUDAH diperiksa bahwa Penyelesaian PD Non Eksak : Jika Contoh penyelesaian bukan

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Penyelesaian 01 PD Non Eksak : Pertemuan Jika Contoh penyelesaian

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Penyelesaian 01 PD Non Eksak : Pertemuan Jika Periksa Menjadi Penyelesaian PD Eksak 1. . 2. . 3. . 4. .

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Penyelesaian 01 PD Non Eksak : Pertemuan Penyelesaian PD Eksak 1. . 2. . 3. . 4. .

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Penyelesaian 01 PD Non Eksak : Pertemuan Penyelesaian PD Eksak 1. . 2. . 3. . 4. .

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen PD Non Eksak 01 : Pertemuan Latihan Penyelesaian PD Eksak 1. . 2. . 3. . 4. .

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen PD Non Eksak 01 : Pertemuan Latihan

Matematika Teknik 3 IT 041221 PD eksak, variabel terpisah, bernoulli, homogen Pertemuan 01 Sumber Frank Ayres, JR, Ph. D, Theory and Problems of Differential Equations, 1 st Edition, © Mc. Graw-Hill International Book Company, 1981