Matematika Elipsa Vukov materil slo projektu CZ 1

Matematika Elipsa

Výukový materiál Číslo projektu: CZ. 1. 07/1. 5. 00/34. 0608 Šablona: III/2 Inovace a zkvalitnění výuky prostřednictvím ICT Číslo materiálu: 06_02_32_INOVACE_10

ELIPSA Předmět: Matematika Ročník: 3. Jméno autora: Mgr. Hana Gaďurková Škola: SPŠ Hranice Anotace : obsahuje ukázkově řešené příklady a příklady k procvičení určování rovnic elipsy Klíčová slova: elipsa, ohnisko, osa, poloosa, středová rovnice, obecná rovnice Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Mgr. Hana Gaďurková Financováno z ESF a státního rozpočtu ČR.

ELIPSA Co to vlastně je ELIPSA? Elipsa je kuželosečka. Elipsa je množina všech bodů X v rovině, které mají od dvou bodů (ohnisek elipsy F 1, F 2) konstantní součet vzdáleností kde je délka hlavní osy elipsy.

Jak vypadá elipsa? obr. 1

S[m; n] A, B o 1 C, D o 2 F 1, F 2 X[x; y] střed elipsy hlavní vrcholy hlavní osa elipsy vedlejší vrcholy vedlejší osa elipsy ohniska elipsy libovolný bod elipsy délka hlavni osy délka vedlejší osy délka hlavní poloosy délka vedlejší poloosy excentricita (ohnisková vzdálenost, výstřednost)

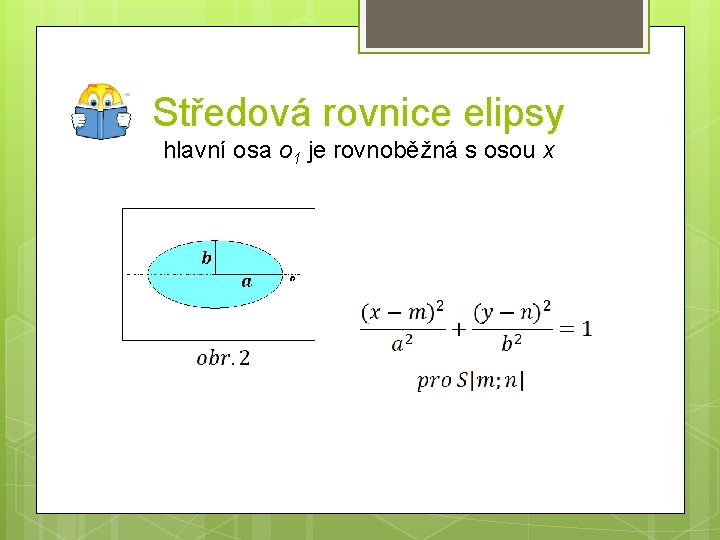
Středová rovnice elipsy hlavní osa o 1 je rovnoběžná s osou x

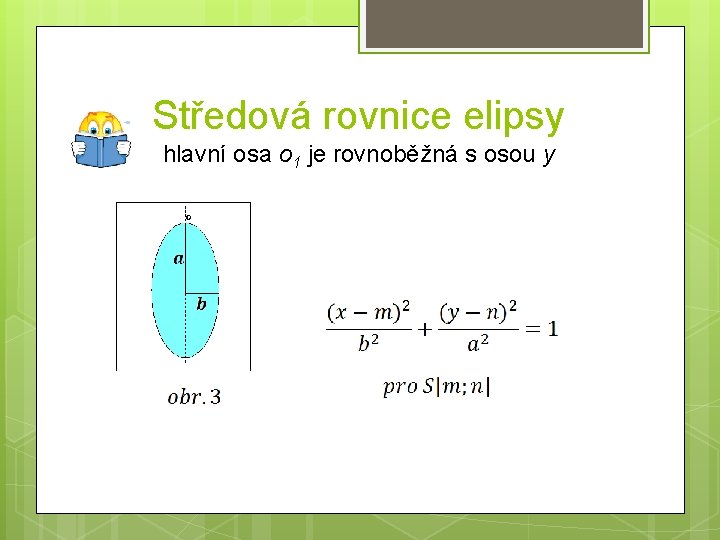
Středová rovnice elipsy hlavní osa o 1 je rovnoběžná s osou y

Příklad 1 Určete středovou a obecnou rovnici elipsy se středem S[-4; 3] a jejím bodem A[-1; 4], je–li .

Řešení příkladu 1 Středová rovnice má tvar Po dosazení souřadnic středu S, bodu A délky hlavní poloosy dostaneme: Středová rovnice má tedy tvar: a

Řešení příkladu 1 středovou rovnici upravíme na rovnici obecnou: …obecná rovnice elipsy

Příklad 2 Určete souřadnice středu, délky poloos, excentricitu a souřadnice ohnisek elipsy, která je daná obecnou rovnicí .

Řešení příkladu 2 Obecnou rovnic musíme převést do středového tvaru:

Řešení příkladu 2 Dostali jsme středovou rovnici: Odtud: střed S[2; -3], délky poloos Excentricitu vypočítáme ze vztahu: Souřadnice ohnisek nejlépe po náčrtku:

Úlohy k samostatnému řešení

1) Napište středovou a obecnou rovnici elipsy se středem S[0; 0], je – li dáno: 2) Určete středovou rovnici elipsy se středem S[0; 0] a jejím bodem M, je–li dáno: 3) Elipsa je určena hlavní osou AB, A[-4; 0], B[4; 0] a vedlejší osou CD, C[0; -1, 5], D[0; 1, 5]. Napište její obecnou rovnici a určete polohu ohnisek. 4) Stanovte souřadnice středu, délky poloos a excentricitu elipsy, je–li dána rovnicí:

Řešení příkladů: 1) 2) 3) 4)

Použité zdroje: obr. 1, obr. 2, obr. 3 archiv autora Části textu použity z učebnice: HUDCOVÁ, Milada; KUBIČÍKOVÁ, Libuše. Sbírka úloh z matematiky pro SOŠ, SOU a nástavbové studium. PRAHA: Prometheus, 2000, ISBN 80 -7196 -165 -5