Matematika 8 I dl sti kruhu Nejdve si

Matematika 8 – I. díl Části kruhu Nejdříve si zopakujeme základní vzorce: Obvod kruhu (délka kružnice) r o = 2 p r S Obsah kruhu S = p r 2 Tyto vzorce můžeme úspěšně použít i u příkladů, kde se vyskytují složitější obrazce složené z částí kruhu: Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

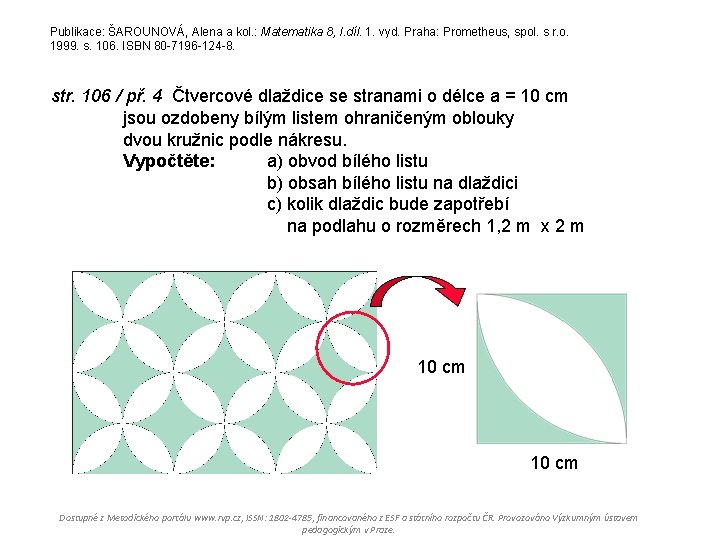
Publikace: ŠAROUNOVÁ, Alena a kol. : Matematika 8, I. díl. 1. vyd. Praha: Prometheus, spol. s r. o. 1999. s. 106. ISBN 80 -7196 -124 -8. str. 106 / př. 4 Čtvercové dlaždice se stranami o délce a = 10 cm jsou ozdobeny bílým listem ohraničeným oblouky dvou kružnic podle nákresu. Vypočtěte: a) obvod bílého listu b) obsah bílého listu na dlaždici c) kolik dlaždic bude zapotřebí na podlahu o rozměrech 1, 2 m x 2 m 10 cm Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

Navrhněte váš postup řešení Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

a) obvod bílého listu délka celé kružnice s poloměrem 10 cm: o = 2 p r o = 2. 3, 14. 10 r o = 62, 8 [cm] S Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

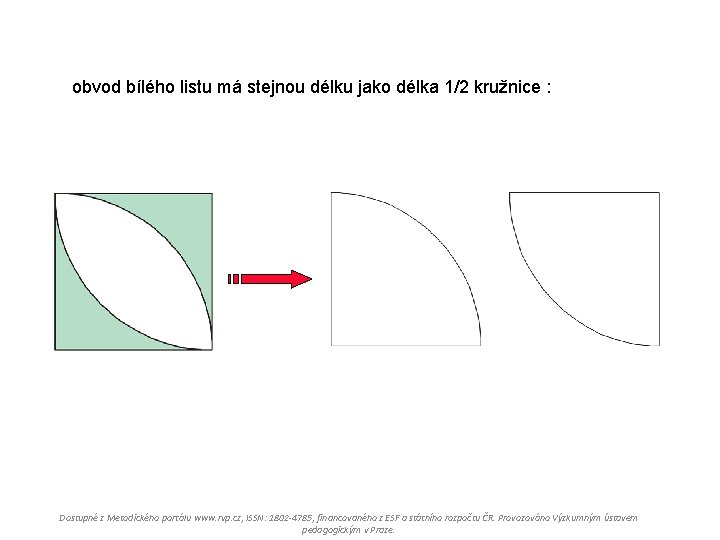
obvod bílého listu má stejnou délku jako délka 1/2 kružnice : Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

obvod bílého listu má stejnou délku jako délka 1/2 kružnice: o = 62, 8 : 2 = 31, 4 [cm] a) odpověď: Obvod bílého listu je přibližně 31, 4 cm. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

b) obsah bílého listu Obsah čtverce o straně 10 cm: S = a 2 S = 10. 10 S = 100 [cm 2] 10 cm Obsah jedné zeleně vybarvené části se rovná rozdílu obsahu čtverce a jedné čtvrtiny kruhu: SK = pr 2 SK = 3, 14. 102 1/4 SK = 314 [cm 2] ¼ SK = 314 : 4 = 78, 5 [cm 2] Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

Szelené části = 100 – 78, 5 = 21, 5 [cm 2] 1/4 Obsah bílého listu se rovná obsahu čtverce bez obsahu dvou těchto zelených částí: Slistu = 100 – 2. 21, 5 Slistu = 100 – 43 Slistu = 57 [cm 2] b) odpověď: Obsah bílého listu se rovná přibližně 57 cm 2. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

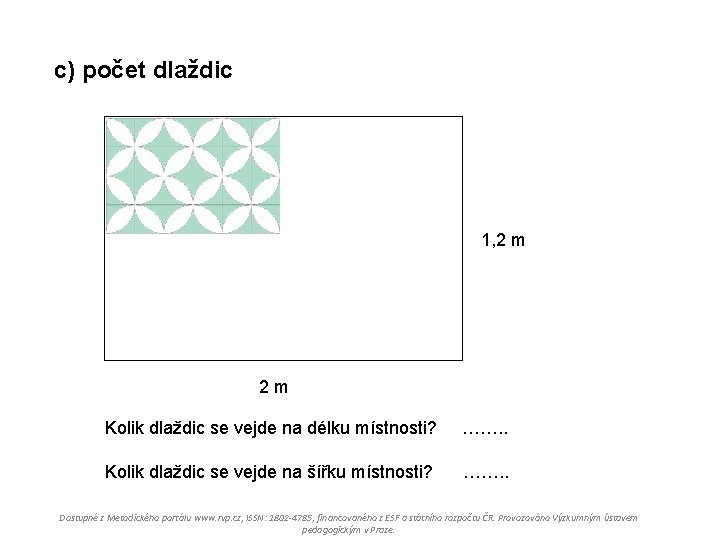
c) počet dlaždic 1, 2 m Kolik dlaždic se vejde na délku místnosti? ……. . Kolik dlaždic se vejde na šířku místnosti? ……. . Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

Kolik dlaždic se vejde na délku místnosti? 2 m = 200 cm Proč dělíme číslem 10? Počet dlaždic, které se vejdou na délku místnosti: 200 : 10 = 20 [ks] Kolik dlaždic se vejde na šířku místnosti? 1, 2 m = 120 cm Počet dlaždic, které se vejdou na šířku místnosti: 120 : 10 = 12 [ks] Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

Celkový počet dlaždic 20 x 12 = 240 [ks] Celkem je zapotřebí 240 kusů dlaždic. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.