Matematik dersi EMBER 7 snf ember Bildiklerimiz bir

Matematik dersi ÇEMBER 7. sınıf

Çember

Bildiklerimiz bir çemberin alanı ise, bilmediklerimiz de bir çemberin çevresi gibidir.

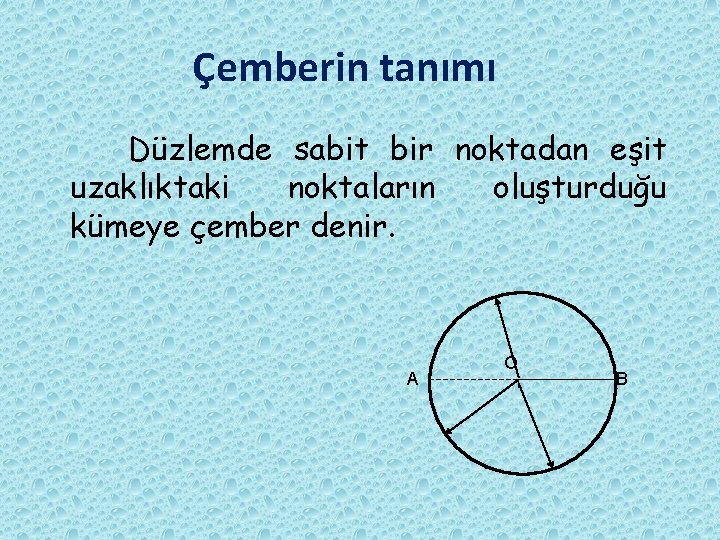
Çemberin tanımı Düzlemde sabit bir noktadan eşit uzaklıktaki noktaların oluşturduğu kümeye çember denir. A O B

ÇEMBERİN TARİHİ Geçmişten günümüze kadar ki insanoğlu bu şekli gökyüzündeki Güneş ve Ayda görüyordu. Fakat bir türlü anlamlandıramıyordu. Derken bir gün elindeki sopa ile, kum gibi düzgün yüzeylere daire çizdi. Sonra düşündü; bazı daireler küçük, bazıları ise büyüktü. Görüyordu ki (sezinliyordu ki), dairenin bir ucundan öteki ucuna olan uzaklığı (çapı), büyürse, çevresi de o kadar büyüyordu. Dairenin; çevresinin uzunluğu ile çapının uzunluğu orantılıydı. Çevrenin çapa oranı, daireden daireye değişmiyor, sabit kalıyordu. . Demek ki; bugünkü gösterim şekliyle, bu sabit orana ‘’Çevre/Çap = pi sabiti’’ diyebiliriz.

• Bu sabiti 16. yüzyılda isviçrede yaşayan LEONERD EULER pi sabitini bulmuştur. Bu çerçevede Çember ile pi sayısının bulunuşunu bağdaştırabiliriz.

• Genellikle bilinen en basit pi sayısı pek fazla bir şey ifade etmese de yaygınca kullanılır ve bu bakımdan anlamlıdır. Bu sayı aslında bir orandır ve dairenin çevresinin çapına bölümünden elde edilir. Bu oran 3, 14 olarak bilinir. İlginç olan ise insanoğlu çember ile doğada iç içeyken daha bunun farkında değildi. Ta ki çemberin varlığı bulununcaya kadar.

TEKERLEĞİN BULUNUŞU • Tekerleği kimlerin bulduğu tam olarak bilinmiyor. Ama tekerlek düşüncesi, hareket ettirilmek istenen ağır cisimlerin, örneğin teknelerin, altlarına kütüklerin dizilmesi halinde yuvarlandığı gözlendikten sonra ortaya çıkmış olabilir. • Bugüne kadar gerçekleştirilen en önemli buluş olarak kabul edilir. Eğer tekerlek olmasaydı, ağır eşya ve yükler insan ya da hayvan gücüyle taşınacak, bu da dev boyutlarda enerji harcanmasına neden olacaktı; yani tekerlek insanlığa çok önemli bir enerji tasarrufu sağlama olanağı yaratmıştır. Tekerlekli taşıtlar ulaşımı hızlandırmış, kolaylaştırmış ve insanların ürünlerini değiş tokuş edebilmelerine olanak vermiştir.

ÇEMBERİN GÜNLÜK HAYATTAKİ KULLANIMI Çemberin Kullanıldığı dallar Matematik, Geometri, Fizik, Mühendislik , Astronomidir.

Çember bilim dalları dışında günlük hayatımızda bir çok alanda kullanılır. . Evde, okulda, sporda, sanatta birçok iş alanında çemberin kullanıldığını görmek mümkündür.

Çember şeklinde ayakkabılık tasarımı • Şekilde görüldüğü gibi çember şekli günlük hayatımızda farklı kullanımlar ile karşımıza çıkmaktadır. Bunlarda n biride tekerlek şeklindeki ayakkabılıktır.

TEKNOLOJİ VE SPORDA KULLANIM ALANLARI

TABİATTA VE MİMARİDE ÇEMBER ÖRNEKLERİ

Amfi tiyatro • Tam çember ya da yumurta biçiminde bir sahne düzlüğünün çevresinde oturma yerlerinin basamaklar halinde yükseldiği bir açık hava tiyatro yapısıdır.

• İlk başta, dramatik gösterileri değil, gladyatör dövüşlerini, vahşi hayvan gösterilerini izlemek için yapılmış olan Amfitiyatrolar'ın ilki, Julius Ceasar'ın İ. Ö. 46 yılında yaptırdığı, en ünlüsü de Roma' daki Colosseum' dur. Amfi tiyatro yapıları, bir izleyici yeri (theatron), koronun şarkı söylediği çember biçimli bir orta olan (orkhestra) ile oyuncu yerini (skene) kapsıyordu.

1995’te İngiltere-Wiltshire ‘de ortaya çıkan ilginç bir ekin çemberi.

Stonehenge • İngiltere'deki Salisbury Düzlüğü'nde yontulmuş ve daha sonra da düzgünleştirilmiş mavi taşlardan oluşan bir çemberdir.

• Mavi taşlar bugün Stonehenge'in bulunduğu yere 240 kilometre ötedeki Güney Galler’in Preseli bölgesinden getirilmiş ve her dik konumdaki iki taşın üzerine lento ismi verilen bir kiriş taşı koyularak bir çember oluşturacak şekilde yerleştirilmişlerdir. Bu şekilde yerleştirilen ve çemberi oluşturan 30 taştan bugün 17 tanesi ayaktadır

Spiral Seyir Noktası • İsviçreli mimarlar HHF, Meksika’nın Guadalajara yakınlarındaki hac güzergahı üzerinde, spiral bir seyir noktası tasarladı. • .

Sümela manastırın da çember örnekleri

• ÇEMBERLİ TAŞ CAMİİ 1496 DA YAPILDI

Selimiye camiinde çember kullanımı

Selimiye camiinin çemberle çizilmiş projesi

YORUMSUZ

ÇEMBER a)Çember ve Elemanları Düzlemde sabit bir noktadan eşit uzaklıktaki noktaların oluşturduğu kümeye çember denir. A çap O yarıçap merkez Yukarıdaki çemberde; O noktasın, çemberin merkezi; [OB] doğru parçasına, çemberin yarı çapı, merkezden geçen [AB] na da çemberin çapı nedir. Yarı çapın uzunluğu r veya R ile gösterilir. l OB l= r veya l OA l= R dır. Çap, yarıçapın iki katı uzunluktadır. l AB l= 2 R Bir çember, merkezi ve yarıçap uzunluğu ile belirtilebilir. B

ÖRNEK O merkezli ve r yarıçaplı çember Ç(o, r) , A merkezli ve 5 cm çaplı çember Ç(A, 5 cm) biçiminde belirtilir. Ç(M, 7 cm) verilirse, yarıçap uzunluğu 7 cm olan M merkezli çember anlaşılır. b) Çemberin Düzlemden Ayırdığı Bölgeler B Yandaki şekilde görüldüğü gibi; bir çember, bulunduğu düzlemi iki bölgeye ayırır. Bunların birisi çemberin iç bölgesi diğeri de çemberin dış bölgesidir. Şekil incelenirse; A, B, C noktalarının O merkezine uzaklıkları farklıdır. çember C A içbölge p Dış bölge Bu noktaların bulundukları yere göre merkeze uzaklıklarının r yarıçapı ile karşılaştırılması şöyledir;

1) A noktası çember üzerindedir. Çemberin elemanı olan her bir noktanın çemberin merkezine olan uzaklığı, yarıçapının uzunluğuna eşittir. Yani, l OA l = r dır. l OA l = r bağıntısını sağlayan a gibi noktalar, çemberi oluşturur. 2) C noktası, çemberin iç bölgesindedir. iç bölgenin elemanı olan her bir noktanın çemberin merkezine olan uzaklığı, yarıçapının uzunluğundan küçüktür. l OC l < r bağıntısını sağlayan c gibi noktalar, iç bölgeyi oluşturur. 3) B noktası, çemberin dış bölgesindedir. dış bölgenin elemanı olan her bir noktanın çemberin merkezine olan uzaklığı, yarıçapının uzunluğundan büyüktür. l OB l > r bağıntısını sağlayan B gibi notalar, çemberin dış bölgesini oluşturur.

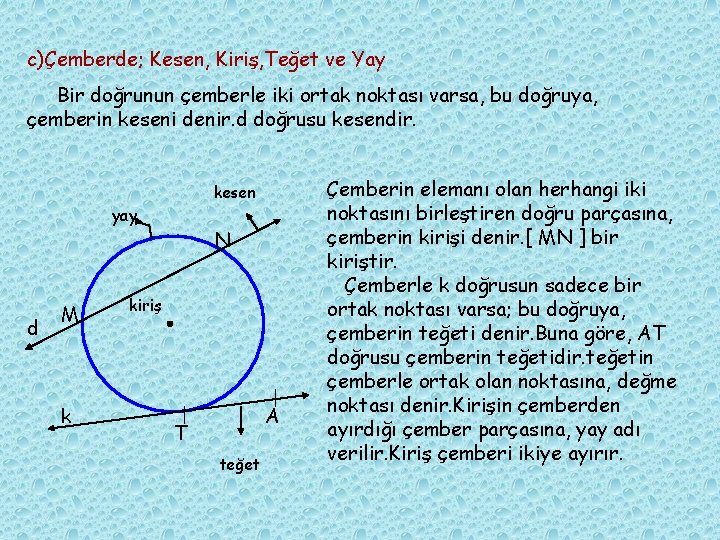
c)Çemberde; Kesen, Kiriş, Teğet ve Yay Bir doğrunun çemberle iki ortak noktası varsa, bu doğruya, çemberin keseni denir. d doğrusu kesendir. kesen yay d M k N kiriş A T teğet Çemberin elemanı olan herhangi iki noktasını birleştiren doğru parçasına, çemberin kirişi denir. [ MN ] bir kiriştir. Çemberle k doğrusun sadece bir ortak noktası varsa; bu doğruya, çemberin teğeti denir. Buna göre, AT doğrusu çemberin teğetidir. teğetin çemberle ortak olan noktasına, değme noktası denir. Kirişin çemberden ayırdığı çember parçasına, yay adı verilir. Kiriş çemberi ikiye ayırır.

Yemeklerde çemberin kullanımı

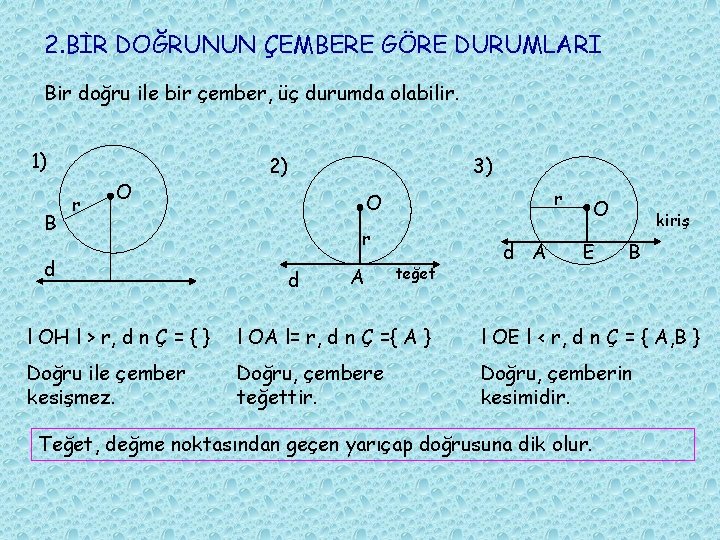
2. BİR DOĞRUNUN ÇEMBERE GÖRE DURUMLARI Bir doğru ile bir çember, üç durumda olabilir. 1) B r O d 2) 3) r O r d A teğet d A O E kiriş B l OH l > r, d n Ç = { } l OA l= r, d n Ç ={ A } l OE l < r, d n Ç = { A, B } Doğru ile çember kesişmez. Doğru, çembere teğettir. Doğru, çemberin kesimidir. Teğet, değme noktasından geçen yarıçap doğrusuna dik olur.

Kirişin Özellikleri 1. AB kirişinin orta noktası H dır. Çemberin merkeziyle H Noktasından geçen doğru d doğrusudur. l OA l = l OB l olduğundan, OAB üçgeni ikizkenar üçgendir. [OH] da bu ikizkenar üçgenin tabana ait kenar ortayıdır. Çemberde kirişin orta noktasının merkeze birleştiren doğru , kirişe diktir. Kirişin orta noktası merkezden geçer. d diktir [AB] olur. d F O A E H 2. Bir çemberde, eş kirişler merkezden eşit uzaklıkta dır. Merkezden eşit uzaklıktaki kirişlerin uzunlukları birbirine eşittir. F E O D A E B B

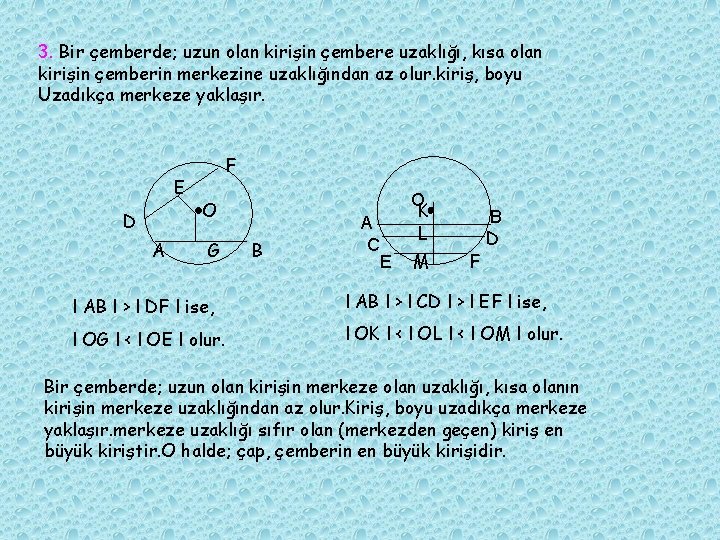
3. Bir çemberde; uzun olan kirişin çembere uzaklığı, kısa olan kirişin çemberin merkezine uzaklığından az olur. kiriş, boyu Uzadıkça merkeze yaklaşır. E D A F O G B A C E O K L M F B D l AB l > l DF l ise, l AB l > l CD l > l EF l ise, l OG l < l OE l olur. l OK l < l OL l < l OM l olur. Bir çemberde; uzun olan kirişin merkeze olan uzaklığı, kısa olanın kirişin merkeze uzaklığından az olur. Kiriş, boyu uzadıkça merkeze yaklaşır. merkeze uzaklığı sıfır olan (merkezden geçen) kiriş en büyük kiriştir. O halde; çap, çemberin en büyük kirişidir.

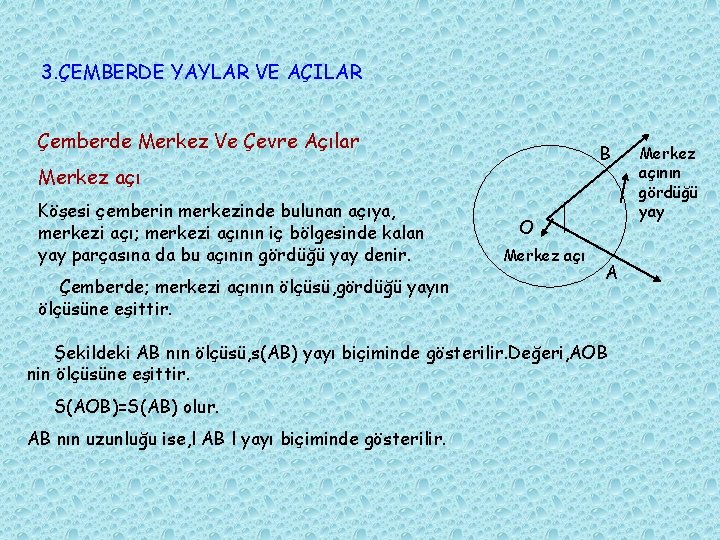
3. ÇEMBERDE YAYLAR VE AÇILAR Çemberde Merkez Ve Çevre Açılar B Merkez açı Köşesi çemberin merkezinde bulunan açıya, merkezi açı; merkezi açının iç bölgesinde kalan yay parçasına da bu açının gördüğü yay denir. Çemberde; merkezi açının ölçüsü, gördüğü yayın ölçüsüne eşittir. O Merkez açı A Şekildeki AB nın ölçüsü, s(AB) yayı biçiminde gösterilir. Değeri, AOB nin ölçüsüne eşittir. S(AOB)=S(AB) olur. AB nın uzunluğu ise, l AB l yayı biçiminde gösterilir. Merkez açının gördüğü yay

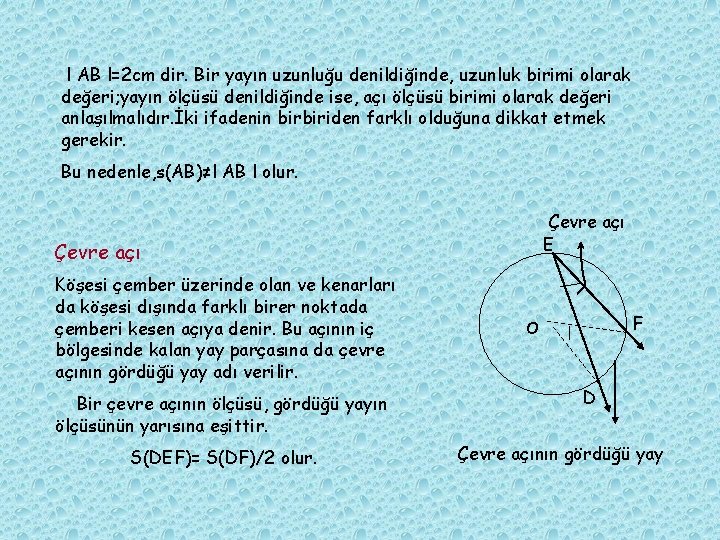
l AB l=2 cm dir. Bir yayın uzunluğu denildiğinde, uzunluk birimi olarak değeri; yayın ölçüsü denildiğinde ise, açı ölçüsü birimi olarak değeri anlaşılmalıdır. İki ifadenin birbiriden farklı olduğuna dikkat etmek gerekir. Bu nedenle, s(AB)≠l AB l olur. Çevre açı E Çevre açı Köşesi çember üzerinde olan ve kenarları da köşesi dışında farklı birer noktada çemberi kesen açıya denir. Bu açının iç bölgesinde kalan yay parçasına da çevre açının gördüğü yay adı verilir. Bir çevre açının ölçüsü, gördüğü yayın ölçüsünün yarısına eşittir. S(DEF)= S(DF)/2 olur. F O D Çevre açının gördüğü yay

Merkez açı ve çevre açının özellikleri 1. Bir çemberde; uzun olan yayı gören merkez açının ölçüsü, kısa yayı görenin ölçüsünden daha büyüktür. 2. Bir çemberde, eş yayları gören merkez açıların ölçüleri eşittir. 3. Bir çemberde, aynı veya eş yayları gören çevre açıların ölçüleri birbirine eşittir. 4. Bir çemberde çapı gören çevre açısının ölçüsü 90 derece dir. 5. Bir çemberde; aynı yayı gören çevre açının ölçüsü, merkez açının ölçüsünün yarısına eşittir.

ALIŞTIRMALAR

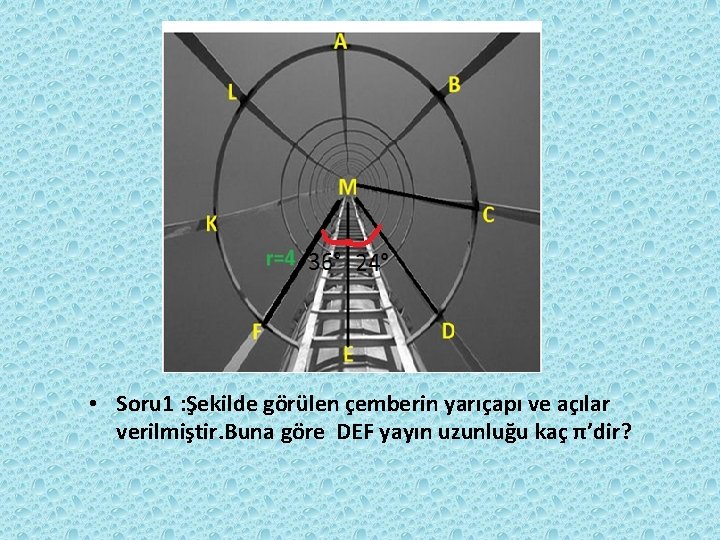
“ • Soru 1 : Şekilde görülen çemberin yarıçapı ve açılar verilmiştir. Buna göre DEF yayın uzunluğu kaç π’dir?

• Soru 2 : Yandaki saat 12 eşit parçaya bölünmüştür. x+y ölçüsünün toplamı kaçtır?

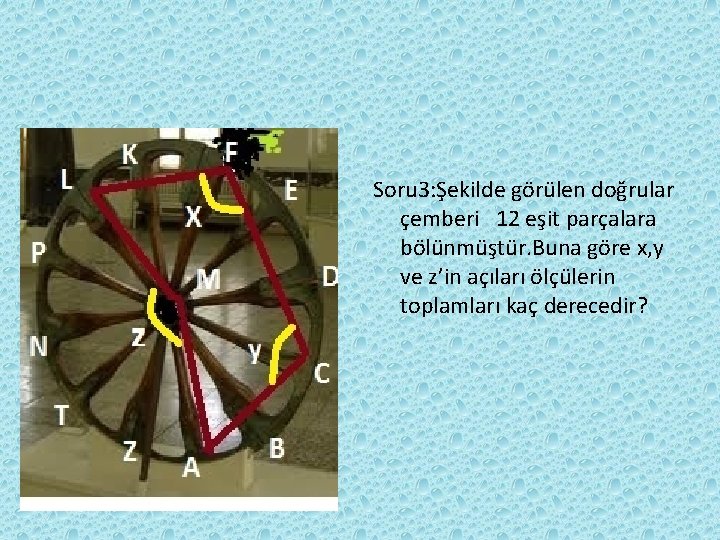
Soru 3: Şekilde görülen doğrular çemberi 12 eşit parçalara bölünmüştür. Buna göre x, y ve z’in açıları ölçülerin toplamları kaç derecedir?

• SORU 4: Lambaların arasındaki mesafeler eşittir. Buna göre A ile B noktalarına bakan merkez açının derecesi ile C ile E noktalarına bakan merkez açıların oranları kaçtır?

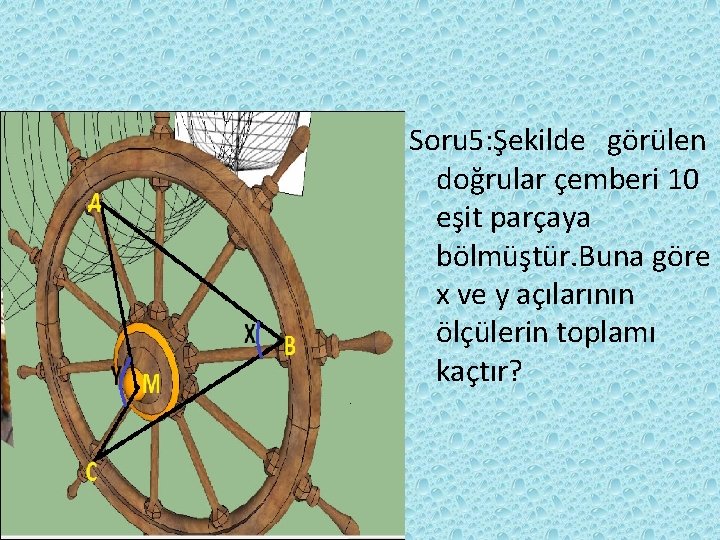
Soru 5: Şekilde görülen doğrular çemberi 10 eşit parçaya bölmüştür. Buna göre x ve y açılarının ölçülerin toplamı kaçtır?

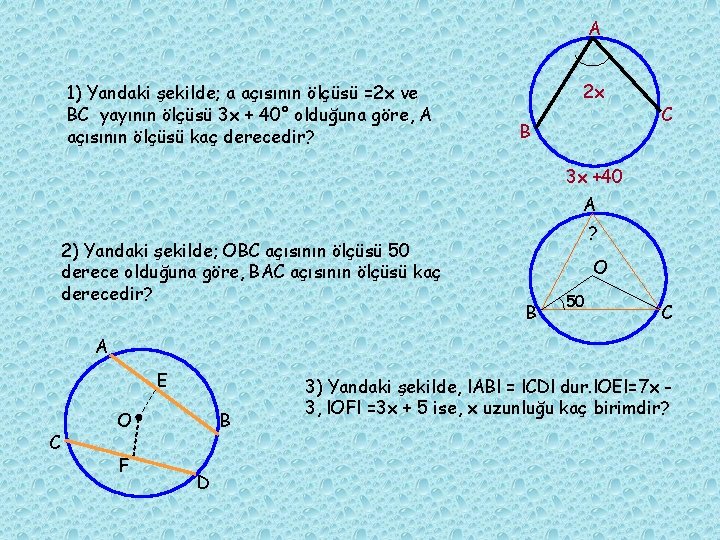
A 1) Yandaki şekilde; a açısının ölçüsü =2 x ve BC yayının ölçüsü 3 x + 40° olduğuna göre, A açısının ölçüsü kaç derecedir? 2 x B C 3 x +40 A 2) Yandaki şekilde; OBC açısının ölçüsü 50 derece olduğuna göre, BAC açısının ölçüsü kaç derecedir? ? O B 50 C A E C O F B D 3) Yandaki şekilde, l. ABl = l. CDl dur. l. OEl=7 x 3, l. OFl =3 x + 5 ise, x uzunluğu kaç birimdir?

HAZIRLAYANLAR İBRAHİM ERGÜN