MATEMATICA PER LECONOMIA e METODI QUANTITATIVI PER LA

MATEMATICA PER L’ECONOMIA e METODI QUANTITATIVI PER LA FINANZA a. a. 2010 -2011 (parte I: 4 cfu) • Orari di lezione: lunedì 15, 45 – 17, 15 aula D martedì 10, 15 – 11, 45 aula D mercoledì 14, 00 – 15, 30 aula 7 • Orario ricevimento: martedì 12, 00 – 13, 00

NUMERI COMPLESSI E DINTORNI

NUMERI REALI • L’insieme dei numeri reali è chiuso rispetto alle operazioni algebriche di +, -, *, : Questo significa che la somma, la differenza, il prodotto e il quoziente di 2 numeri reali è un numero reale. Non vale il viceversa! 3

NUMERI COMPLESSI • Sia , x non può essere un numero reale perché il quadrato di un numero reale non può essere uguale ad un numero reale negativo. • Si definisce unità immaginaria il numero i il cui quadrato è uguale a – 1: 4

NUMERI COMPLESSI • Un numero non reale (complesso) z può essere scritto nel seguente modo: • L’insieme dei numeri complessi viene indicato con C e risulta chiuso rispetto alle operazioni algebriche di somma, differenza, prodotto e divisione. 5

NUMERI COMPLESSI • Siano dati due numeri complessi • SOMMA: • DIFFERENZA: • PRODOTTO: 6

NUMERI COMPLESSI Si definisce numero complesso coniugato del numero complesso , il numero: • Il prodotto tra il numero complesso v e il suo complesso coniugato è dato dal numero reale (chiamato modulo di v): 7

NUMERI COMPLESSI • QUOZIENTE: 8

COORDINATE POLARI • P ha coordinate cartesiane (1, 1) Le coordinate polari di P sono: Nell’esempio: 9

COORDINATE POLARI • Esiste la seguente relazione tra le coordinate polari e cartesiane di un punto: • si osservi che: 10

COORDINATE POLARI E NUMERI COMPLESSI • Un numero complesso può essere rappresentato geometricamente dal punto, nel piano cartesiano, che ha come ascissa la parte reale e come ordinata il coefficiente reale dell’unità immaginaria. 11

COORDINATE POLARI E NUMERI COMPLESSI • Usando il legame tra coordinate cartesiane e polari si ha: 12

RICORDI DI TRIGONOMETRIA • Formule di somma e sottrazione:

COORDINATE POLARI E NUMERI COMPLESSI • Dato il numero complesso z: e il numero complesso v : Il prodotto tra z e v è: 14

COORDINATE POLARI E NUMERI COMPLESSI • In particolare se z=v si ottiene: e in generale: Sono utili le Formule di De Moivre: 15

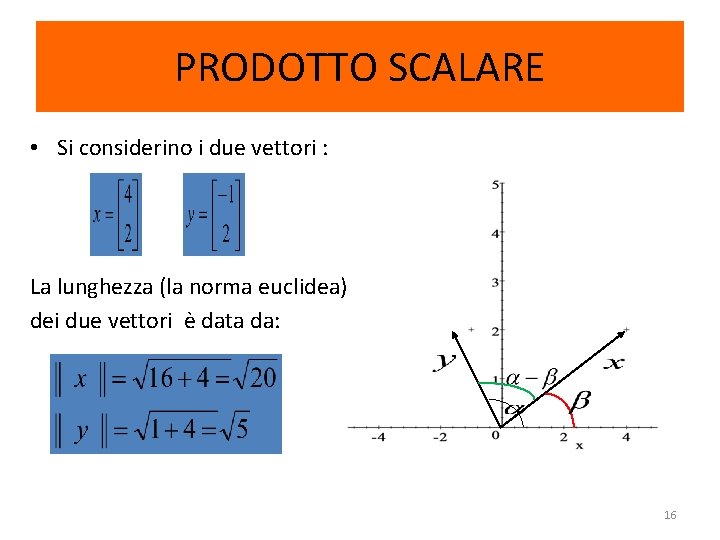
PRODOTTO SCALARE • Si considerino i due vettori : La lunghezza (la norma euclidea) dei due vettori è data da: 16

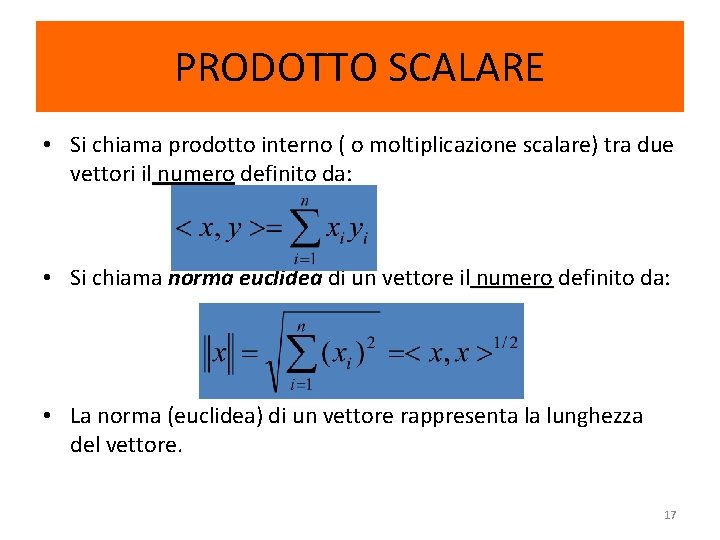
PRODOTTO SCALARE • Si chiama prodotto interno ( o moltiplicazione scalare) scalare tra due vettori il numero definito da: • Si chiama norma euclidea di un vettore ili numero definito da: • La norma (euclidea) di un vettore rappresenta la lunghezza del vettore. 17

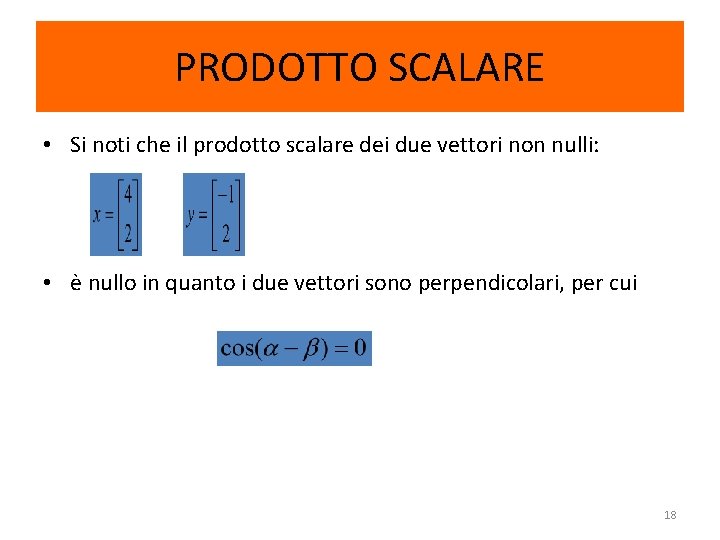
PRODOTTO SCALARE • Si noti che il prodotto scalare dei due vettori non nulli: • è nullo in quanto i due vettori sono perpendicolari, per cui 18

NORMA • Possono essere definite altri tipi di norma. • La norma di un vettore è una funzione che soddisfa: 1. 2. 3. 19

VETTORI ORTONORMALI • Dato un qualunque vettore di norma si può introdurre il vettore normalizzato espresso da: • Due vettori e si dicono ortonormali se sono ortogonali e ciascuno ha norma unitaria. • Se le colonne (o le righe) di una matrice sono a 2 ortonormali la matrice è ortogonale. 20

ESEMPIO: IL COEFFICIENTE DI CORRELAZIONE LINEARE • Esempio Si considerino i due vettori e costituiti dai prezzi di chiusura settimanale di 2 titoli nelle ultime settimane. Il coefficiente di correlazione lineare tra le due serie di prezzi può essere espresso da: dove rappresenta la media aritmetica dei prezzi di chiusura del titolo i-esimo. 21

ESEMPIO: IL COEFFICIENTE DI CORRELAZIONE LINEARE • Siano dati 2 titoli i cui prezzi di chiusura nelle ultime 4 settimane sono stati: • Il prezzo medio nelle ultime 4 settimane per ciascun titolo è dato dalla rispettiva media aritmetica 22

ESEMPIO: IL COEFFICIENTE DI CORRELAZIONE LINEARE • Per calcolare il coefficiente di correlazione lineare tra i 2 titoli è utile costruire i 2 vettori: • Per cui si ha: 23

SPAZI VETTORIALI Definizione ed esempi Si considerino 2 insiemi V e K. Si introducano 2 operazioni: • “composizione interna” tra elementi di V; • “composizione esterna” tra elementi di V ed elementi di K. Esempio 1. Composizione interna = somma tra matrici quadrate; Composizione esterna = prodotto di una matrice per uno scalare. 24

SPAZI VETTORIALI Definizione ed esempi Esempio 2 Sia V l’insieme dei polinomi algebrici di grado al massimo n. Composizione interna = somma tra polinomi; Composizione esterna = prodotto di un polinomio per uno scalare. N. B. Controllare cosa succede se V è l’insieme dei polinomi algebrici di grado n. 25

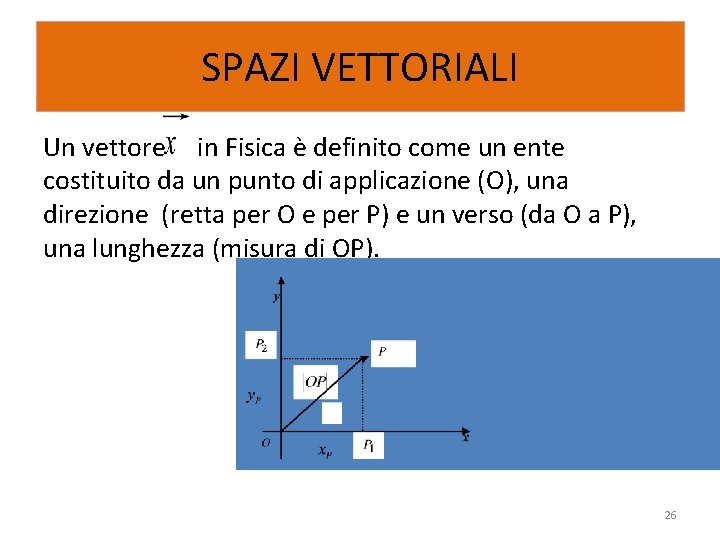
SPAZI VETTORIALI Un vettore in Fisica è definito come un ente costituito da un punto di applicazione (O), una direzione (retta per O e per P) e un verso (da O a P), una lunghezza (misura di OP). 26

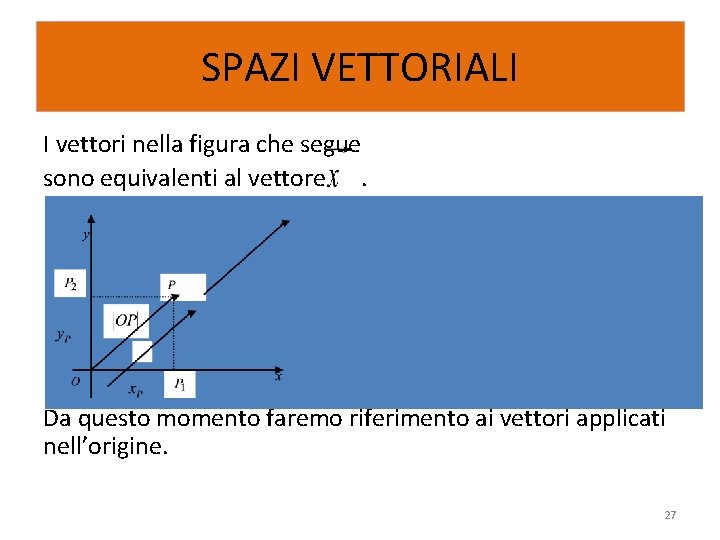
SPAZI VETTORIALI I vettori nella figura che segue sono equivalenti al vettore. Da questo momento faremo riferimento ai vettori applicati nell’origine. 27

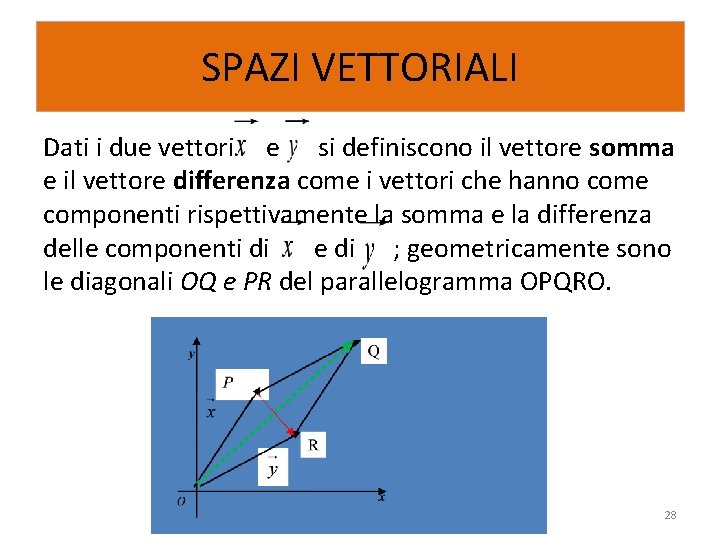
SPAZI VETTORIALI Dati i due vettori e si definiscono il vettore somma e il vettore differenza come i vettori che hanno come componenti rispettivamente la somma e la differenza delle componenti di e di ; geometricamente sono le diagonali OQ e PR del parallelogramma OPQRO. 28

COMBINAZIONE LINEARE Sia V uno spazio vettoriale rispetto al campo degli scalari K. Se W è sottoinsieme di V e W è a sua volta uno spazio vettoriale rispetto al campo degli scalari K, allora si dice che W è sottospazio vettoriale di V. Dati n elementi (vettori) di uno spazio vettoriale V ed n scalari si definisce combinazione lineare il vettore di V espresso da : 29

LINEARE INDIPENDENZA Gli n vettori dello spazio vettoriale V si dicono linearmente indipendenti se risulta se e solo se gli n scalari sono tutti contemporaneamente nulli. Se il vettore nullo si ottiene combinazione lineare di n vettori con coefficienti non tutti nulli allora i vettori si dicono linearmente dipendenti. 30

LINEARE DIPENDENZA Gli n vettori dello spazio vettoriale V sono linearmente dipendenti, e supponiamo che allora , dividendo per ovvero , si ottiene: è combinazione lineare degli altri vettori. 31

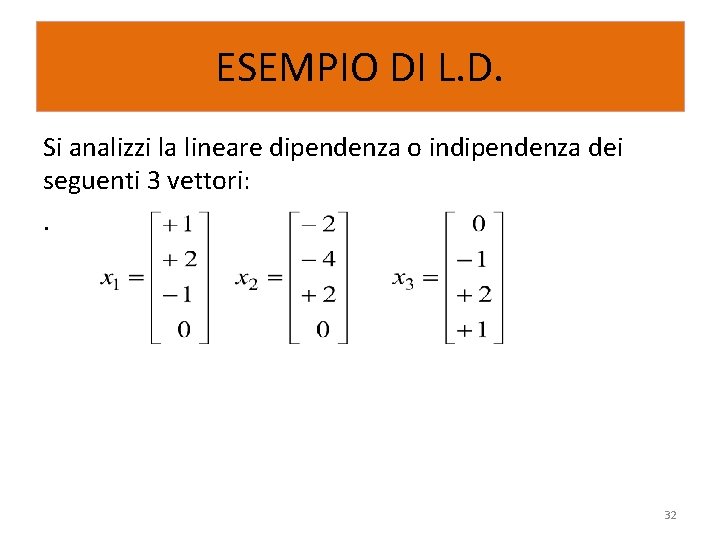
ESEMPIO DI L. D. Si analizzi la lineare dipendenza o indipendenza dei seguenti 3 vettori: . 32

SOLUZIONE DELL’ESEMPIO DI L. D. Per stabilire la dipendenza o indipendenza lineare dei 3 vettori, occorre determinare le soluzioni del sistema: 33

SOLUZIONE DELL’ESEMPIO DI L. D. La matrice dei coefficienti: ha rango 2, quindi il sistema ammette soluzioni : e risulta: 34

ESEMPIO 2 DI L. D. Si vuole esprimere il polinomio come combinazione lineare dei seguenti polinomi: 35

GENERATORI E BASI Dati gli n vettori dello spazio vettoriale V Sia l’insieme delle combinazioni lineari è un sottospazio vettoriale di e i vettori sono chiamati generatori di. Se h vettori tra gli n generatori sono linearmente indipendenti lo spazio vettoriale da essi generato coincide con. I vettori costituiscono una base di 36

GENERATORI E BASI I vettori costituiscono una base di. Il numero h dei vettori della base viene chiamato dimensione di. Dato un qualunque vettore esso può essere scritto come e i coefficienti della combinazione lineare vengono denominati coordinate (sono uniche!) del vettore rispetto alla base. Dato lo spazio vettoriale di dimensione h, esistono più basi. 37

GENERATORI E BASI Si considerino 2 basi di Un vettore può essere espresso nelle 2 basi da Ovvero come: Dove : 38

GENERATORI E BASI Uguagliando si ha da cui : ovvero La matrice cambiamento di base. è denominata matrice di 39

ESEMPIO DI GENERATORI E BASI Si consideri lo spazio vettoriale V dei polinomi algebrici di grado minore o uguale a 3: Si considerino i vettori di V : Essi sono generatori di V. Non sono linearmente indipendenti. I vettori sono linearmente indipendenti. 40

BASE CANONICA Si consideri lo spazio vettoriale V delle matrici quadrate di ordine 2. Una base è costituita da Si considerino i vettori di V : Sono una base per V, detta canonica. 41

ESEMPIO DI CAMBIAMENTO DI BASE Si considerino i 2 vettori dello spazio vettoriale delle matrici 2 x 1: Si determini la matrice di cambiamento di base rispetto alla base canonica. 42

TRASFORMAZIONI LINEARI Dati due spazi vettoriali W e si definisce trasformazione lineare di W in ogni funzione tale che: • • Nucleo di T, ker(T), è l’insieme dei vettori di W che hanno come immagine il vettore nullo di. Immagine di T, Im(T), è l’insieme di vettori di che provengono da vettori di W. 43

ESEMPIO DI T. L. Dati i due spazi vettoriali e si consideri la trasformazione lineare di in : • L’immagine della t. l. è l’insieme. Il nucleo di T, ker(T), è l’insieme dei vettori di che hanno come immagine il vettore nullo di , ovvero Da cui si ricava: Quindi 44

ESEMPIO DI T. L. Dati i due spazi vettoriali e si dimostri che la legge seguente è una trasformazione lineare : • dove Analogamente si dimostra che la trasformazione che associa al vettore la media aritmetica delle componenti è una trasformazione lineare: 45

ESEMPIO DI T. L. Si determini la trasformazione lineare tra e che fa corrispondere ad ogni vettore il vettore degli scarti dalla media aritmetica. • 46

TEOREMA DI RAPPRESENTAZIONE Si consideri la trasformazione lineare tra i due spazi vettoriali e , si può dimostrare il seguente teorema di rappresentazione: Se La trasformazione lineare viene denominata isomorfismo. 47

EQUAZIONE CARATTERISTICA Data una matrice quadrata A e un vettore x , il prodotto Ax definisce una trasformazione lineare Il vettore y è parallelo ad x se Da cui Il sistema lineare è soddisfatto da vettori non nulli solo se 48

EQUAZIONE CARATTERISTICA Data una matrice quadrata A, si definisce equazione caratteristica: ovvero: Le soluzioni vengono denominate autovalori. Le soluzioni del sistema: vengono denominate autovettori corrispondenti all’autovalore. 49

EQUAZIONE CARATTERISTICA Per l’equazione caratteristica valgono i seguenti teoremi: 1. Il coefficiente della potenza può essere ottenuto dalla somma degli minori principali di ordine i della matrice A moltiplicata per. 2. Il coefficiente della potenza può essere ottenuto dalla somma degli prodotti degli autovalori presi i alla volta moltiplicata per. 50

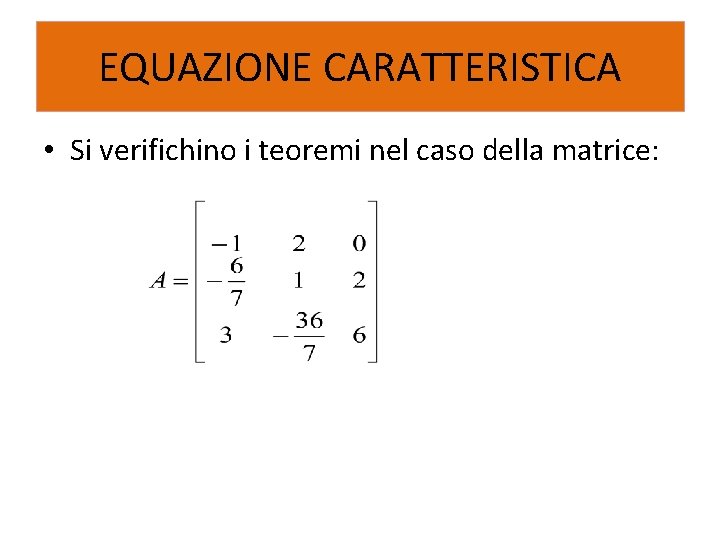
EQUAZIONE CARATTERISTICA • Si verifichino i teoremi nel caso della matrice:

EQUAZIONE CARATTERISTICA Teorema 3 “Una matrice quadrata ammette l’autovalore nullo se e solo il determinante è nullo”. Teorema 4 “Ogni matrice quadrata soddisfa la sua equazione caratteristica”.

EQUAZIONE CARATTERISTICA Teorema 5 “Se il rango di una matrice quadrata è r allora l’autovalore nullo ha molteplicità algebrica ”. Teorema 6 “Gli autovalori di una matrice triangolare coincidono con gli elementi della diagonale principale”.

MOLTEPLICITA’ Teorema 7 “Ad autovalori diversi corrispondono autovettori linearmente indipendenti”. Molteplicità algebrica Molteplicità geometrica Teorema 8 “La molteplicità algebrica dell’autovalore è maggiore o uguale alla molteplicità geometrica ”.

MATRICE MODALE Si definisce matrice modale della matrice A la matrice le cui colonne sono costituite dagli autovettori della matrice A” Teorema 9 “Gli autovalori di una matrice simmetrica sono reali” Teorema 10 “La matrice modale di una matrice simmetrica è ortogonale. ”

SISTEMI DI EQUAZIONI DIFFERENZIALI Un sistema di equazioni differenziali lineari è:

SISTEMI DI EQUAZIONI DIFFERENZIALI Un sistema di equazioni differenziali lineari omogeneo è:

SISTEMI DI EQUAZIONI DIFFERENZIALI Esempio 2.

SISTEMI DI EQUAZIONI DIFFERENZIALI Esempio 3.

SISTEMI DI EQUAZIONI DIFFERENZIALI Esempio 4.

EQUAZIONI DIFFERENZIALI Ø Funzioni che mettono in relazione una variabile indipendente ( es. x), una sua funzione ( es. y = f(x) ) e la derivata di quest’ultima ( es. y’ = f’ (x) ). ESEMPIO ØOrdine: massimo grado di derivazione che compare nell’equazione differenziale.

SOLUZIONI v. Generale ogni equazione differenziale ha infatti infinite soluzioni che differiscono per una costante. v. Particolare Si ottiene applicando la condizione iniziale alla soluzione generale trovata

APPLICAZIONI ECONOMICHE n Considereremo sistemi DINAMICI in cui avremo: Ø t : var. indipendente ( tempo ) Ø x( t ): var. dipendente (var. economica che si evolve nel tempo) Variabile di stato § Useremo questa notazione:

I SISTEMI DI EQUAZIONI DIFFERENZIALI NELLE APPLICAZIONI ECONOMICHE Saggio di variazione della variabile x al variare del tempo • Se “ cause del variare di x ” TERMINE DI CONTROLLO • sistema NON OMOGENEO • soluzioni diverse da quella banale • si può “guidare” la variabile x con opportuni interventi • Altrimenti • sistema OMOGENEO • ammette almeno la soluzione banale • la variabile x è incontrollabile

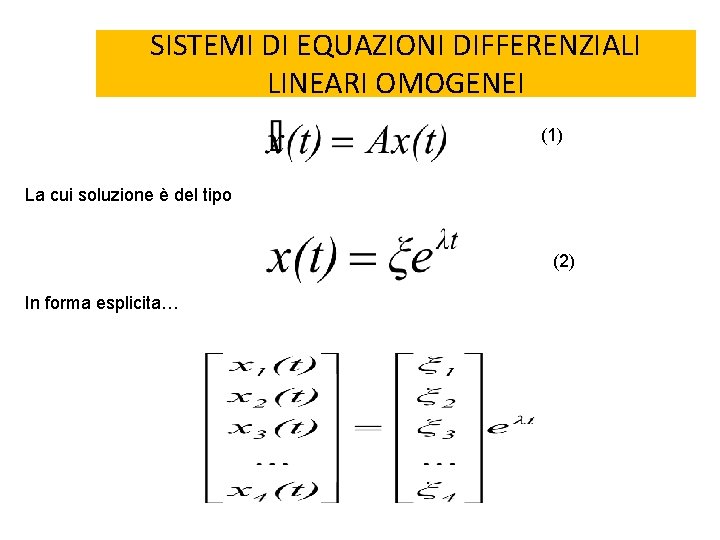
SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI OMOGENEI (1) La cui soluzione è del tipo (2) In forma esplicita…

SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI OMOGENEI Se la (2) è soluzione del sistema Il sistema omogeneo avrà soluzioni diverse da quella banale se: infinite soluzioni diverse da quella banale EQUAZIONE CARATTERISTICA DELLA MATRICE Cercare le soluzioni non nulle del sistema equivale a cercare gli autovalori di A e gli autovettori corrispondenti

SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI OMOGENEI Quindi le soluzioni del sistema saranno dove 1, 2, 3, …, n sono gli autovalori e sono gli autovettori corispondenti. (1), (2), (3)… (n)

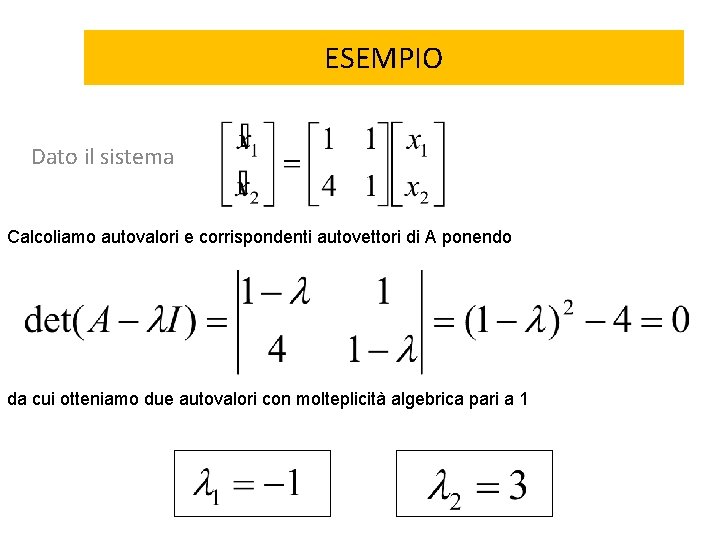
ESEMPIO Dato il sistema Calcoliamo autovalori e corrispondenti autovettori di A ponendo da cui otteniamo due autovalori con molteplicità algebrica pari a 1

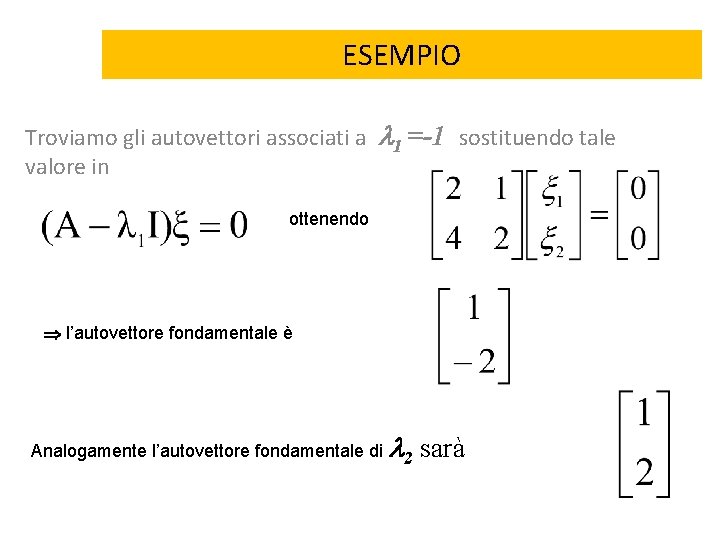
ESEMPIO Troviamo gli autovettori associati a valore in 1 =-1 sostituendo tale ottenendo l’autovettore fondamentale è Analogamente l’autovettore fondamentale di 2 sarà

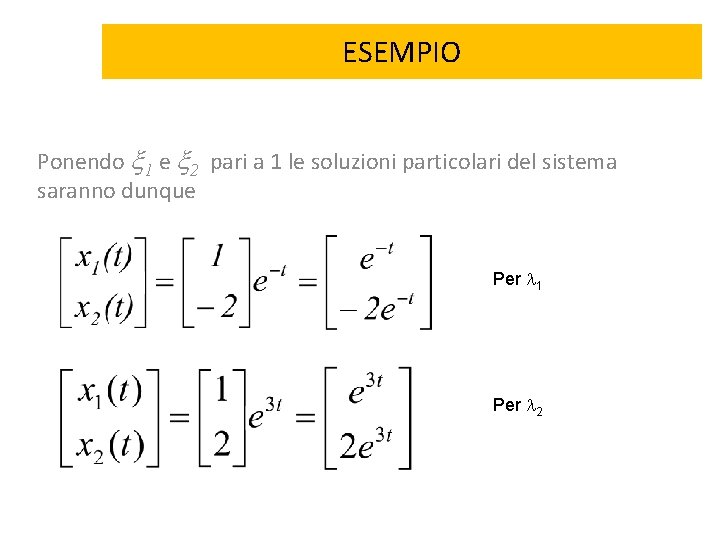
ESEMPIO Ponendo 1 e 2 pari a 1 le soluzioni particolari del sistema saranno dunque Per 1 Per 2

SOLUZIONI n. Se un sistema di equazioni differenziali omogeneo ammette soluzioni non nulle infinite soluzioni perché trovatane una se ne possono ricavare infinite attribuendo a valori arbitrari. n. Se due o più soluzioni linearmente indipendenti una qualunque loro combinazione lineare è a sua volta soluzione del sistema. n. Se è data una condizione iniziale la soluzione è unica

CONDIZIONI INIZIALI Se una condizione iniziale x(t 0) = x 0 Ø la soluzione del sistema ed è unica Ø Ø Si possono determinare c 1 e c 2 Graficamente si identifica una sola tra il fascio di possibili curve identificate dall’integrale generale. x(t) x 0 t

ESEMPIO L’integrale generale nell’esempio precedente era Se la condizione iniziale in t 0=o Applicando tale condizione all’integrale generale Da cui

ESEMPIO Sostituendo i valori trovati nell’integrale generale troviamo la soluzione particolare soluzione che: • È unica • Muta se cambia la condizione iniziale.

MATRICE FONDAMENTALE DELLE SOLUZIONI v Si ottiene affiancando i vettori delle soluzioni particolari in un sistema con due sole equazioni differenziali sarà: vÈ quadrata perché il numero delle soluzioni è sempre uguale al numero delle equazioni del sistema.

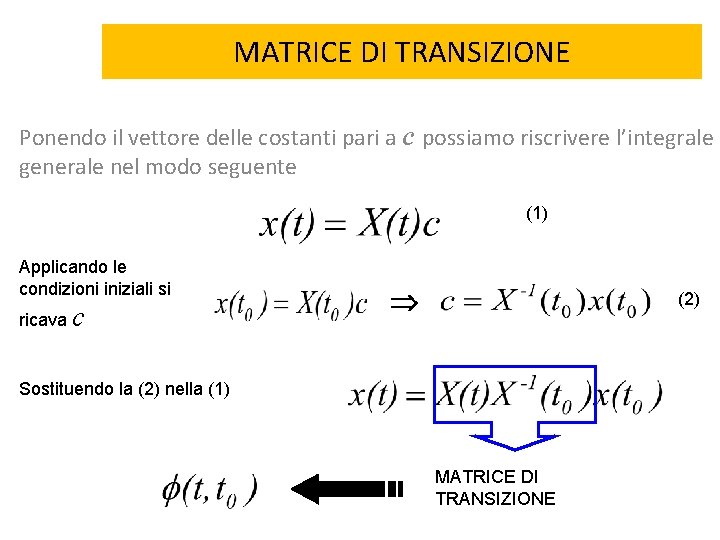
MATRICE DI TRANSIZIONE Ponendo il vettore delle costanti pari a c possiamo riscrivere l’integrale generale nel modo seguente (1) Applicando le condizioni iniziali si ricava c (2) Sostituendo la (2) nella (1) MATRICE DI TRANSIZIONE

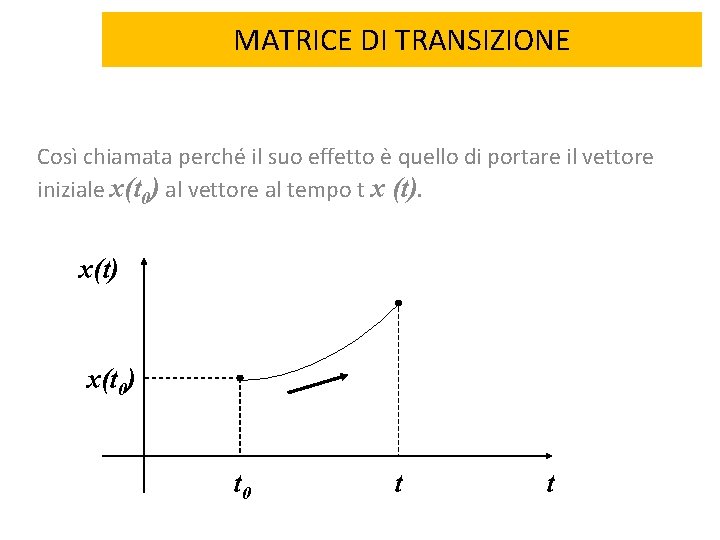
MATRICE DI TRANSIZIONE Così chiamata perché il suo effetto è quello di portare il vettore iniziale x(t 0) al vettore al tempo t x (t). x(t) x(t 0) t 0 t t

ESEMPIO La matrice fondamentale delle soluzioni è Data la condizione iniziale La matrice di transizione allora sarà

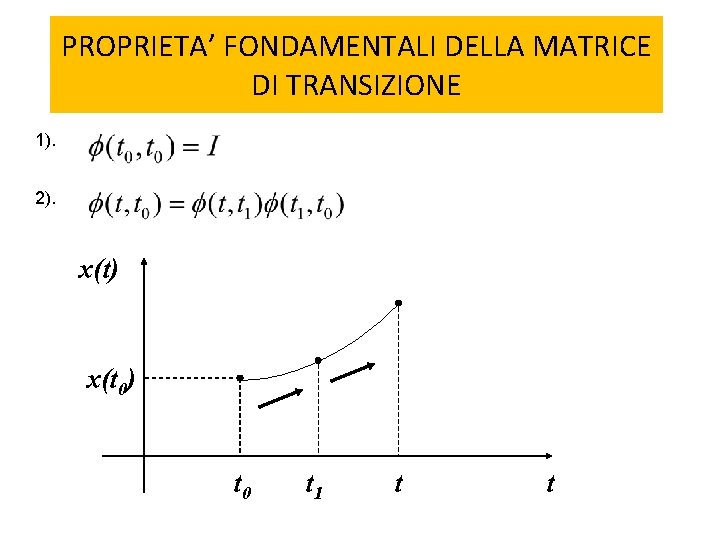
PROPRIETA’ FONDAMENTALI DELLA MATRICE DI TRANSIZIONE 1). 2). x(t) x(t 0) t 0 t 1 t t

PROPRIETA’ FONDAMENTALI DELLA MATRICE DI TRANSIZIONE 3). x(t) x(t 0) t 0 t t 4). Anche la matrice di transizione è una soluzione del sistema

ESEMPIO 2 Dato il sistema con calcoliamo gli autovalori imponendo L’equazione caratteristica diventa Le cui soluzioni sono (autovalori di A) m. a. = 2 m. a. = 1

ESEMPIO 2 Cerchiamo gli autovettori per 1 = 2= -1 risolvendo il sistema In forma matriciale n-r = 2 soluzioni, dove Da cui vn ordine di (A- I) vr rango di (A- I)

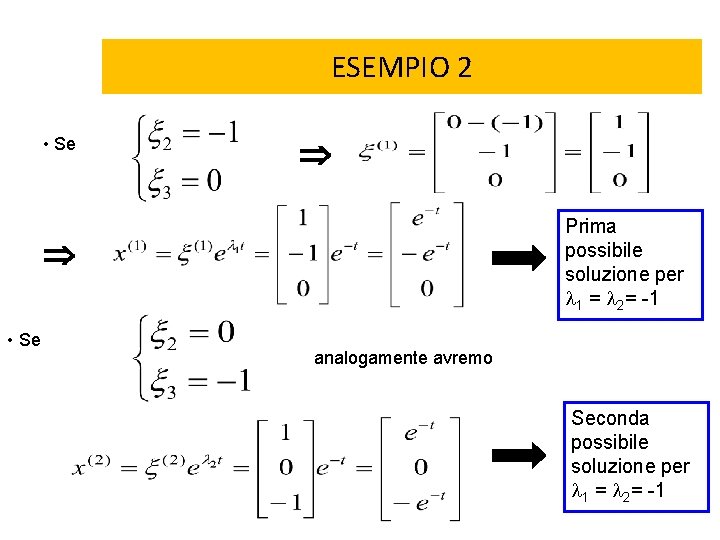
ESEMPIO 2 • Se Prima possibile soluzione per 1 = 2= -1 • Se analogamente avremo Seconda possibile soluzione per 1 = 2= -1

ESEMPIO 2 Cerchiamo ora gli autovettori per 3= 2 risolvendo il sistema ossia Da cui quindi, se 3 =1 possibile soluzione per 3= 2

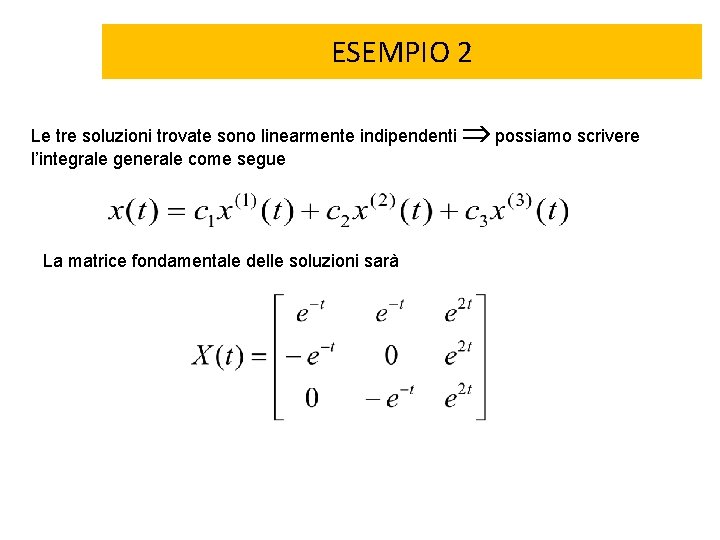
ESEMPIO 2 Le tre soluzioni trovate sono linearmente indipendenti possiamo scrivere l’integrale generale come segue La matrice fondamentale delle soluzioni sarà

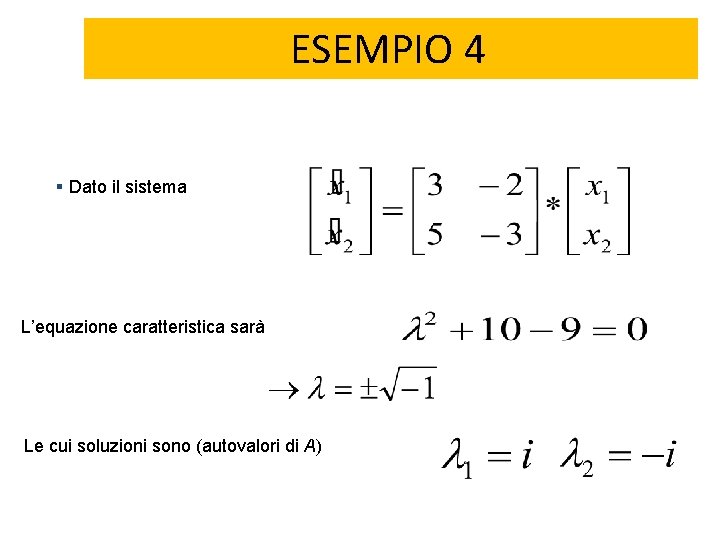
ESEMPIO 4 § Dato il sistema L’equazione caratteristica sarà Le cui soluzioni sono (autovalori di A)

ESEMPIO 4 Come si può notare sono numeri complessi e coniugati. Cerchiamo gli autovettori per 1 = i risolvendo il sistema

ESEMPIO 4 Si noti che per costruzione il rango di (A- I)=0 è quindi minore di 2 perciò questo sistema ha: • = soluzioni • Inoltre, il rango è maggiore di 0 perché non è una matrice nulla. Si evince perciò che la soluzione del sistema equivale a quella di una delle sue equazioni.

ESEMPIO 4 • Scegliamo la seconda: Perciò un autovettore associato a sarà:

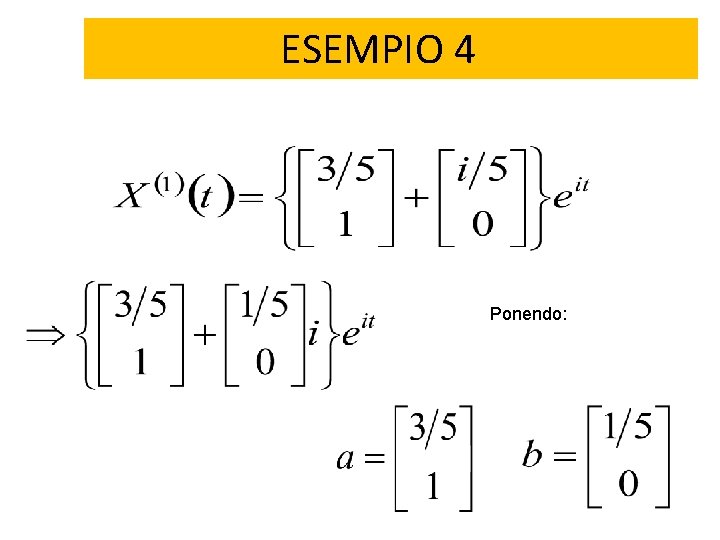
ESEMPIO 4 Ponendo ad esempio si ottiene una delle possibili soluzioni del sistema dato: Qualsiasi valore assuma nel campo dei numeri reali, l’autovettore relativo a sarà sempre di tipo complesso e potrà essere scritto nella forma che separa la parte reale da quella immaginaria.

ESEMPIO 4 Ponendo:

ESEMPIO 4 Si ha: Ora possiamo calcolare l’ autovettore corrispondente a e si ottiene: e perciò l’autovettore corrispondente analogamente a quanto fatto per l’altro valore sarà:

ESEMPIO 4 Questi due autovettori non sono reali, né linearmente indipendenti, caratteristiche essenziali per poter costruire l’integrale generale del sistema di equazioni dato. E’ necessario introdurre un metodo che permetta di passare da una espressione non reale ad una reale.

ESEMPIO 4 • Supponiamo di aver trovato due autovalori della matrice A del tipo: In corrispondenza dei due autovalori si trovano gli autovettori Con a e b vettori reali

ESEMPIO 4 • Posto poi , le corrispondenti soluzioni del sistema di equazioni differenziali saranno:

ESEMPIO 4 • Consideriamo per ora solo la prima delle due espressioni, la si può scrivere: Ricordando la formula di De Moivre

ESEMPIO 4 • Possiamo scrivere: In questo modo si è ottenuta l’espressione di x(t) in una forma in cui il primo termine è reale ed il secondo è formato da un coefficiente reale per un numero immaginario.

ESEMPIO 4 • Se poniamo: Si può dimostrare che y(1) ed y(2) sono soluzioni reali e linearmente indipendenti del sistema

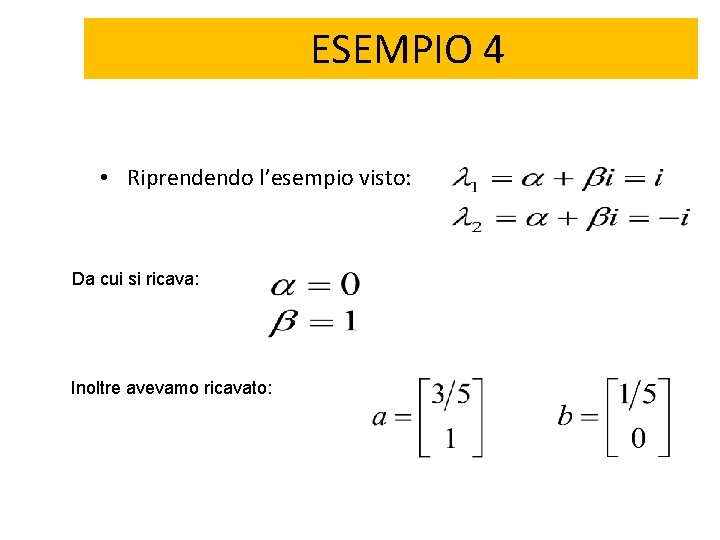
ESEMPIO 4 • Riprendendo l’esempio visto: Da cui si ricava: Inoltre avevamo ricavato:

ESEMPIO 4 • Possiamo scrivere subito le due soluzioni reali e linearmente indipendenti

ESEMPIO 4

ESEMPIO 4 • Adesso posso calcolare l’integrale generale, posta la condizione iniziale: t=0 Si può calcolare l’integrale generale combinazione lineare delle due soluzioni particolari :

ESEMPIO 4 • Per trovare il valore di c si risolve il sistema:

ESEMPIO 4