Matematica e statistica Versione didascalica parte 2 Sito

Matematica e statistica Versione didascalica: parte 2 • • • Sito web del corso http: //www. labmat. it/didattica Docente: Prof. Sergio Invernizzi, Università di Trieste e-mail: inverniz@units. it

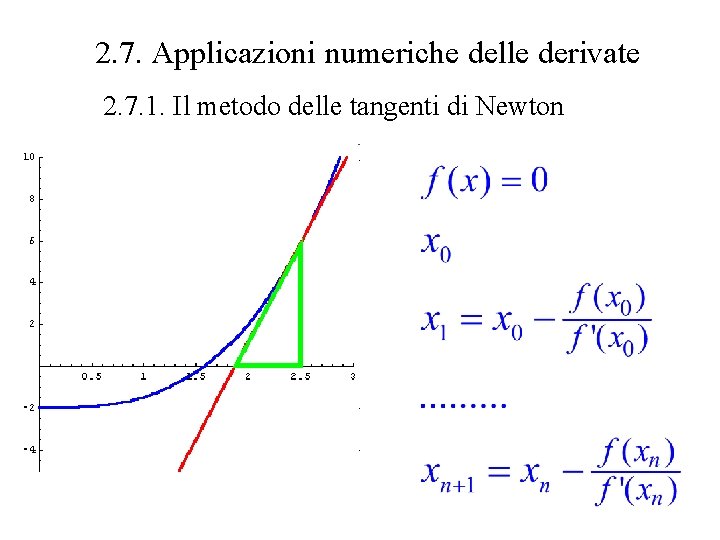
2. 7. Applicazioni numeriche delle derivate 2. 7. 1. Il metodo delle tangenti di Newton

2. 7. 1. Il metodo delle tangenti di Newton > y 1 <- function(x) exp(x)-2. > y 2 <- function(x) exp(x) > y 3 <- function(x) x - y 1(x)/y 2(x) > y 3(2) [1] 1. 270671 > newton <- function(x) y 3(y 3(y 3(x))))) > newton(2) [1] 0. 6931472 > log(2) [1] 0. 6931472 > y 1 <- function(x) x^2 -2 > y 2 <- function(x) 2*x > newton(2) [1] 1. 414214 > sqrt(2) [1] 1. 414214

> y 1 <- function(x) sin(x)-x^2 > y 2 <- function(x) cos(x)-2*x > 1 -> a > y 3(a) -> a; a [1] 0. 891396 > y 3(a) -> a; a [1] 0. 8769848 > y 3(a) -> a; a [1] 0. 8767263 > y 3(a) -> a; a [1] 0. 8767262 > y 1(a) [1] 0

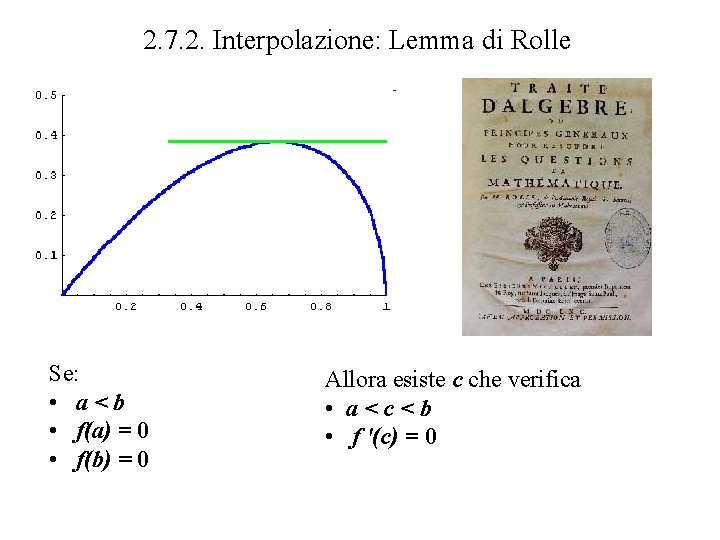
2. 7. 2. Interpolazione: Lemma di Rolle Se: • a<b • f(a) = 0 • f(b) = 0 Allora esiste c che verifica • a<c<b • f '(c) = 0

2. 7. 2. a. Interpolazione costante (di Lagrange) valore vero = valore approssimato + errore

2. 7. 2. a. Interpolazione costante (di Lagrange)

2. 7. 2. b. Interpolazione lineare (di Lagrange) valore vero = valore approssimato + errore

2. 7. 2. b. Interpolazione lineare (di Lagrange)

2. 7. 3. Funzioni crescenti e decrescenti • f (x) è crescente in un intervallo I se comunque presi due valori u < v nell’intervallo si ha f (u) f (v). • f (x) è decrescente in un intervallo I se comunque presi due valori u < v nell’intervallo si ha f (u) f (v). • f (x) è costante in un intervallo I se comunque presi due valori u < v nell’intervallo si ha f (u) = f (v).

Applicazione dell’interpolazione costante una quantità positiva • f '(x) 0 in ogni x di un intervallo I f (x) è crescente nell’intervallo I • f '(x) 0 in ogni x di un intervallo I f (x) è decrescente nell’intervallo I • f '(x) = 0 in ogni x di un intervallo I f (x) è costante nell’intervallo I

2. 7. 4. Funzioni convesse e concave • f (x) è convessa in un intervallo I se comunque presi due valori u < v nell’intervallo I si ha f (x) r (x) per tutti gli x del sottointervallo [u, v] • f (x) è concava in un intervallo I se comunque presi due valori u < v nell’intervallo I si ha f (x) r (x) per tutti gli x del sottointervallo [u, v] • f (x) è lineare in un intervallo I se comunque presi due valori u < v nell’intervallo I si ha f (x) = r (x) per tutti gli x del sottointervallo [u, v] Qui la r(x) è la retta che passa per (u, f(u)) e (v, f(v)), cioè la funzione lineare che in x = u ed x = v assume gli stessi valori di f.

Applicazione dell’interpolazione lineare una quantità negativa • f "(x) 0 in ogni x di un intervallo I f (x) è convessa nell’intervallo I • f "(x) 0 in ogni x di un intervallo I f (x) è concava nell’intervallo I • f "(x) = 0 in ogni x di un intervallo I f (x) è lineare nell’intervallo I

Mnemotecnica

Dinamica di popolazioni, I • X = X(t) popolazione al tempo t, ovviamente X(t) > 0 • Tasso di crescita costante: X '/ X = a, ossia X ' = a. X • a > 0 popolazione crescente, < 0 decrescente, = 0 costante • X " = a. X ' = a a. X = a²X > 0 X = X(t) convessa (sia che cresca, sia che decresca) • Si ottengono informazioni su X(t) senza risolvere la equazione (senza conoscere la formula per X(t) =. . . ) • Si parla di analisi qualitativa del problema. • Si dimostra che X(t) = X(0) exp(a t)

Dinamica di popolazioni, II • X = X(t) popolazione al tempo t, ovviamente X(t) > 0 • Tasso di crescita decrescente linearmente: X '/ X = a – b. X, ossia X ' = a. X – b. X 2 = X (a – b. X) • Negli intervalli di tempo in cui X < a/b la popolazione è crescente • Negli intervalli di tempo in cui X > a/b la popolazione è decrescente • X " = a. X ' – 2 b. XX ' = X '(a – 2 b. X) • Negli intervalli di tempo in cui X < (a/b)/2 la popolazione è crescente, e la crescita è convessa. • Negli intervalli di tempo in cui (a/b)/2 < X < a/b la popolazione cresce ma la crescita è concava. • Negli intervalli di tempo in cui X > a/b la popolazione decresce, in modo convesso. - fare il grafico! -

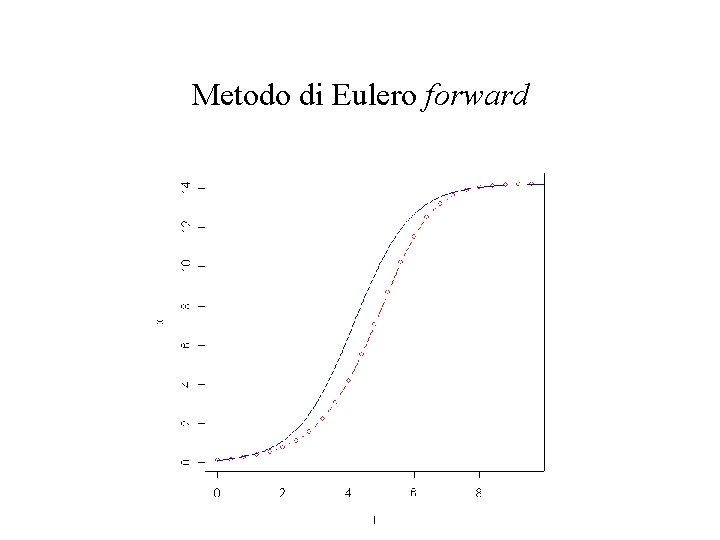
• Metodo di Eulero in avanti, o forward (standard) (derivata = quoziente di Newton destro): per il futuro essendo (valore iniziale assegnato) • Variante: Metodo di Eulero indietro, o backward (derivata = quoziente di Newton sinistro): per il passato

Metodo di Eulero forward > > > > a <- 1. 14 b <- 0. 08 f <- function(x) a*x-b*x^2 u <- function(x) (20. 0550*exp(1. 14*x))/(161. 642+1. 40737*exp(1. 14*x)) h <- 0. 4 t 0 <- 0. x 0 <- 0. 123 t <- c(1: 25)*NA x <- c(1: 25)*NA t[1] <- t 0 x[1] <- x 0 for (n in c(2: 25)) { t[n] <- t[n-1]+h; x[n] <- x[n-1]+ h*f(x[n-1]) } plot(t, x, type="b", col="red") plot(u, 0, 10, add=TRUE, col="blue")

Metodo di Eulero forward

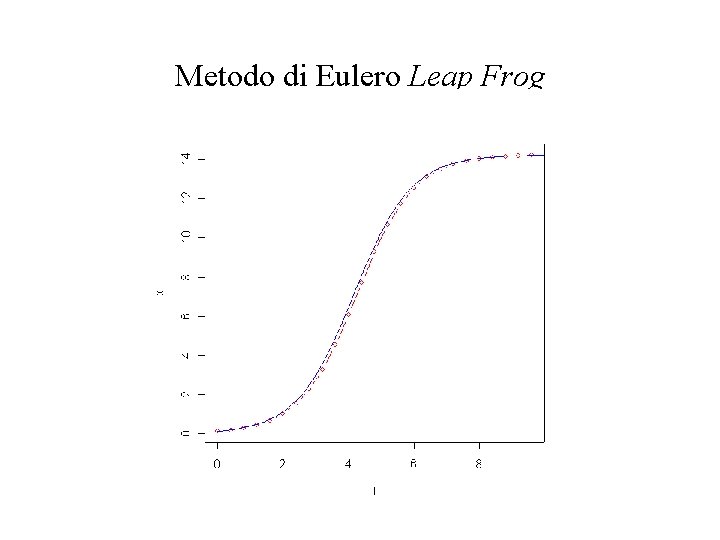
• Metodo Leap Frog, o della cavallina (derivata = differenza centrale) essendo e dove (valore iniziale assegnato) (secondo valore calcolato con il metodo di Eulero forward)

Metodo di Eulero Leap Frog > > > x[1] <- x 0 x[2] <- x[1] + h*f(x[1]) for (n in c(3: 25)) { x[n] <- x[n-2]+ 2*h*f(x[n-1]) } plot(t, x, col="red", type="b") plot(u, 0, 10, add=TRUE, col="blue")

Metodo di Eulero Leap Frog

Attenzione! • Per questi tipi di modelli (equazioni differenziali) devono sempre essere usati integratori professionali! • No fai-da-te! • Problemi di “stabilità”