Matemaatiline statistika Matemaatiliseks statistikaks nimetatakse matemaatika haru mis

Matemaatiline statistika Matemaatiliseks statistikaks nimetatakse matemaatika haru, mis tõenäosusteooriale tuginedes uurib statistiliste andmete põhjal järelduste tegemise meetodeid.

Mark Twain: on kolme sorti valesid: – lihtne vale (hädavale) – häbematu vale – statistika

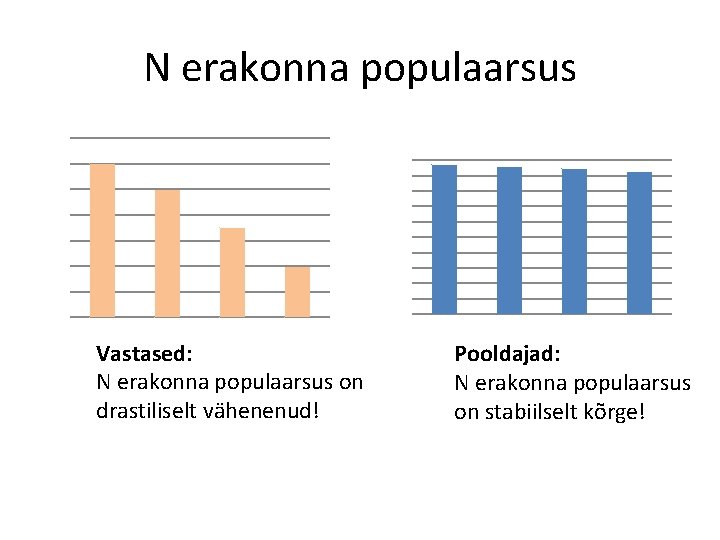
N erakonna populaarsus Vastased: N erakonna populaarsus on drastiliselt vähenenud! Pooldajad: N erakonna populaarsus on stabiilselt kõrge!

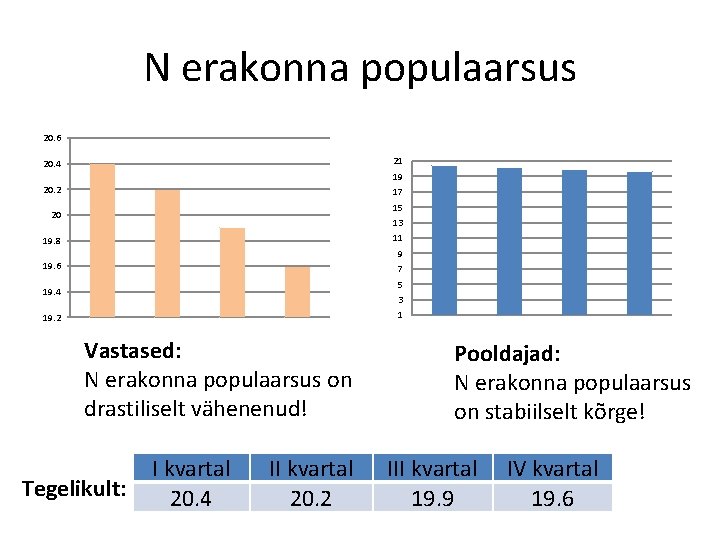
N erakonna populaarsus 20. 6 21 20. 4 19 20. 2 17 15 20 13 11 19. 8 9 19. 6 7 5 19. 4 3 1 19. 2 Vastased: N erakonna populaarsus on drastiliselt vähenenud! Tegelikult: I kvartal 20. 4 II kvartal 20. 2 Pooldajad: N erakonna populaarsus on stabiilselt kõrge! III kvartal 19. 9 IV kvartal 19. 6

Põhimõisted, seosed • Üldkogum - kõikide antud liiki objektide hulk, mille kohta järeldusi soovitakse teha • Valim – uurimiseks võetud üldkogumi osa • Nõuded valimile – võrdne võimalus valimisse sattuda – proportsionaalsus – küllalt arvukas valim peab olema esindav ehk representatiivne

• Tunnus – objekti iseloomustav näitaja • Tunnuste liigitamine – arvulised (kvantitatiivsed tunnused) • pidevad (pikkus, kaal, temperatuur jne) • diskreetsed (lehekülgede arv, õpilaste arv jne) – mittearvulised (kvalitatiivsed tunnused) • järjestatud tunnus (väga hea, rahuldav) – binaarne tunnus (on/ei ole; +/-) • nominaalne tunnus (silmade värv, rahvus) • Ettevaatlik tuleb olla “arvutamisel” mittearvuliste tunnustega.

Näited 1. Kui mingi objekti kaal on 4 kg ja teise objekti kaal on 2 kg, siis üks on teisest kaks korda raskem. Aga: Kas hinne „ 4“ on kaks korda parem kui hinne „ 2“? /Kuulutus: vahetan kaks „kahte“ ühe „nelja“ vastu. /

• Milline peaks olema koondhinne? 445555 5 4 444455 • Avalikustame nende hinnete punktid: 75 75 90 90 keskm. 85 /hinne “ 4”/ 85 85 100 keskm. 90 /hinne “ 5”/

2. Olgu rühmas 10 inimest, tunnusena sugu on märgitud M– 3 N– 7 Mõttetu on arvutada nö keskmist (keskmine sugu).

• Statistiline rida – tunnuse väärtused andmete hankimise järjekorras – Näit. üliõpilane uuris teatud taimeliikide õite omadusi, ühe tunnusena sai ta andmed õie kaalu kohta: 13, 11, 10, 12, 13, 15, 11, 14, 12, 12, 14 • Statistilise rea maht – tunnuse väärtuste arv – õie kaalu korral maht N = 13 • Variatsioonrida – tunnuse väärtused kasvavas või kahanevas järjekorras – Õie kaalude variatsioonrida on 10, 11, 12, 12, 13, 14, 14, 15

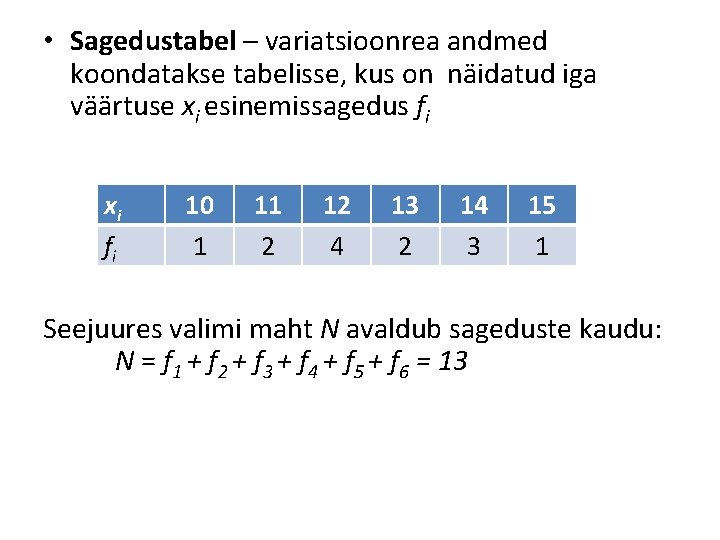
• Sagedustabel – variatsioonrea andmed koondatakse tabelisse, kus on näidatud iga väärtuse xi esinemissagedus fi xi fi 10 1 11 2 12 4 13 2 14 3 15 1 Seejuures valimi maht N avaldub sageduste kaudu: N = f 1 + f 2 + f 3 + f 4 + f 5 + f 6 = 13

• Jaotustabel – iga väärtuse xi kohta näidatakse tema esinemise suhtelist sagedust Suhtelist sagedust võib lugeda võrdseks antud väärtuse tõenäosusega. xi 10 11 12 13 pi Seejuures suhteliste sageduste summa: p 1 + p 2 + p 3 + p 4 + p 5 + p 6 = 1 14 15

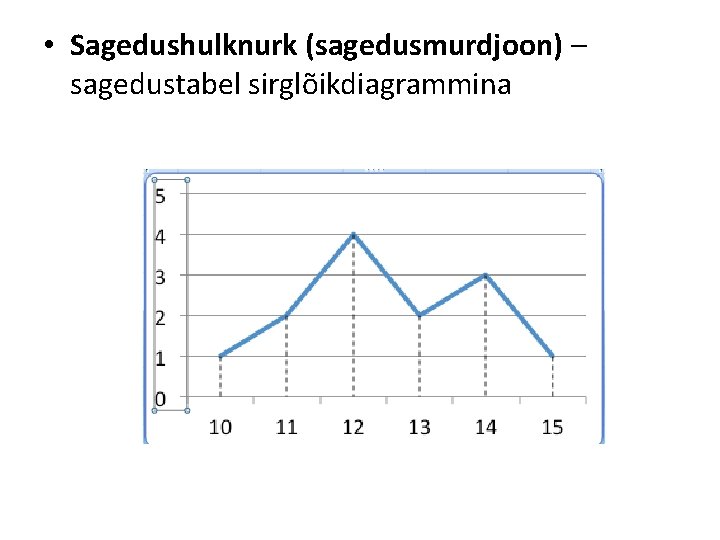
• Sagedushulknurk (sagedusmurdjoon) – sagedustabel sirglõikdiagrammina

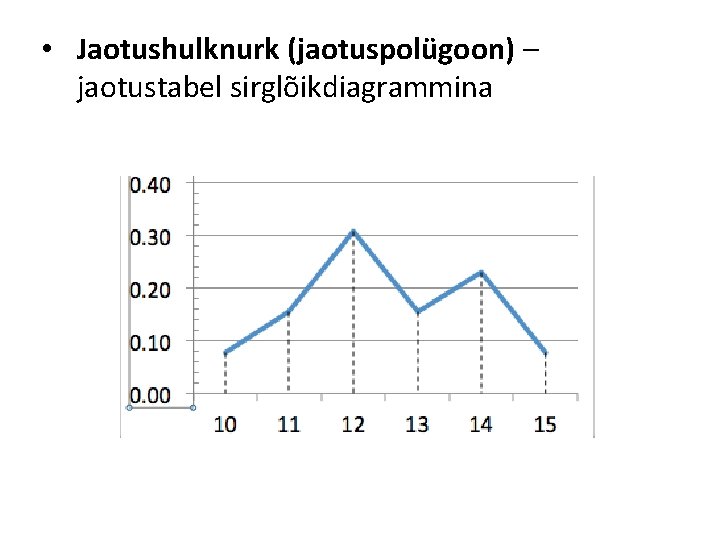
• Jaotushulknurk (jaotuspolügoon) – jaotustabel sirglõikdiagrammina

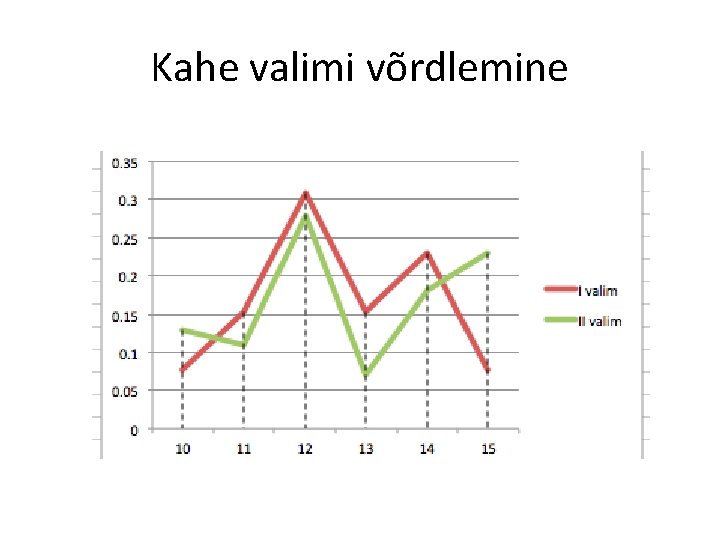
Kahe valimi võrdlemine

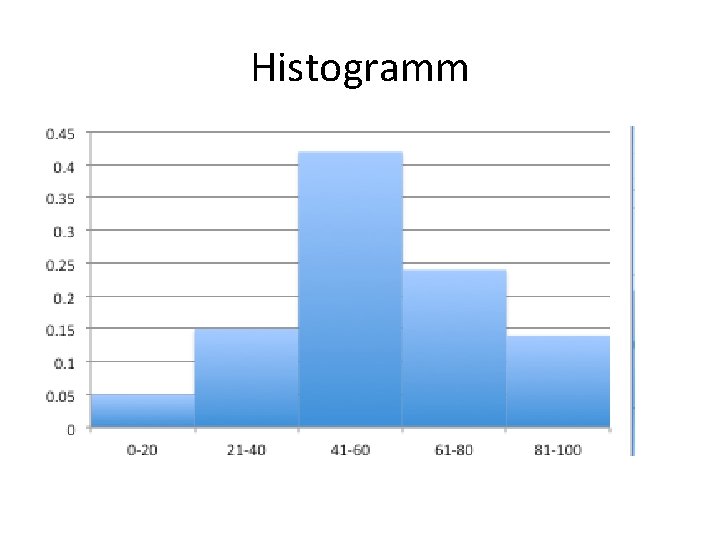
Sagedus-, jaotustabel vahemikena 0 -20 0, 05 21 -40 0, 15 41 -60 0, 42 61 -80 0, 24 88 -100 0, 14

Histogramm

Ülesanded • Ül 149 • Ül 150

Nr 149 Milline järgmistest tunnustest on arvuline, mittearvuline, pidev, diskreetne: nimi sugu sünniaasta haridus kasv vanus kinganumber töötasu töökoht

Nr 150 • Meeste kingakaupluses müüdi ühe tunni jooksul 20 paari kingi numbritega 39, 41, 40, 41, 44, 40, 42, 43, 39, 42, 41, 42, 38, 42, 41, 43, 41, 39, 40. Mis tüüpi on vaadeldava kogumi tunnus? Koostada sagedustabel. Milliseid kingi müüdi kõike enam, milliseid kõige vähem?

Andmeanalüüs Arvkarakteristikud: • asendi karakteristikud – aritm. keskmine e keskväärtus – mediaan – mood • hajuvuse karakteristikud – variatsioonrea ulatus – dispersioon, standardhälve – variatsioonikordaja

Keskväärtus • Tunnuse keskväärtuseks on tunnuse väärtuste aritmeetiline keskmine. • Tšebõševi (Chebychev) suurte arvude seadus – katseliselt määratava suuruse tõelise väärtuse parimaks lähendiks on katsetulemuste aritmeetiline keskmine, mis on seda usaldusväärsem, mida pikema katseseeria põhjal see on leitud.

Keskväärtuse variatsioonrea korral Variatsioonrea (õite kaalud) 10, 11, 12, 12, 13, 14, 14, 15 korral:

Keskväärtus sagedustabeli korral (kaalutud aritmeetiline keskmine) seejuures Õite kaalude korral xi fi 10 1 11 2 12 4 13 2 14 3 15 1

Keskväärtus jaotustabeli korral kusjuures Õite kaalu jaotustabeli korral xi pi 10 11 12 13 14 15

Keskväärtus vahemikega antud tabeli korral Lisatakse rida vahemiku “esindajaga” (otspunktide aritmeetiline keskmine) xi pi 0 -20 0, 05 21 -40 0, 15 41 -60 0, 42 61 -80 81 -100 0, 24 0, 14

Keskväärtus vahemikega antud tabeli korral Lisatakse rida vahemiku “esindajaga” (otspunktide aritmeetiline keskmine) xi pi 10 0 -20 0, 05 30, 5 21 -40 0, 15 50, 5 41 -60 0, 42 70, 5 90, 5 61 -80 81 -100 0, 24 0, 14 Keskväärtus leitakse “esindajate” kaudu

Ülesanded keskväärtuse leidmisele • Nr 158 • Nr 159 (vt lk 43)

Nr 158 • Algaja laskuri tulemused on esitatud tabelina. Leida keskmine silmade arv ühe lasuga. xi fi 1 1 2 1 3 0 4 2 5 5 6 9 7 7 8 9 9 8 10 8

Nr 159 • Leida kummagi klassi kontrolltöö keskmine hinne. A xi pi 2 11% 3 25% 4 36% 5 28% xi pi 2 0, 09 3 0, 23 4 0, 41 5 0, 27 B

Mediaan • Mediaaniks nimetatakse tunnuse väärtust, millest suuremaid (või võrdseid) ja väiksemaid (või võrdseid) liikmeid on variatsioonreas ühepalju. • Tähistus: Me

Mediaani leidmine • Olgu antud variatsioonrida 10, 12, 14, 16, 18 • Kui variatsioonreas on paarisarv liikmeid, siis tuleb leida keskmiste aritmeetiline keskmine: 10, 12, 14, 16, 18, 20

Mediaani leidmine • Olgu antud variatsioonrida 10, 12, 14, 16, 18 Me = 14 (3. liige) • Kui variatsioonreas on paarisarv liikmeid, siis tuleb leida keskmiste aritmeetiline keskmine: 10, 12, 14, 16, 18, 20 Me = (14 + 16): 2 = 15 /3. ja 4. liikme aritm. keskmine/

Mediaani leidmine üldkujul • Kui liikmeid on paaritu arv, siis • Kui liikmeid on paarisarv, siis

Mediaani leidmine sagedustabeli korral Kuna maht on paaritu arv, siis mediaaniks peab olema 7. liige; alustame liikmete lugemist vasakult poolt ning leiame sageduste reast, et 1 + 2 + 4 = 7, seega mediaan on 12: Me = 12

Mediaani leidmine jaotustabeli korral xi pi 10 0, 1 20 0, 25 30 0, 25 Leiame nn 50% piiri. Kuna 0, 1 + 0, 25 = 0, 35 < 0, 50 ja 0, 1 + 0, 25 = 0, 6 > 0, 50 siis 50% piir vastab x-i väärtusele 30. Seega Me = 30 40 0, 3 50 0, 1

Mediaani leidmine vahemikega tabeli korral xi pi 0 -20 0, 05 21 -40 0, 15 41 -60 0, 42 61 -80 0, 24 81 -100 0, 14 Leiame nn mediaanvahemiku: 0, 05 + 0, 15 = 0, 20 < 0, 50 0, 05 + 0, 15 + 0, 42 = 0, 62 > 0, 50 Mediaanvahemikuks on 41 -60. Mediaaniks võime võtta selle vahemiku esindaja: Me = 50, 5

Mood • Moodiks nimetatakse tunnuse kõige sagedamini esinevat väärtust. • Kui kõikide väärtuste esinemine on samasuguse sagedusega, siis mood puudub. • Kui on kaks erinevat sama sagedusega väärtust, siis on tunnus bimodaalne.

Näited moodi leidmise kohta Mo = 12 xi pi 10 0, 1 20 0, 35 30 0, 35 40 0, 1 Mo 1 = 20 xi fi 10 2 20 2 30 2 40 2 50 0, 1 Mo 2 = 30 50 2 Mood puudub.

Ülesanded • Nr 167 • Nr 166 • Leida õpperühma pikkuste mediaan • Nr 173

Nr 167 • Algaja laskuri tulemused on esitatud tabelina. Leida keskmine silmade arv ühe lasuga. xi fi 1 1 2 1 3 0 4 2 5 5 6 9 7 7 8 9 9 8 10 8

Nr 166 • Teha vajalikud küsitlused ning teatada vastus! Aega on 2 minutit.

Ülesanne • Leida õpperühma õpilaste pikkuste mediaan; aega on 2 minutit! Eeldame, et igaüks teab oma pikkust! Võib liikuda ringi!

Nr 173 • VALE: • ÕIGE: I klassi hinnete summa: II klassi hinnete summa: Keskmine:

Hajuvusmõõdud • Kohale võistkonnas konkureerib kaks laskurit. Nad teevad 10 proovilasku. Kumba laskurit eelistada? 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. A 5 8 6 9 10 8 10 6 8 9 B 8 8 7 5 8 8 10 9

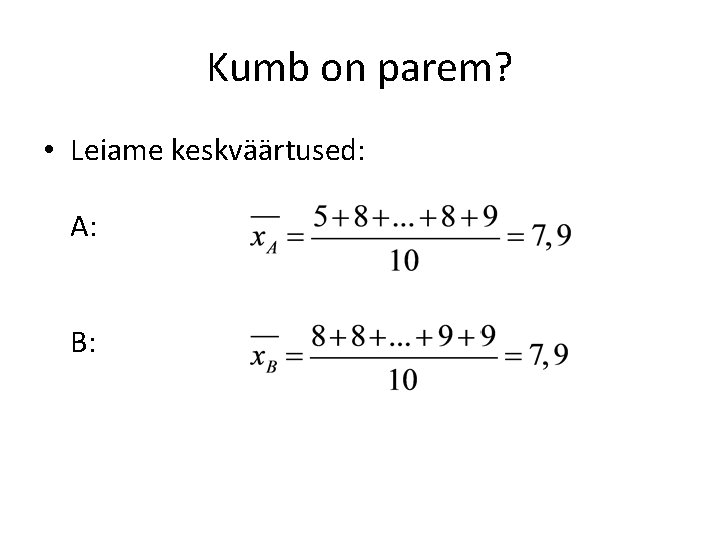
Kumb on parem? • Leiame keskväärtused: A: B:

Mille poolest laskurite seeriad erinevad? • Kuidas hinnata hajuvust? • Tuleks kasutusele võtta mingi arvnäitaja, mis iseloomustaks hajuvust keskmise ümber.

Hajuvusmõõdud • variatsioonrea ulatus: /mõlemal laskuril sama/ • erinevus keskväärtusest ehk hälve:

• Hälve iseloomustab iga üksiku väärtuse xi erinevust keskväärtusest. • Et iseloomustada andmestiku kui terviku hajuvust, on vaja üldisemat näitajat. • Ei sobi nn keskmine hälve, sest hälvete keskmine on alati null.

• Et vältida hälvete vastastikust koondumist, kasutatakse hajuvuse iseloomustajana hälvete ruutude aritmeetilist keskmist e dispersiooni.

Dispersioon ja standardhälve • Mida suurem on dispersioon, seda suurem on tunnuse hajuvus. • Dispersiooni ühikuks on tunnuse ruutühik. Puudub võimalus võrdluseks näiteks keskväärtusega. • Standardhälve – ruutjuur dispersioonist:

Standardhälve fi - sagedused N - objektide koguarv - hälvete ruudud

Sagedustabel võistleja A jaoks xi 5 6 7 8 9 10 fi 1 2 0 3 2 2

Sagedustabel võistleja A jaoks xi 5 6 7 8 9 10 fi 1 2 0 3 2 2

Sagedustabel võistleja A jaoks xi 5 6 7 8 9 10 fi 1 2 0 3 2 2

Sagedustabel võistleja A jaoks xi 5 6 7 8 9 10 fi 1 2 0 3 2 2 -2, 9 -1, 9 -0, 9 0, 1 1, 1 2, 1

Sagedustabel võistleja A jaoks xi 5 6 7 8 9 10 fi 1 2 0 3 2 2 -2, 9 -1, 9 -0, 9 0, 1 1, 1 2, 1 8, 41 3, 61 0, 81 0, 01 1, 21 4, 41

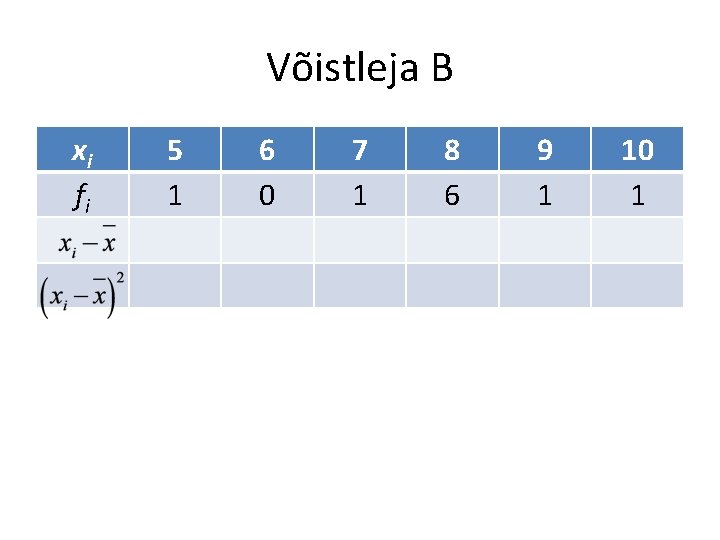
Võistleja B xi fi 5 1 6 0 7 1 8 6 9 1 10 1

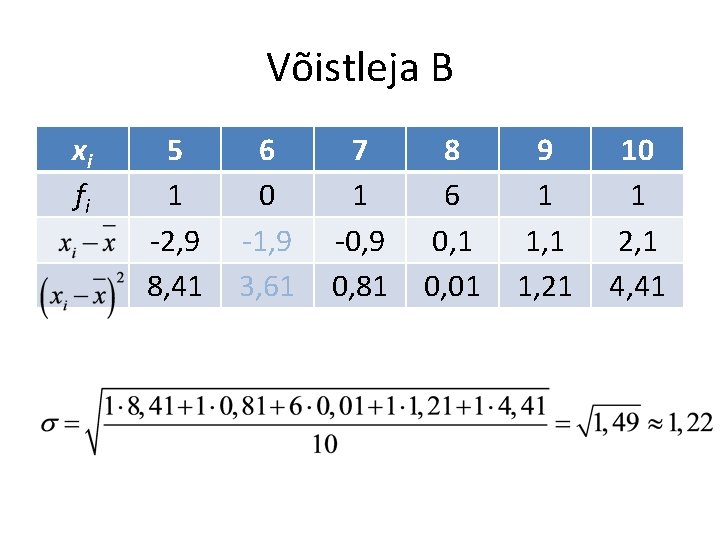
Võistleja B xi fi 5 1 -2, 9 8, 41 6 0 -1, 9 3, 61 7 1 -0, 9 0, 81 8 6 0, 1 0, 01 9 1 1, 21 10 1 2, 1 4, 41

Kokkuvõte • Võistleja A näitajad: • Võistleja B tulemused on stabiilsemad, sest hajuvus on väiksem.

Variatsioonikordaja • Hajuvusmõõt, mida kasutatakse erinevate valimite võrdlemisel, kui keskväärtused on erinevad (või tunnuste väärtused on erinevates ühikutes). • Variatsioonikordaja:

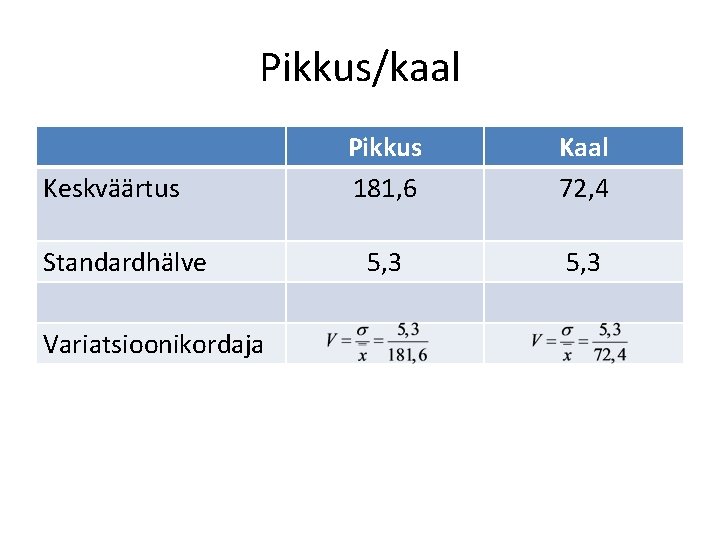
Variatsioonikordaja rakendamine Noormeeste andmed on variatsioonreana. Kumb tunnus hajub rohkem, kas kaal või pikkus? pikkus 175 178 kaal 64 70 180 73 185 75 190 80 Kummalegi tunnusele leiame keskväärtuse, standardhälbe ning variatsioonikordaja.

Pikkus/kaal Keskväärtus Standardhälve Variatsioonikordaja Pikkus 181, 6 Kaal 72, 4 5, 3

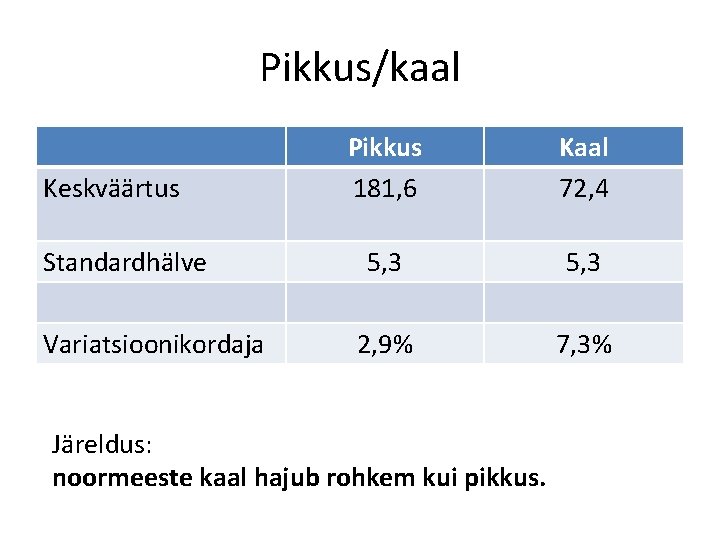
Pikkus/kaal Keskväärtus Standardhälve Variatsioonikordaja Pikkus 181, 6 Kaal 72, 4 5, 3 2, 9% 7, 3% Järeldus: noormeeste kaal hajub rohkem kui pikkus.

Ülesanne Kumb hajub rohkem, kas elevantide kaal või liblikate tiibade siruulatus? Leida sobivad karakteristikud. Elevantide mass (kg): 5300, 6240, 5910, 6010, 5070; liblikate tiibade siruulatus (mm): 45, 48, 50, 55, 60, 65, 70.

Lahendus • Elevantide kaal: • Liblikate tiivad: Tiibade siruulatus hajub rohkem.

Tund on lõppenud!