Matemaatika kasulikkus prof Andi Kivinukk Tallinna likooli matemaatika

Matemaatika kasulikkus ? prof Andi Kivinukk Tallinna Ülikooli matemaatika osakond TALLINNA SAKSA GÜMNAASIUM Matemaatikanädal 04. 02. 2013 - 08. 02. 2013

Teemad • • • Mis on matemaatika ? Matemaatika tänapäeva ühiskonnas Veidi modelleerimisest, eriti funktsioonide abil Kauba pakkumine (tootja) ja nõudlus (tarbija) Kauba hinna dünaamika ( diferentsvõrrand )

Mis on matemaatika ? • Algul (e. Kr. ) oli geomeetria (trigonomeetria) – navigeerimine tähistaeva järgi, niisutussüsteemid, ehitus (püramiidid) • Võrrandite (a x + b = 0) lahendamine • Tuletised/integraalid – suur revolutsioon (19. s. mehaanika matematiseerimine) • 20. s. hulgateooria ja moodne matemaatika (struktuurid, suur spetsialiseerumine)

Matemaatika olemus • Kui matem-a oleks ülesannete lahendamine, siis kõik muutuks aina keerulisemaks • Õnneks suure hulga faktide kogunemisel toimub struktuuride (mustrite) loomine (lahendati ruut-, kuupjne edasi võrrandeid, kuni leiti üldine teooria) • Modelleerimine (see juba kasulik) • Matemaatika terviklikkus (algebra, geomeetria, matemaatiline analüüs jne – kõik omavahel läbi põimunud) • Ilu printsiip (ilus säilib : a 2 + b 2 = c 2 ) • Konkreetne matemaatik ei mõtle kasutoomisele, kuid tervikuna on matemaatika suure kasuteguriga (vaja ainult pliiatsit/paberit)

Matemaatika ja ühiskond Matemaatika mõju ühiskonnale (ja vastupidi) toimub selle rakenduste kaudu, mis tänapäeval baseeruvad oluliselt arvutitel. Nobeli majanduspreemiat (rääkimata füüsikast/keemiast, ka meditsiinist) saab valdavalt ainult matemaatika rakendustega seotud tööde eest

CAD (Computer Aided Design) autotööstuses kirjeldab auto kuju ja see esitatakse kohe ka arvutiekraanil matemaatiliste funktsioonidega - need on ruut- ja kuuppolünoomide „kokkuliimitud sugulased”. Eeldab nn mitmeharuliste funktsioonidega (F(x) = f(x), kui a<x<b ja F(x) = g(x), kui b<x<c) tutvumist. Lihtsaim näide on murdjoon.

GPS (Global Positioning System), mis kasutab asjaolu, et kui meie kaugused kolme satelliidini on teada, siis saame üheselt määrata oma asukoha kolm koordinaati. Ka ilmaennustamine kuulub osaliselt siia (vt ETV-s ilmakaarti, kus pilved liiguvad) Tegelikult mittetriviaalne ülesanne, sest satelliidid liiguvad.

Arvutitomograafia (kui kehast lasta läbi röntgenikiir, siis olenevalt keha omadustest see neeldub, seda mõõdetakse ja tulemused liidetakse kuidagi kokku, mis viib teatud integraalideni; selle eest on saadud Nobeli meditsiinipreemia) NB! Integraali tutvustamine pindala ja summade abil on õpetlikum, kui formaalne definitsioon

MP 3 (ja uuemad versioonid) MP 3 -süsteemi matemaatiline väljatöötamine algas ca 25 aastat tagasi ja see baseerub täiesti uut tüüpi funktsioonidel, mis on siinuste-koosinuste „sugulased” ja mis võimaldavad hääle digitaalset teisendamist (audio coding) 12 -15 korda kiiremini võrreldes varasemate meetoditega

Digipildindus (kõik noored on kasutanud digikaameraid või saatnud JPG formaadis pilte): iga pilt koosneb kahe muutuja funktsiooni väärtustest, milledega tuleb teha „kavalaid” teisendusi, et need väärtused pakkida internetti ja siis meie kodus jälle pildiks lahti pakkida. NB! Maatriksarvutus on siin tähtis.

Pilt ca 83 tuh baiti (1 bait on digitaalse info ühik, nt (1, 0, 0, 1, 0, 1))

Pilt ca 1500 baiti

Teadete salastamine (krüptograafia) • Internetiajastul (al 1970) algas suuremahuline infovahetus, mida osaliselt (pangad, armeed, firmad) oli vaja salastada • Uus matemaatiline idee: avaliku võtmega kodeerimine (RSA – Rivest, Shamir, Adelman (MIT) ). Kodeerimine toimub suurte, juhuslikult genereeritud algarvude korrutamisel, p*q = N, kuid dekodeerimine N teguriteks lahutamisel

Modelleerimisest • Mudel on reaalsuse abstraktsioon, kuid peab kirjeldama reaalsuse olulisi külgi • Matemaatilised mudelid on funktsioonid, võrrandid (nende süsteemid) jne, mis sisaldavad parameetreid • Parameetrid teevad kirjelduse paindlikuks, nende muutmisega saab teha analüüsi • Reaalse elu (nt majanduslikud) süsteemid püüdlevad tasakaaluolekut (matemaatiliselt on max/min)

Lineaarse nõudlus- ja pakkumisfunktsiooniga turu mudel Turg = tarbijad (nõuavad kaupa) + tootjad (pakuvad kaupa) q – kauba kogus, p – kauba ühiku hind Tarbija nõudmine oleneb hinnast: q = D(p) – nõudlusf-n (Õpilased harjunud: y = D (x) ) (demand). D(p) on kahanev ! Tootja pakkumine oleneb hinnast: q = S(p) – pakkumisf-n (supply). S(p) on kasvav ! Lineaarsed mudelid lihtsamad: D(p) = a – b p; S(p) = c + d p (0 < a, b, c, d - parameetrid) N. D(p) = 5 – 2 p ; S(p) = 1 + 2 p (a=5, b=d=2, c=1)

Mudel D(p) = a – b p; S(p) = c + d p (a=5, b=d=2, c=1) Tasakaal, kui D(p) = S(p) = q ehk vaja lahendada süsteem q=a–bp q=c+dp Determinantidega saame: p* = (a - c) / (b + d), q* = (ad + bc) / (b + d) Nõue mudelile: a > c Analüüs: 1) kui a kasvab, siis p*, q* kasvavad 2) kui c kasvab, siis p* kahaneb ja q* kasvab

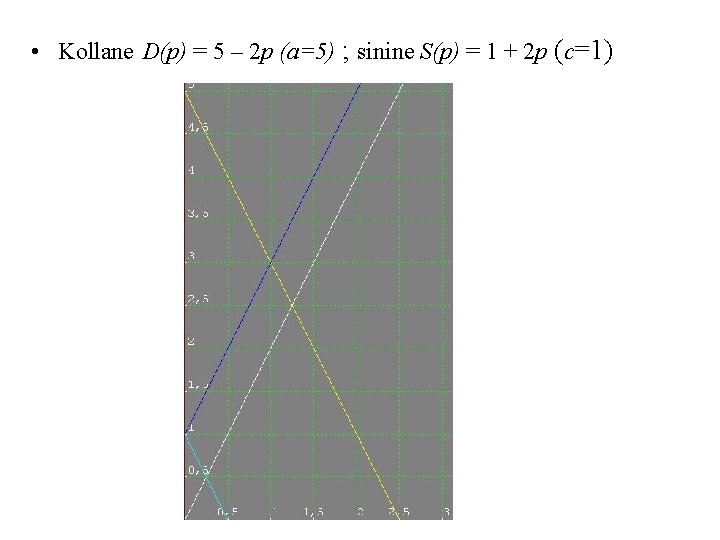
• Kollane D(p) = 5 – 2 p (a=5) ; sinine S(p) = 1 + 2 p (c=1)

Lineaarse nõudlus- ja pakkumisfunktsiooniga turu dünaamika Ajamomentidel n = 0, 1, 2, … olgu turul kauba hind vastavalt p n ja kaupa nõutakse kogus D n ning pakutakse S n + 1 (see tähendab, et pakkumine päeval n + 1 oleneb eelmise päeva hinnast p n ) Võrranditega: Dn = a - b pn ; Sn+1 = c + d pn Turu tasakaal tähendab: Saame: S n + 1 = D n+ 1 c + d p n = a - b p n +1 = A p n + B (*) (A = - d /b < 0, d – tootmise kiirus (intensiivsus), b – tarbimise kiirus; B = (a – c) /b > 0)

Näide 1. a=5, b=d=2, c=1, siis p n +1 = - p n + 2 Arvutame : olgu p 0 = 1. 5, siis p 1 = 0. 5, p 2 = 1. 5, p 3 = 0. 5, … Üldjuhul A = -1 korral p n +1 = - p n + B saame : olgu p 0 , siis p 1 = B - p 0, p 2 = - (B - p 0) + B= p 0 , … Hind kõigub kahe väärtusena : p 0 või B - p 0 !

Näide 2. p n +1 = - 0. 5 p n + 2 Arvutame: olgu p 0 = 1. 5, siis p 1 = 1. 25, p 2 = 1. 375, p 3 = 1. 3125, p 4 = 1. 34375, p 5 = 1. 328125, … Hind tundub stabiliseeruvat, aga milliseks väärtuseks ? Oletame, et piirväärtuseks on p* = ? Saame p*=-0. 5 p*+2 ehk p*=2/1. 5=1. 333. . .

Näide 3. p n +1 = - 1. 5 p n + 2 Arvutame: olgu p 0 = 1. 5, siis p 1 = - 0. 25, p 2 = 2. 375, p 3 = - 1. 5625, p 4 = 4. 34375, p 5 = - 4. 515625, … Midagi enneolematut ? Mõned hinnad negatiivsed ? ? ?

Lineaarne dünaamiline süsteem p n +1 = A p n + B (*) Saab tõestada, et (*) lahend on : p n = ( p 0 – B / (1 - A) ) A n + B / (1 - A) Edasi: a) kui - 1 < A (< 0 ), siis eksisteerib lim p n = B / (1 - A) ; b) kui - 1 = A , siis p 2 n = p 0 , p 2 n + 1 = B - p 0 ; c) kui A < - 1 , siis | lim p n | = lõpmatus.

Näide mittelineaarsest dünaamilisest süsteemist Nõudmine: D n = 3 - 2 p n ; Pakkumine: S n + 1 = p n 2 + 1 Turu tasakaal : S n + 1 = D n+ 1 ehk p n 2 + 1 = 3 - 2 p n+1 , millest p n +1 = 1 - p n 2 / 2 (**) Seda analüütiliselt lahendada ei saa, aga arvutada saab (4 kohta peale koma). Olgu p 0 = 1. 0, siis p 1 = 0. 5, p 2 = 0. 875, p 3 = 0. 6172, p 4 = 0. 8095, p 5 = 0. 6724, p 6 = 0. 7739, p 7 = 0. 7005, p 8 = 0. 7546, p 9 = 0. 7153… Vist stabiliseerub kuskile ? Geomeetriliselt “ämblikuvõrgu” meetod !

http: //en. wikipedia. org/wiki/Cobweb_plot Vaatame ! Seal võrrand p n +1 =3 ( p n - p n 2 ) ja p 0 = 0. 08, p 1 = 0. 22, p 2 = 0. 516 jne. Teisel joonisel on p n +1 =r ( p n - p n 2 ) , kus 1 ≤ r ≤ 4. Vt http: //www. tlu. ee/~andik opakademia_2011

Kokkuvõte • Matemaatika on kasulik • Matemaatika on huvitav • Matemaatika on tänapäeval paljude teaduste alus TULGE ÕPPIGE MATEMAATIKAT, VÄHEMALT NII PALJU, ET SUUDATE OMA ERIALAL TEHA KAASAEGSET TEADUST!