MatchingBased Algorithm for FPGA Channel Segmentation Design YaoWen

Matching-Based Algorithm for FPGA Channel Segmentation Design Yao-Wen Chang, Jai-Ming Lin, and M. D. F. Wong IEEE Transactions on Computer-Aidded Design of Integrated Circuits and Systems, June 2001 Speaker : 江振龍 Date : 10/17/2003

Outline Introduction ØRow-based FPGA architecture ØThe tradeoff between performance and routability Channel Segmentation Design ØProblem Formulation ØSegmentation Design Algorithm Experimental Results Conclusion

Introduction
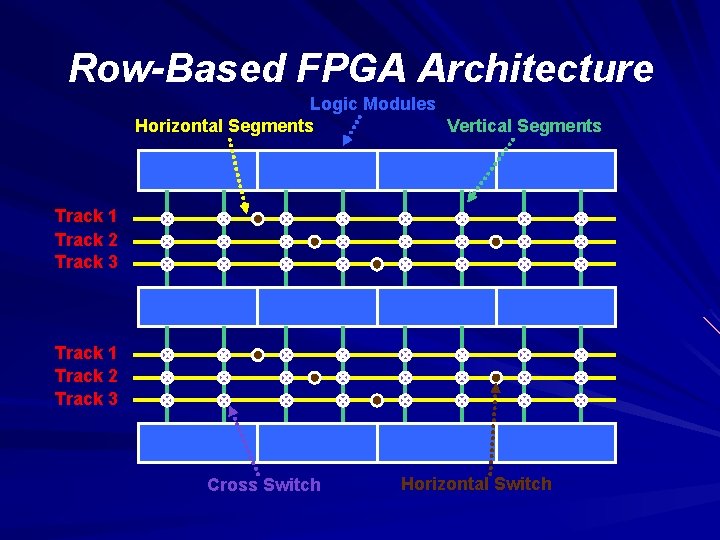
Row-Based FPGA Architecture Logic Modules Vertical Segments Horizontal Segments Track 1 Track 2 Track 3 Cross Switch Horizontal Switch
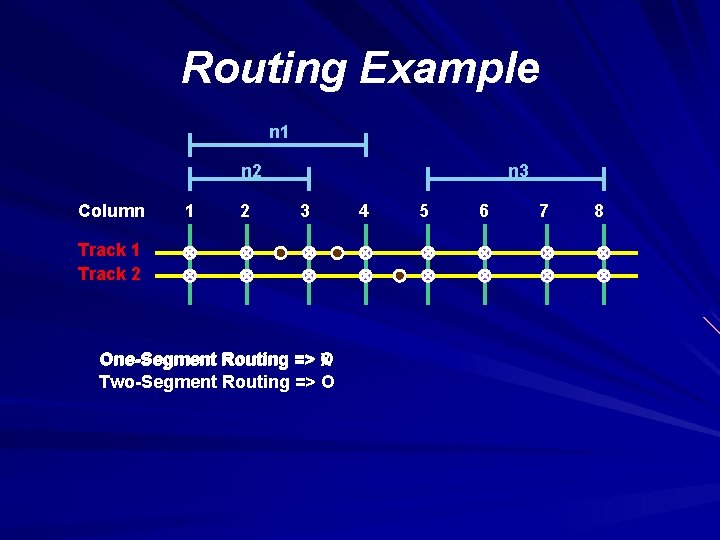
Routing Example n 1 n 2 Column 1 2 n 3 3 Track 1 Track 2 O One-Segment Routing => X Two-Segment Routing => O 4 5 6 7 8

The tradeoff between performance and routability Switch has high R and C => Delay Better Performance Ø Ø For each track - fewer horizontal switches and segments For each segment - longer length Reduce routability Waste more wire Routability Ø Ø For each track - more horizontal switches and segments For each segment - shorter length Nets can be routed with more flexibility Less waste of wire How to determine a segmentation distribution to maxmize the routability under performance constraints ?

Channel Segmentation Design

Problem Formulation Best Routability ØAccommodate as many routing instances as possible Problem Formulation ØGiven L , T , K , m , and n, design a channel segmentation to maxmize the success rate for K-segment routing
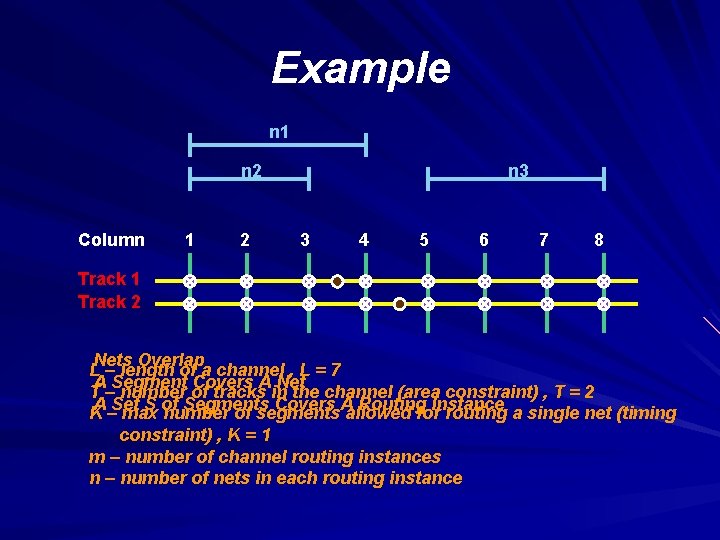
Example n 1 n 2 Column 1 2 n 3 3 4 5 6 7 8 Track 1 Track 2 Nets Overlap L – length of a channel , L = 7 A Segment Covers A Net T – number of tracks in the channel (area constraint) , T = 2 A Set S of Segments Covers A Routing Instance K – max number of segments allowed for routing a single net (timing constraint) , K = 1 m – number of channel routing instances n – number of nets in each routing instance

Segmentation Design Algorithm Flow – The matching-and-merging stage Net matching problem Tree-like bottom-up merging manner – The tuning stage Left-edge algorithm Track Constraint – The filling stage Determine the switch location on the tracks Fill the empty space between each pair of intervals in the T tracks to form a set of segments

Net Matching Problem Find a set of nets to cover each of two sets of nets with least length Given two finite sets I and J of nets , find a matching M such that Length(Union(I, J)) is minimized
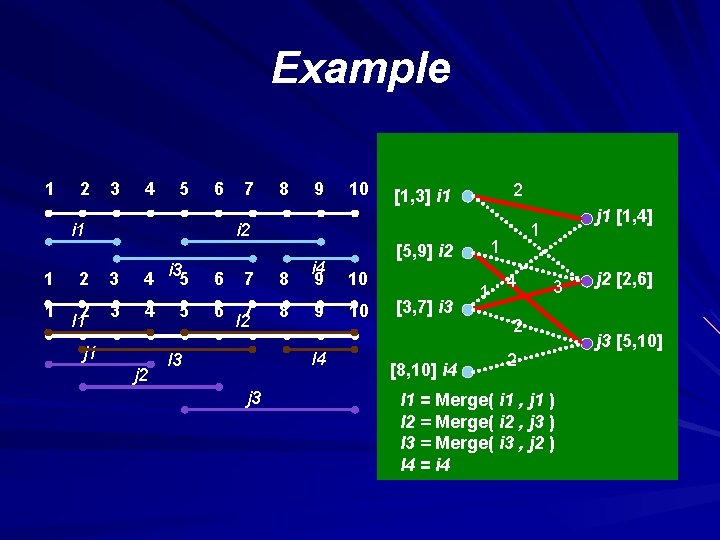
Example 1 2 3 4 5 6 i 1 7 8 9 10 2 [1, 3] i 1 i 2 1 2 3 4 i 3 5 6 7 8 i 4 9 10 1 2 I 1 3 4 5 6 7 I 2 8 9 10 j 1 j 2 I 4 I 3 j 3 1 [5, 9] i 2 [3, 7] i 3 [8, 10] i 4 1 j 1 [1, 4] 1 4 3 2 2 I 1 = Merge( i 1 , j 1 ) I 2 = Merge( i 2 , j 3 ) I 3 = Merge( i 3 , j 2 ) I 4 = i 4 j 2 [2, 6] j 3 [5, 10]
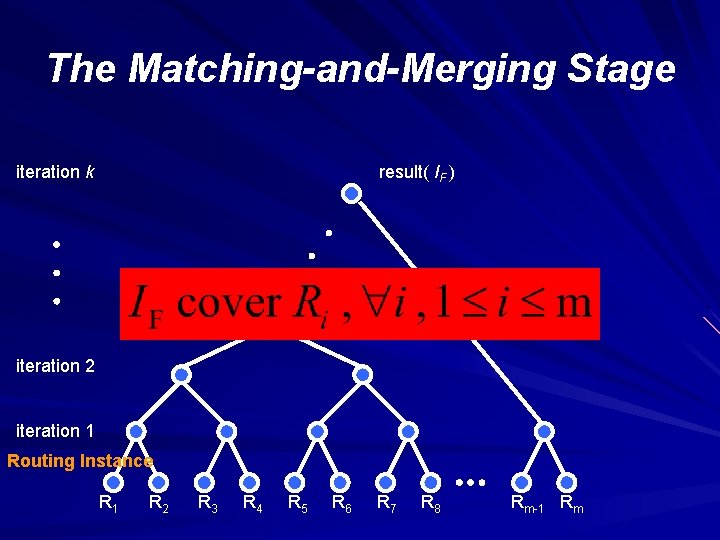
The Matching-and-Merging Stage iteration k result( IF ) iteration 2 iteration 1 Routing Instance R 1 R 2 R 3 R 4 R 5 R 6 R 7 R 8 Rm-1 Rm

Left-Edge Algorithm 1 2 3 4 5 6 7 8 9 10

The Tuning Stage Apply the basic left-edge algorithm to route the nets in IF Sort the resulting tracks in the nonincreasing order of their total lengths occupied by the nets The first T tracks are chosen
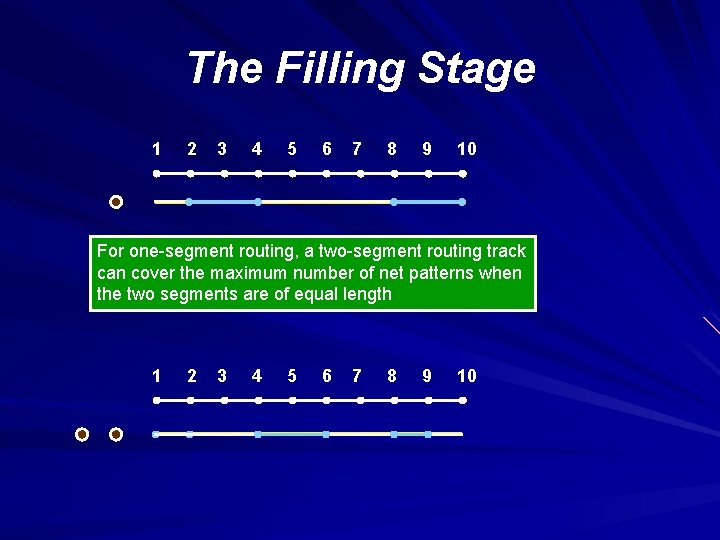
The Filling Stage 1 2 3 4 5 6 7 8 9 10 For one-segment routing, a two-segment routing track can cover the maximum number of net patterns when the two segments are of equal length 1 2 3 4 5 6 7 8 9 10

For K-segmentation Design Split each segment into K sections of equal length right after the aforementioned procedure

Experimental Results
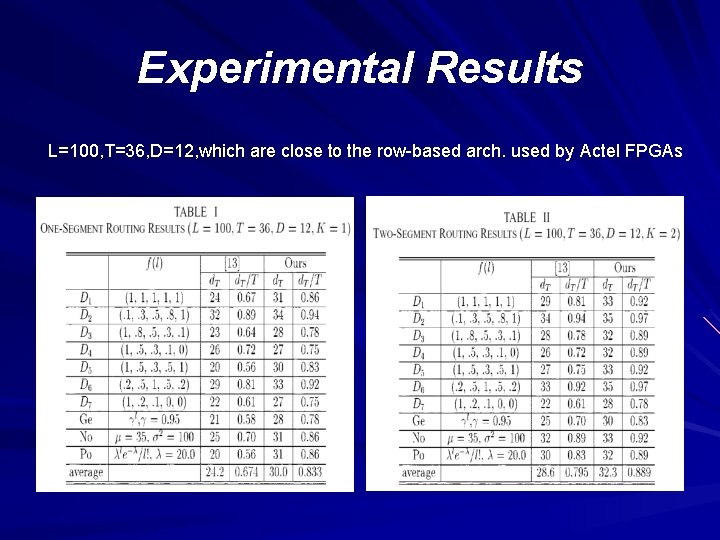
Experimental Results L=100, T=36, D=12, which are close to the row-based arch. used by Actel FPGAs

Experimental Results
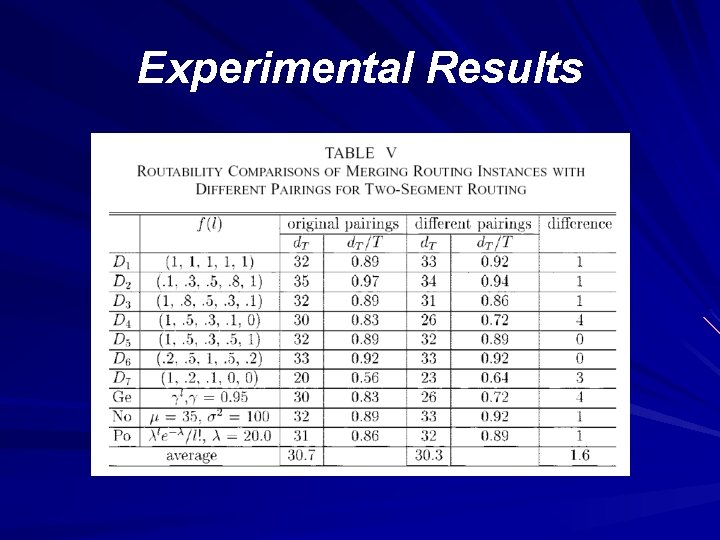
Experimental Results

Conclusion

Conclusion Present a new direction for studying FPGA segmentation design based on the graphmatching formulation Targeting at the optimal arch. directly is the major factor that leads to substantially better performance than previous works
- Slides: 23