Matching and Routing Structures and Algorithms Andrs Seb

Matching and Routing: Structures and Algorithms András Sebő, CNRS, IMAG-Leibniz, Grenoble

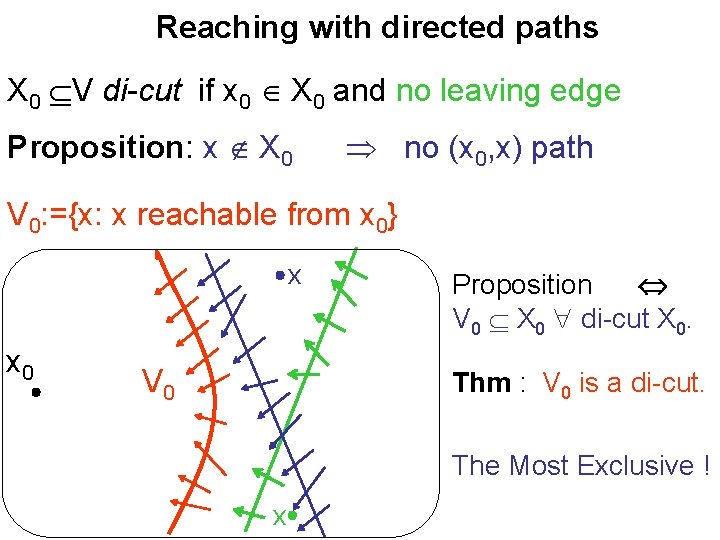
Reaching with directed paths X 0 V di-cut if x 0 X 0 and no leaving edge Proposition: x X 0 no (x 0, x) path V 0: ={x: x reachable from x 0} x x 0 V 0 Proposition V 0 X 0 di-cut X 0. Thm : V 0 is a di-cut. The Most Exclusive ! x

Bidirected Graphs Defined by Edmonds, Johnson (‘ 70) to handle a general class of integer linear programs containing matchings and their generalizations and tractable with the same methods. a bb {0, +1, -1, +2, -2}V , (a, b V, , b {-1, 1} ) + { a bb (x) = +b if x=a=b if x=a b, b if x=b a 0 if x {a, b} a - + + - - + b bidirected graph: G=(V, E), e E a, b, , b: e=a bb bidirected (a , bb) path : P E, e P e = a bb. Then bb (b) is reachable from a (a).

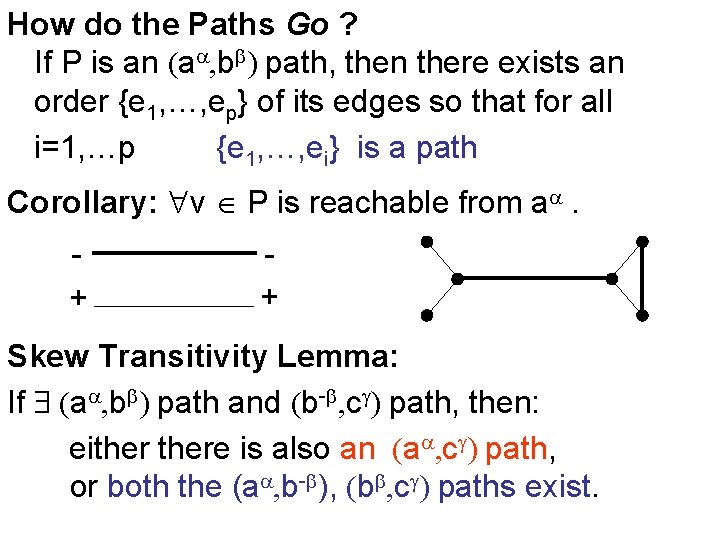
How do the Paths Go ? If P is an (a , bb) path, then there exists an order {e 1, …, ep} of its edges so that for all i=1, …p {e 1, …, ei} is a path Corollary: v P is reachable from a . + + Skew Transitivity Lemma: If (a , bb) path and (b-b, cg) path, then: eithere is also an (a , cg) path, or both the (a , b-b), (bb, cg) paths exist.

We proved in case x 0 V+ V- , eg, if d(x 0)=1 (i) x 0 V+ V(ii) V+ V- does not induce any useful edge. x 0’ (iii) For a component C of G - V+ Veither C V+ V- & 1 useful edge entering C. or C V+ = C V- = & 0 ‘’ x 0 - V+ V- x’ 0 - - ++ - + ‘’ V- V + - - - ‘’ ‘’

It follows immediately for the general case that: (i) x 0 V+ (ii) V+ V- does not induce any useful edge. x 0‘ (iii) For a component C of G - V+ Vx 0 + either C V V , x 0 C and 1 useful edge entering C, x 0 C and no “ “ “ or C V+ = C V- = and 0 useful ….

Remark: particular bidirected cuts (i) x 0 X+ X (ii) X: = X+ X- does not induce any useful edge. (iii) For a component C of G-X either C X+ X- & 1 useful edge entering C. or C X+ = C X- = and no “ “ “

Bidirected Cuts in General (X+ , X- ) , X+ , X- V is a bi-cut for x 0 -, if (i) x 0 X+ (ii) X: = X+ X- does not induce any useful edge. (iii) For a component C of G-X either C X+ X- , x 0 C and 1 useful edge entering C, x 0 C and no “ “ “ or C X+ = C X- =

What do bi-cuts exclude ? Proposition: If (X+ , X- ) is a bi-cut for x 0 , then x X+ there is no (x 0 - , x+) path, x X- there is no (x 0 - , x -) path. Proof : Choose x V, and P an (x 0 - , x) path, so that P is a counterexample, and P min … + + + X-X+ X X - - + - -- V+: ={v V: (x 0 - , v+) path}, V-: ={v V: (x 0 - , v -) path} Proposition V+ X+ , V- X- (X+ , X- ) bi-cut

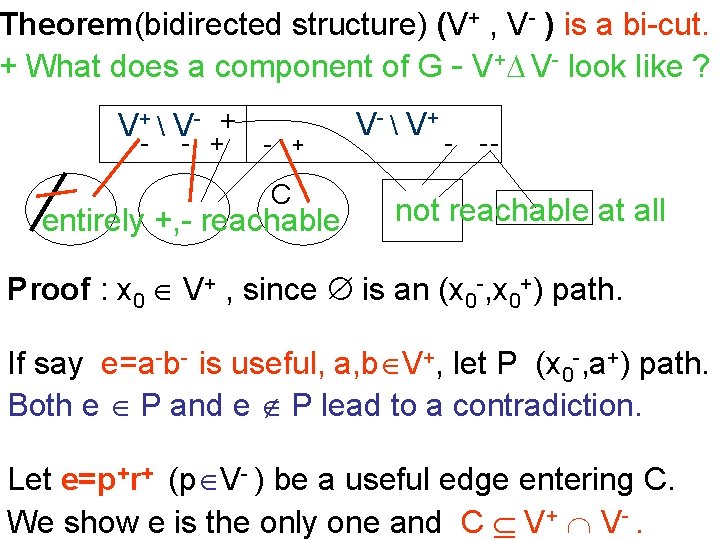
Theorem(bidirected structure) (V+ , V- ) is a bi-cut. + What does a component of G - V+ V- look like ? V+- V- - ++ - + C entirely +, - reachable V- V+ - -- not reachable at all Proof : x 0 V+ , since is an (x 0 -, x 0+) path. If say e=a-b- is useful, a, b V+, let P (x 0 -, a+) path. Both e P and e P lead to a contradiction. Let e=p+r+ (p V- ) be a useful edge entering C. We show e is the only one and C V+ V-.

trick: to switch the signs in a point does not change the accessibility of v V. V p + p’ + e + + r + Claim : V r-(C)= V r-(C) r’ Enough: : x Vr-+ (C), x V+ V - x V – If an (x 0 -, x-)-path enters last on x- + e : DONE If an (x 0 -, x-)-path enters last on p’r’: contradiction in either case of the Skew Transitivity Lemma.

(l, u)-factors (l u) + parity constraints in some vertices Find F E with minimum deficiency, where def : = {d. F(v) - u(v): d. F(v) > u(v)} + { l(v) - d. F(v): d. F(v) < l(v)} x 0 d. F < l : - u< d. F < l , u d. F < l , F d. F > u : + u< d. F l , F

Lemma: If one of the following statements hold, the F does not have minimum deficiency: a. x 0 V+ Vb. x V+: d. F(x)<u(x), and not d. F(x)+1=u(x)=l(x) c. x V- : d. F(x)> l(x), and not d. F(x) -1=u(x)=l(x) U: oversat OPT: V+ V - + - - + L: undersat - + u=l and+-1 (+ odd) V- V + - -- feasible Lovász’s structure theorem (containing Tutte’s existence theorem, Lovász’s minmax theorem for the deficiency): universal U, L is a ‘Tutte-set’.

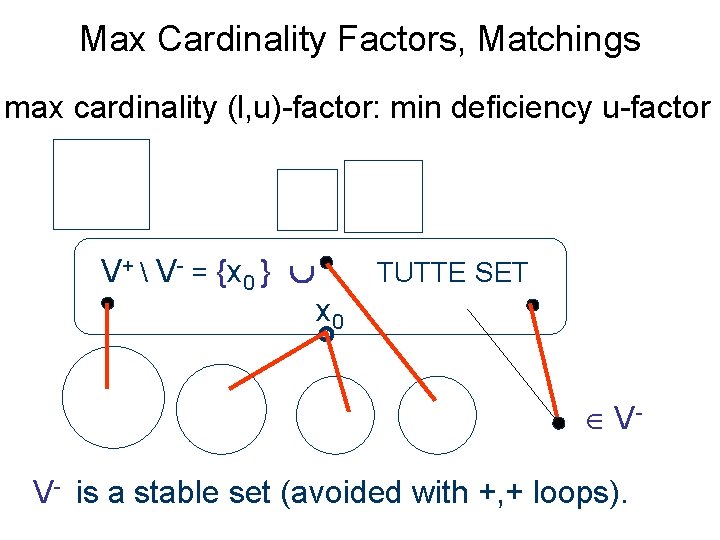
Max Cardinality Factors, Matchings max cardinality (l, u)-factor: min deficiency u-factor V+ V- = {x 0 } TUTTE SET x 0 V- V- is a stable set (avoided with +, + loops).

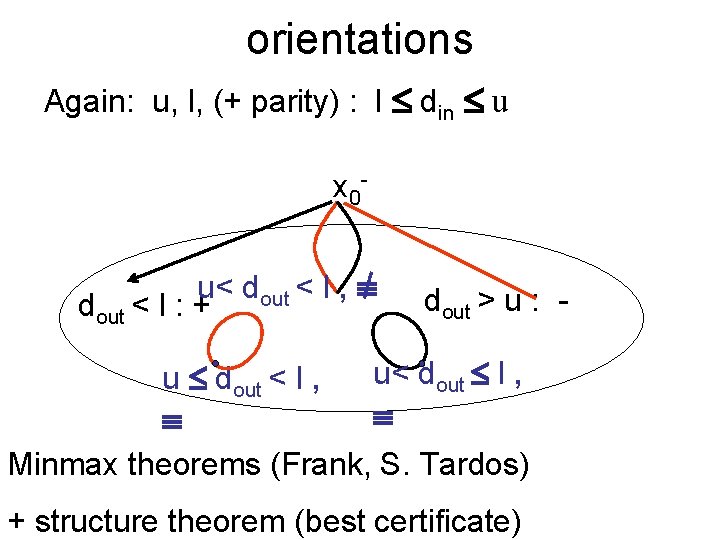
orientations Again: u, l, (+ parity) : l din u x 0 u< dout < l , dout < l : + u dout < l , dout > u : - u< dout l , Minmax theorems (Frank, S. Tardos) + structure theorem (best certificate)

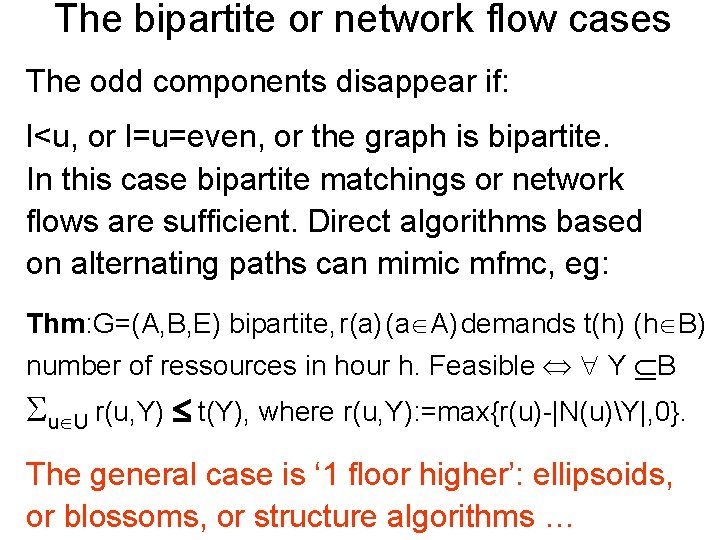
The bipartite or network flow cases The odd components disappear if: l<u, or l=u=even, or the graph is bipartite. In this case bipartite matchings or network flows are sufficient. Direct algorithms based on alternating paths can mimic mfmc, eg: Thm: G=(A, B, E) bipartite, r(a) (a A) demands t(h) (h B) number of ressources in hour h. Feasible Y B u U r(u, Y) t(Y), where r(u, Y): =max{r(u)-|N(u)Y|, 0}. The general case is ‘ 1 floor higher’: ellipsoids, or blossoms, or structure algorithms …

Solution of Exercises 9, 10 C(G)={x V(G): no red-red & no red-blue} A(G)={x V(G): no red-red & red-blue} Solution Exercise 9: V C(G) : red-red or red-blue red-red: {x V(G): M x is uncovered} =: D(G) additional red-blue : neighbors of D =A(G) (D neighbors of D) = V C(G)

Conclusion about bidirected graphs First, in terms of matchings: Exercise 8: If A is a Tutte set, then from x 0 - to x A there is no red-red alternating path - to x C, C even comp of G-A no red-red no red-blue C(G)={x V(G): no red-red & no red-blue} A(G)={x V(G): no red-red & red-blue}

Confusing: A(G) itself is not maximal among Tutte-sets A. (The reason is that it corresponds to V+ V- and not V+. ) Gallai-Edmonds : A(G) is a Tutte-set. Proof : (V+, V-) is a bidirected cut. S. of Exercise 10: C(G) is max among all C: triv A(G) C(G) is max among all A C (where A is a Tutte-set and C the of even) , because there is no red-red path to A C , and A(G) C(G) is the set of all such vertices.

Conclusion about bidirected graphs and the way they can be applied Thm : (V+, V-) is a bidirected cut. (most excl) This certifies that other vertices are not reachable. Algorithmic proof: (ii) is not satisfied: useful edge induced by X+ X(iii) ‘’ ‘’ ‘’ : two useful edges leaving a comp: new path by Skew Transitivity. Application: existence or max of subgraphs with constraints on degrees (bounds, parity, Orientation, etc. ) Proof of optimality: 1. ) Ex 11. 2. )minmax

x 0

x 0

Theorem: G bipartite, w: E {-1, 1}, cons. , x 0 V Then | l (u) – l (v) | = 1 for all uv E, and for all D D : d(D) contains 1 negative edge if x 0 D 0 0 negative edge if x 0 D Proof (Sketch): Induction with resp. to |V|. If l(b)=min {l(x) : x V} then Exercise 21 proves the statement for {b} D. Contract d(b). The graph remains cons, since if not, there is a 0 circuit through b with b , Apply Exercise 19, contradicting Exercise 21. ~Similarly, the distances do not change. Induction.

p integer function is a potential (with center x 0 ), if (i) p(x 0)=0 (ii) | p (u) – p (v) | = 1 for all uv E, conservat. (iii) for all D D(p) : d(D) contains and 0 1 negative edge if x 0 D 0 negative edge if x 0 D bound upper for the distances Algorithm: INPUT: G, w, x 0 TASK: Find the distances from x 0 While the distances do not form a potential find a better path or a negative circuit. (Ref: Finding …)

Applications Method for solving (in parallel + structure of ) : - Min (weighted) matchings - planar disjoint paths (+ planar max cut, via holes, air transport, Ising model) - the Chinese Postman problem - Minimizing T-joins, T-cuts (including min paths) - weighted algorithms for these, since they can mimic the +-1 bipartite case. ref: A. S. , Potentials in Undirected Graphs and Planar multiflows, SIAM J. Computing, March 1997, 582 -603

Answers: The algorithm that finds distances from x 0 is polynomial: O(n 4). It does not know about ‘efficient labelling’. Advantages: - it finds a potential, and The Best one, which helps in some applications to integer mflows. - the ‘classical’ algorithm reduces eg cardinality postman to weighted matchings. - helps in ‘reading’ matching th, and leads to generalizing it to conservative graphs (postman, planar disjoint paths, etc. ) – used eg for integer multiflows.

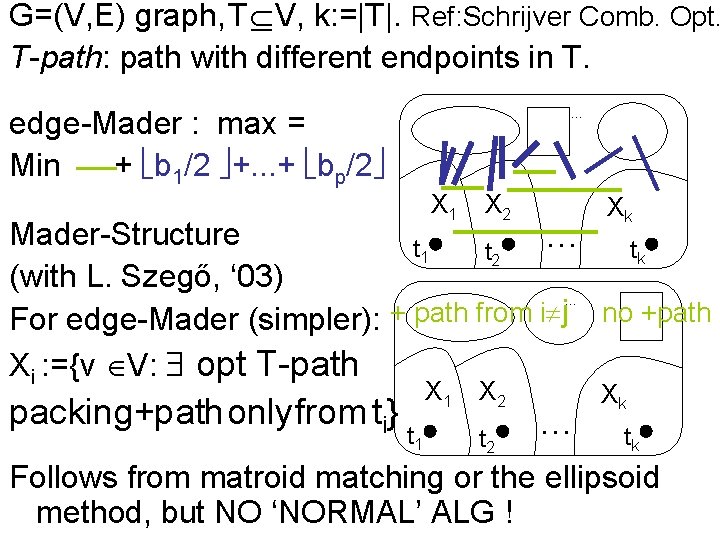
G=(V, E) graph, T V, k: =|T|. Ref: Schrijver Comb. Opt. T-path: path with different endpoints in T. edge-Mader : max = Min + b 1/2 +. . . + bp/2 … X 1 X 2 Xk Mader-Structure … tk t 1 t 2 (with L. Szegő, ‘ 03) For edge-Mader (simpler): + path from i j no +path Xi : ={v V: opt T-path … packing+path only from ti} X 1 t 1 X 2 t 2 … Xk tk Follows from matroid matching or the ellipsoid method, but NO ‘NORMAL’ ALG !

Jump systems A jump system (Bouchet, Cunnigham ’ 93) is a set of integer vectors J so that for every u, v J and step u+ei from u towards v, either u+ei J or there exists a step u+ei+ej J from u+ei towards J. Examples: matroid independent sets, bases. Degree sequences (B. C. ): you have a proof according to Exercise 12 ! The covered vertices of T-path packings (with M. Sadli using Schrijver’s (cf The Book) simple proof. Insight and generalization of results on graph factors: jump system intersection theorems. There are ‘holes’.