MAT 9 JA Metaheuristics 2 Evolutionary Strategies and

MAT 9 JA: Metaheuristics #2 Evolutionary Strategies and Genetic Algorithms Dr Jerry Swan Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 1

Population-Based Metaheuristics • In the previous lecture we looked at local search, e. g. hill climbing, simulated annealing, tabu search. – These techniques have a single current solution. • In this lecture, we take a look at population-based approaches. • These include: – Evolutionary Strategies – Genetic Algorithms – Genetic Programming Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 2

Population-Based Approaches • Rather than maintain a single candidate solution we maintain a population of them. The idea is that population members interact to promote good solutions. • Population-based approaches are loosely inspired by Darwinian evolution, which can be (roughly) characterized as ‘survival of the fittest ’: • An abstraction of real-world evolution… … real-world entities do not evolve in isolation – there are many competing/collaborating species (co-evolution). Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 3

Inspiration not Devotion • Claim that the emphasis should be on loosely inspired. • We may legitimately wish to be inspired by nature but we are not constrained by it: – “That’s not how the biology works. ” – “So what - it works!” (But why does it work? ? ) • But general benefits are to be had (and little is lost) by a more detailed investigation of natural mechanisms. Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 4

‘Inspired' Optimization • There is debate on the similarity between the abstractions of ‘bio-inspired’ optimization and the actual biological mechanisms that gave rise to them. • Biology is a rich domain and our abstractions necessarily simplify (e. g. some ants use (at least) seven different types of pheromones. . . ). • How much `useful machinery’ do we lose by using such simple models? We start by looking at Evolutionary Strategies (very simple) and move on to Genetic Algorithms (more complex). Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 5

Evolutionary Strategies Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 6

Evolutionary Strategies • Developed in 60 s and 70 s in Germany by Bienert, Rechenberg, and Schwefel. • Uses the evolutionary concept of randomized mutation. • Originated with numerical optimisation problems. • Traditionally works with real-valued vectors… … but can work with any solution representation for which we can define `mutation’. Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 7

Gaussian Mutation • For real-vectors, the mutation degree is typically drawn from a Normal (a. k. a. Gaussian) distribution: • Initially, N(0, 1) is used… Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 8

Real-valued Solution Representation x 1 xn Vector of real-valued fields 1 Real-valued evolutionary parameters x 1 xn 1 x’n ’ 1 Computing Science and Mathematics n MAT 9 JA: Metaheuristics #2 - 9 ’n

Mutating Solutions • Each field is mutated according to a Gaussian distribution (mean 0) with standard deviation . t t+1 x 1 xn N(0, 1) N(0, n) x’ 1 x’n Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 10

Basic ES • Has a single parent which gives rise to a single child by mutation. • The child is compared with parent and the best survives. • This essentially hill-climbing. • … except that the mutation rate is part of the ‘chromosome’ and the standard deviation of the mutation rate is updated too. . . Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 11

Schwefel's 1/5 Success Rule • Determine percentage ps of successful mutations in past k iterations. • Update each after every k iterations by = /c if ps > 1/5 = • c if ps < 1/5 = if ps = 1/5 where 0. 8 c 1 Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 12

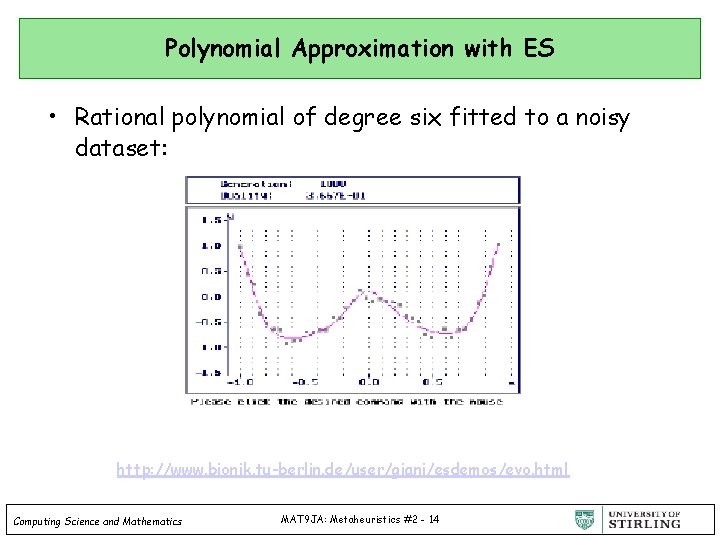
ES for Function Approximation • Given a set of data-points in the plane, fit a polynomial (or rational function) to these points, minimizing the error… Data Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 13

Polynomial Approximation with ES • Rational polynomial of degree six fitted to a noisy dataset: http: //www. bionik. tu-berlin. de/user/giani/esdemos/evo. html Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 14

But mutation is not the whole story. . . • More complex creatures create offspring by recombining their genetic material using crossover: • This is the essential additional feature of genetic algorithms. . . Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 15

Genetic Algorithms Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 16

Genetic Algorithms • Developed by John Holland in the 60 s and gaining wider publicity in the 70 s and 80 s. • Further developed by one of Holland’s student David Goldberg. • An extremely popular technique (10, 000 s of genetic algorithm papers). • Applied to a huge number of application domains. Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 17

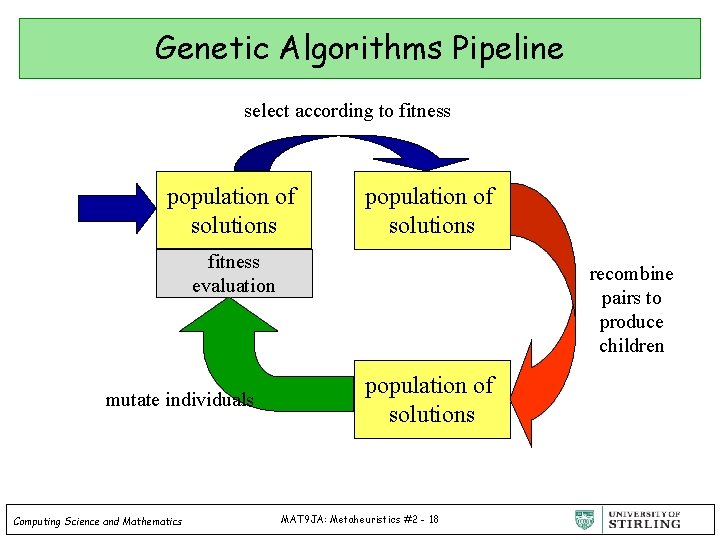
Genetic Algorithms Pipeline select according to fitness population of solutions fitness evaluation mutate individuals Computing Science and Mathematics recombine pairs to produce children population of solutions MAT 9 JA: Metaheuristics #2 - 18

GA Example - Simple Optimization Problem • Maximise f(x)=x over the interval [0, 15] • We will choose f(x) =x as the fitness value for candidate solution x. – Note: this is a choice. – No reason in principle why this should be used in preference to, say, x 2. – In general, the fitness function and the objective function need not be the same. Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 19

Representation • We will represent candidate solutions x as strings (chromosomes) of four bits. This is the genotype – it is the genotype that is subject to genetic operations. • We interpret a bit string as the non-negative decimal integer for which it naturally encodes. This is the phenotype. Chromosome with bi in {0, 1} b 3 b 2 b 1 b 0 Interpretation 23 b 3 + 22 b 2 + 21 b 1 + 20 b 0 0000=>0, 0001=>1, …, 1110=14, 1111=15 Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 20

Initial Population • For this very simple example we will use a population size M=4. These are generated randomly…. . a 0 0 1 0 0 4 b 0 0 0 1 1 3 c 0 0 0 1 1 3 d 0 0 0 1 0 2 12 Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 21 Total pop fitness

Selection • Select probabilistically according to fitness (b 0) a 1 0 0 1 1 3 (a 0) b 1 0 0 4 (a 0) c 1 0 0 4 (c 0) d 1 0 0 1 1 3 14 Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 22 Total pop fitness

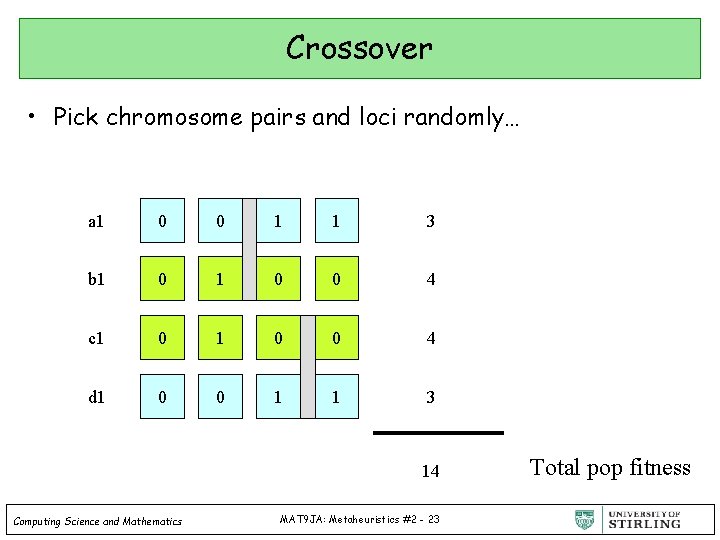
Crossover • Pick chromosome pairs and loci randomly… a 1 0 0 1 1 3 b 1 0 0 4 c 1 0 0 4 d 1 0 0 1 1 3 14 Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 23 Total pop fitness

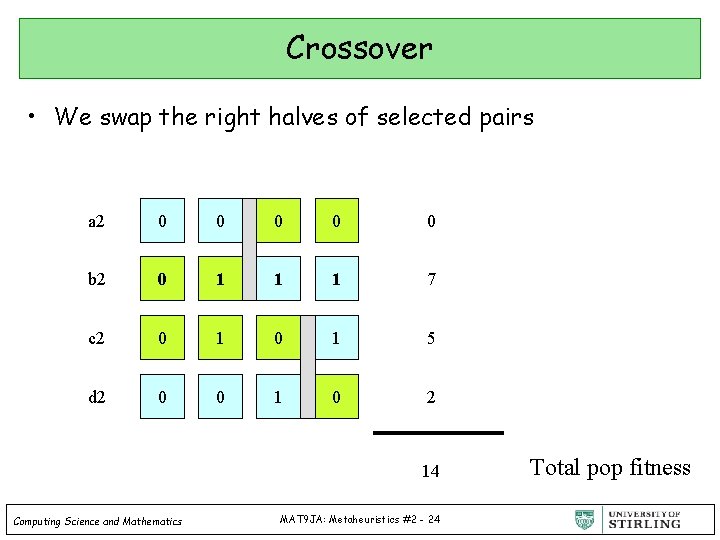
Crossover • We swap the right halves of selected pairs a 2 0 0 0 b 2 0 1 1 1 7 c 2 0 1 5 d 2 0 0 1 0 2 14 Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 24 Total pop fitness

Mutation • With small probability mutate (here flip the bit) each gene value. Here we get very lucky…. . a 0 0 0 b 0 1 1 1 7 c 0 1 5 d 1 0 10 22 Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 25 Total pop fitness

… and repeat … • Can easily see why repeating this general process will give rise eventually to a solution 1111=>15 • The process is repeated until a satisfactory outcome is achieved, or else we run out of time. Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 26

Representation Issues • Representation is an important modeling step. • Here the representation and interpretation are very natural. • What if we wanted to maximize over the interval [0, 12]? – We could interpret each bit string as an integer mod 13. – This introduces a bias since the number of chromosomes that encode for each integer in this range varies: • 0 is encoded by 0000 and 1101 • 1 is encoded by 0001 and 1110 • 2 is encoded by 0010 and 1111 • The rest are encoded by the single binary representation. Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 27

Roulette wheel: Proportional Selection • Chromosomes are selected with probability proportional to their fitness. Often referred to as roulette wheel selection. • Some problems with this approach… Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 28

Issues with Proportional Selection • If the objective function takes negative values you need to be careful! – Scaling is an option… • If one solution is much better than the rest, this cause the population to stagnate and the GA to get trapped in a local minimum. • Some popular alternative selection schemes are… Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 29

Rank Selection • Form a list of population members, ranked according to fitness. • Now select probabilistically with probability: • The sum of the ranks k is 1+2+…+M = M(M+1)/2 • There are many variations on this theme… Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 30

Tournament Selection • Generate a permutation of the population members – essentially gives a list. • Look at successive blocks of k members and select the fittest – this is the tournament winner. • Repeat using further permutations until M parents have been selected. Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 31

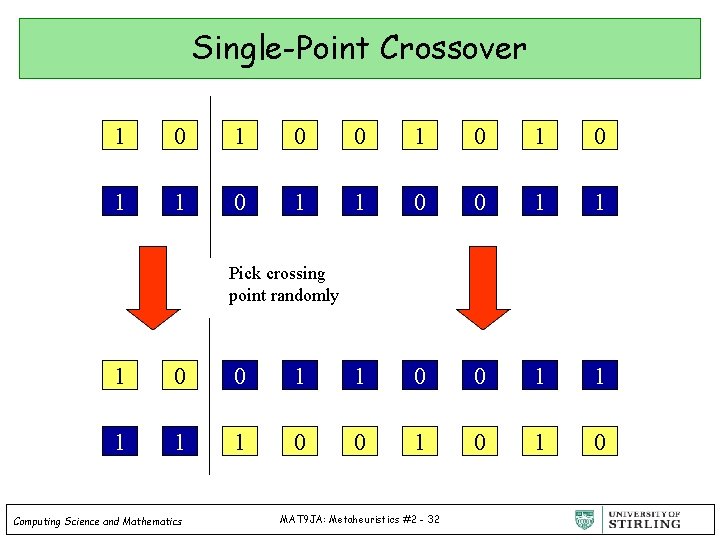
Single-Point Crossover 1 0 0 1 0 1 1 0 0 1 1 Pick crossing point randomly 1 0 0 1 1 1 0 0 1 0 Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 32

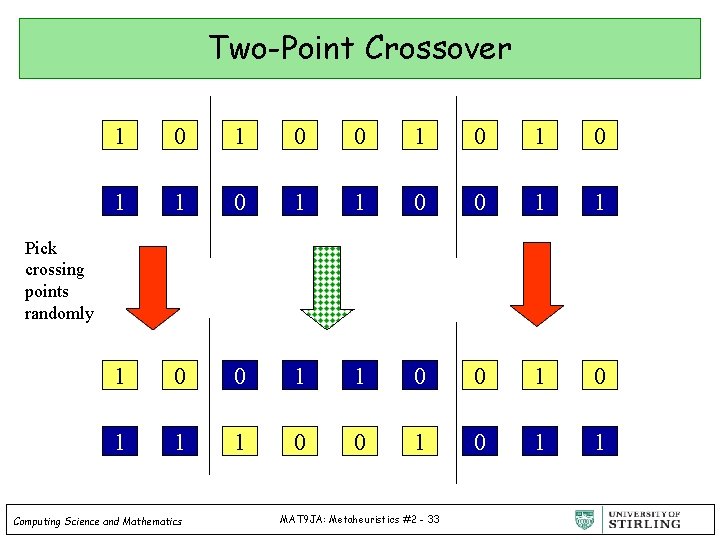
Two-Point Crossover 1 0 0 1 0 1 1 0 0 1 0 1 1 1 0 0 1 1 Pick crossing points randomly Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 33

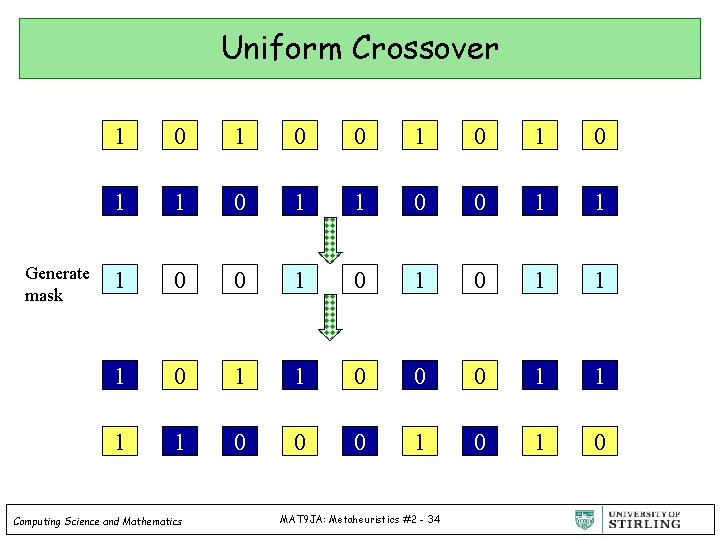
Uniform Crossover Generate mask 1 0 0 1 0 1 1 0 0 1 0 1 1 1 0 0 0 1 0 Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 34

Some Other Issues with GAs. . . • Choice of parameters: – Population size (De. Jong) – Initialization method. . . – Crossover rate – Mutation rate – Selection operator • Choice of fitness functions – the choice matters a lot. • The new few slides discuss some other issues. . . Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 35

Crossover issue: disruption • Crossover can be highly disruptive: high-performing schema may not be preserved under crossover. • If solutions need to obey constraints, these may not be preserved under crossover. • Some options: – Arrange representation and operators so that a solutions are always valid. – Carry out a ‘repair’ operation on chromosomes to restore validity. Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 36

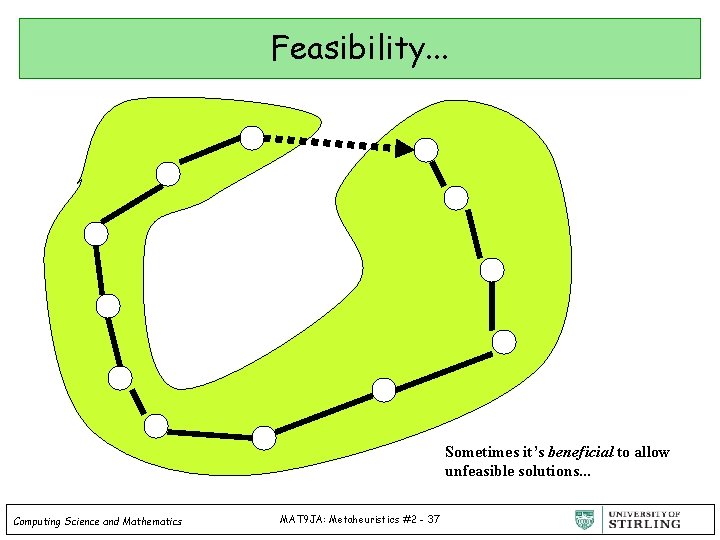
Feasibility. . . Sometimes it’s beneficial to allow unfeasible solutions. . . Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 37

Genotypes and Semantic Equivalence • Radically different genotypes may actually map to the same phenotype. • This may mean that recombining high-performing solutions result in radically-poorer children (despite in some sense being the “same” solution). Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 38

Question. . . • For a great many different types of problem, genetic algorithms work rather well… • Why do you think this is so? Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 39

Acknowledgements Thanks to John Clark for making his original slides available. Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 40

References Sean Luke, “Essentials of Metaheuristics” Freely downloadable from: http: //cs. gmu. edu/~sean/book/metaheuristics/Essentials. pdf Computing Science and Mathematics MAT 9 JA: Metaheuristics #2 - 41