MAT 4830 Mathematical Modeling Section 1 3 Conditional

Questions l What is the purpose of a conditional statement?

Questions l Describe a conditional statement in Maple.

Starting Next Monday l l You will be writing codes without an example that

Preview l l l Review Poisson Distribution Introduces the conditional statements Allow the flow

Example 0 On average, random customers per hour come into a local Starbucks during

Idea: Approximate the scenario by a binomial model l

Team Homework #1 l Use the definition of expected value and the Taylor expansion

Team Homework #2 A newsboy sells newspapers outside Grand Central Station. He has on

Example 1 l Consider the piecewise defined function l For each interval, we need

Example 1 l Consider the piecewise defined function For each interval, we need a

Example 1 Version 1 > fun(-2); fun(2); 4 2

Structure of the if-block Statements executed only if the condition is met. Otherwise, the

Example 1 Version 2 > fun(-2); fun(2); 4 2

Structure of the if-block There are two cases separated by one condition: the condition

Example 2 > fun(-3); fun(1); fun(3); -14 3 5 e(-1)

Homework l Read 1. 6 formatting with printf • We will not go into

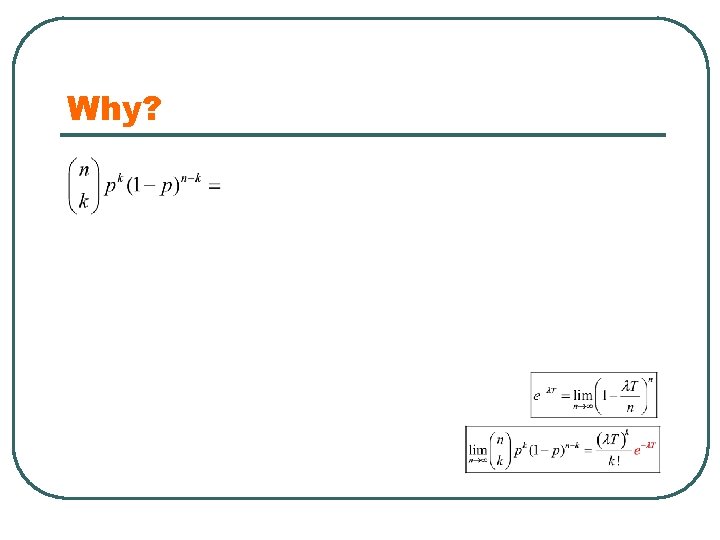
Slides: 31

Download presentation

MAT 4830 Mathematical Modeling Section 1. 3 Conditional Statements http: //myhome. spu. edu/lauw

Questions l What is the purpose of a conditional statement?

Questions l Describe a conditional statement in Maple.

Starting Next Monday l l You will be writing codes without an example that you can just modify on. You need to be able to write complete Maple programs on your own. No two should sit next to each other today. Learn to debug your own program is an important learning process.

Preview l l l Review Poisson Distribution Introduces the conditional statements Allow the flow of control to branch into two or more sections of codes based on the truth values of a control expressions

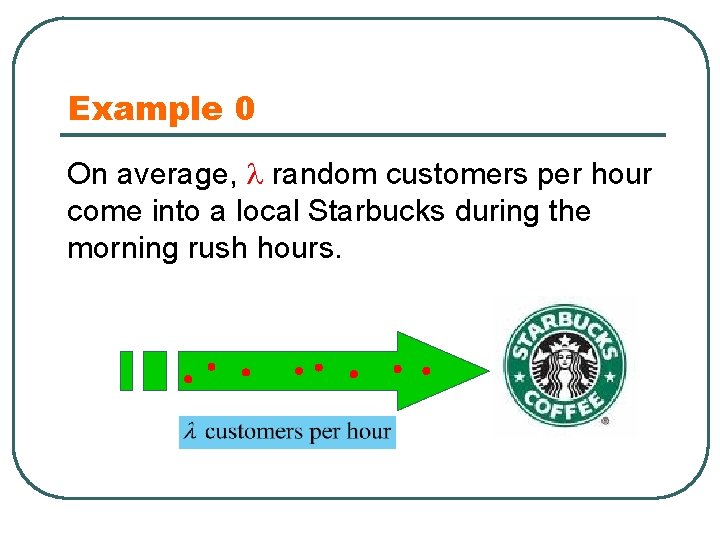
Example 0 On average, random customers per hour come into a local Starbucks during the morning rush hours.

Example 0 l

Idea: Approximate the scenario by a binomial model l

Idea: Approximate by a binomial model l

Theorem 1

Why? Calculus Formula:

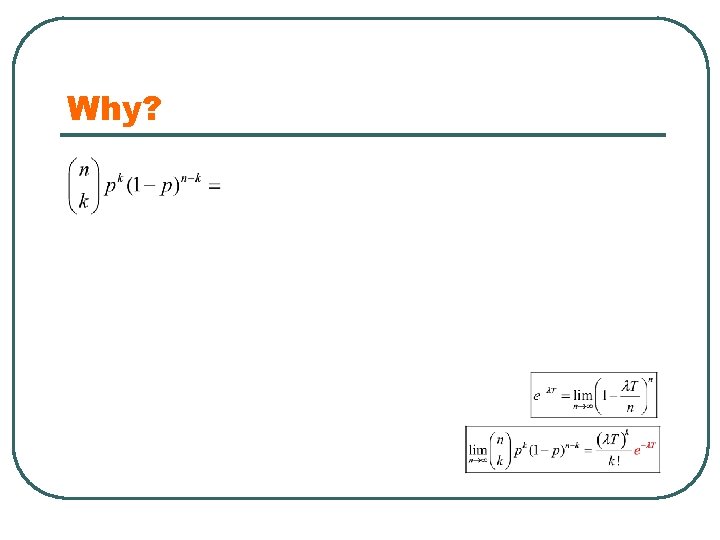
Why?

Team HW#1

Team Homework #1 l Use the definition of expected value and the Taylor expansion l Do not use the moment generating function.

Poisson Distribution l

Team Homework #2 A newsboy sells newspapers outside Grand Central Station. He has on average 100 customers per day. He buys papers for 50 cents each, sells them for 75 cents each, but cannot return unsold papers for a refund. How many papers should he buy? To maximize the expected profit

Zeng Section 1. 3

Example 1 l Consider the piecewise defined function l For each interval, we need a different formula to compute the function values

Example 1 l Consider the piecewise defined function For each interval, we need a different formula to compute the function values Q: Input=? , Output=? l

Example 1 Version 1

Example 1 Version 1 > fun(-2); fun(2); 4 2

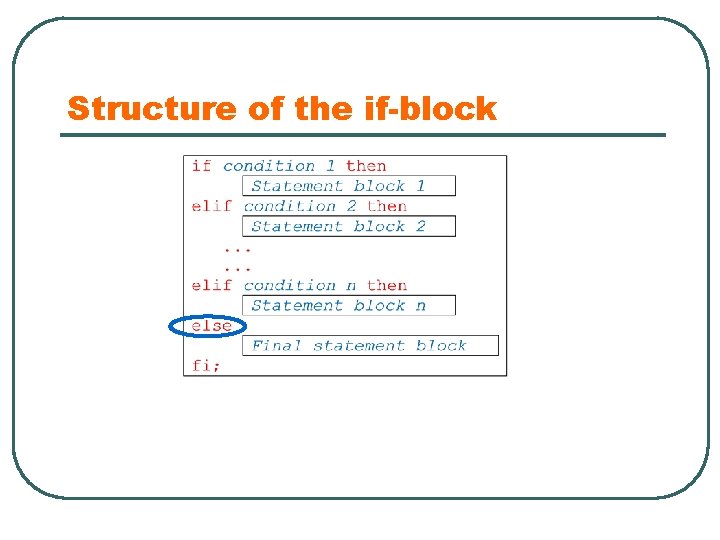
Structure of the if-block Statements executed only if the condition is met. Otherwise, the statements will be skipped:

Example 1 Version 2

Example 1 Version 2 > fun(-2); fun(2); 4 2

Structure of the if-block There are two cases separated by one condition: the condition is met or else:

Example 2 l We need 3 branches

Example 2

Example 2 > fun(-3); fun(1); fun(3); -14 3 5 e(-1)

Structure of the if-block

Homework l Read 1. 6 formatting with printf • We will not go into this section during lecture • You are expected to know how to use printf l See webpage