MAT 4830 Mathematical Modeling 4 1 Background on

MAT 4830 Mathematical Modeling 4. 1 Background on DNA http: //myhome. spu. edu/lauw

Remarks l l No handouts Need to read the textbook for more info All individual HW for this chapter (4. 14. 6) Techniques learned can be apply to other applications

Disclaimer l l l This is not a biology class! I do not know too much biology. We will ignore all possible theological questions and implications.

Our Learning Philosophy l l Acquire minimum background to start the analysis/ modeling. Ignore the complexity of the biochemical process.

Our Learning Philosophy l l Concentrate on certain mathematical problems. Very interesting problems once we get through the terminologies.

DNA l Genetic info is encoded by DNA molecules, which are passed from parent to offspring.
Bases 4 types of smaller molecules: Adenine (A), Guanine (G) Cytosine (C), Thymine (T)

Bases 4 types of smaller molecules: Adenine (A), Guanine (G) Purine Cytosine (C), Thymine (T) Pyrimidine
Bases A always pairs with T G always pairs with C

Bases A always pairs with T G always pairs with C Sequence: Complementary Sequence: AGCGCT TCGCGA
Bases l In order to describe a DNA, it suffices to list the bases in one strand.

Mutations l Mutations of DNA occur (randomly) from parent to offspring.

Mutations l Mutations of DNA occur (randomly) from parent to offspring.
Base Substitution l l A common form of mutation. A base is replaced by another base.

Base Substitution l l Transition: Pur by Pur, Pyr By Pyr Transversion: Pur By Pyr, Pyr By Pur

Basic Question l How to deduce the amount of mutations during the descent of the DNA sequences?
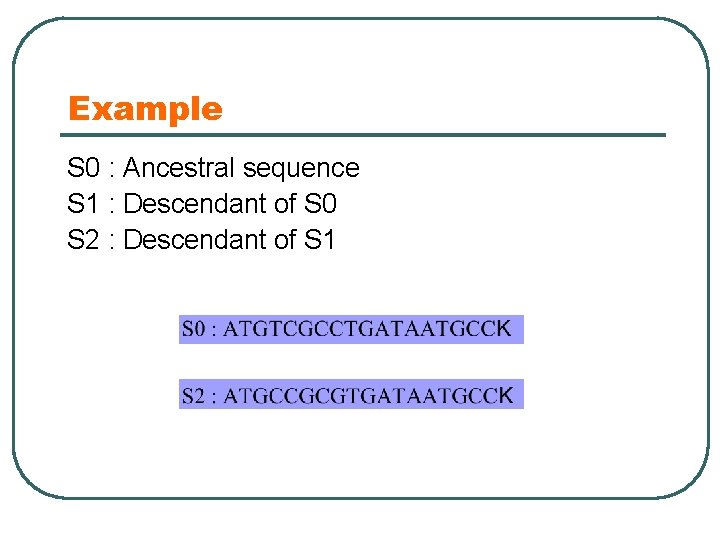
Example S 0 : Ancestral sequence S 1 : Descendant of S 0 S 2 : Descendant of S 1
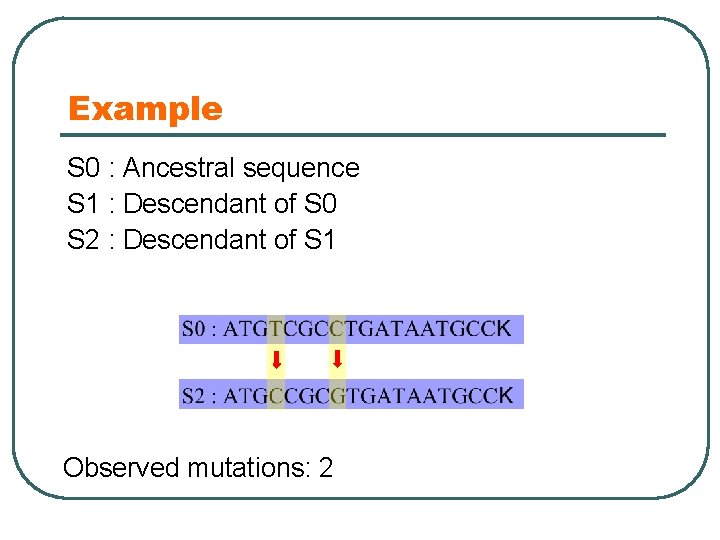
Example S 0 : Ancestral sequence S 1 : Descendant of S 0 S 2 : Descendant of S 1 Observed mutations: 2
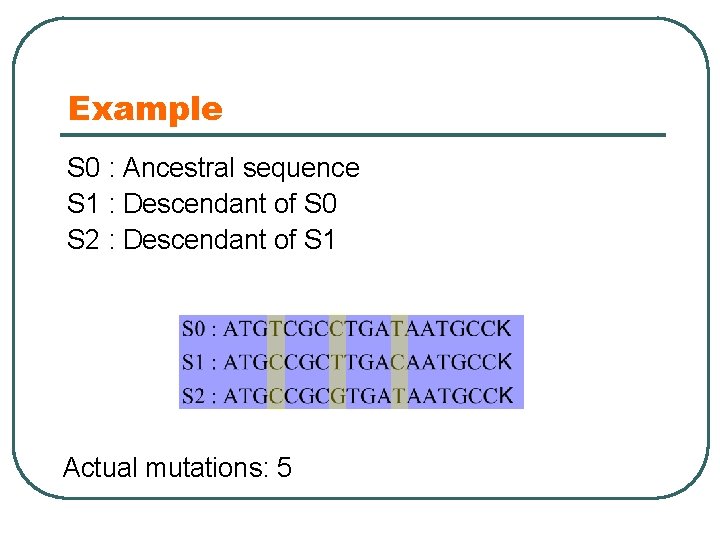
Example S 0 : Ancestral sequence S 1 : Descendant of S 0 S 2 : Descendant of S 1 Actual mutations: 5
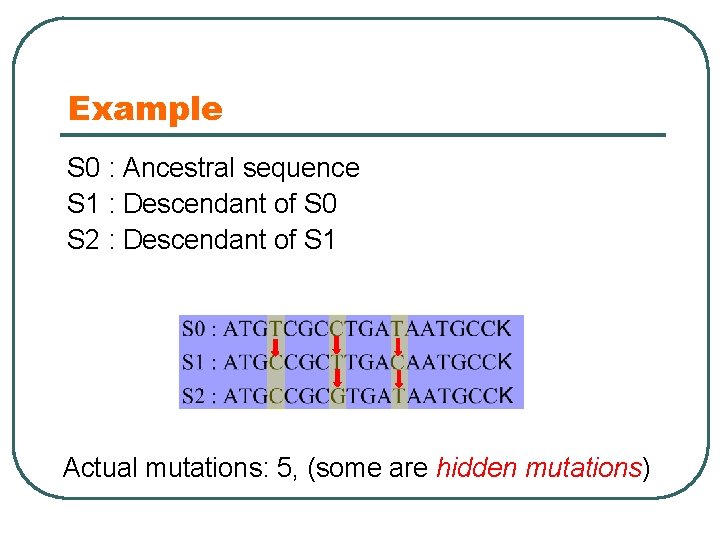
Example S 0 : Ancestral sequence S 1 : Descendant of S 0 S 2 : Descendant of S 1 Actual mutations: 5, (some are hidden mutations)

What Do We Want? l l Compare the initial and final DNA sequences Develop mathematical models to reconstruct the number of mutations likely to have occurred.

Reality… l l Seldom do we actually have an ancestral DNA sequence, much less several from different times along a line of descent. Instead, we have sequences from several currently living descendants, but no direct information about any of their ancestors.

Reality… l When we compare two sequences, and imagine the mutation process that produced them, the sequence of their most recent common ancestor, from which they both evolved, is unknown.

Orthologous Sequences l l Given a DNA sequence from some organism, there are good search algorithms to find similar sequences for other organisms in DNA databases. If a gene has been identified for one organism, we can quickly locate likely candidate sequences for similar genes in related organisms.

Orthologous Sequences l If the genes has similar function, we can reasonably assume the sequences are descended from a common ancestral sequence (orthologous)

Assumption l All sequences in our discussions are aligned orthologous DNA sequences

4. 2 An Introduction to Probability l Read Section 4. 2 to “review”.

4. 3 Conditional Probability l Read Section 4. 3 to “review”

Definition l

Example Suppose a 40 -base ancestral and descendent DNA sequences are

Example Count the frequency of base substitutions.

Example We can estimate

Example We can estimate

Example Q 1: What is the sum of the 16 numbers in the table? Why?

Example Q 2: What is the meaning of a row sum in the table?

Example We can form a table of conditional probabilities

Example Q 3: What is the sum of the entries in any column of this new table? Why?

Example Q 4: If instead of dividing by column sums, you divided by row sums, would you get the same results? What conditional probabilities would you be calculating?
- Slides: 38