MAT 360 Lecture 3 Models and Incidence geometry

MAT 360 Lecture 3 Models and Incidence geometry

Homework due next Tuesday n n n Translate Prop. 2. 2 and 2. 3 to “Shash geometry” and prove them (in “Shash words” Exercise 6 (Only Prop 2. 1, 2. 4 and 2. 5) Exercises 7 and 8.

Midterm n n Oct 25 th After that we will have one or two classes in the Math Sync site with the Geometer’s Sketchpad.

Incidence Geometry: Undefined terms n n n point line incident 4

Incidence Geometry: Axioms 1. For each point P and for each point Q not equal to P there exists a unique line incident with P and Q. 2. For every line T there exist at least two distinct points incident with T. 3. There exist three distinct points with the property that no line is incident with all the three of them.

Two Propositions of Incident Geometry n n If T and R are distinct lines that there are not parallel exists a unique point incident with both of them. There exist three distinct lines that are not incident with the same point.

Shash Geometry: Undefined terms 1. Kem 2. Tam 3. Shash

Shash Geometry: Axioms 1. For each kem P and for each kem Q not equal to P there exists a unique tam shash with P and Q. 2. For every tam T there exist at least two distinct kems shash with T. 3. There exist three distinct kems with the property that no tam is shash with all the three of them.

Definition n Two tams are squeezed if there is not kem shashing with both of them

Proposition 1: Dare to prove it! n Let T and R are distinct tams that are not squeezed. Then there is a unique kem shashing with both of them.

Proposition 2 n There exist three distinct tams that are not shashed with the same kem.

Definition n An interpretation of an given axiomatic system is a “dictionary” that assigns to each of the undefined terms of the axiomatic system a particular meaning.

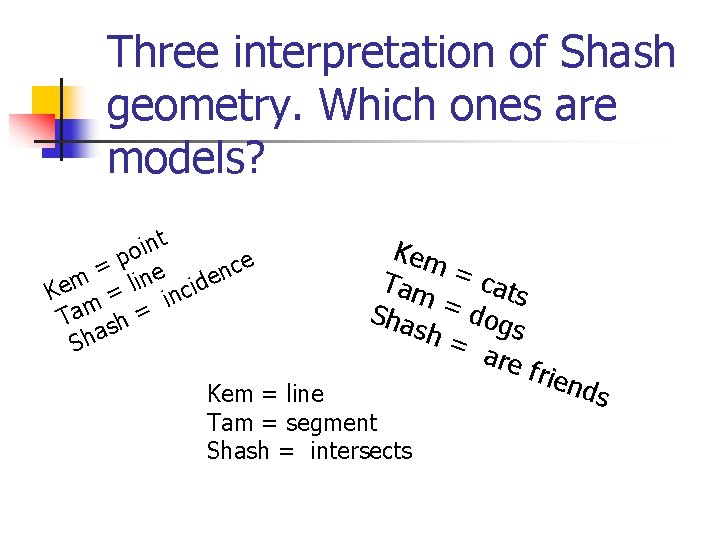
EXAMPLE n We can interpret the axioms of Shash geometry as n n n Kem = cats Tam = dogs Shash = are friends

Friendly Pets Geometry: Axioms 1. For each cat P and for each cat Q not equal to P there exists a unique dog friend with P and Q. 2. For every dog T there exist at least two distinct cats friend with T. 3. There exist three distinct cats with the property that no dog is friend with all the three of them.

Exercise n Translate Proposition 1 of Shash geometry to Friendly Pets geometry.

EXAMPLE n We can interpret the axioms of Shash geometry as Kem = line n Tam = segment n Shash = intersects Let’s call this interpretation “strange geometry”. n

EXERCISE n n Study the shash axioms with this interpretation. Are they correct statements? Can you use the answer you gave in the previous question to study the Propositions of the Shash Geometry proved ?

Strange Geometry: Axioms “Interpreted” 1. For each line P and for each line Q not equal to P there exists a unique segment intersecting with P and Q. 2. For every segment T there exist at least two distinct lines intersecting with T. 3. There exist three distinct lines with the property that no segment intersects all the three of them.

EXAMPLE n We can interpret the axioms of Shash geometry as n n n Kem = point Tam = line Shash = incidence Squeezed = parallel NOTE: We are using the “concrete” meaning of point, line and incidence here.

EXERCISE n n Study the shash axioms with this interpretation. Are they correct statements? Can you use the answer you gave in the previous question to study the Propositions of the Shash Geometry proved ?

Definition n An interpretation of the undefined terms of an axiomatic system for which the interpreted axioms become correct statements is called a model.

Three interpretation of Shash geometry. Which ones are models? t n i o p e c = ne n e m i d l i e c K = in m Ta sh = Sha Kem Tam = cats Sha = dog sh = s are fr Kem = line Tam = segment Shash = intersects iend s

A small change of direction n Now that we have played enough with shash geometry, we are going back to the usual formulation. So from now on, our undefined terms are points, lines and incidence (but keep in mind that we could be calling them kems, tams and shash)

Three letter interpretation n n Consider the set {A, B, C} Points: A, B and C Lines: {A, B}, {B, C}, {C, A} Incidence: “it is a member of” or “contains” Is this interpretation a model of Incidence Geometry Axioms?

“Usual plane” interpretation n Consider a plane P Points: “usual” points on P Lines: “usual” lines on P Incidence: “it is a member of” or “contains” n Is this interpretation a model? n n n

Observations: Given an axiomatic system. n n All the statements deduced from the axioms are correct statements of a model. If there exists a statement that does not hold in one model, then the statement cannot follow from the axioms.

EXERCISE n Consider Euclid fifth postulate, n n n “For every line l and every point P not in l there exist a unique line through P parallel to l. ” Is it a correct statement in the “three letter” model of the Incidence Axioms? Is it a correct statement in the “usual plane” model of the Incidence Axioms?

Definition: Given an axiomatic system, n A statement (in the language of the system) is independent of the if neither the statement or its negation can be proved from the axioms.

Observation, Given an axiomatic system n A statement that holds in one model and does not hold in another model is independent.

EXERCISE 1. Justify the previous observation. 2. Can you give an example of an independent statement of an axiom system?

Question When are two models isomorphic? (and what do we mean by “isomorphic”) n

Definition n Two models are isomorphic if there exists a one-to-one correspondence between the interpretation of each set of undefined terms, such that any relationship between the objects corresponding to undefined terms in one model is preserved, under the correspondence, in the second model.

Example: Construct an isomorphism between the models n n n Points: A, B and C Lines: {A, B}, {B, C}, {C, A} Incidence: set membership Points: {a, b}, {a, c}, {b, c} n. Lines: a, b, c n. Incidence: set membership. n

An axiom system is called n n n complete if there are not independent statements. consistent if it is impossible to deduce from the axioms a contradiction. categorical if all the models for the system are isomorphic.

Exercise: Is the Incidence Axiom System n n n complete? consistent? categorical?

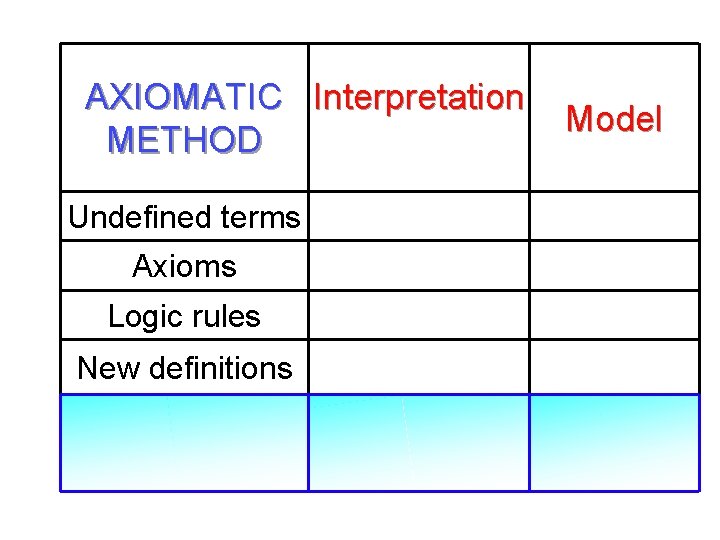
AXIOMATIC Interpretation METHOD Undefined terms Axioms Logic rules New definitions Model

Find a model of the following axiom system 1. For each point P and for each point Q not equal to P there exists a unique line incident with P and Q. 2. For every line T there exist at least two distinct points incident with T. 3. There exist three distinct points with the property that no line is incident with all the three of them. 4. There exist exactly three points.

Is the previous axiom system. . . n n n complete? categorical? consistent? 38

Find a model of the following axiom system 1. For each point P and for each point Q not equal to P there exists a unique line incident with P and Q. 2. For every line T there exist at least two distinct points incident with T. 3. There exist three distinct points with the property that no line is incident with all the three of them. 4. There exist exactly four points.

Is the previous axiom system. . . n n n complete? categorical? consistent? 40