MAT 2720 Discrete Mathematics Section 6 2 Permutations
















- Slides: 24

MAT 2720 Discrete Mathematics Section 6. 2 Permutations and Combinations http: //myhome. spu. edu/lauw

Goals l Permutations and Combinations • Definitions • Formulas • Binomial Coefficients

Permutations

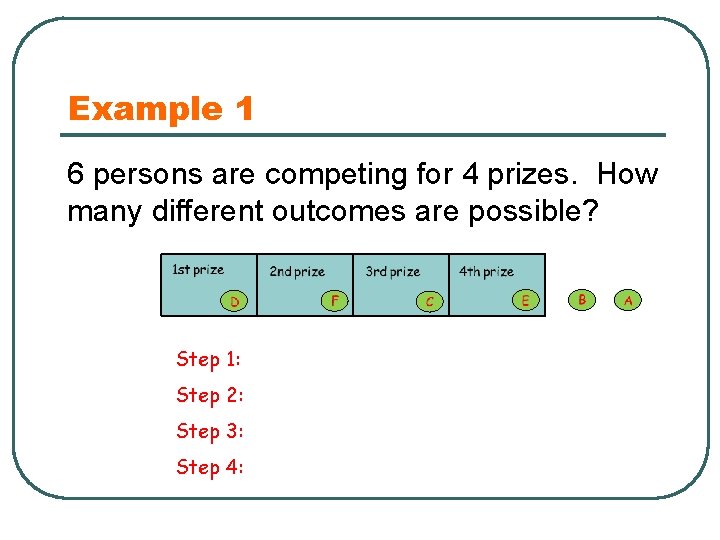
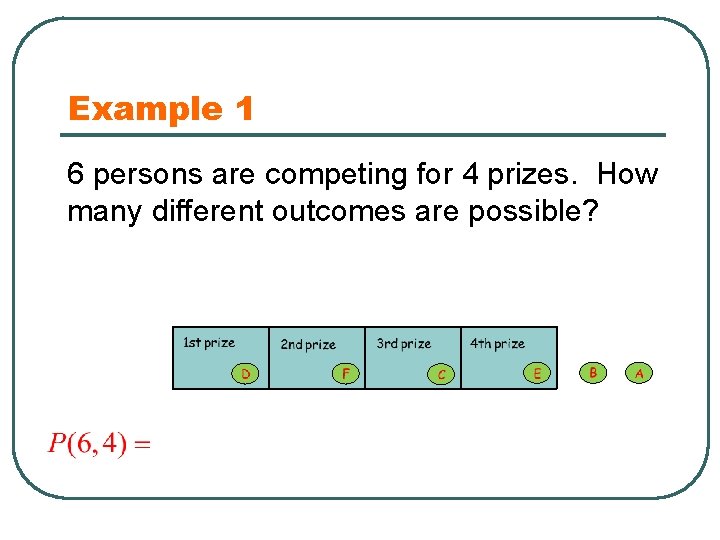
Example 1 6 persons are competing for 4 prizes. How many different outcomes are possible? Step 1: Step 2: Step 3: Step 4:

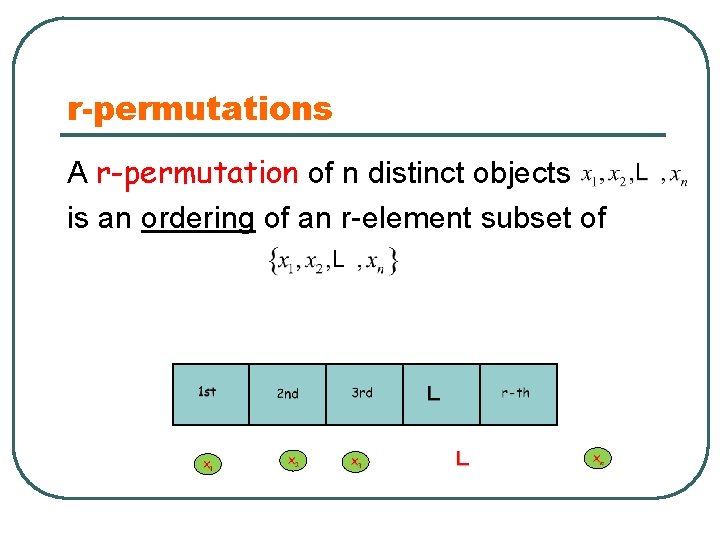
r-permutations A r-permutation of n distinct objects is an ordering of an r-element subset of

r-permutations A r-permutation of n distinct objects is an ordering of an r-element subset of The number of all possible ordering:

Example 1 6 persons are competing for 4 prizes. How many different outcomes are possible?

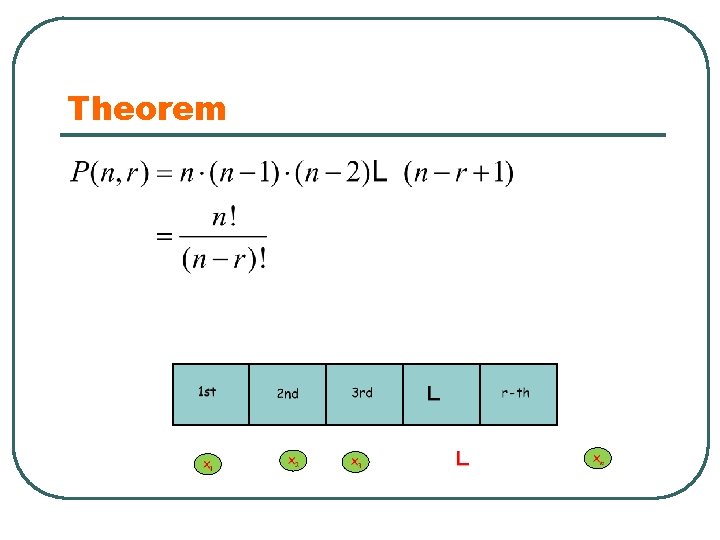
Theorem

Example 2 100 persons enter into a contest. How many possible ways to select the 1 st, 2 nd, and 3 rd prize winner?

Example 3(a) How many 3 -permutations of the letters A, B, C , D, E, and F are possible?

Example 3(b) How many permutations of the letters A, B, C , D, E, and F are possible. Note that, “permutations” means “ 6 permutations”.

Example 3(c) How many permutations of the letters A, B, C , D, E, and F contains the substring DEF?

Example 3(d) How many permutations of the letters A, B, C , D, E, and F contains the letters D, E, and F together in any order?

Combinations l l You probably have seen this formula before. One of the goals here is to explain to you why the formula you have learned in other classes is correct.

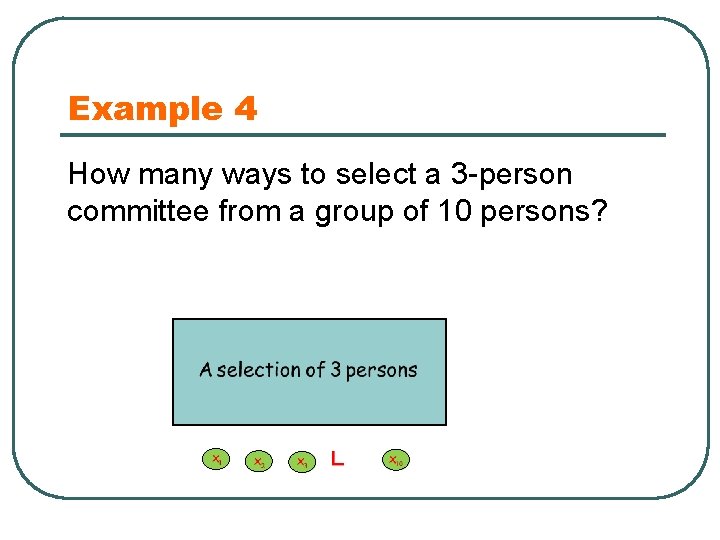
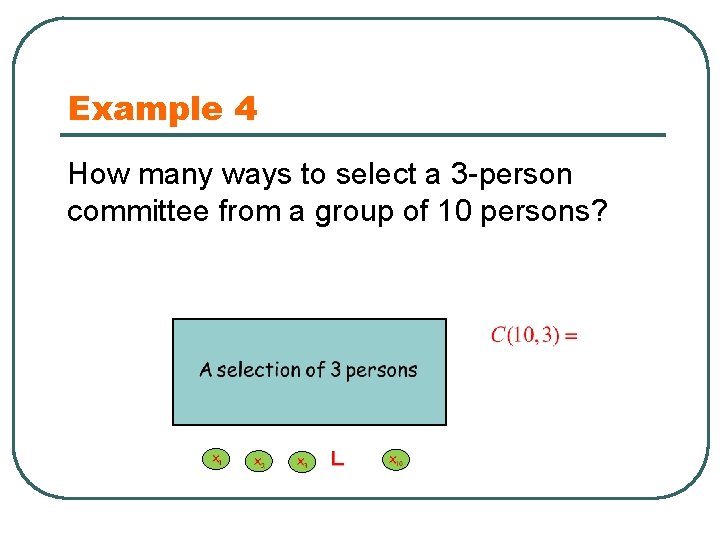
Example 4 How many ways to select a 3 -person committee from a group of 10 persons?

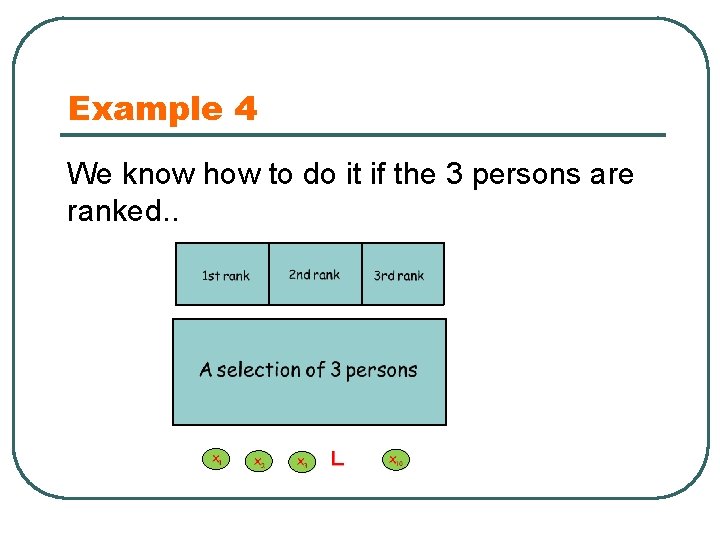
Example 4 We know how to do it if the 3 persons are ranked. .

r-combinations A r-combination of n distinct objects is an unordered selection of an r-element subset of

r-combinations A r-combination of n distinct objects is an unordered selection of an r-element subset of The number of all possible selection:

Example 4 How many ways to select a 3 -person committee from a group of 10 persons?

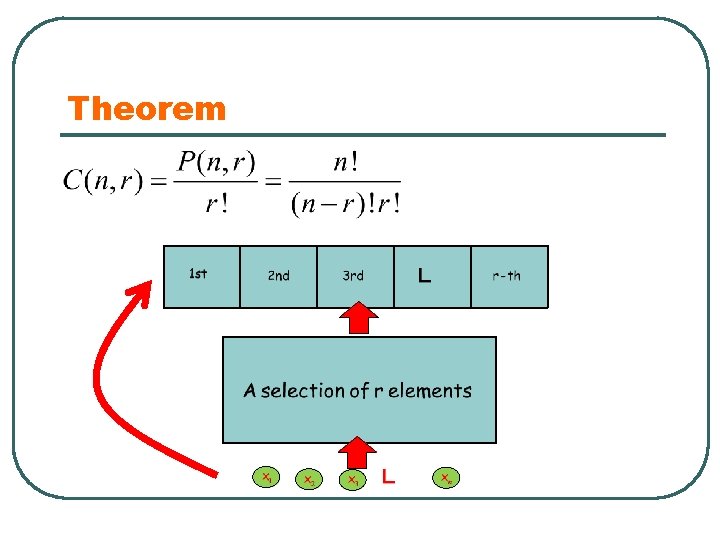
Theorem

Theorem

Example 5 How many ways to select a committee of 2 women and 3 men from a group of 5 women and 6 men?

Example 6(a) Given a standard deck of 52 playing cards. How many 5 -card hands are possible?

Example 6(b) Given a standard deck of 52 playing cards. How many 5 -card hands with the same suit are possible?