MAT 2720 Discrete Mathematics Section 6 1 Basic

MAT 2720 Discrete Mathematics Section 6. 1 Basic Counting Principles http: //myhome. spu. edu/lauw

Bonus Points Events

Bonus Points Events l l l Very Meaningful Career. Very well Compensated. Up to 2 bonus points for attending each meeting* Light refreshment. Limited seats.

General Goals l l Develop counting techniques. Set up a framework for solving counting problems. The key is not (just) the correct answers. The key is to explain to your audiences how to get to the correct answers.

Goals l Basics of Counting • Addition Principle • Multiplication Principle • Inclusion-Exclusion Principle

Addition Principle

Example 3 Pick a person to joint a university committee. # of possible ways = ?

Analysis Pick a person to joint a university committee. # of possible ways = ? The 2 sets:

Addition Principle l Number of possible element that can be selected from X 1 or X 2 or …or Xk is l OR

Multiplication Principle

Example 1 License Plate LLL-DDD # of possible plates = ?

Analysis License Plate LLL-DDD # of possible plates = ? Procedure: Step 1: Step 2: Step 3: Step 4: Step 5: Step 6:

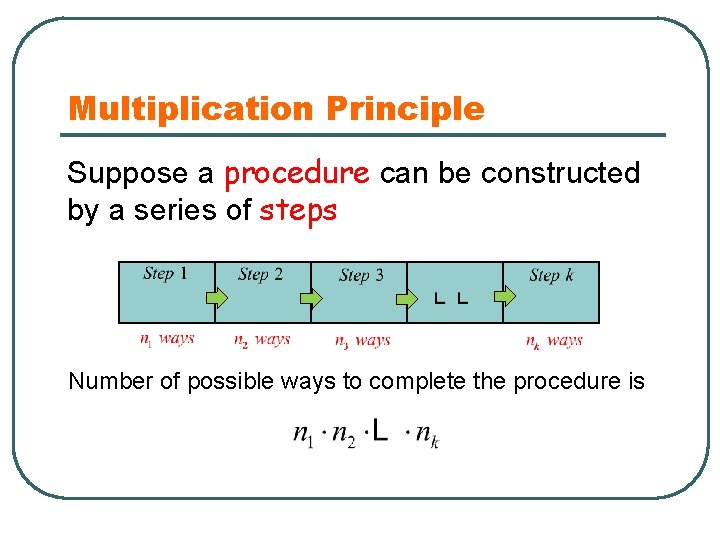
Multiplication Principle Suppose a procedure can be constructed by a series of steps Number of possible ways to complete the procedure is

Example 2(a) Form a string of length 4 from the letters A, B, C , D, E without repetitions. How many possible strings?

Example 2(b) Form a string of length 4 from the letters A, B, C , D, E without repetitions. How many possible strings begin with B?

Example 4 A 6 -person committee composed of A, B, C , D, E, and F is to select a chairperson, secretary, and treasurer.

Example 4 (a) In how many ways can this be done?

Example 4 (b) In how many ways can this be done if either A or B must be chairperson?

Example 4 (c) In how many ways can this be done if E must hold one of the offices?

Example 4 (d) In how many ways can this be done if both A and D must hold office?

Example 4 (e) We need the Inclusion-Exclusion Principle for this part.

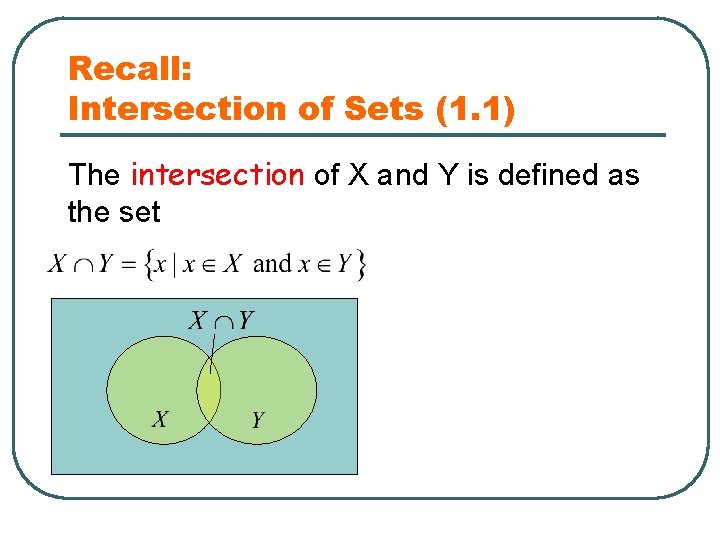
Recall: Intersection of Sets (1. 1) The intersection of X and Y is defined as the set

Recall: Intersection of Sets (1. 1) The intersection of X and Y is defined as the set

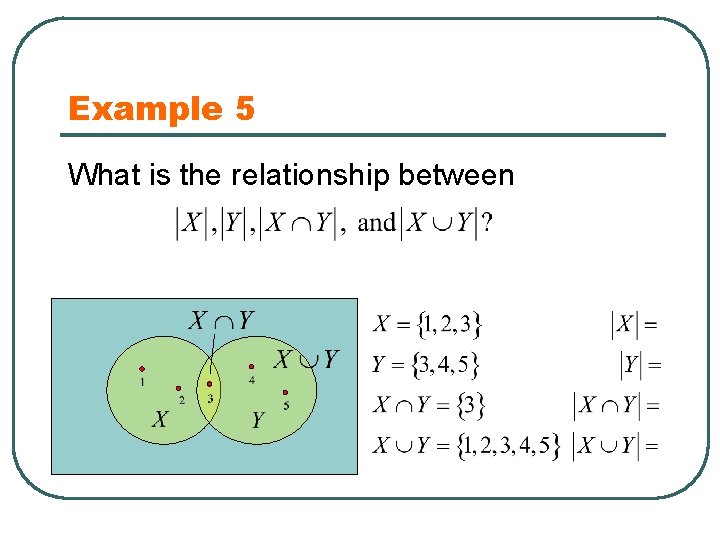
Example 5 What is the relationship between

Inclusion-Exclusion Principle

Example 4(e) How many selections are there in which either A or D or both are officers? .

Expectations l Some explanations in words are required. In particular, when using the Multiplication Principle, use the “steps” to explain your calculations l A conceptual diagram may be helpful.