MAT 2401 Linear Algebra 4 2 Vector Spaces

MAT 2401 Linear Algebra 4. 2 Vector Spaces http: //myhome. spu. edu/lauw

HW l Written Homework

Recall l We have seen examples of “space” (collection of mathematical objects) that have the 10 properties. • Rn, n-space (n Dimensional Real Vector Space) • P 2, Polynomials of degree at most 2. l Of course, there also examples of spaces that do not have all the 10 properties.

Generalization and Abstraction l l l We would like to generalize the idea of “vectors”. We are interested to those “spaces” that obey these 10 “axioms”. In mathematics, an axiom is a rule. These basic assumptions about a system allow theorems to be developed.

Vector Spaces

Ingredients of Vector Spaces Collection of “Vectors” Scalars Vector Addition Scalar Multiplication

Example 1 R 2 Collection of “Vectors” Scalars Vector Addition Scalar Multiplication

Example 2 Rn Collection of “Vectors” Scalars Vector Addition Scalar Multiplication

Example 3 M 2, 2 Collection of “Vectors” Scalars Vector Addition Scalar Multiplication

Example 4 P 2 Collection of “Vectors” Scalars Vector Addition Scalar Multiplication

Example 5 C(- , ) Collection of “Vectors” Scalars Vector Addition Scalar Multiplication

Summary of Important Vector Spaces

Properties of Scalar Multiplication

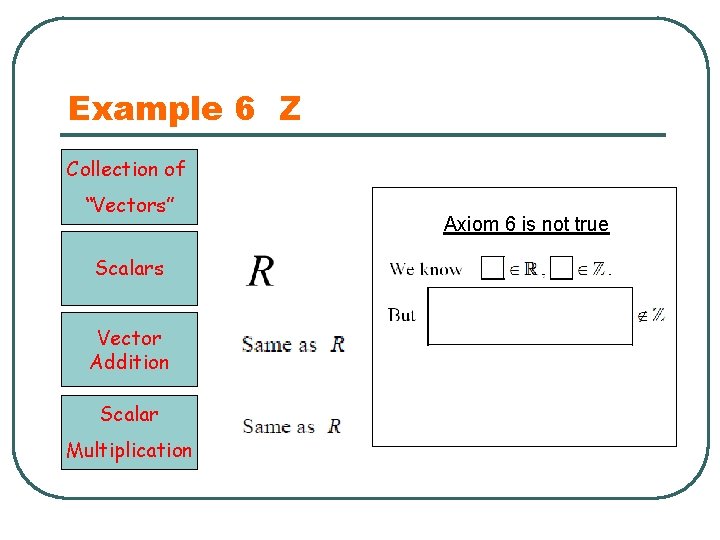
Example 6 Z Collection of “Vectors” Scalars Vector Addition Scalar Multiplication Axiom 6 is not true

Vector Spaces

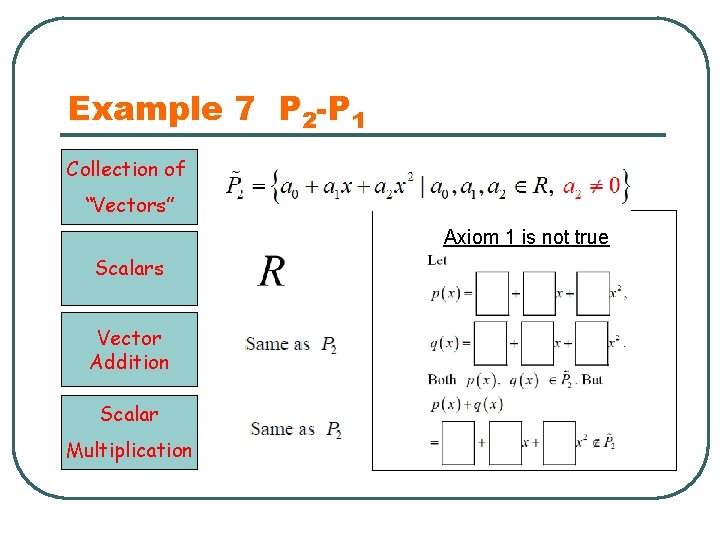
Example 7 P 2 -P 1 Collection of “Vectors” Axiom 1 is not true Scalars Vector Addition Scalar Multiplication

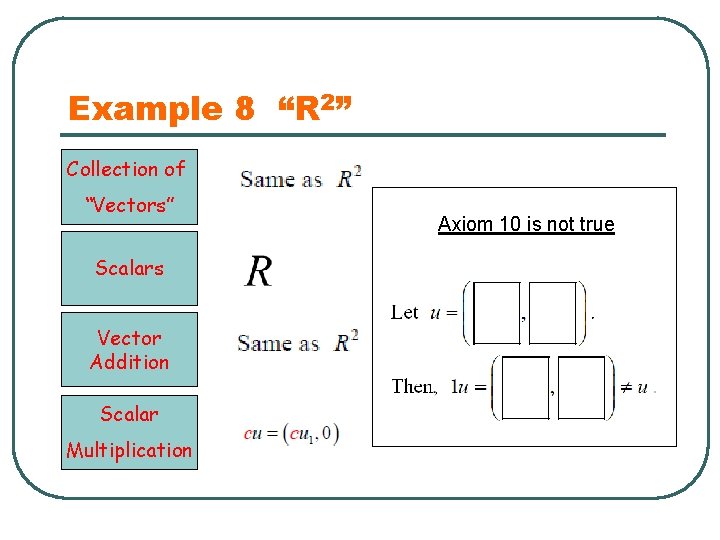
Example 8 “R 2” Collection of “Vectors” Scalars Vector Addition Scalar Multiplication Axiom 10 is not true

Method to Disprove an Axiom 1. Axiom x is not true. 2. Give an example to illustrate that Axiom x is not true. (This type of method is called Counter Examples. )