MAT 2401 Linear Algebra 3 1 The Determinant

MAT 2401 Linear Algebra 3. 1 The Determinant of a Matrix http: //myhome. spu. edu/lauw

HW l Written Homework

Preview l l How do I know a matrix is invertible? We will look at determinant that tells us the answer.

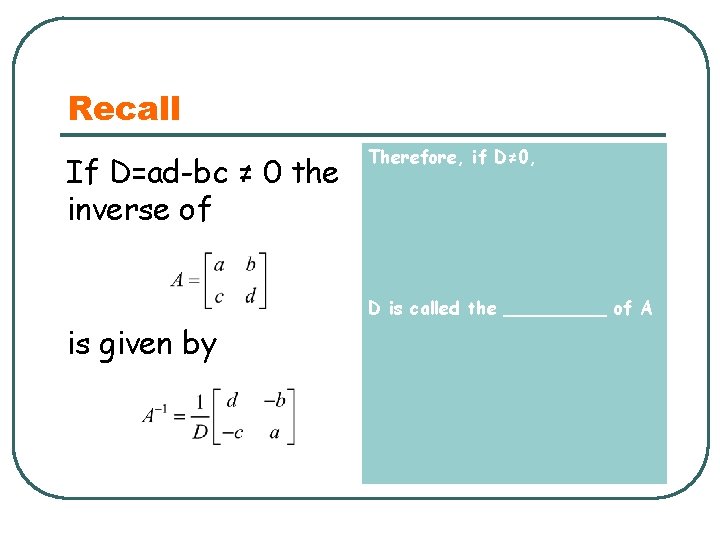
Recall If D=ad-bc ≠ 0 the inverse of Therefore, if D≠ 0, D is called the _____ of A is given by

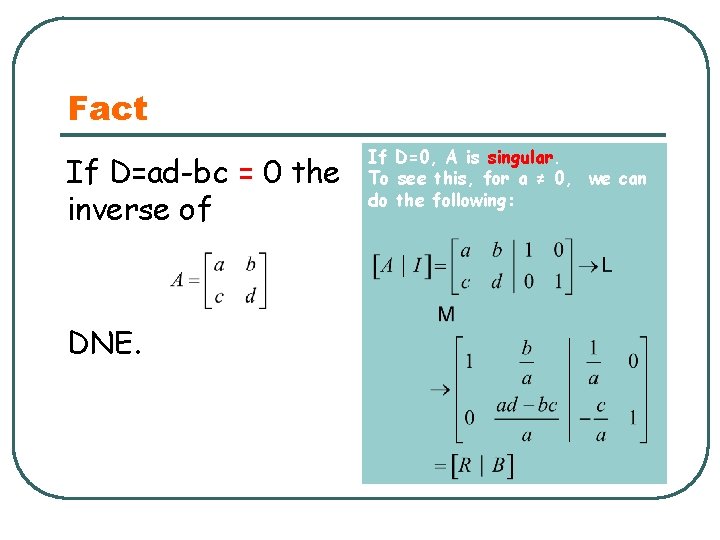
Fact If D=ad-bc = 0 the inverse of DNE. If D=0, A is singular. To see this, for a ≠ 0, we can do the following:

The Task Given a square matrix A, we wish to associate with A a scalar det(A) that will tell us whether or not A is invertible

Fact (3. 3) l A square matrix A is invertible if and only if det(A)≠ 0

Interesting Comments Interesting comments from a text: l The concept of determinant is subtle and not intuitive, and researchers had to accumulate a large body of experience before they were able to formulate a “correct” definition for this number.

n=2 1. Notations: 2. Mental picture for memorizing

n=3

n=3 Q 1: What? Do I need to remember this? Q 2: What if A is 4 x 4 or bigger? Q 3: Is there a formula for 1 x 1 matrix?

Observations

Observations We need: 1. a notion of “one size smaller” but related determinants. 2. a way to assign the correct signs to these smaller determinants. 3. a way to extend the computations to nxn matrices.

Minors and Cofactors A=[aij], a nxn Matrix. Let Mij be the determinant of the (n-1)x(n-1) matrix obtained from A by deleting the row and column containing aij. Mij is called the minor of aij. Example:

Minors and Cofactors A=[aij], a nxn Matrix. Let Cij =(-1)i+j Mij Cij is called the cofactor of aij. Example:

n=3

Determinants l l Formally defined Inductively by using cofactors (minors) for all nxn matrices in a similar fashion. The process is sometimes referred as Cofactors Expansion.

Cofactors Expansion (across the first column) The determinant of a nxn matrix A=[aij] is a scalar defined by

Example 1

Remark The cofactor expansion can be done across any column or any row.

Cofactors Expansion

Special Matrices and Their Determinants l l (Square) Zero Matrix det(O)=? Identity Matrix det(I)=? We will come back to this later….

Upper Triangular Matrix

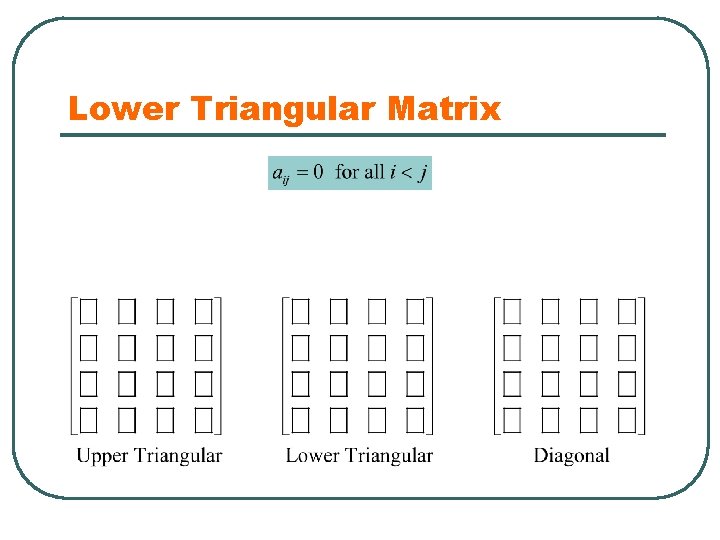
Lower Triangular Matrix

Diagonal Matrix

Diagonal Matrix Q: T or F: A diagonal matrix is upper triangular?

Example 2

Determinant of a Triangular Matrix Let A=[aij], be a nxn Triangular Matrix, det(A)=

Special Matrices and Their Determinants l l (Square) Zero Matrix det(O)= Identity Matrix det(I)=