Mastery Mathematics Programmes of Study 2014 National Curriculum

Mastery Mathematics Programmes of Study 2014 National Curriculum

Could do better: Using international comparisons to refine the National Curriculum in England Foreword by the Secretary of State for Education This fascinating and insightful paper offers a concise analysis of some of the problems with our current National Curriculum and helps explain why so many other nations are outpacing us in educational performance. The debate about our National Curriculum now has to be seen in an international context. The best-performing education nations deliberately set out to compare themselves against international benchmarks – learning from each other and constantly asking what is required to help all children do better. Hong Kong and Singapore have sought to maintain their pre-eminence by reviewing their national curricula while Australia and US states are also looking to see how they can modernise their curriculum offers. While other countries have developed coherent national curricula that allow for the steady accumulation of knowledge and conceptual understanding, our National Curriculum has, sadly, lost much of its initial focus. As Tim Oates explains, “in all high-performing systems, the fundamentals of subjects are strongly emphasised, have substantial time allocation, and are the focus of considerable attention in learning programmes” – yet in England we have been moving away from this goal. In recent years, there has been a loss of stability and purpose with new subjects and topics added – more often in response to pressure groups than for sound pedagogical reasons. The most recent overhaul of the National Curriculum in 2007 was a serious backward step as concepts were replaced with vague generic statements of little value. Previous reviews of the curriculum sought to over-specify classroom practice. As Tim Oates says, the decision to teach in a particular way may not be appropriate for all schools or teachers, but what is crucial is first identifying the crucial concepts and ideas that each year group should learn. Shortly, my Department will launch its own review of the National Curriculum and the remit will explicitly, for the first time, require benchmarking against the most successful school systems. This – as Tim makes clear – has to be done with great care to avoid learning the wrong lessons from countries with very different cultures. But it is essential if we are to keep pace with the world’s best. This paper is the perfect introduction to the challenge we face. Hong Kong and Singapore have sought to maintain their preeminence by reviewing their national curricula while Australia and US states are also looking to see how they can modernise their curriculum offers. Shortly, my Department will launch its own review of the National Curriculum and the remit will explicitly, for the first time, require benchmarking against the most successful school systems. This – as Tim makes clear – has to be done with great care to avoid learning the wrong lessons from countries with very different cultures. But it is essential if we are to keep pace with the world’s best. Rt Hon Michael Gove MP

Mastery approaches to mathematics ‘Mastery’ in high performing countries O The content and principles underpinning the 2014 mathematics curriculum reflect those found in high performing education systems internationally, particularly those of east and south-east Asian countries such as Singapore, Japan, South Korea and China. The OECD suggests that by age 15 students from these countries are on average up to three years ahead in maths compared to 15 year olds in England. What underpins this success is the far higher proportion of pupils reaching a high standard and the relatively small gaps in attainment between pupils in comparison to England. O Though there are many differences between the education systems of England those of east and south-east Asia, we can learn from the ‘mastery’ approach to teaching commonly followed in these countries.

Key Features of the mastery approach O Curriculum design O Teaching resources O Lesson design O Teaching methods O Pupil support and differentiation O Productivity and practice

Key Features of the mastery approach O Curriculum design A detailed, structured curriculum is mapped out across all phases, ensuring continuity and supporting transition. Effective mastery curricula in mathematics are designed in relatively small carefully sequenced steps, which must each be mastered before pupils move to the next stage. Fundamental skills and knowledge are secured first. This often entails focusing on curriculum content in considerable depth at early stages.

Key Features of the mastery approach O Teaching resources A coherent programme of high quality curriculum materials is used to support classroom teaching. Concrete and pictorial representations of mathematics are chosen carefully to help build procedural and conceptual knowledge together. Exercises are structured with great care to build deep conceptual knowledge alongside developing procedural fluency. The focus is on the development of deep structural knowledge and the ability to make connections. Making connections in mathematics deepens knowledge of concepts and procedures, ensures what is learnt is sustained over time, and cuts down the time required to assimilate and master later concepts and techniques.

Key Features of the mastery approach O Lesson design Lessons are crafted with similar care and are often perfected over time with input from other teachers, drawing on evidence from observations of pupils in class. Lesson designs set out in detail well-tested methods to teach a given mathematical topic. They include a variety of representations needed to introduce and explore a concept effectively and also set out related teacher explanations and questions to pupils.

Key Features of the mastery approach O Teaching methods In highly successful systems, teachers are clear that their role is to teach in a precise way which makes it possible for all pupils to engage successfully with tasks at the expected level of challenge. Pupils work on the same tasks and engage in common discussions. Concepts are often explored together to make mathematical relationships explicit and strengthen pupils’ understanding of mathematical connectivity. Precise questioning during lessons ensures that pupils develop fluent technical proficiency and think deeply about the underpinning mathematical concepts. There is no prioritisation between technical proficiency and conceptual understanding; in successful classrooms these two key aspects of mathematical learning are developed in parallel.

Key Features of the mastery approach O Pupil support and differentiation Taking a mastery approach, differentiation occurs in the support and intervention provided to different pupils, not in the topics taught, particularly at earlier stages. There is no differentiation in content taught, but the questioning and scaffolding individual pupils receive in class as they work through problems will differ, with higher attainers challenged through more demanding problems which deepen their knowledge of the same content. Pupils’ difficulties and misconceptions are identified through immediate formative assessment and addressed with rapid intervention – commonly through individual or small group support later the same day: there are very few “closing the gap” strategies, because there are very few gaps to close.

Key Features of the mastery approach O Productivity and practice Fluency comes from deep knowledge and practice. Pupils work hard and are productive. At early stages, explicit learning of multiplication tables is important in the journey towards fluency and contributes to quick and efficient mental calculation. Practice leads to other number facts becoming second nature. The ability to recall facts from long term memory and manipulate them to work out other facts is also important. All tasks are chosen and sequenced carefully, offering appropriate variation in order to reveal the underlying mathematical structure to pupils. Both class work and homework provide this ‘intelligent practice’, which helps to develop deep and sustainable knowledge.

2014 Maths Curriculum O The new mathematics curriculum goes further than the previous curriculum O There is renewed emphasis on problemsolving O The programme of study is set out on a year-by-year basis

Mathematics programmes of study key stage 1 and 2 Aims The national curriculum for mathematics aims to ensure that all pupils: O become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately. O reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language O can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.

Mathematics programmes of study key stage 1 and 2 Spoken language O The national curriculum for mathematics reflects the importance of spoken language in pupils’ development across the whole curriculum – cognitively, socially and linguistically. The quality and variety of language that pupils hear and speak are key factors in developing their mathematical vocabulary and presenting a mathematical justification, argument or proof. They must be assisted in making their thinking clear to themselves as well as others and teachers should ensure that pupils build secure foundations by using discussion to probe and remedy their misconceptions.

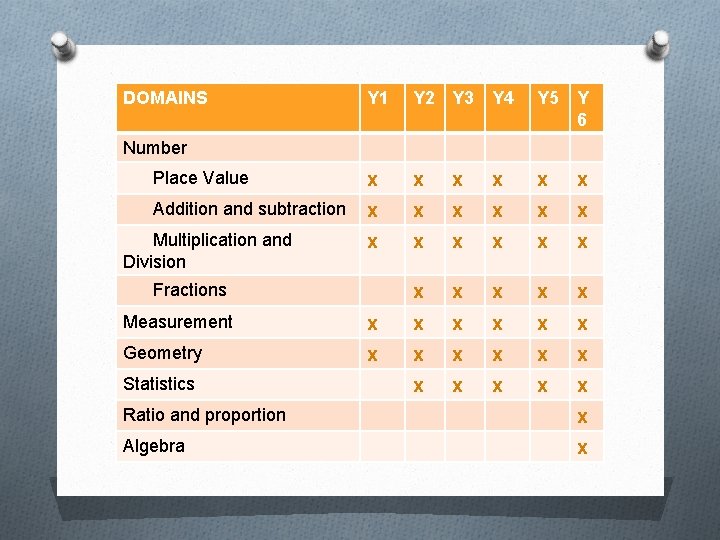
Organisation of objectives O Objectives set by year group O Organised into domains

DOMAINS Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Place Value x x x Addition and subtraction x x x x x Number Multiplication and Division Fractions Measurement x x x Geometry x x x Statistics Ratio and proportion x Algebra x

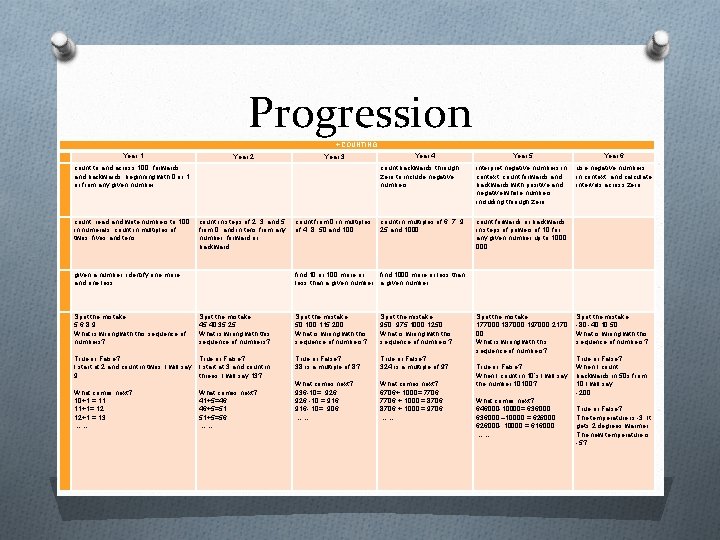
Progression +COUNTING Year 1 Year 2 Year 3 count to and across 100, forwards and backwards, beginning with 0 or 1, or from any given number count, read and write numbers to 100 in numerals; count in multiples of twos, fives and tens count in steps of 2, 3, and 5 from 0, and in tens from any number, forward or backward given a number, identify one more and one less count from 0 in multiples of 4, 8, 50 and 100; Year 5 Year 6 count backwards through zero to include negative numbers Year 4 interpret negative numbers in context, count forwards and backwards with positive and negative whole numbers, including through zero use negative numbers in context, and calculate intervals across zero count in multiples of 6, 7, 9, 25 and 1000 count forwards or backwards in steps of powers of 10 for any given number up to 1000 find 10 or 100 more or find 1000 more or less than a given number Spot the mistake: 5, 6, 8, 9 What is wrong with this sequence of numbers? Spot the mistake: 45, 40, 35, 25 What is wrong with this sequence of numbers? Spot the mistake: 50, 100, 115, 200 What is wrong with this sequence of numbers? Spot the mistake: 950, 975, 1000, 1250 What is wrong with this sequence of numbers? True or False? I start at 2 and count in twos. I will say 9 True or False? I start at 3 and count in threes. I will say 13? True or False? 38 is a multiple of 8? True or False? 324 is a multiple of 9? What comes next? 10+1 = 11 11+1= 12 12+1 = 13 ……. . What comes next? 41+5=46 46+5=51 51+5=56 …… What comes next? 936 -10= 926 -10 = 916 - 10= 906 ……. What comes next? 6706+ 1000= 7706 + 1000 = 8706 + 1000 = 9706 …… Spot the mistake: 177000, 187000, 197000, 2170 00 What is wrong with this sequence of numbers? True or False? When I count in 10’s I will say the number 10100? What comes next? 646000 -10000= 636000 – 10000 = 626000 - 10000 = 616000 ……. Spot the mistake: -80, -40, 10, 50 What is wrong with this sequence of numbers? True or False? When I count backwards in 50 s from 10 I will say -200 True or False? The temperature is -3. It gets 2 degrees warmer. The new temperature is -5?

Pupils who grasp concepts rapidly should be challenged through rich and sophisticated problems before any acceleration through new content. Those pupils who are not sufficiently fluent with earlier material should consolidate their understanding, including through additional practice, before moving on. O NRICH – curriculum mapping doc.

Attainment targets By the end of each key stage, pupils are expected to know, apply and understand the matters, skills and processes specified in the relevant programme of study.

MASTERY MATHS

Classroom visits O We invite you now to go and spend 30 mins (9: 00 – 9: 30 am) in your child’s class. O Please feel free to sit by your child and get involved in the investigation.