Master de Physique M 2 Processus dynamiques dinteraction

Master de Physique M 2 Processus dynamiques d’interaction entre atomes, molécules, surfaces et photons 20 hrs Objectifs: Acquérir les bases pour réaliser un travail de recherche dans la modélisation des phénomènes quantiques apparaissant dans: ● les interactions laser-matière ● les interactions gaz—surface ● les processus d’échange de charge ● la réactivité Déroulement: 4 cours de 5 h sur la base de chaque type d’interaction

Master de Physique M 2 Processus dynamiques d’interaction entre atomes, molécules, surfaces et photons 1. Cours 1 -4 Dynamique quantique des systèmes réactifs en phase gazeuse (B. Lepetit, Bât. 3 R 1 -108) 3. Cours 9 -11 Dynamique quantique des interactions gaz-surface (D. Lemoine, Bât. 3 R 1 -100) 2. Cours 4 -8 Dynamique quantique des systèmes en interaction avec des impulsions laser (C. Meier, Bât. 3 R 1 -103) 4. Cours 12 -14 Dynamique mixte quantique-classique: vers les systèmes à grand nombre de degrés de liberté (N. Halberstadt, Bât. 3 R 1 -216)

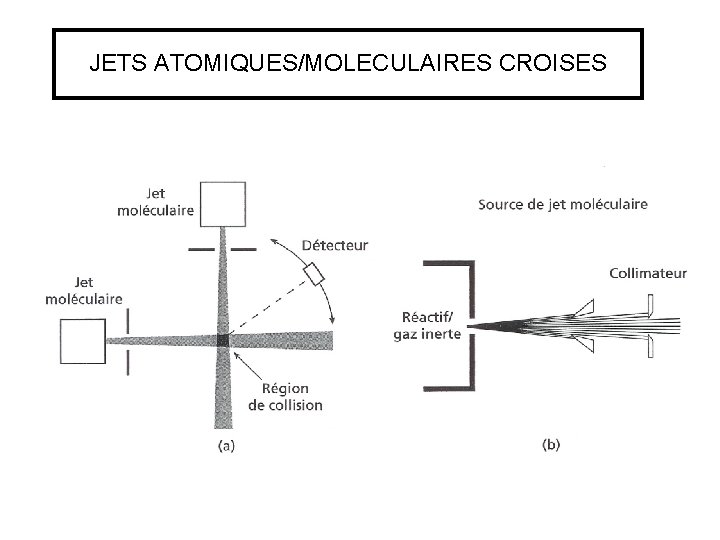
JETS ATOMIQUES/MOLECULAIRES CROISES

Collision de nuages atomiques froids Ec/k. B = 250 K Figure extraite de Thomas et al. PRL 93, 173201 (2004) Y 20 ( ) Onde d

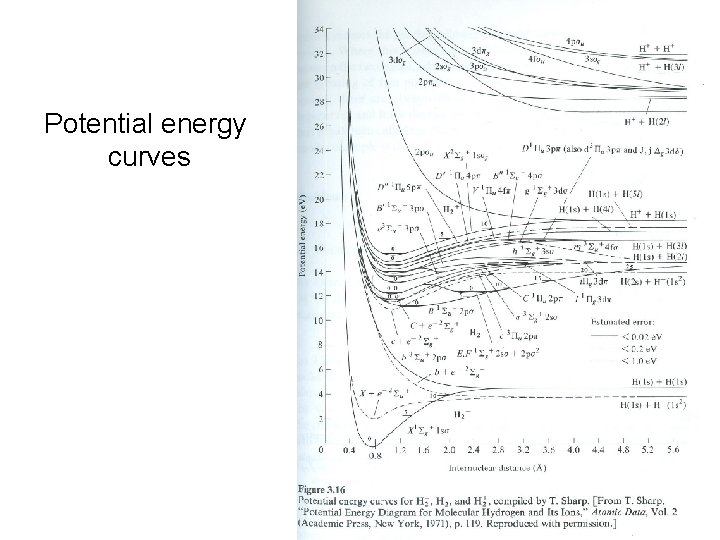
Potential energy curves

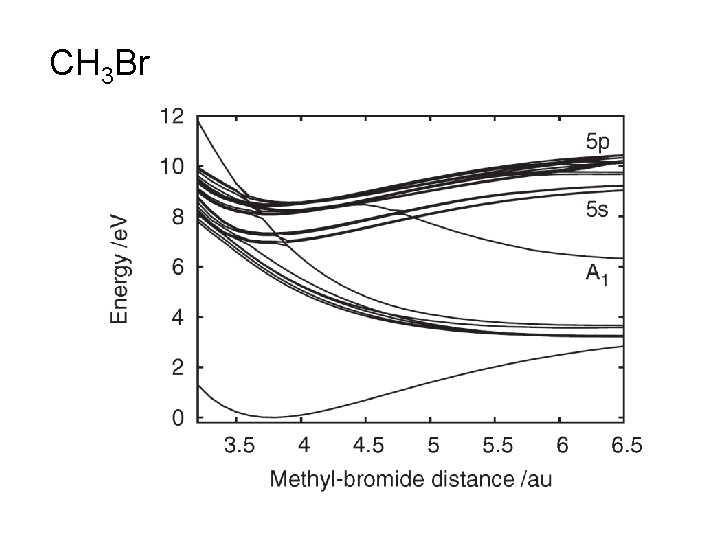
CH 3 Br

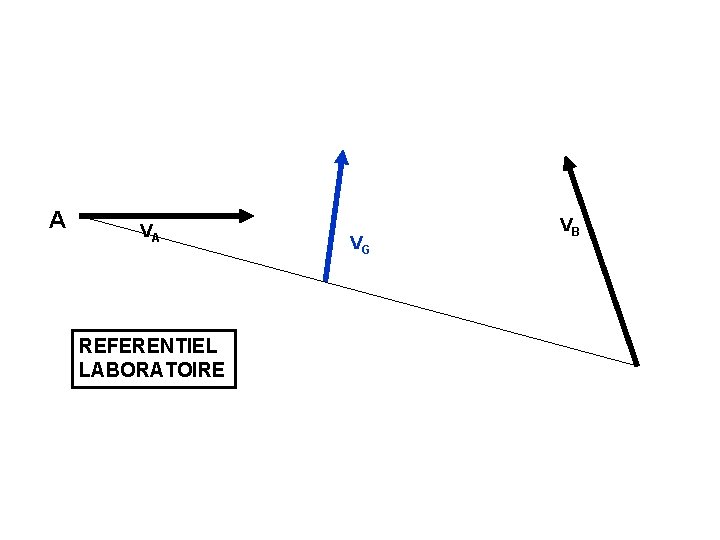
A VA REFERENTIEL LABORATOIRE VG VB

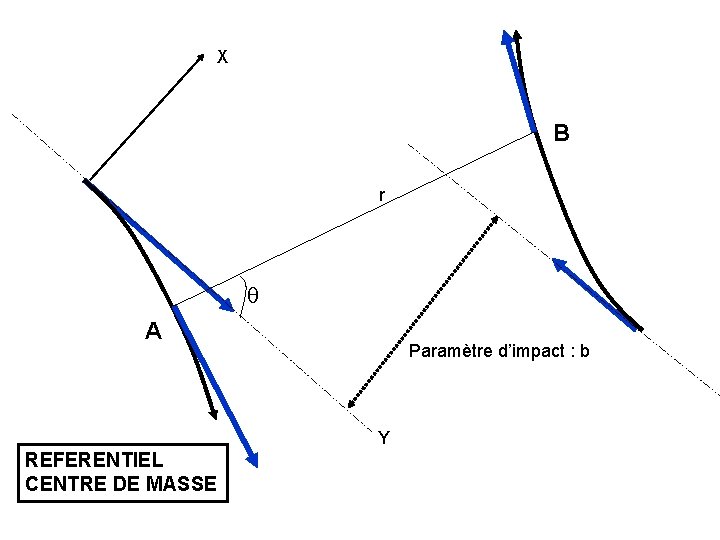
X B r A Paramètre d’impact : b Y REFERENTIEL CENTRE DE MASSE

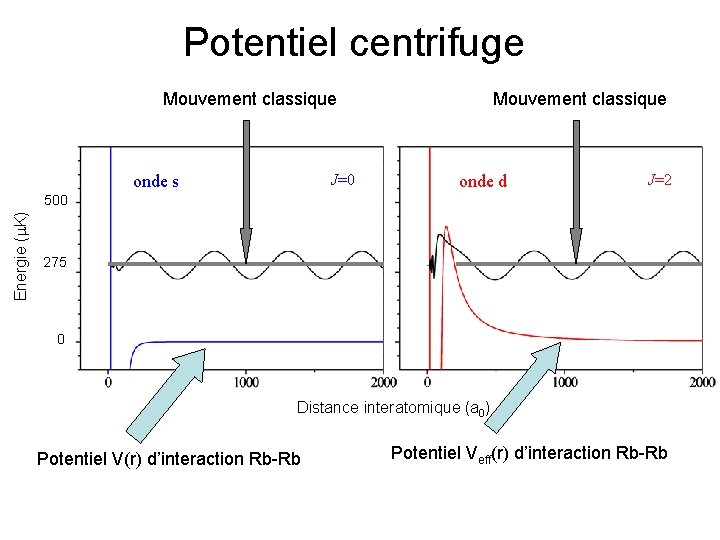
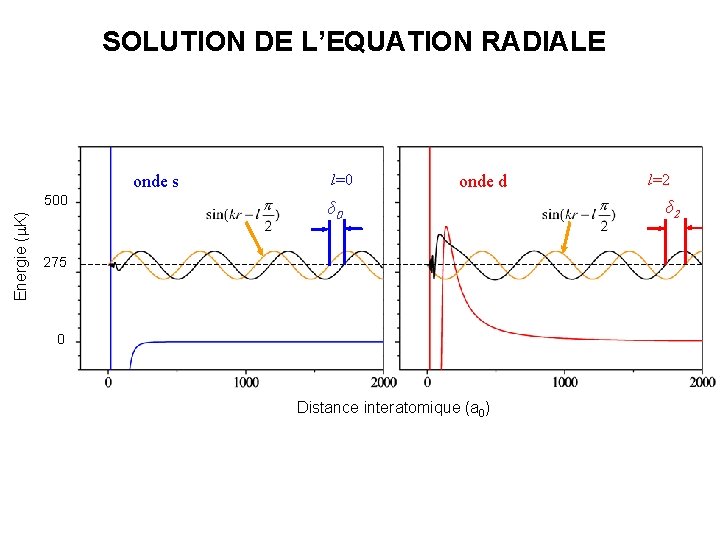
Potentiel centrifuge Mouvement classique J=0 onde s Mouvement classique onde d J=2 Energie ( K) 500 275 0 Distance interatomique (a 0) Potentiel V(r) d’interaction Rb-Rb Potentiel Veff(r) d’interaction Rb-Rb

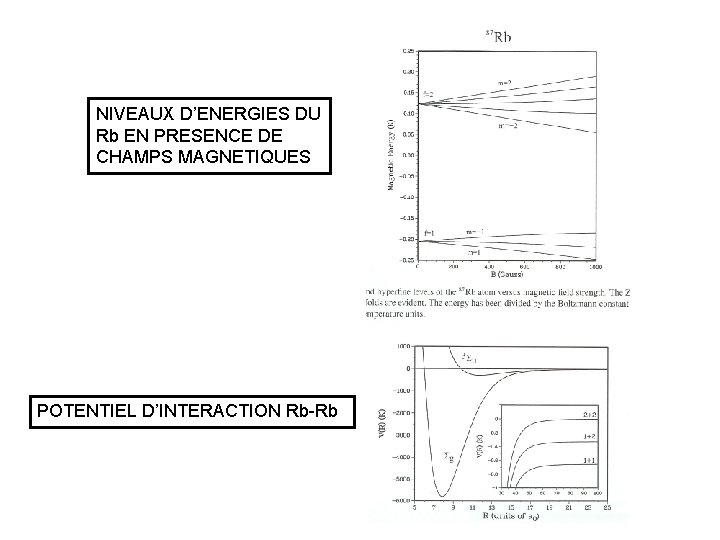
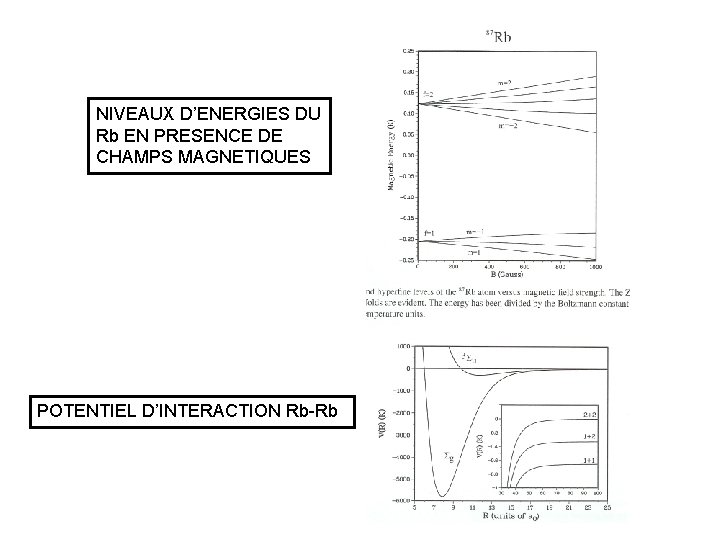
NIVEAUX D’ENERGIES DU Rb EN PRESENCE DE CHAMPS MAGNETIQUES POTENTIEL D’INTERACTION Rb-Rb

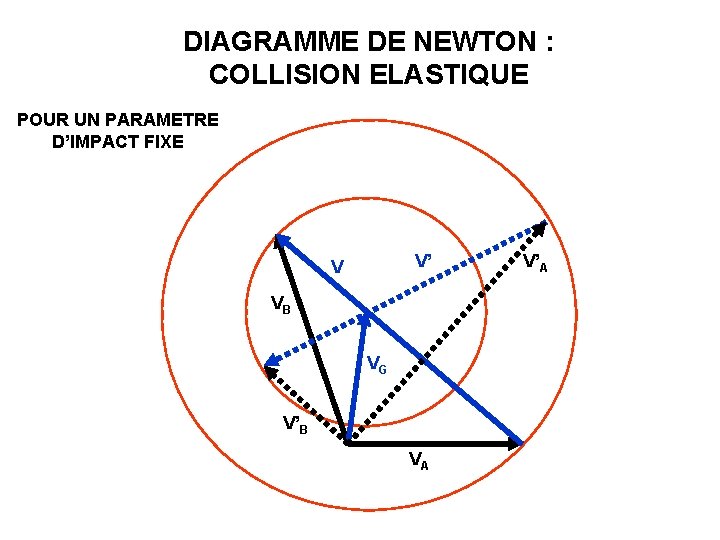
DIAGRAMME DE NEWTON : COLLISION ELASTIQUE POUR UN PARAMETRE D’IMPACT FIXE V’ V VB VG V’B VA V’A

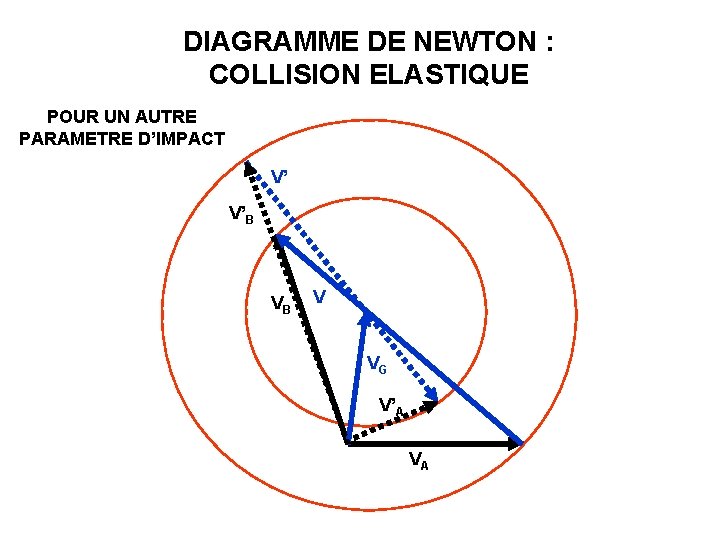
DIAGRAMME DE NEWTON : COLLISION ELASTIQUE POUR UN AUTRE PARAMETRE D’IMPACT V’ V’B VB V VG V’A VA

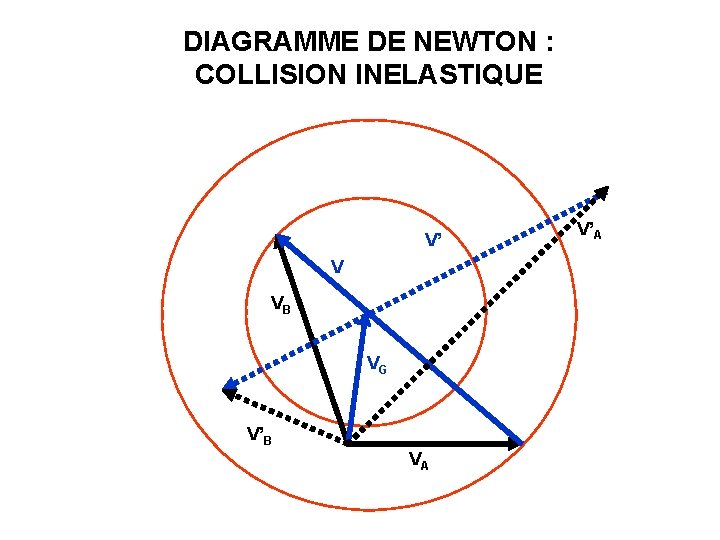
DIAGRAMME DE NEWTON : COLLISION INELASTIQUE V’ V VB VG V’B VA V’A

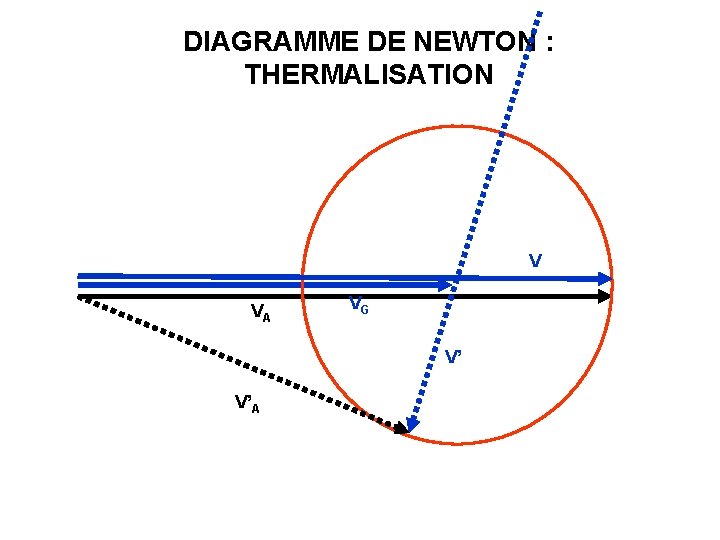
DIAGRAMME DE NEWTON : THERMALISATION V VA VG V’ V’A

SECTION EFFICACE

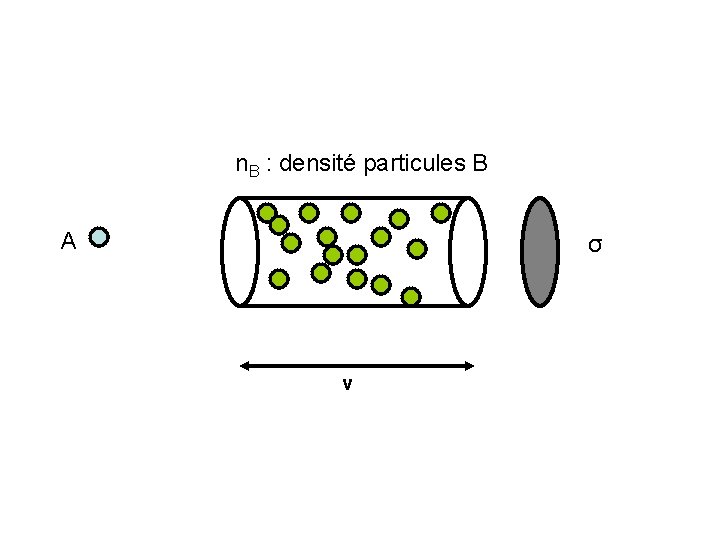
n. B : densité particules B A σ v

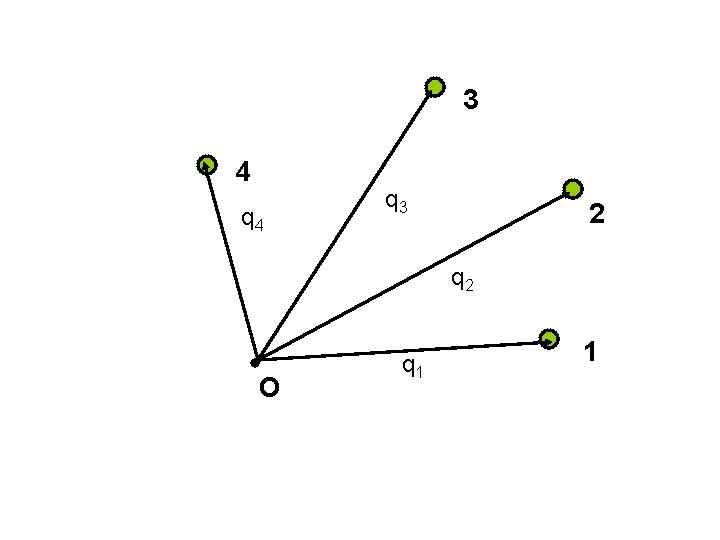
3 4 q 3 2 q 2 O q 1 1

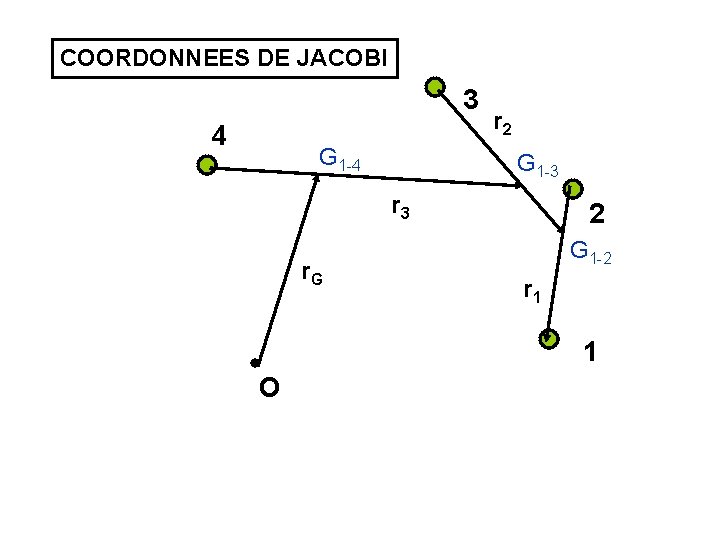
COORDONNEES DE JACOBI 3 4 G 1 -4 r 2 G 1 -3 r 3 r. G 2 G 1 -2 r 1 1 O

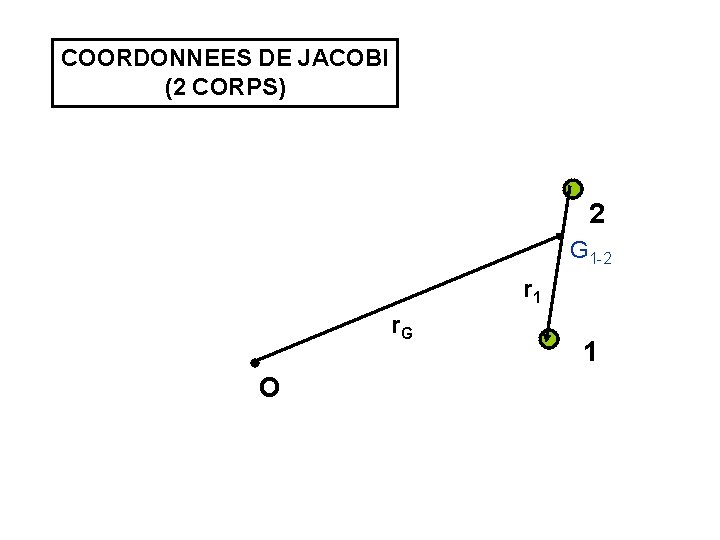
COORDONNEES DE JACOBI (2 CORPS) 2 G 1 -2 r 1 r. G O 1

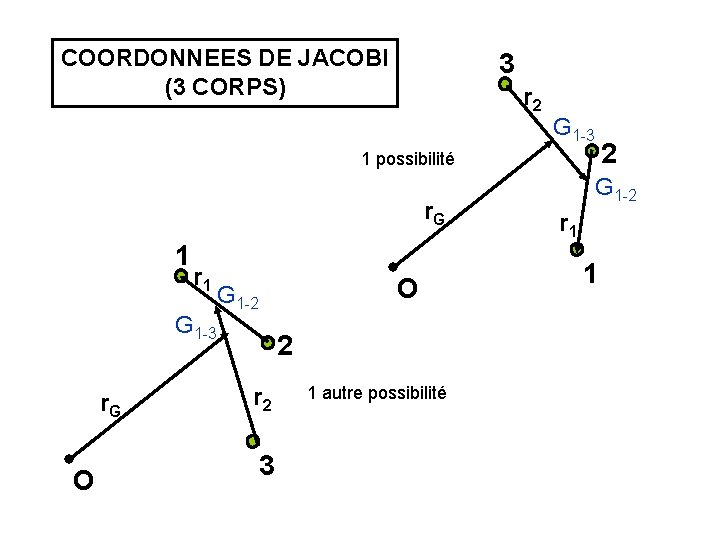
COORDONNEES DE JACOBI (3 CORPS) 3 r 2 G 1 -3 2 1 possibilité r. G 1 r 1 G 1 -3 r. G O O G 1 -2 2 r 2 3 1 autre possibilité G 1 -2 r 1 1

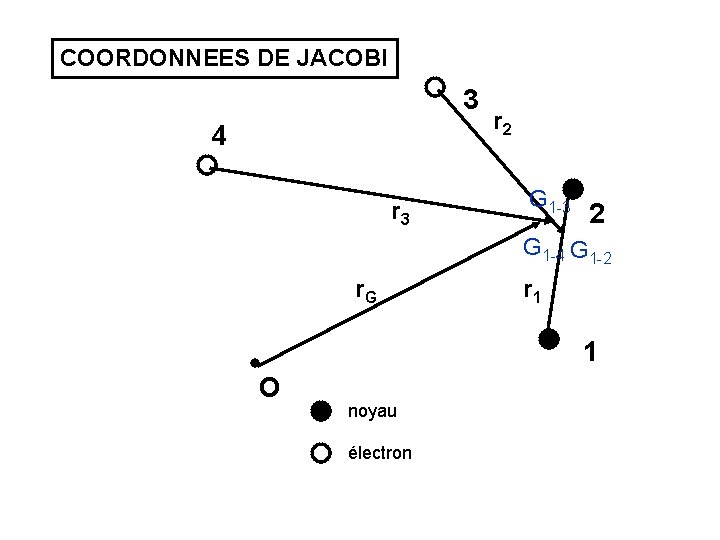
COORDONNEES DE JACOBI 3 4 r 3 r 2 G 1 -3 2 G 1 -4 G 1 -2 r. G r 1 1 O noyau électron

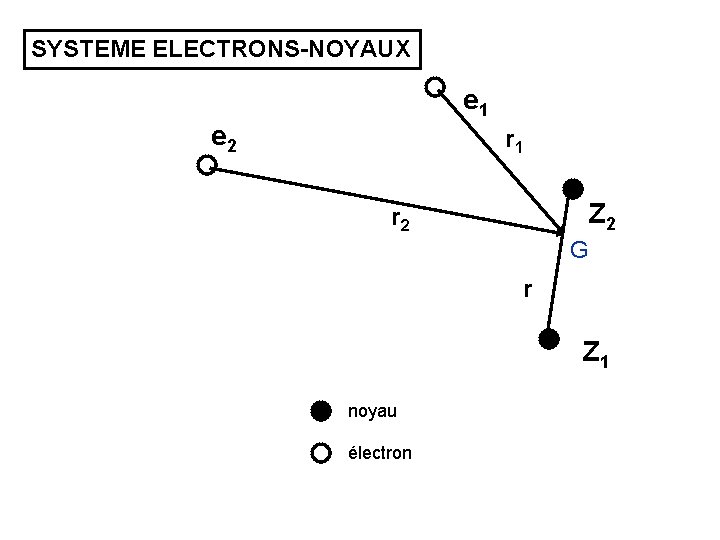
SYSTEME ELECTRONS-NOYAUX e 1 e 2 r 1 Z 2 r 2 G r Z 1 noyau électron

NIVEAUX D’ENERGIES DU Rb EN PRESENCE DE CHAMPS MAGNETIQUES POTENTIEL D’INTERACTION Rb-Rb

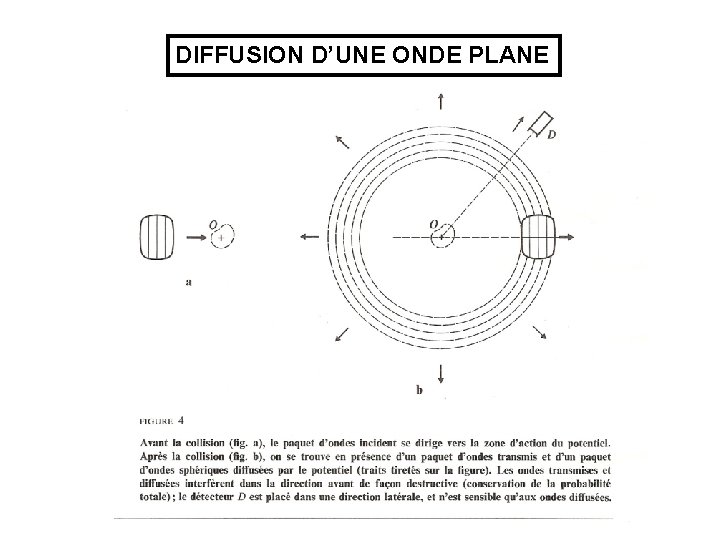
DIFFUSION D’UNE ONDE PLANE

SECTION EFFICACE

SOLUTION DE L’EQUATION RADIALE onde s Energie ( K) 500 l=0 onde d δ 0 275 0 Distance interatomique (a 0) l=2 δ 2

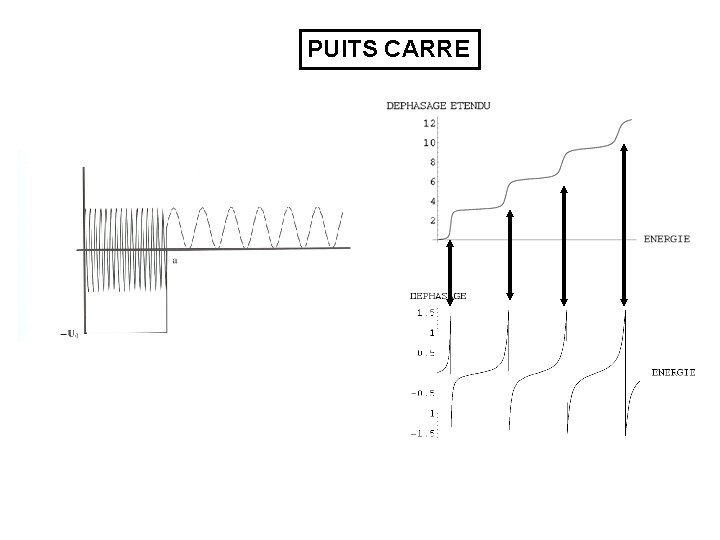
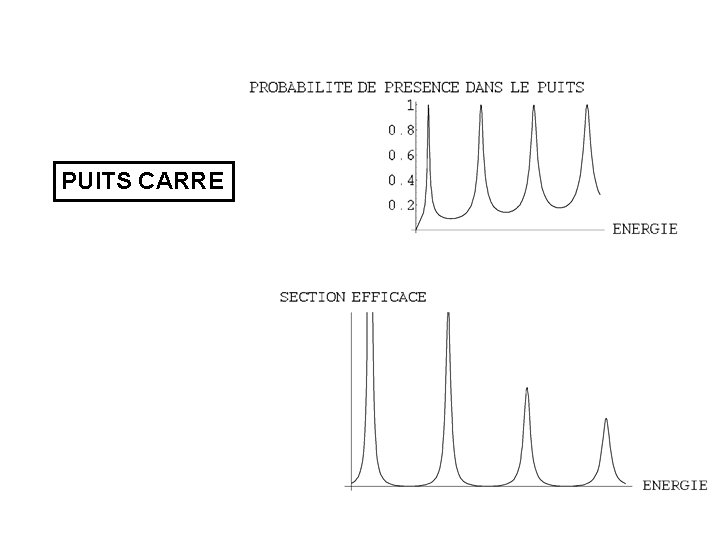
PUITS CARRE

PUITS CARRE

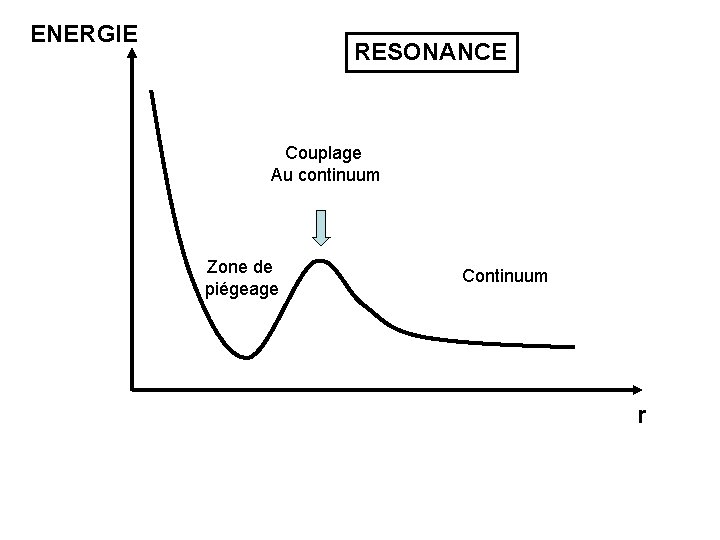
ENERGIE RESONANCE Couplage Au continuum Zone de piégeage Continuum r

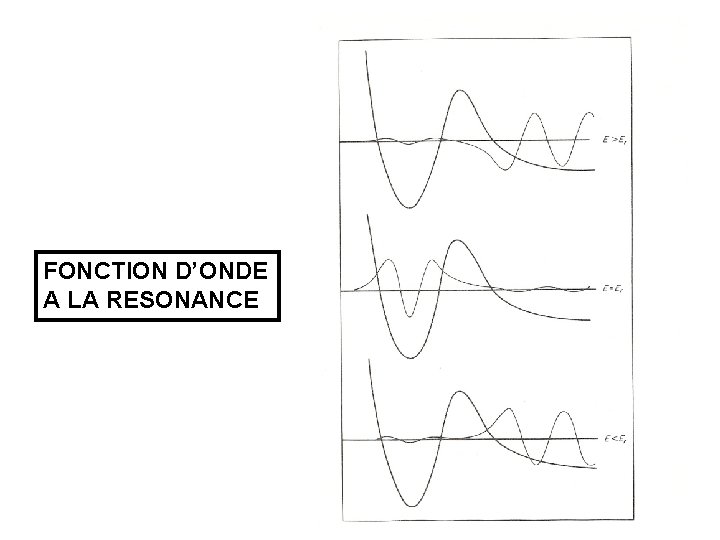
FONCTION D’ONDE A LA RESONANCE

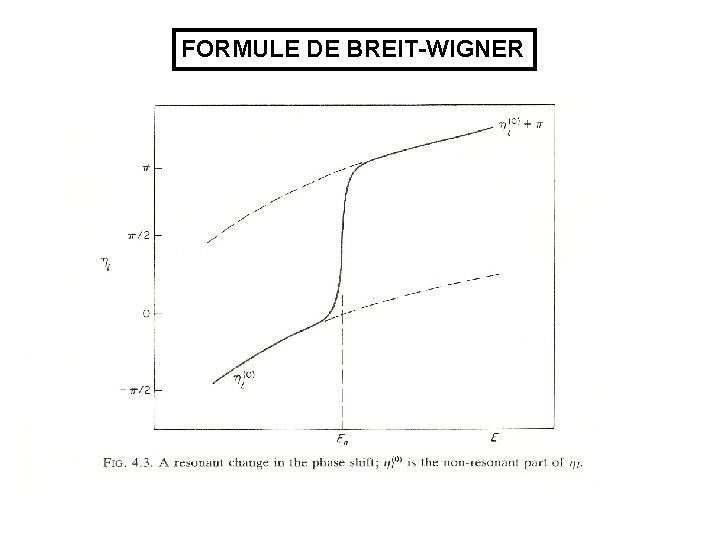
FORMULE DE BREIT-WIGNER

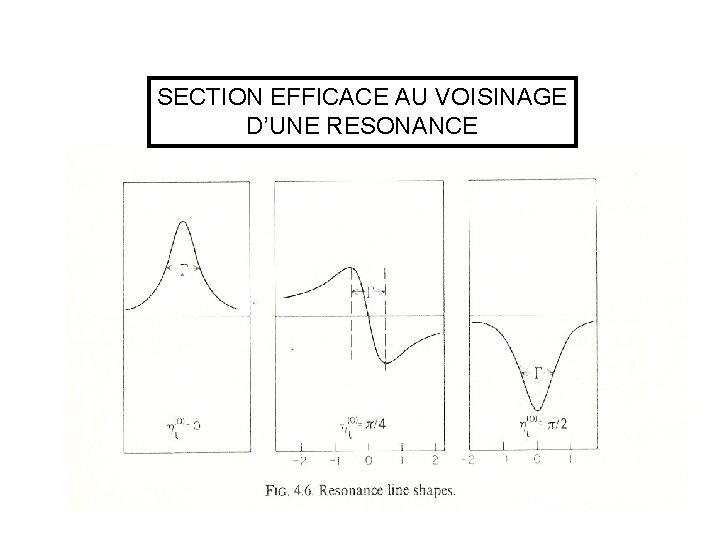
SECTION EFFICACE AU VOISINAGE D’UNE RESONANCE

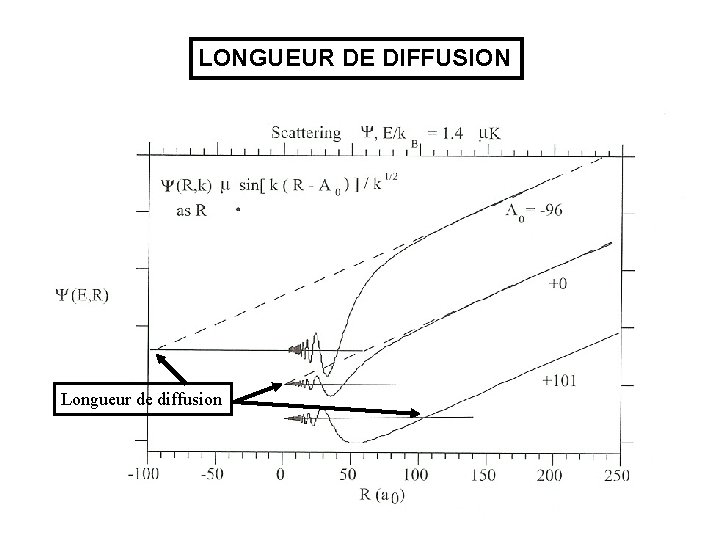
LONGUEUR DE DIFFUSION Longueur de diffusion

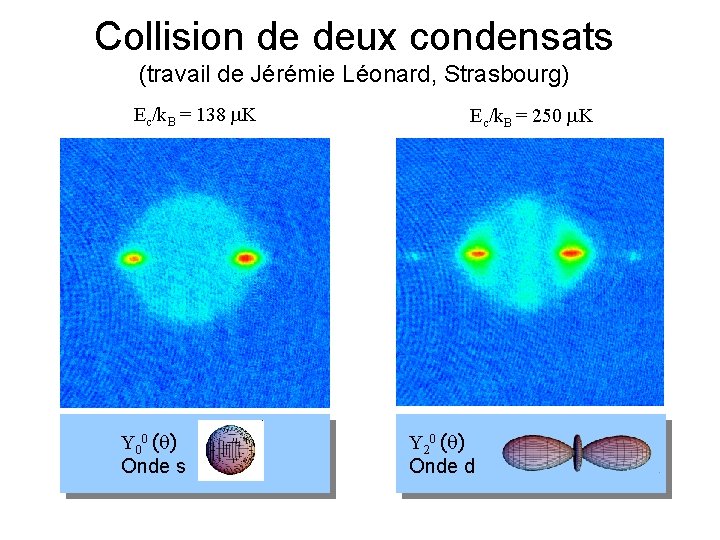
Collision de deux condensats (travail de Jérémie Léonard, Strasbourg) Ec/k. B = 138 K Y 00 ( ) Onde s Ec/k. B = 250 K Y 20 ( ) Onde d

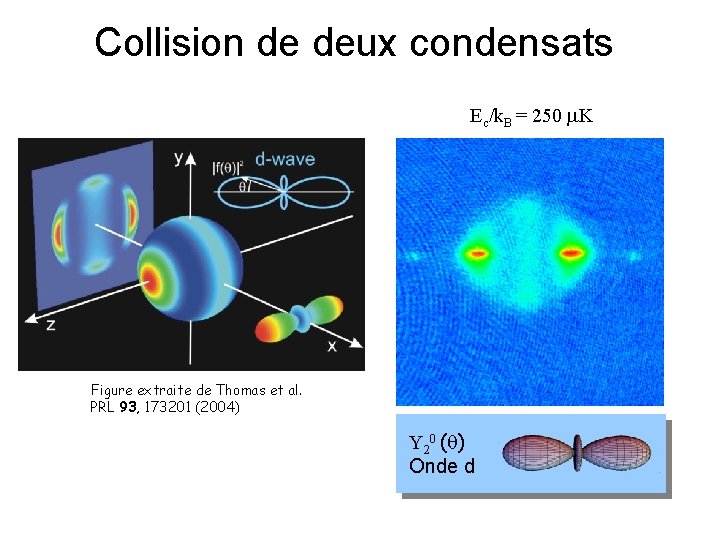
Collision de deux condensats Ec/k. B = 250 K Figure extraite de Thomas et al. PRL 93, 173201 (2004) Y 20 ( ) Onde d

Energie de collision = 138 K Expérience: σ( ) z cos( ) x z Densité optique Section efficace différentielle Tomographie (Bosons identiques => Symétrisation) Théorie : l : Déphasage de l’onde partielle j (faible énergie de collision) | Onde s + Onde d | 2 Þ Interférences

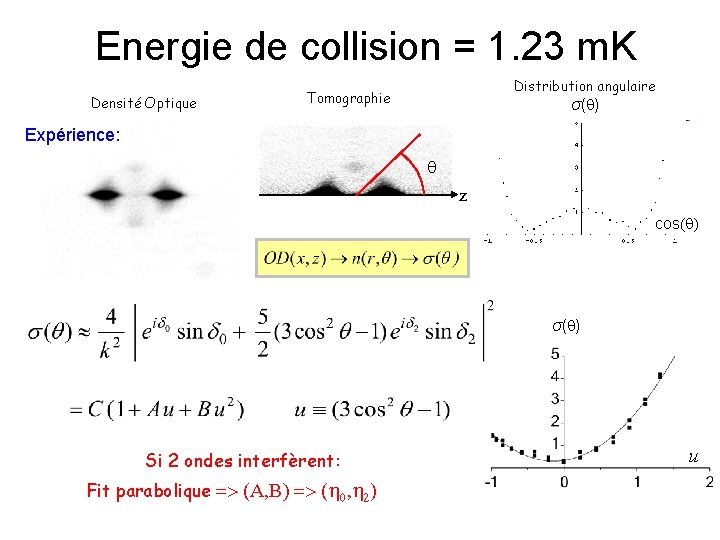
Energie de collision = 1. 23 m. K Densité Optique Distribution angulaire Tomographie σ( ) Expérience: z cos( ) σ( ) Si 2 ondes interfèrent: Fit parabolique => (A, B) => (h 0, h 2) u

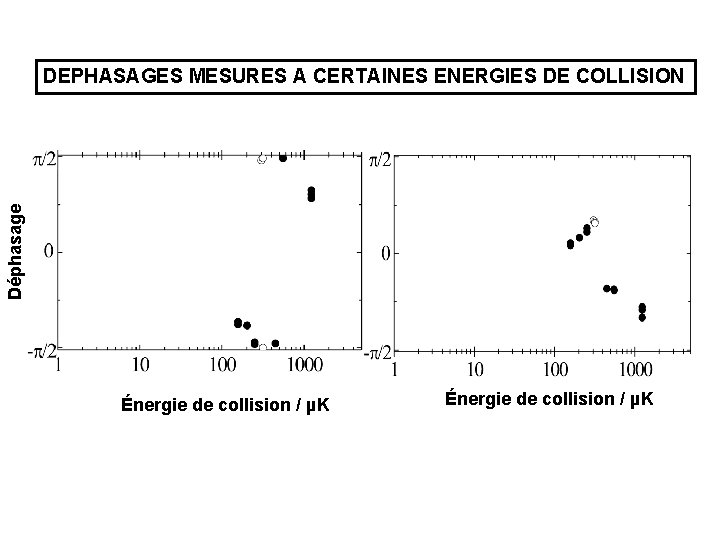
Déphasage DEPHASAGES MESURES A CERTAINES ENERGIES DE COLLISION Énergie de collision / µK

Dans la zone d’interaction : fonction d’onde indépendante de l’énergie Vers l’intérieur rin r = Déphasages expérimentaux Ondes s Ondes d (a 0) Toutes les fonctions d’ondes sont en phase en r=r in

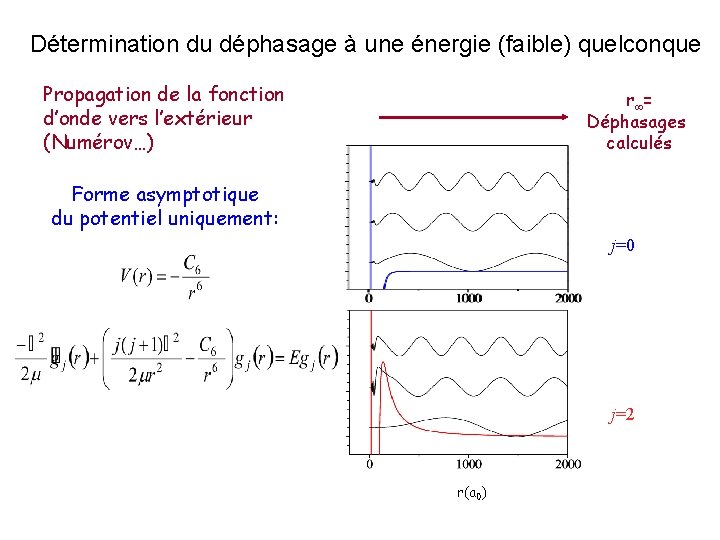
Détermination du déphasage à une énergie (faible) quelconque Propagation de la fonction d’onde vers l’extérieur (Numérov…) r = Déphasages calculés Forme asymptotique du potentiel uniquement: j=0 j=2 r(a 0)

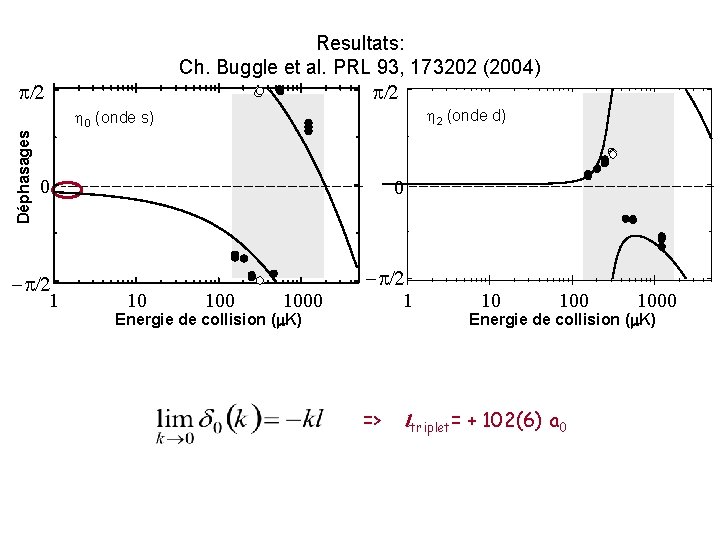
Resultats: Ch. Buggle et al. PRL 93, 173202 (2004) p/2 h 2 (onde d) Déphasages h 0 (onde s) 0 -p/2 1 0 10 1000 Energie de collision (m. K) -p/2 1 => 10 1000 Energie de collision (m. K) ltriplet= + 102(6) a 0

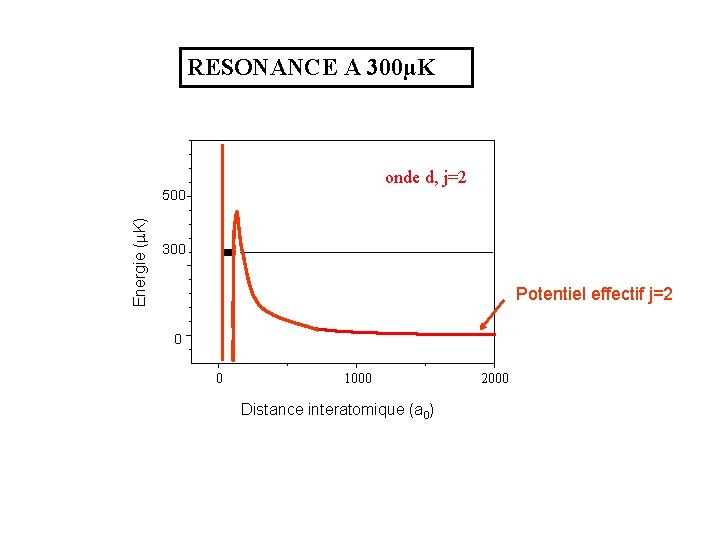
RESONANCE A 300µK onde d, j=2 Energie ( K) 500 300 Potentiel effectif j=2 0 0 1000 Distance interatomique (a 0) 2000

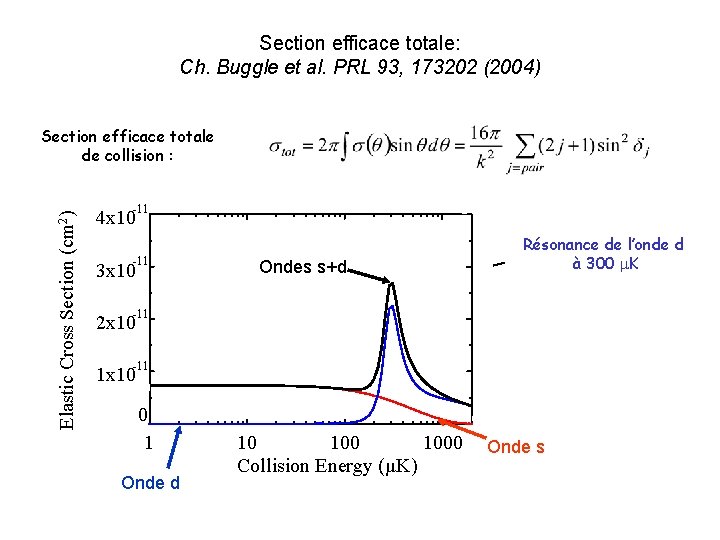
Section efficace totale: Ch. Buggle et al. PRL 93, 173202 (2004) Elastic Cross Section (cm 2) Section efficace totale de collision : -11 4 x 10 -11 3 x 10 Ondes s+d Résonance de l’onde d à 300 K -11 2 x 10 -11 1 x 10 0 1 Onde d 10 1000 Collision Energy (µK) Onde s