Mass Property Analysis The size weight surface area

Mass Property Analysis The size, weight, surface area, and other properties available from a solid model are most often part of the design constraints your design must satisfy. The following are mass property calculations available in today’s solid modelers: Volume Density Mass Surface area Centroid Moment of Inertia Product of Inertia Radii of Gyration Principal Axes Principal Moments

Volume n n Volume is the amount of three-dimensional space that an object takes up. Design engineers use this value to determine the amount of material needed to produce a part. V=Hx. Wx. L V=4 x 4 x 8 V = 128 in 3 4 4 8

Density n n Density is defined as mass per unit volume. Density is different for every material and can be found in a machinist handbook.

Mass n n Mass is the amount of matter in an object or the quantity of the inertia of the object. Many materials are purchased by weight; to find weight, we need the mass. Polypropylene has a density of. 035 lbs/in 3 Mass = Volume x Density Mass = 128 in 3 x. 035 lbs/in 3 Using the volume from the previous example. (128 in 3) Mass = 4. 48 lbs.

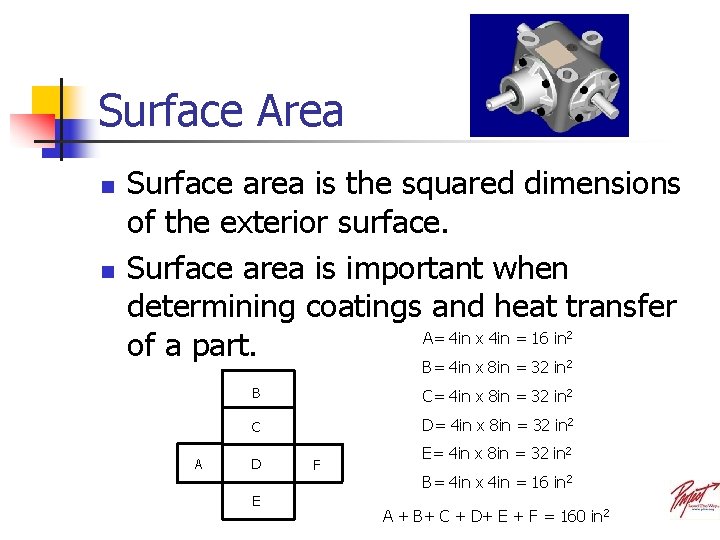
Surface Area n n Surface area is the squared dimensions of the exterior surface. Surface area is important when determining coatings and heat transfer A= 4 in x 4 in = 16 in of a part. 2 B= 4 in x 8 in = 32 in 2 A B C= 4 in x 8 in = 32 in 2 C D= 4 in x 8 in = 32 in 2 D E F E= 4 in x 8 in = 32 in 2 B= 4 in x 4 in = 16 in 2 A + B+ C + D+ E + F = 160 in 2

Centroid n n n A 3 D point defining the geometric center of a solid. Do not confuse centroid with the center of gravity. The two only exist at the same 3 D point when the part has uniform geometry and density.

Moments of Inertia n n An object’s opposition to changing its motion about an axis. This property is most often used when calculating the deflection of beams. = Integral (Calculus) I = Moments of Inertia r = Distance of all points in an element from the axis p = Density of the material d. V= Division of the entire body into small volume units.

Products of Inertia n n Is similar to moments of inertia only that products of inertia are relative to two axes instead of one. You will notice an XY, YZ, or ZX after the I symbol when defining products of inertia compared to moments of inertia.

Radii of Gyration n A dimension from the axis where all mass is concentrated, and will produce the same moment of inertia. K = Radius of gyration about an axis M = Mass I = Moments of inertia

Principal Axes n The lines of intersection created from three mutually perpendicular planes, with the three planes point of intersection at the centroid of the part. The X, Y, and Z axes show the principal axes of the ellipsoid.

Principal Moments n Principal moments are the moments of inertia related to the principal axes of the part.