Mass of the Vector Meson in Quantum Chromodynamics

Mass of the Vector Meson in Quantum Chromodynamics in the limit of large number of colors Rahul Patel With Carlos Prays and Ari Hietanen Mentor: Dr. Rajamani Narayanan Department of Physics Florida International University

OUTLINE • Quantum Chromodynamics • Feynman Path Integral (Quantum) • Parallel Transport (Gauge Theory) - Abelian (EM) and Non-Abelian (Color) • Particle Propagation - Meson and Quark propagation - Vector Meson Propagation • Computer Simulation

Quarks and Gluons Quarks • Elementary particles constituting most matter in universe • Six different quarks • Combinations of these quarks form composite particles: 1) Baryons (3 quark combination): ex: Protons, Neutrons 2) Mesons (quark, anti-quark combo): ex: pion, rho • Combinations must produce colorless particles (due to Gauge symmetry) Gluons • Messenger particles between quarks

Quantum Chromodynamics (QCD) • Study of interaction between quarks and gluons • Interaction causes Strong Force • Analogy: Electromagnetic force: photon field interacting with electrons and protons – only 1 field. Strong force: Gluon field interacts with quarks – 8 fields defined by color names (red, blue, green, etc. ) – Confinement!!! • N: refers to number of fields • N 2 - 1 particles of that field • This project studies QCD in more than 3 colors (N) Final goal to set N infinity.

Summary thus Far… Goal: To calculate the mass of a ρ particle at zero quark mass at Large N (color fields) and 4 dim. Large N : • Large N : Results simplify for SU(N) where N ∞ • Do not expect any qualitative difference between N = 3 and N = infinite • QCD results obtained by setting N = 3 What is rho (ρ)? • Subnuclear particle made up of two quarks • Excited state of meson but a lot heavier • pi meson mass goes to zero when quark mass goes to zero. . WHAT ABOUT ρ?

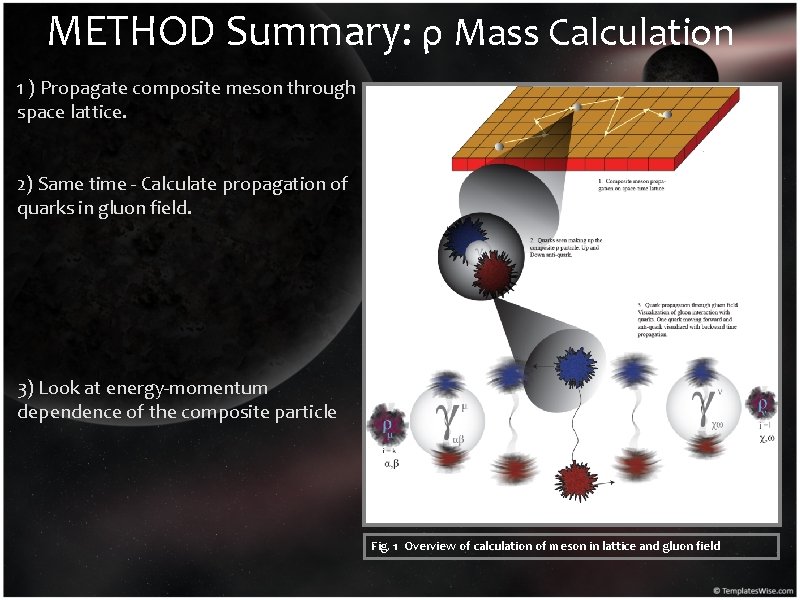
METHOD Summary: ρ Mass Calculation 1 ) Propagate composite meson through space lattice. 2) Same time - Calculate propagation of quarks in gluon field. 3) Look at energy-momentum dependence of the composite particle 4) E 2 = (mc 2)2 + (pc)2 Note: i) Particle being studied is ρ meson ii) 1 up and 1 anti – down quark Fig. 1 Overview of calculation of meson in lattice and gluon field

Lattice Gauge Theory • Smooth, infinite continuous space is divided into finitely chopped up pieces cells Why? • Purpose: Prevent infinities in calculation • Quantum Field theory: - Continuous space-time ∞ particles (explain field theory) - Get rid of ∞ particles by eliminating ∞ space - Make it finite but large • Vary lattice size to and obtain thermodynamic limit Fig. 1 Visualization of propagation of composite particle through space lattice

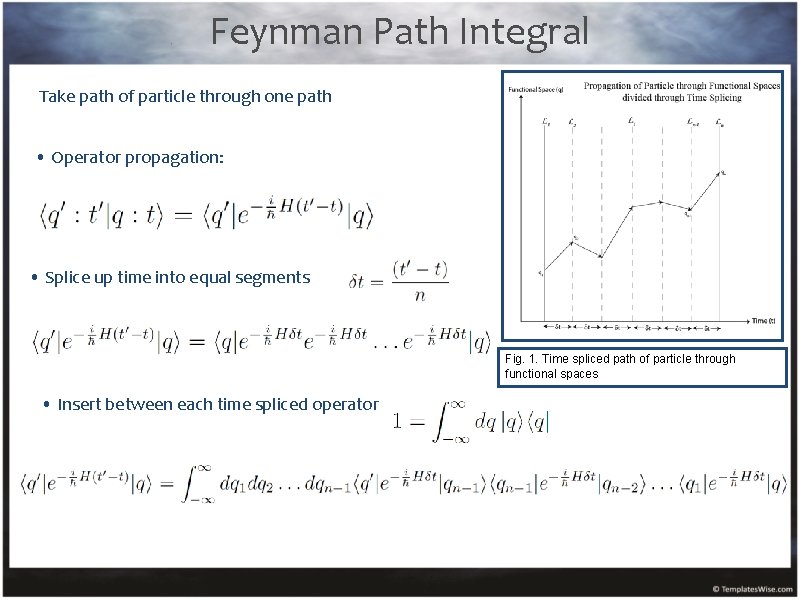
Feynman Path Integral Take path of particle through one path • Operator propagation: • Splice up time into equal segments Fig. 1. Time spliced path of particle through functional spaces • Insert between each time spliced operator

• Feynman evaluated it • After skipping tons of steps and introducing the Lagrangian : -- time evolution can be written in integral form: • Introduce time transformation:

• Went from operator to integral form – all that trouble why? • Kept Feynman busy – and is easier to compute • All possible paths (ALL OF THEM) must be taken into account • Path amplitudes nullified if dissproportionate to 1/h factor

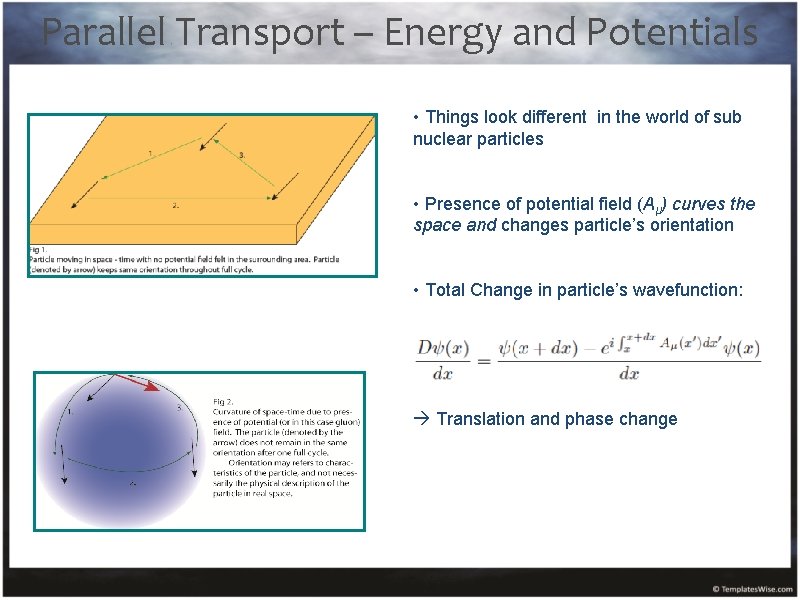
Parallel Transport – Energy and Potentials • Things look different in the world of sub nuclear particles • Presence of potential field (Aμ) curves the space and changes particle’s orientation • Total Change in particle’s wavefunction: Translation and phase change

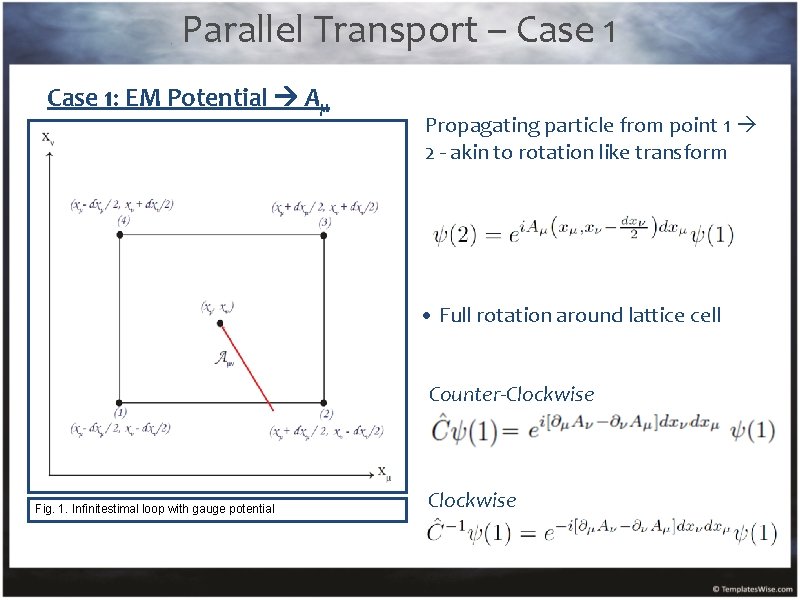
Parallel Transport – Case 1: EM Potential Aμ Propagating particle from point 1 2 - akin to rotation like transform • Full rotation around lattice cell Counter-Clockwise Fig. 1. Infinitestimal loop with gauge potential Clockwise

• Full change in wavefunction: • Where: is the Field Strength Tensor • Taylor expanding gives us: • Replacing μ, ν = 0, 1, 2, 3 in Gauge Field (1 time, 3 space) sum over all combinations • Potentials take on form of electromagnetic potentials and by increasing number of lattice cells, energy change derived:

Parallel Transport – Case 2: Non-Abelian Gauge Potential Aμ as matrix • Repeat propagation of particle through small loop • Counter-Clockwise and Clockwise propagation • New Strength Tensor Extra commutator indicative of non-Abelian nature

Parallel Transport – N dim Potentials • Aμν : N x N Hermitian matrix • Aaν (x) where a: [1, N 2 -1] N determines type of field and number of fields - N = 2: Weak Field, N = 3: Strong Color Field • At large N, commutator overpowers other terms – Field to Field interaction • New Action given by: • Path integral for non – Abelian gauge potential: • Need to be able to propagate this through the lattice

• Phase change through Gauge field replaced by unitary matrices Traceless: • Propagation in clockwise and counter-clockwise direction of original finite cell replaced by unitary matrices: • Partition function of Lattice QCD:

METHOD Summary: ρ Mass Calculation 1 ) Propagate composite meson through space lattice. 2) Same time - Calculate propagation of quarks in gluon field. 3) Look at energy-momentum dependence of the composite particle Fig. 1 Overview of calculation of meson in lattice and gluon field

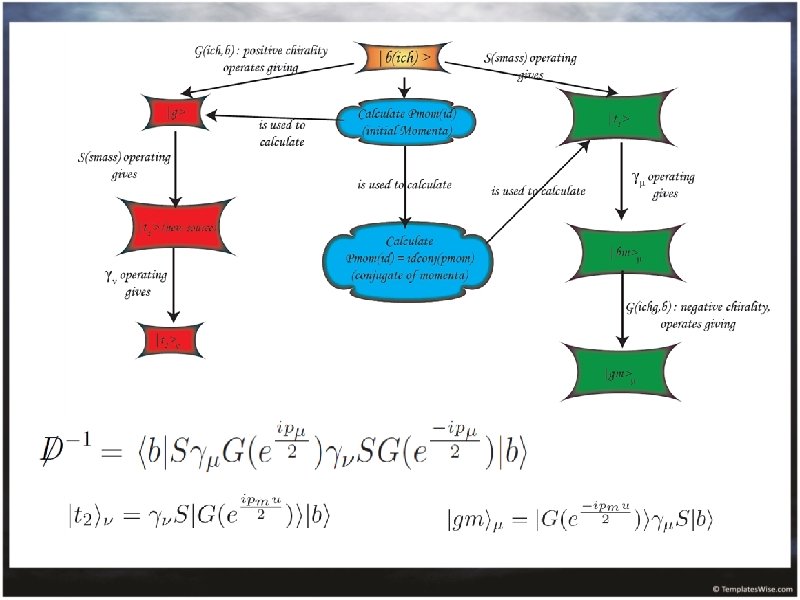
Meson and Quark Propagation through Gluon Field • Relativistic sister of Schrödinger equation: Dirac operator: where • Propagator for general quark: Propagation through lattice (d. U) given by inverse Dirac operator: • Need to specify type of particle ρ meson is vector particle with bilinear transformation • Insert γμ for vector meson

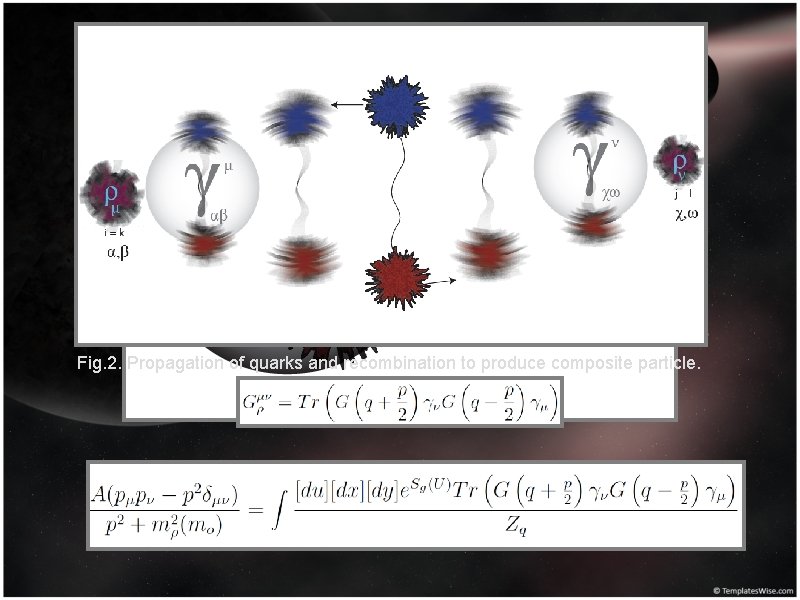
Vector Meson Propagation • Propagator for particle in momentum space through Fourier transform to obtain energy • Inversely proportional to Dirac Operator • Trace of propagator gives propagational amplitude of quarks in gluon field

Fig. 2. Propagation of quarks and recombination to produce composite particle.

Calculation • Code developed to obtain mass calculation • Unitary matrix array (7 –dim) , [3 space, 1 time, motion, matrix coordinates] • Lattice thermalized • Initial momentum ; n = 2, 3, 4, 5, 6 • Calculate Propagational amplitude: • Smear operator (Inverse of gauge laplacian) spread given wavefunction for maximum overlap with physical state

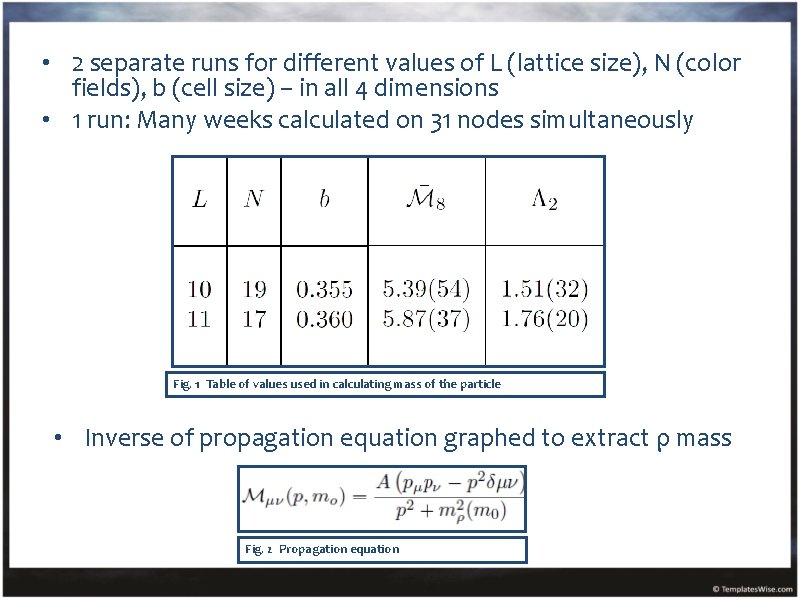
• 2 separate runs for different values of L (lattice size), N (color fields), b (cell size) – in all 4 dimensions • 1 run: Many weeks calculated on 31 nodes simultaneously Fig. 1 Table of values used in calculating mass of the particle • Inverse of propagation equation graphed to extract ρ mass Fig. 2 Propagation equation

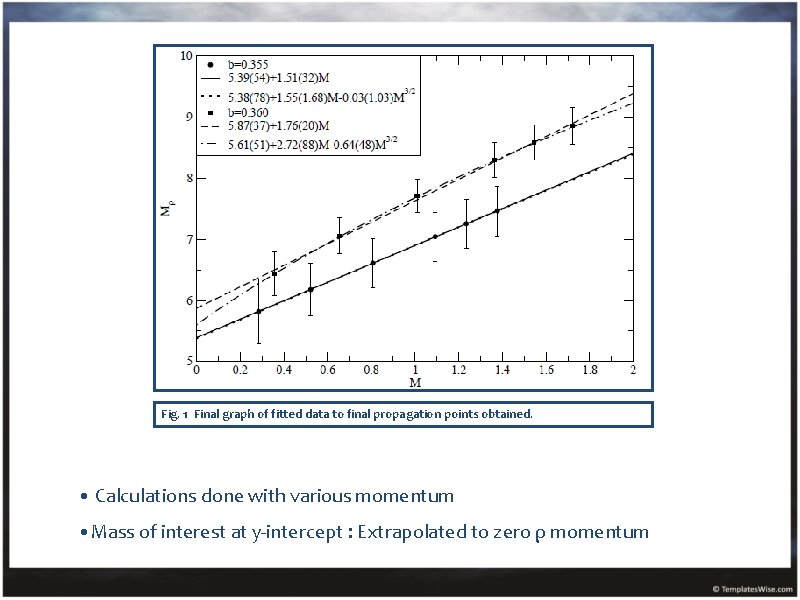
Fig. 1 Final graph of fitted data to final propagation points obtained. • Calculations done with various momentum • Mass of interest at y-intercept : Extrapolated to zero ρ momentum

RESULTS • Final results for the mass of the rho particle while taking the mass of the quarks to be zero is: 1082 +/- 70 Me. V for N ∞ • The experimental value is: 775. 5 +/- 0. 4 Me. V • Final results still correct by taking above factors into account • Results - Published in Physics Letters B 674(2009): 80 -82. “The vector meson mass in the large N limit of QCD. ” ar. Xiv: 0901. 3752 [hep-lat]

REFERENCES • Cheng, Ta-Pei and Li, Ling-Fong. Gauge Theory of Elementary Particle Physics. New York: Oxford UP, USA, 1988 • M. Creutz, Quarks, Gluons, and Lattices, Cambridge University Press, 1985 • M. Leon, Particle Physics: An Introduction, Academic Press, 1973 • R. Narayanan, H. Neuberger, Phys. Lett. B 616 (2005) 76 -84 • J. Marion, S. Thornton, Classical Dynamics of Particles and Systems, Thomson Brooks/Cole, 2004 • G. Arfken, H, Weber, Mathematical Methods for Physicists 6 e. , Elevier Academic Press, 2005 • A. V. Manohar, in Les Houches 1997, Probing the standard model of particle interactions, Pt. 2, ar. Xiv: hep-ph/9802419

Thank You • • • Dr. Rajamani Narayanan Carlos Prays Dr. Ari Hietenan Richard Galvez Dr. Rodriguez, Ricardo Leante All the wonderful people in this room.