MASS DENSITY AND VOLUME AREAS OF SHAPES L

MASS DENSITY AND VOLUME

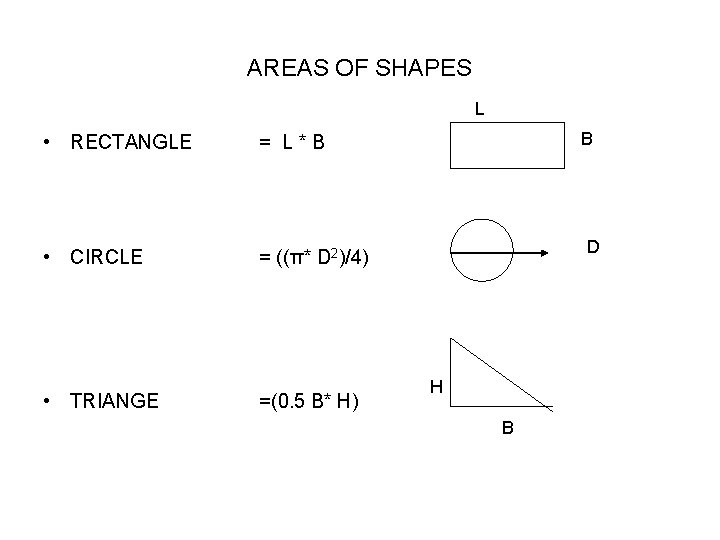
AREAS OF SHAPES L • RECTANGLE = L*B • CIRCLE = ((π* D 2)/4) • TRIANGE =(0. 5 B* H) B D H B

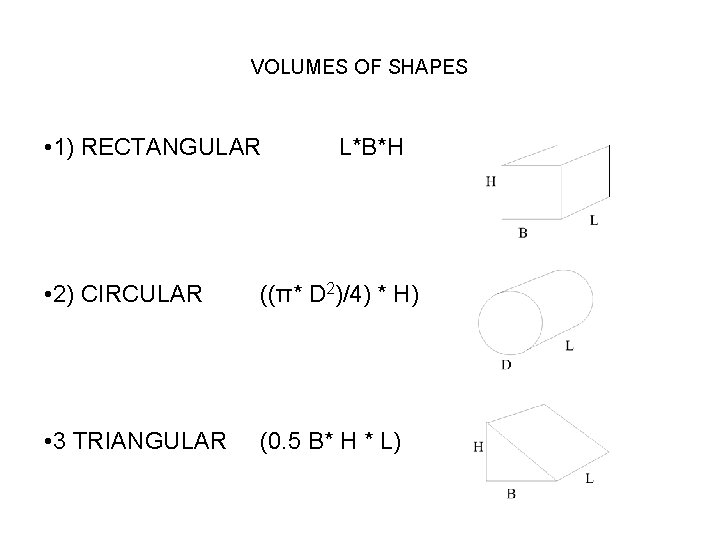
VOLUMES OF SHAPES • 1) RECTANGULAR L*B*H • 2) CIRCULAR ((π* D 2)/4) * H) • 3 TRIANGULAR (0. 5 B* H * L)

THE CONCEPT OF MASS , DENSITY AND LOADING • DENSITY IS THE MASS OF AN OBJECT / m 3 • • MASS =VOLUME * DENSITY =Kg • LOAD= KG * 9. 81 = NEWTONS • LOAD IN KN = NEWTONS /1000

DENSITY • DIFFERENT MATERIALS HAVE DIFFERENT DENSITIES AND DIFFERENT MASSES / VOLUME • WATER =1000 Kg / m 3 • CONCRETE =2400 Kg / m 3 • STEEL =6800 Kg / m 3 • WOOD =1650 Kg / m 3

Rectangular shapes

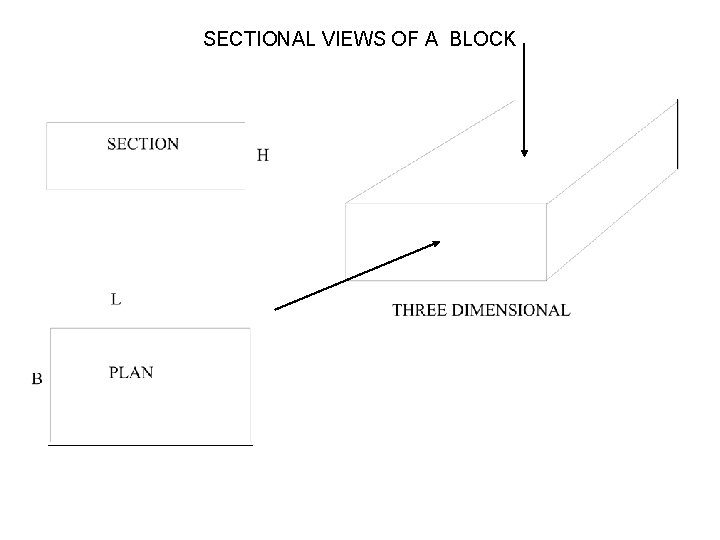
SECTIONAL VIEWS OF A BLOCK

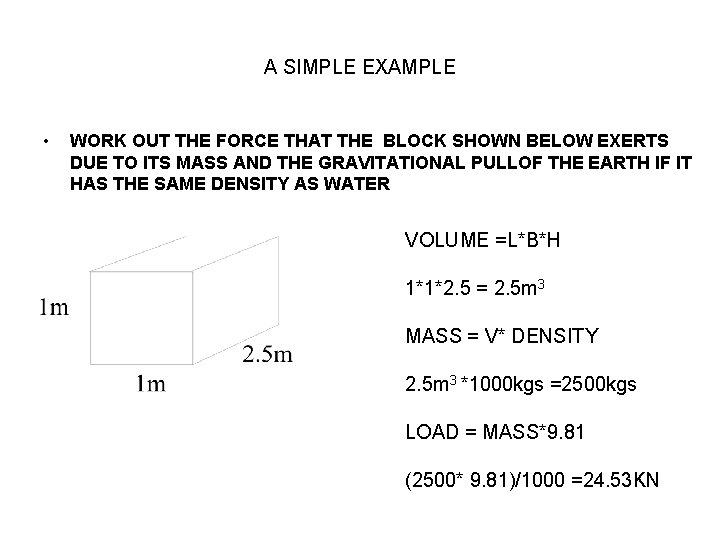
A SIMPLE EXAMPLE • WORK OUT THE FORCE THAT THE BLOCK SHOWN BELOW EXERTS DUE TO ITS MASS AND THE GRAVITATIONAL PULLOF THE EARTH IF IT HAS THE SAME DENSITY AS WATER VOLUME =L*B*H 1*1*2. 5 = 2. 5 m 3 MASS = V* DENSITY 2. 5 m 3 *1000 kgs =2500 kgs LOAD = MASS*9. 81 (2500* 9. 81)/1000 =24. 53 KN

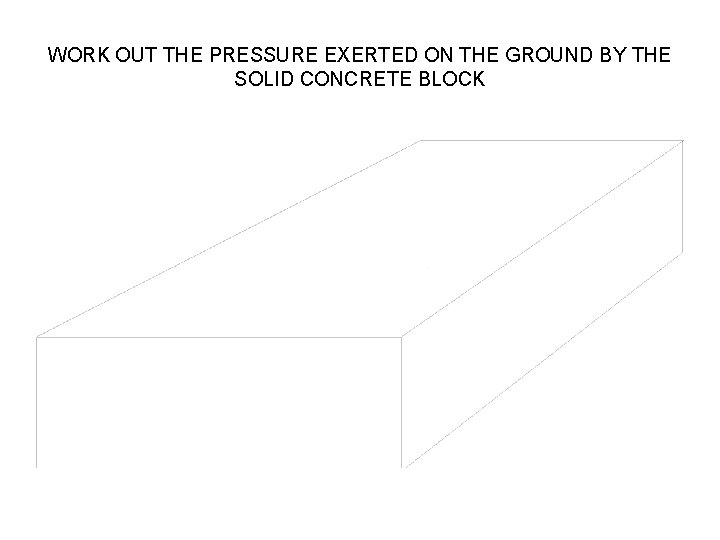
WORK OUT THE PRESSURE EXERTED ON THE GROUND BY THE SOLID CONCRETE BLOCK

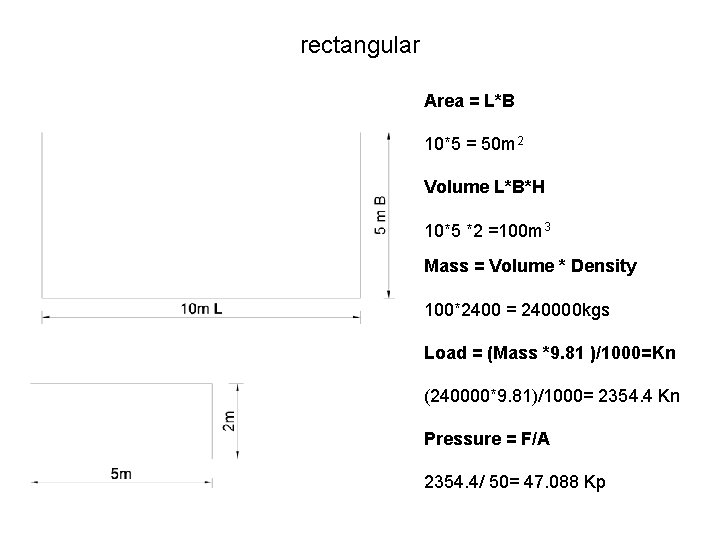
rectangular Area = L*B 10*5 = 50 m 2 Volume L*B*H 10*5 *2 =100 m 3 Mass = Volume * Density 100*2400 = 240000 kgs Load = (Mass *9. 81 )/1000=Kn (240000*9. 81)/1000= 2354. 4 Kn Pressure = F/A 2354. 4/ 50= 47. 088 Kp

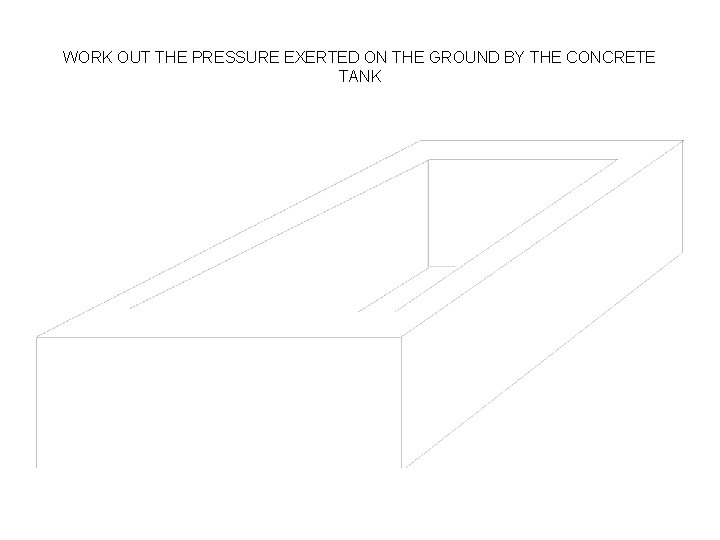
WORK OUT THE PRESSURE EXERTED ON THE GROUND BY THE CONCRETE TANK

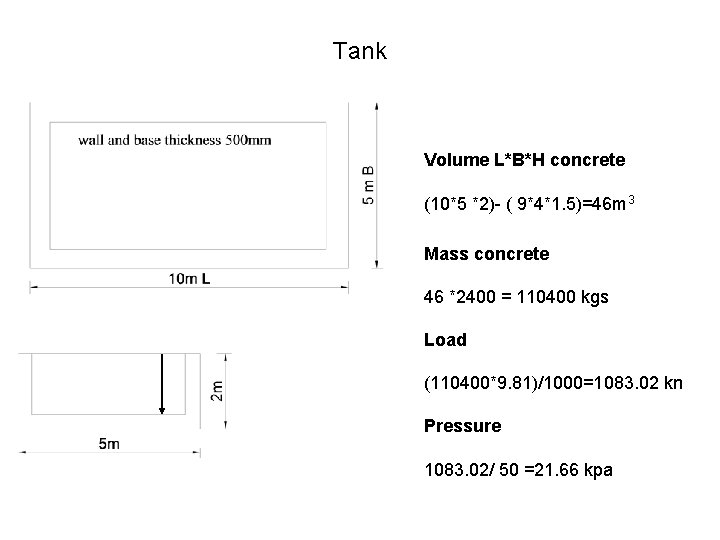
Tank Volume L*B*H concrete (10*5 *2)- ( 9*4*1. 5)=46 m 3 Mass concrete 46 *2400 = 110400 kgs Load (110400*9. 81)/1000=1083. 02 kn Pressure 1083. 02/ 50 =21. 66 kpa

WORK OUT THE PRESSURE EXERTED ON THE GROUND BY THE CONCRETE TANK FILLED WITH WATER

Tank filled with water Volume L*B*H concrete (10*5 *2)- ( 9*4*1. 5)=46 m 3 Mass concrete 46 *2400 = 110400 kgs Volume water ( 9*4*1. 5)=54 m 3 Mass of water 54*1000=54000 kgs Load ((110400+54000)*9. 81)/1000=16 Pressure = 1612. 76/ 50 = 32. 26

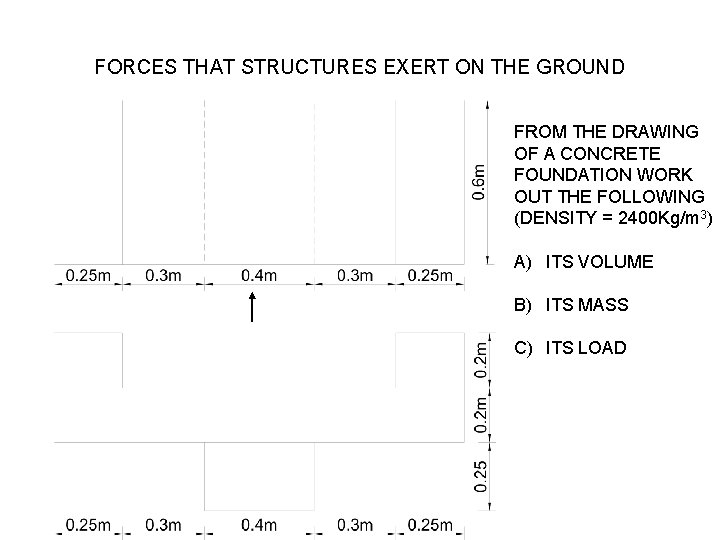
FORCES THAT STRUCTURES EXERT ON THE GROUND FROM THE DRAWING OF A CONCRETE FOUNDATION WORK OUT THE FOLLOWING (DENSITY = 2400 Kg/m 3) A) ITS VOLUME B) ITS MASS C) ITS LOAD

MODEL ANSWER • Vol = (1. 5* 0. 4*0. 6) – (1 *0. 6 *0. 2)+ ( 0. 4*0. 6*0. 25)= 0. 3 m 3 • Mass = 0. 3 *2400= 720 kgs • Load = ( 720*9. 81)/ 1000 = 7. 06 kn

Cylinders

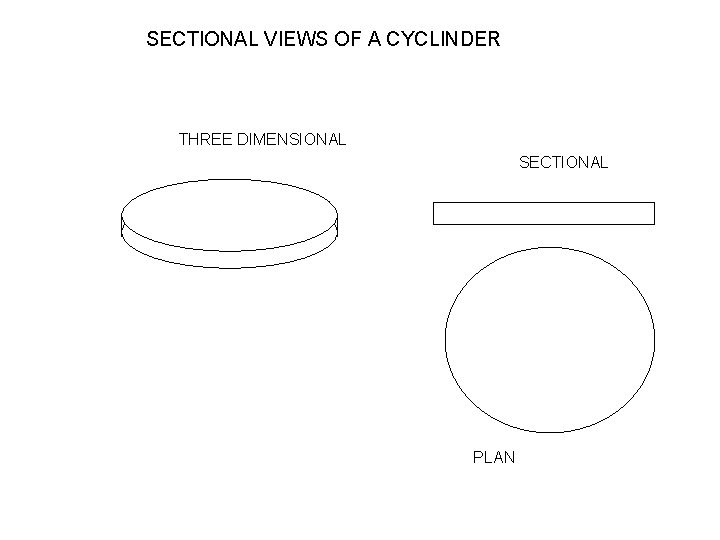
SECTIONAL VIEWS OF A CYCLINDER THREE DIMENSIONAL SECTIONAL PLAN

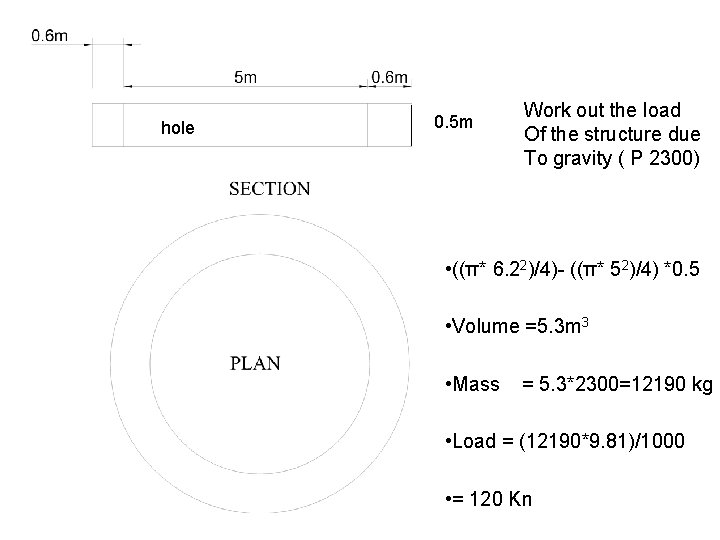
hole 0. 5 m Work out the load Of the structure due To gravity ( P 2300) • ((π* 6. 22)/4)- ((π* 52)/4) *0. 5 • Volume =5. 3 m 3 • Mass = 5. 3*2300=12190 kg • Load = (12190*9. 81)/1000 • = 120 Kn

Diameter 3. 5 m

• • • A circular tank is to be filled with sand density 1234 find the pressure the tank exerts on the ground A) when empty B) when fill of sand xsa cylinder = 28. 3 m 2 vol = 28. 3*3=84. 9 xsa hole = 23. 76 m 2 vol = 23. 76*2. 75=65. 34 Total vol concrete = 84. 9 - 65. 34 = 19. 56 m 3 Mass = 19. 56 * 2400 = 46944 kgs Load =( 46944*9. 81)/ 1000= 460. 52 kn Pressure = 460. 52 / 28. 3 = 16. 27 kpa Mass sand = 65. 34 *1234 = 80629. 56 Load = (80629. 56*9. 81)/1000=790. 97 kn Pressure = (460. 52+790. 97)/ 28. 3=44. 22 kpa

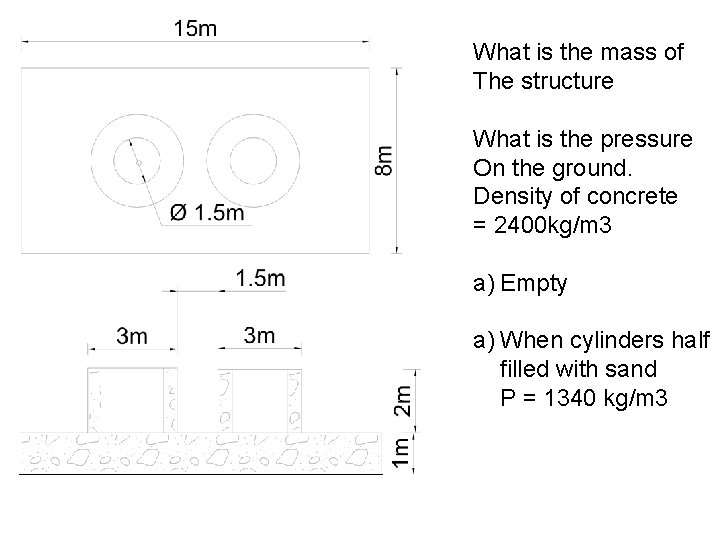
What is the mass of The structure What is the pressure On the ground. Density of concrete = 2400 kg/m 3 a) Empty a) When cylinders half filled with sand P = 1340 kg/m 3

Rec V= 15 *8 *1 = 120 m 3 CIR V= (((π * 3 2 /4 )-(π * 1. 5 2 /)4 ))*2 ) * 2) = 21. 21 m 3 MASS CON = 141. 21* 2400 = 338904 kgs LOAD = (338904 *9. 81)/1000= 3324. 65 kn PRESSURE = 3324. 65 /(8*15 ) = 27. 71 SAND V = (π * 1. 5 2 /)4 )*2 = 3. 53 m 3 LOAD = (3. 53 *1340 * 9. 81 )/1000= 46. 4 KN TOTAL PRESSURE = (3324. 65+46. 4) /(8*15 )= 28. 1

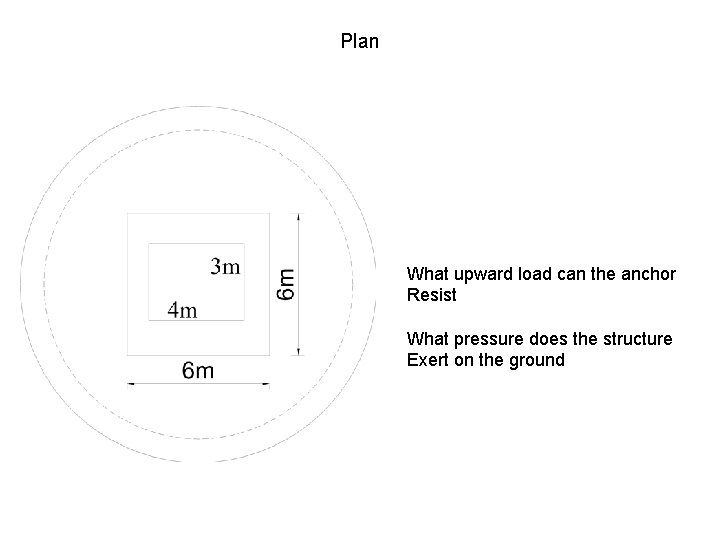
Plan What upward load can the anchor Resist What pressure does the structure Exert on the ground

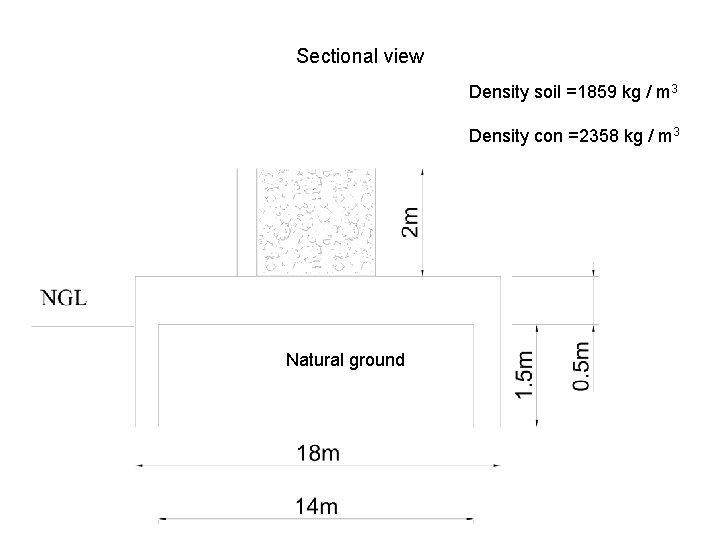
Sectional view Density soil =1859 kg / m 3 Density con =2358 kg / m 3 Natural ground

Model answer • Volume of base = (π* 182)/4)*2)-(π* 142)/4)*1. 5)= 278. 03 • Volume of column = (6*6*2 ) – (4*3*2) = 48 • Volume of sand = (4*3*2) =24 • • • Total volume = 278. 03+48 = 326. 03 Mass empty = 326. 03 *2358 =768778. 74 Mass sand = 24 * 1859 = 44616 Total mass = 813394. 74 kgs Load = (813394. 74 *9. 81) /1000 = 7979. 40 kn Pressure = 7979. 40)/(π* 142)/4)=51. 83

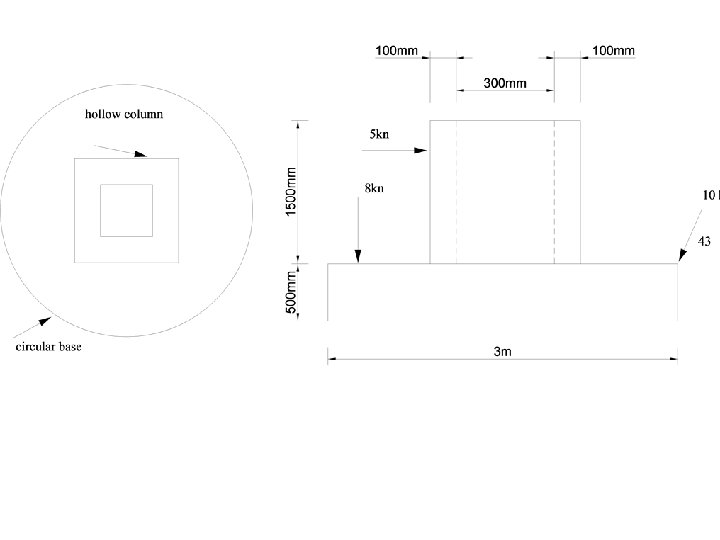
Examples • A concrete footing consists of a circular base and a hollow square column. The base has a diameter of 3, 0 m and is 500 mm thick. The external dimensions of the 1, 5 m high column are 500 mm x 500 mm with a wall thickness of 100 mm. Concrete has a density of 2 400 kg/m 3 and the footing is loaded as shown. • Calculate the pressure exerted by the concrete footing on the ground below.

3 d view

• QUESTION ONE (12 marks) • Vbase = x 32 x 0, 5 = 3, 534 m 3 (1 mark) • Vcol = [(0, 5 x 0, 5) – (0, 3 x 0, 3)] x 1, 5 = 0, 24 m 3 (1 mark) • Vtot = 3, 774 m 3 • Wconc = 2400 x 3, 774 x 9, 81 / 1000 = 88, 856 k. N (2 marks) • Total downward load = 88, 856 + 10 sin 43 + 8 = 103, 676 k. N (2 marks) • Area = x 32 = 7, 069 m 2 (2 marks) • Pressure = Force / Area = 103, 676 / 7, 069 = 14, 666 k. Pa (2 marks)

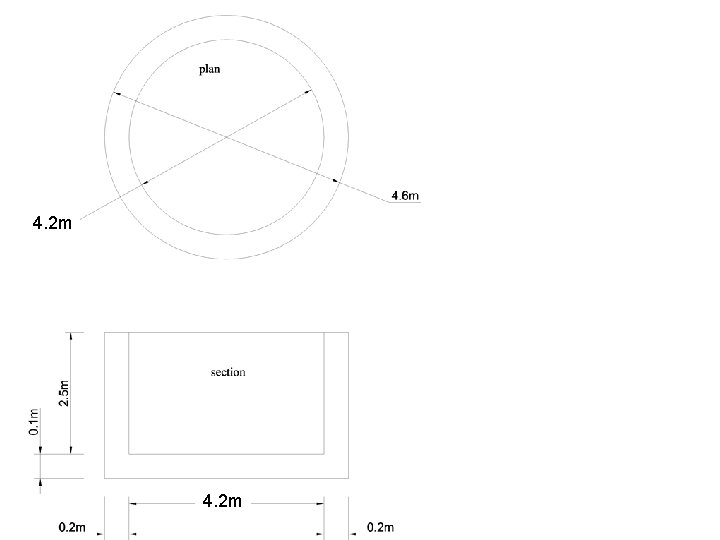
Example 2 • The drawing BELOW shows the plan view and sectional view of a circular concrete tank if the density of concrete and water is 2345 kg/ m 3 and 1000 kg/ m 3 respectively calculate the following. • The resultant load of the structure • the pressure exerted by the tank on the ground when it is filled with water

4. 2 m

• • Vol cylinder = (( π* 4. 62)/4 )*2. 6)) = 43. 21 Vol hole = (( π* 4. 22)/4 )*2. 5)) = 34. 61 Vol concrete = 43. 21 – 34. 64 = 8. 57 Load =( 8. 57 * 2345 * 9. 81 )/1000 = 197. 15 kn • Vol w = 34. 64 • Load = 34. 64 *9. 81 = 339. 82 • Tot load = 197. 15 + 339. 82 = 536. 97 • Pressure 536. 97 /(( π* 4. 62)/4 )= 16. 62 kpa