MASONRY ARCH BRIDGES LOAD CARRYING CAPACITY Simply Supported

MASONRY ARCH BRIDGES LOAD CARRYING CAPACITY

Simply Supported Beam Supporting single point load

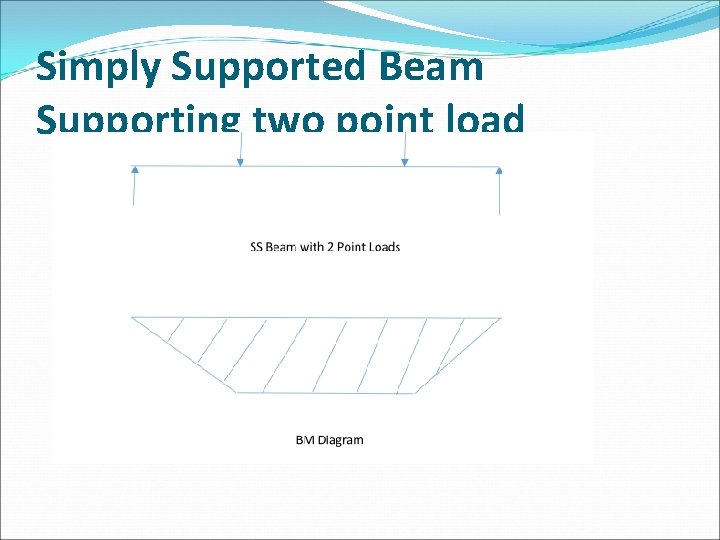
Simply Supported Beam Supporting two point load

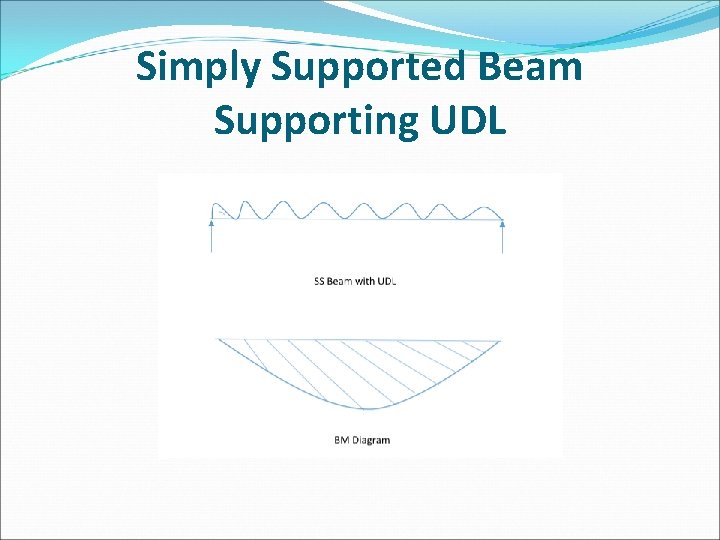
Simply Supported Beam Supporting UDL

Suspension cable with single point load

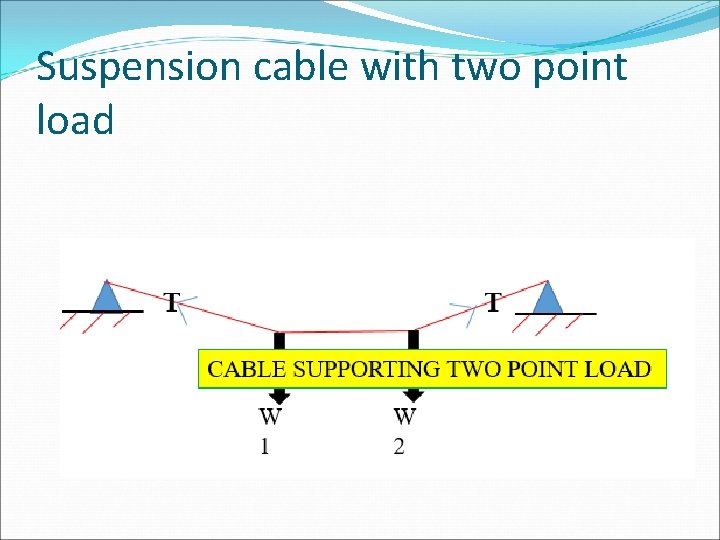
Suspension cable with two point load

Suspension cable with UDL load

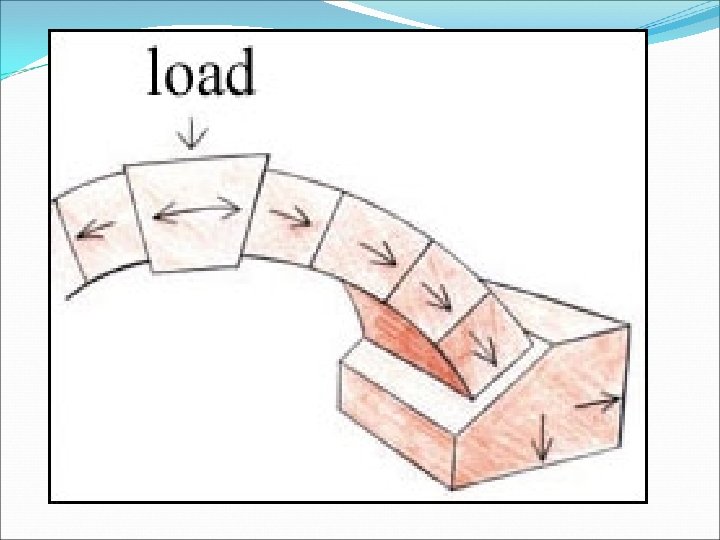
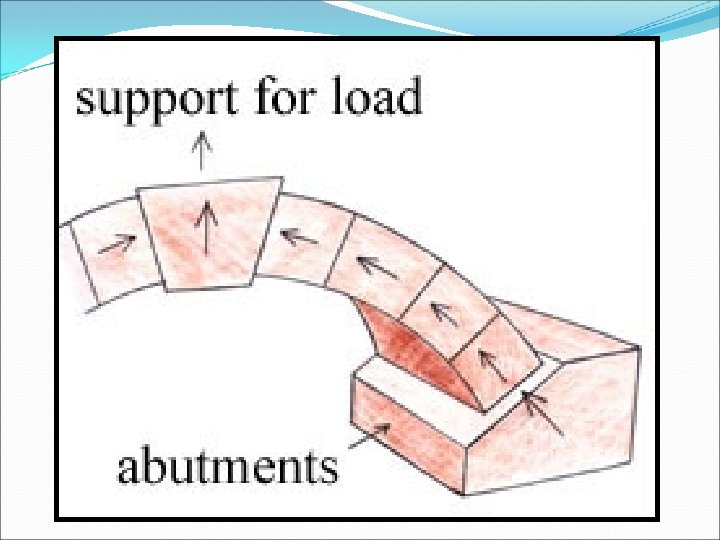
True Arch supporting single point Load

True Arch supporting Two point Load

True Arch supporting UD Load

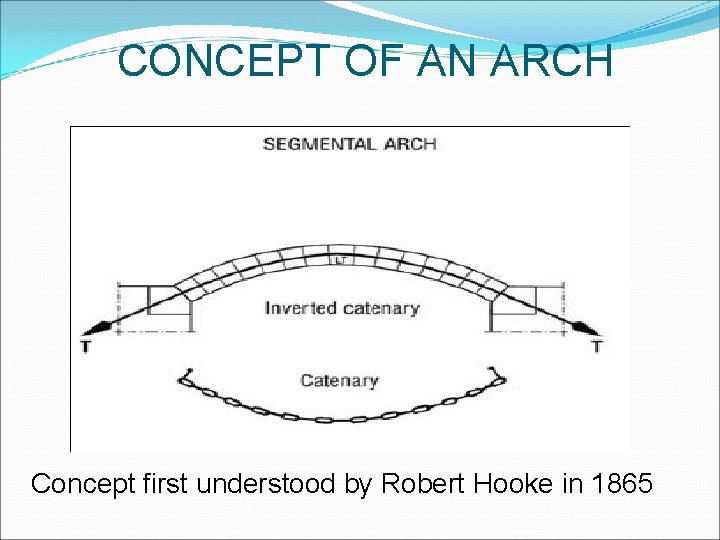
CONCEPT OF AN ARCH Concept first understood by Robert Hooke in 1865

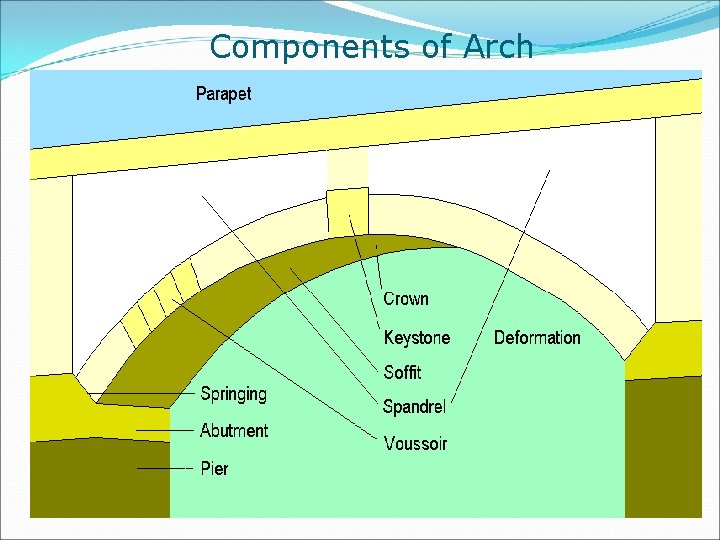
Components of Arch

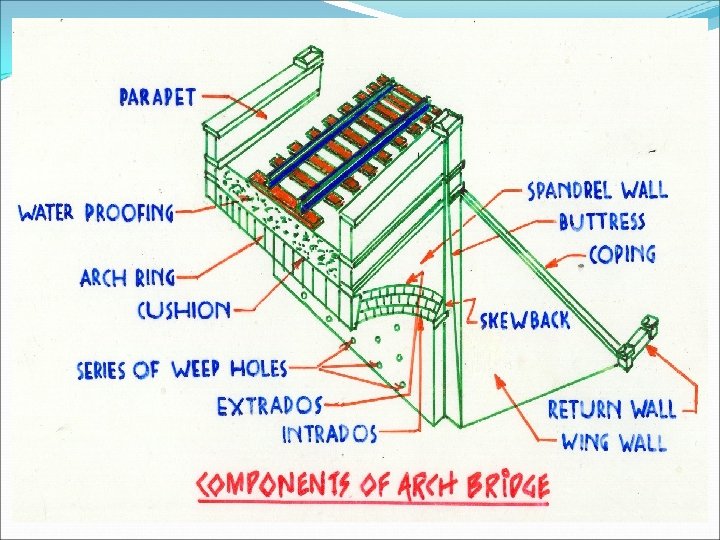
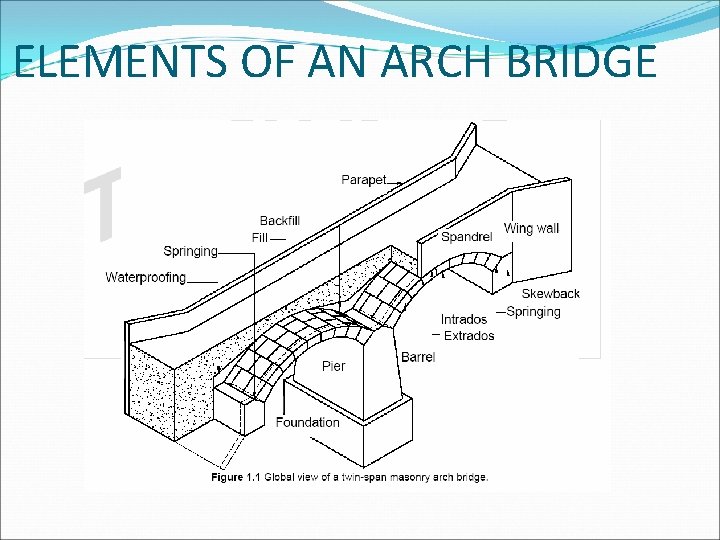
ELEMENTS OF AN ARCH BRIDGE

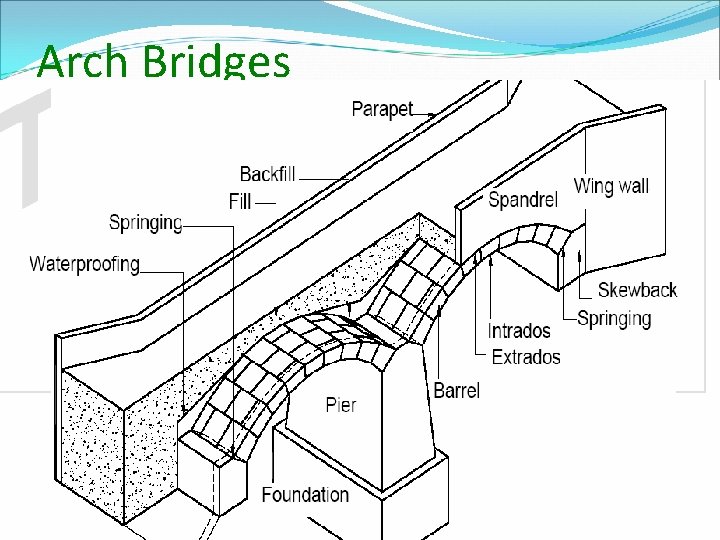
Arch Bridges

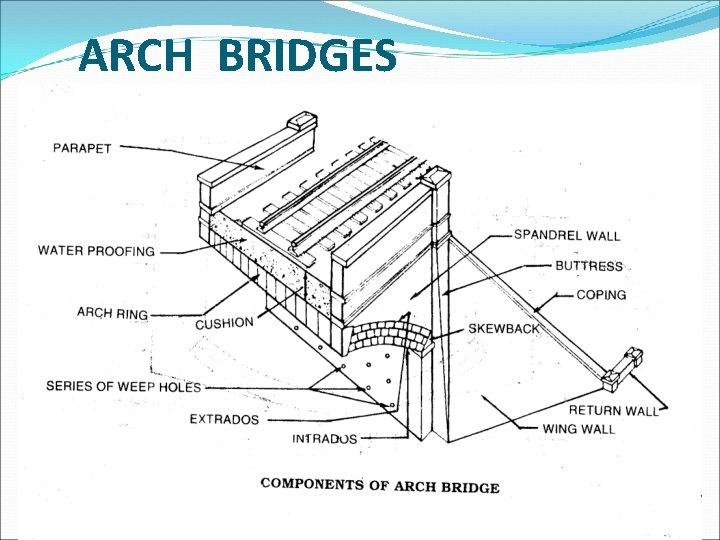
ARCH BRIDGES

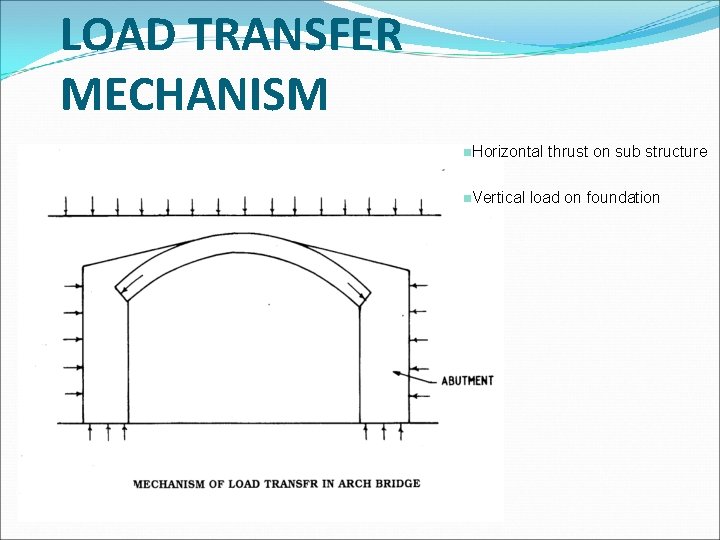
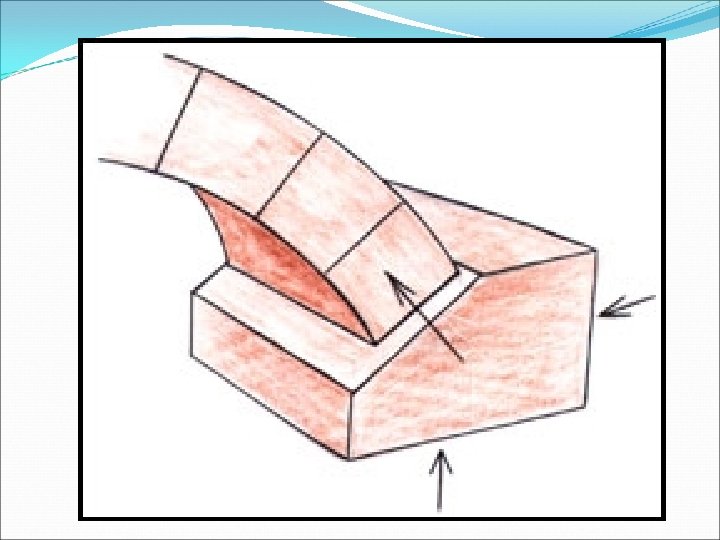
LOAD TRANSFER MECHANISM n. Horizontal n. Vertical thrust on sub structure load on foundation

Analysis of Simple structures Analysis of any structure is based on Equilibrium condition of forces For 3 dimensional structures Six conditions ∑ Fx = 0, ∑ Fy = 0, ∑ Fz = 0, ∑ Mx = 0, ∑ My = 0, ∑ Mz = 0, For 2 dimensional structures 3 conditions ∑ Fx = 0, ∑ Fy = 0, ∑ Mz = 0,

Determinacy of structures Structure is determinate if no. of unknown forces (member forces/support forces) are equal to equilibrium conditions. Structure is indeterminate if no. of unknown forces (member forces/support forces) are more than equilibrium conditions. Stability of any structure is directly proportional to Indeterminacy. In real life situation, most of the structure are indeterminate

If the indeterminacy is zero, structure is just stable and safe. If indeterminacy is less than zero (-ve), structure will fail under load.

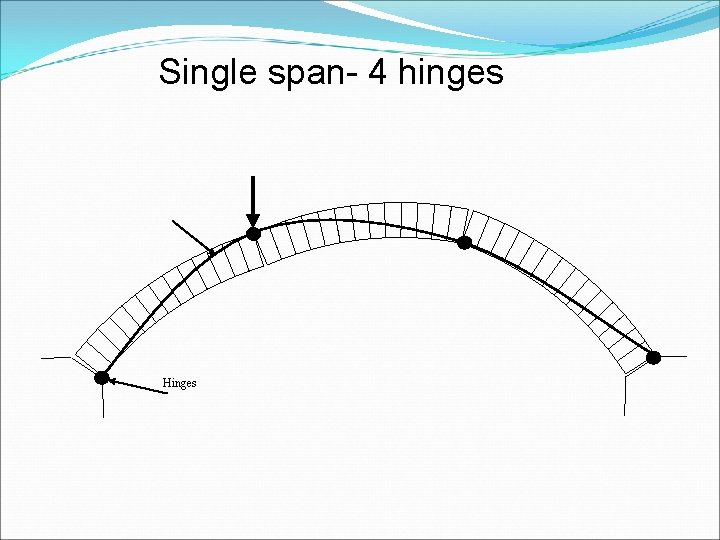
Single span- 4 hinges Hinges

FAILURE UNDER LOAD

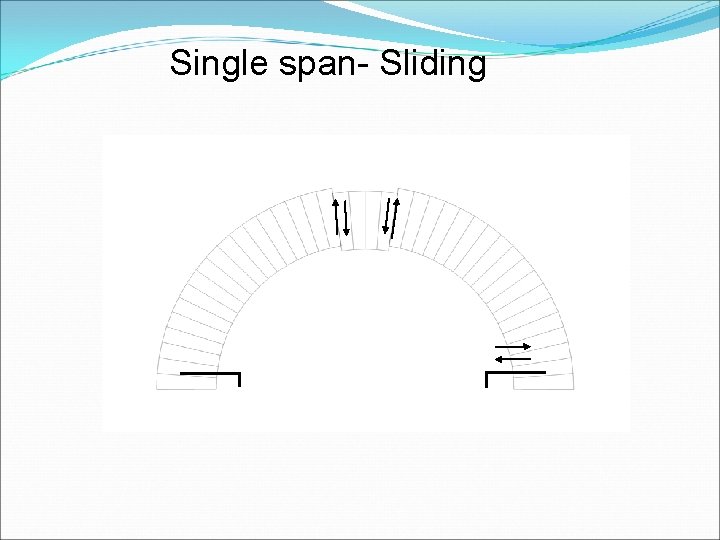
Single span- Sliding

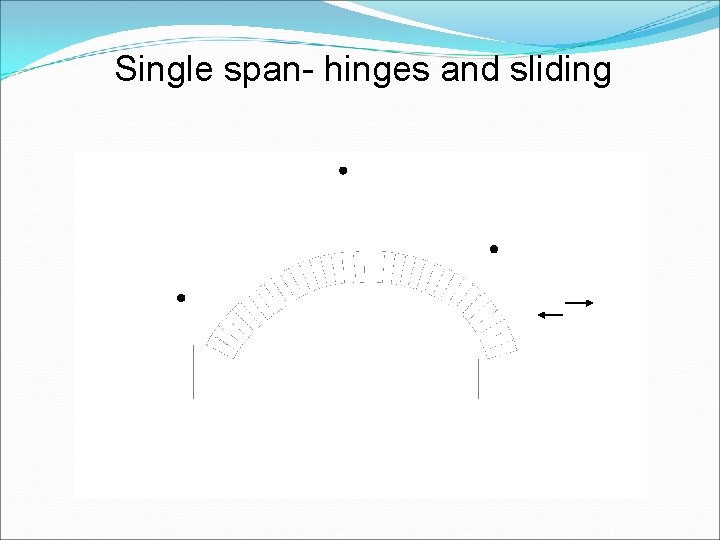
Single span- hinges and sliding

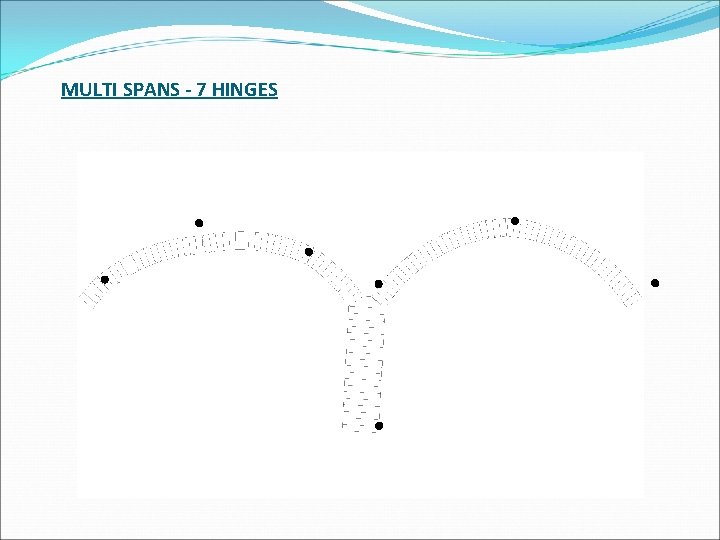
MULTI SPANS - 7 HINGES

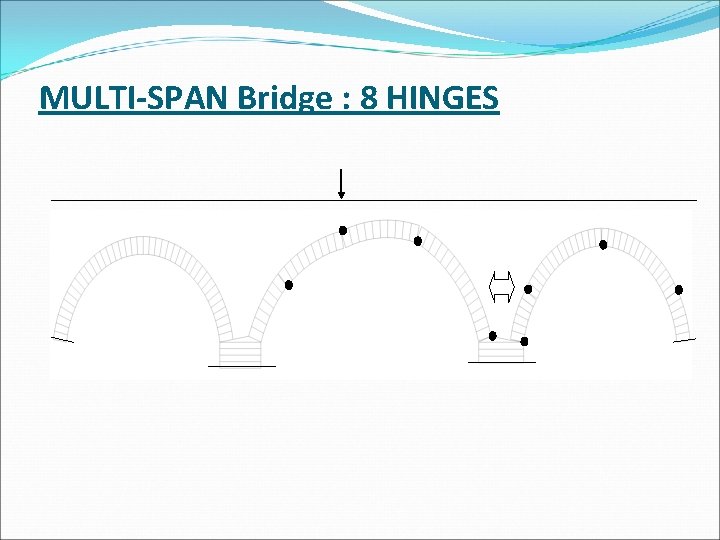
MULTI-SPAN Bridge : 8 HINGES

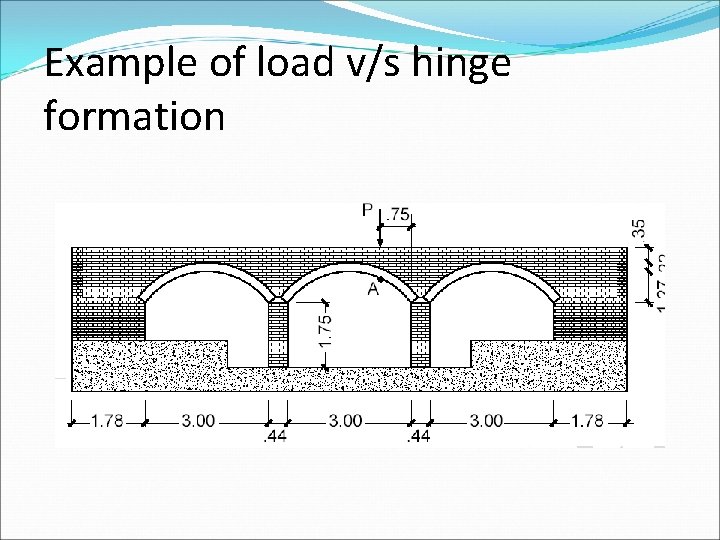
Example of load v/s hinge formation

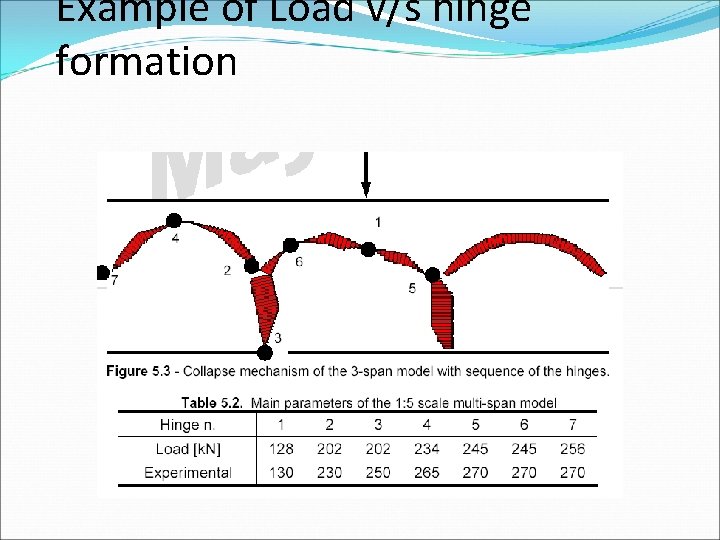
Example of Load v/s hinge formation

LOAD CARRYING CAPACITY ASSESSMENT

ARCH BRIDGE IS DIFFICULT? Least understood Not taught in academic institutions Inadequate coverage in codes and manuals of IR Interaction of arch barrel & fill; fill & spandrel/parapet is yet not fully understood Inadequate knowledge of construction details Non-availability of drawings

Construction details (not visible) Ring thickening Haunches and backing Internal spandrel walls Cross vaults and open spandrels Materials (adjoining bridges can help) Joints

Possible extent of backing

THICKNESS OF ARCH

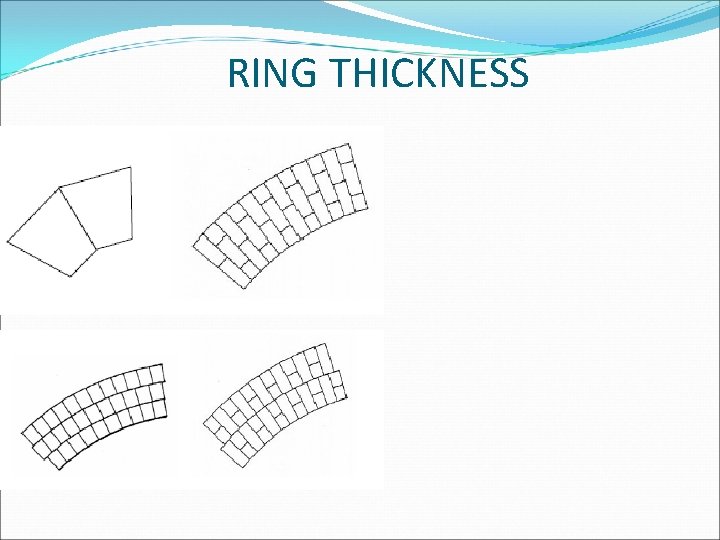
RING THICKNESS

STAGES IN ASSESSMENT Detailed field inspections of all the bridges. The requisite geometrical parameters obtained from field inspections. General condition of bridges recorded.

Assessment Methods MEXE METHOD MODIFIED MEXE METHOD RING ARCHIE – M Survey and tabulation method

MEXE METHOD First engineering method developed by Pippard & Ashby (1939) and Pippard (1948) for use in second world war. MEXE established in 1963 after full scale load tests carried out in 1950 s. Given in UIC code 778 -3 R. Empirical Method, no scope for parametric study.

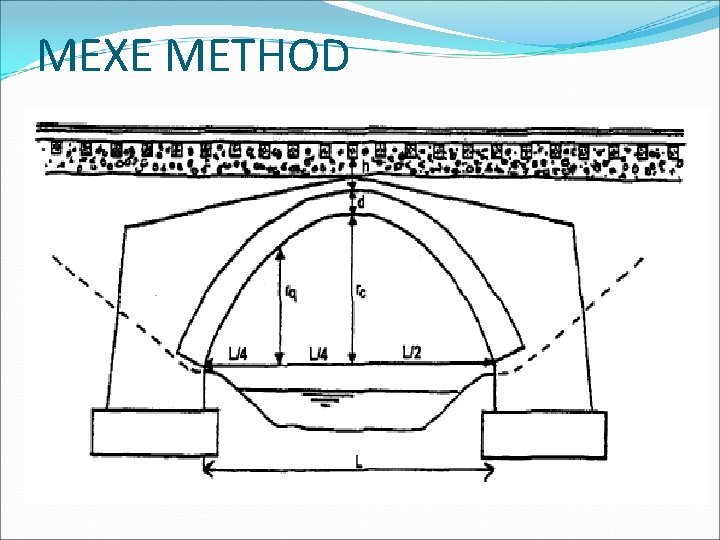
MEXE METHOD

MEXE METHOD Q = Qp. K Where K = Kp. Ks. Km. Kv. Kc Kp: profile factor Ks: Shape factor Km : material factor Kv : condition factor Kc : crack factor

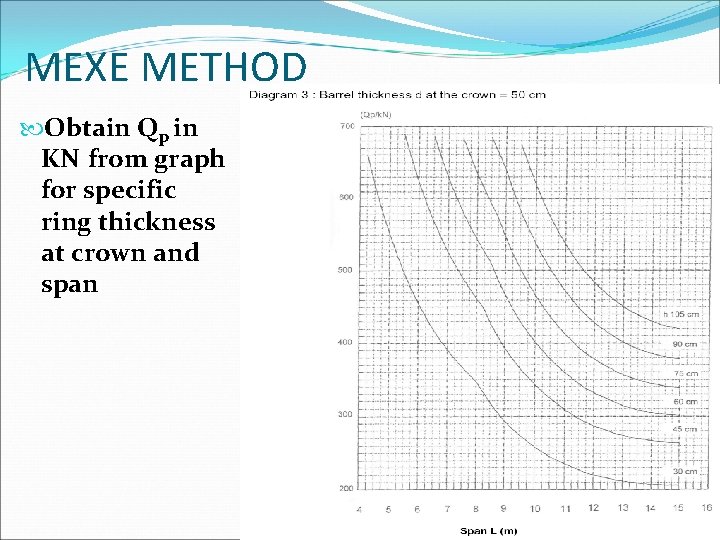
MEXE METHOD Obtain Qp in KN from graph for specific ring thickness at crown and span

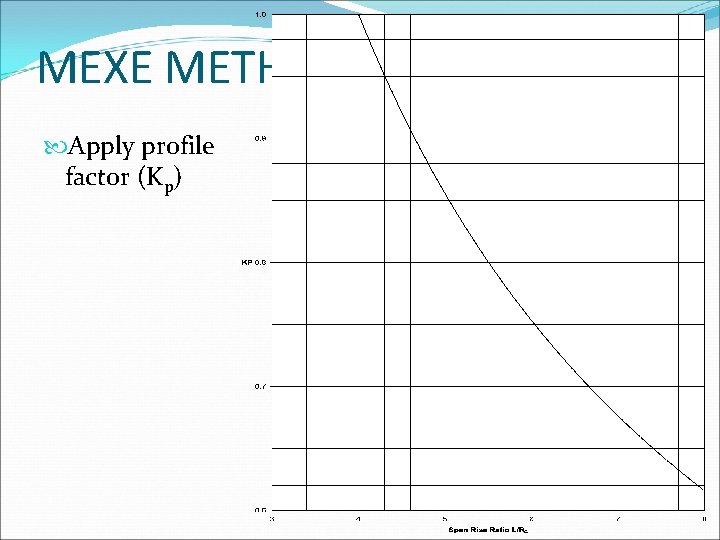
MEXE METHOD Apply profile factor (Kp)

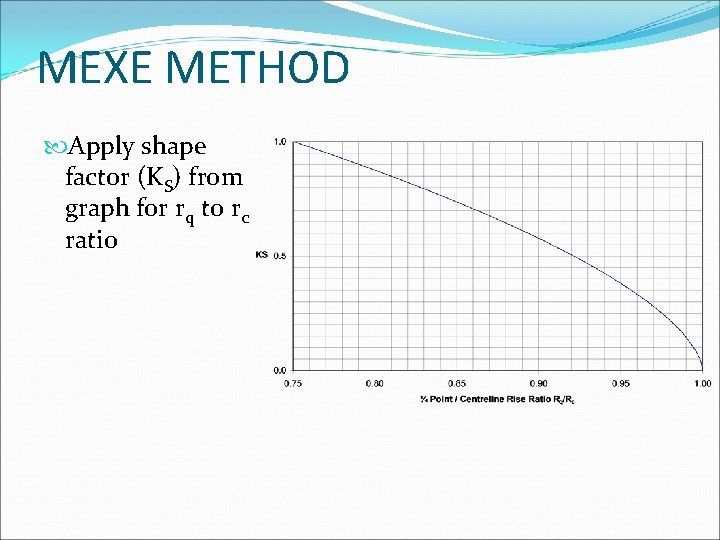
MEXE METHOD Apply shape factor (KS) from graph for rq to rc ratio

MEXE METHOD Material factor (KM) Soft brick and soft stone = 1. 0 Hard brick = 1. 2 Mass concrete = 1. 2 Stone Masonry = 1. 5

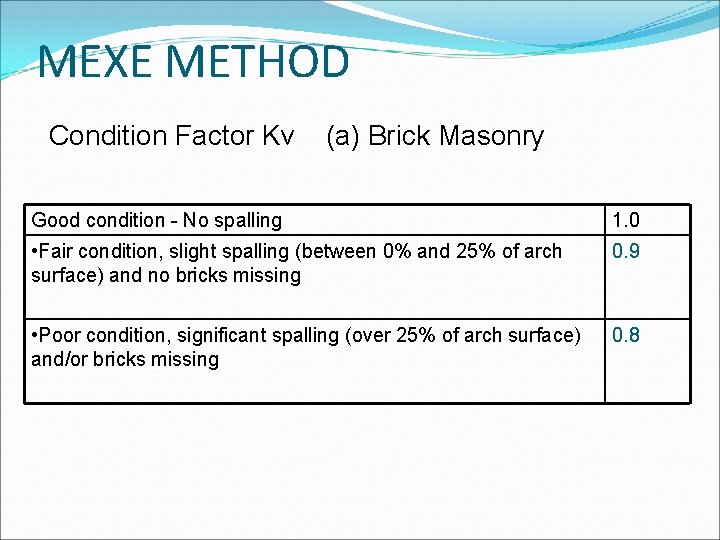
MEXE METHOD Condition Factor Kv (a) Brick Masonry Good condition - No spalling 1. 0 • Fair condition, slight spalling (between 0% and 25% of arch surface) and no bricks missing 0. 9 • Poor condition, significant spalling (over 25% of arch surface) and/or bricks missing 0. 8

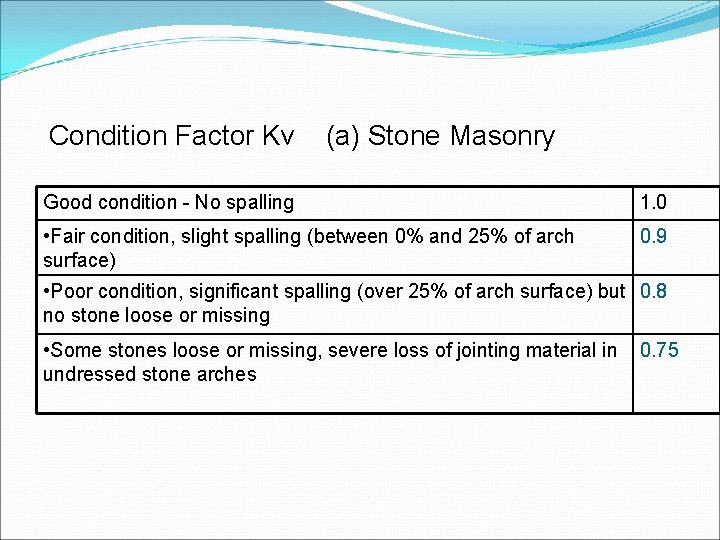
Condition Factor Kv (a) Stone Masonry Good condition - No spalling 1. 0 • Fair condition, slight spalling (between 0% and 25% of arch surface) 0. 9 • Poor condition, significant spalling (over 25% of arch surface) but 0. 8 no stone loose or missing • Some stones loose or missing, severe loss of jointing material in undressed stone arches 0. 75

MEXE METHOD Crack factor (Kc) a) No cracks -1. 0 b) Longitudinal cracks: Outside the centre third of the arch, less than one tenth of the span in length 0. 95 Outside the centre third of the arch, longer than one tenth of the span in length 0. 90 Within the centre third of the arch, less than one tenth of the span in length 0. 90 Within the centre third of the arch longer than one tenth of the span in length 0. 85 c) Lateral and diagonal cracks: Up to three small lateral or diagonal cracks less than 3 mm in width and less than one tenth of the arch width 0. 90 Numerous small cracks as above in the centre third of the arch 0. 60

MEXE METHOD Apply all factors to obtain value of idealized axle load Apply CDA

MODIFIED MEXE METHOD Similar to MEXE method Obtain PAL (provisional axle load) from monogram Apply modifying and condition factors

ADVANTAGES Simple, quick and in-expensive. Input parameters are based on visual inspection and there is no need for supplementary testing.

DISADVANTAGES Generally significantly underestimates the load carrying capacity of elliptical and flat arches. Non-conservative results when fill is high, i. e. greater than 105 cm. Not transparent leading assessors to make assumptions without considering real structural implications. Location of limiting condition not available

DISADVANTAGES Modifying factors highly subjective. Masonry strength not used Cannot be used for arches with significant damage.

RING SOFTWARE RING 1. 5 version, developed by sheffield university, UK RING 2. 0 version is developed as part of UIC project and full version likely to be available by Nov. 2007. Trial version is available at www. masonryarch. com

INPUT PARAMETERS OF RING 1. 5 GEOMETRY 1. 2. 3. 4. No. of Spans. Width of Bridge to be analyzed Fill Depth from Arch Crown LHS & RHS Abutments & Piers a) Height b) Width at top & bottom c) No. of Blocks (i. e. no. of brick/stone layers). 5. Spans (for each) a) Shape (i. e. elliptical or circular or user defined) b) Clear Span. c) Rise d) No. of Rings (i. e. no. of brick/stone layers in Arch)

INPUT PARAMETERS OF RING 1. 5 Width of the bridge to be analyzed is a very sensitive parameter. An 1: 1 dispersion in the transverse direction i. e. perpendicular to track has been assumed under the sleepers subject to the max. width of the arch barrel. All input parameters are self-evident

INPUT PARAMETERS OF RING 1. 5 MATERIAL PROPERTIES MASONRY 1. 2. 3. 4. Unit weight. Radial Friction. Tangential Friction. Crushing Strength BACKFILL 1. 2. 3. 4. Unit weight. Fill Friction. Dispersion Type. Horizontal Pressure.

INPUT PARAMETERS OF RING 1. 5 For arch bridges found sound on visual inspection, a crushing strength value of 10 N/mm 2 can be assumed. For arches with some sort of visual distress, a value of 5 N/mm 2 has been assumed. Default values of other parameters given and can be adopted. Classical horizontal pressure distribution with coefficient of earth pressure 0. 33 adopted with the option for automatic selection of passive pressure zones. Default values of solution convergence tolerance and max. no. of iterations have been adopted.

INPUT PARAMETERS OF RING 1. 5 LOADING Load vehicle can be created as per MBG or any other loading 2. Width of load is an important input parameter. This has been input as the length of sleeper as load will act on the fill of the arch through the sleepers 1.

EFFECT OF HAUNCHING/BACKING (mm) LOAD FACTOR NIL 600 1000 8. 910 16. 20 21. 40 Backing has significant effect on this particular arch, Load factor increases by more than double with backing of 1000 mm

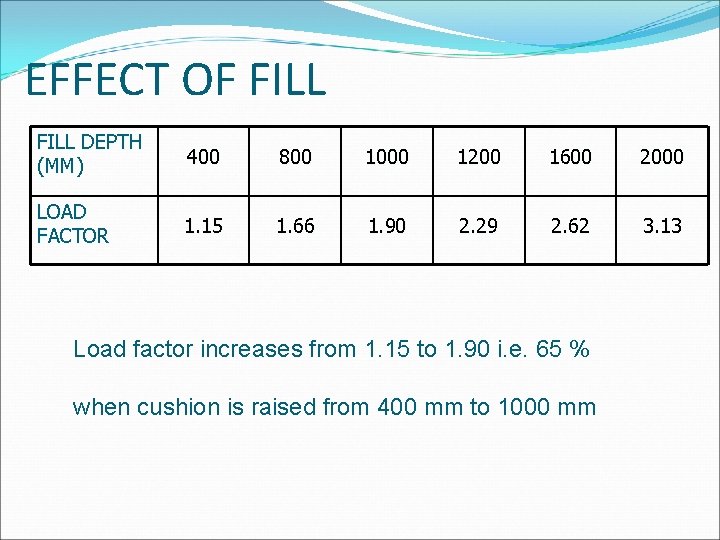
EFFECT OF FILL DEPTH (MM) 400 800 1000 1200 1600 2000 LOAD FACTOR 1. 15 1. 66 1. 90 2. 29 2. 62 3. 13 Load factor increases from 1. 15 to 1. 90 i. e. 65 % when cushion is raised from 400 mm to 1000 mm

EFFECT OF MASONRY STRENGTH N/mm 2 LOAD FACTOR 1 2 3 5 10 20 INFINI TE 1. 20 1. 53 1. 73 1. 90 2. 11 2. 24 2. 36 Bad looking masonry having crushing strength of 3 N/mm 2 have load factor only 16% lower than very good masonry of crushing strength of 10 N/mm 2. Interestingly, even if masonry strength is made infinite, increase in load factor is marginal.

CONCLUSIONS Fill increases LCC of masonry arches significantly Some minimum strength of arch material is required beyond which increase in strength of material affects LCC of masonry arches insignificantly Backing/ haunching in an arch bridge definitely increases LCC, extent of increase may be significant or insignificant depending upon arch configuration Arch is not a structure, which can be analyzed easily and accurately. Whenever strength of an arch is to be assessed, a through investigation of its special features and their effect on load carrying capacity needs to be studied. Arches in most cases will have much more strength than what is normally assumed

FINAL WORD ON ASSESSMENT • Inspection, past history and theoretical calculations (load test if reqd. ) are all inputs for taking final decision on estimated load carrying capacity of the arch bridge. Despite use of various assessment methods available, there is no substitute of engineering judgment and tendency to only follow results of theoretical calculations is wrong • Assessment of existing structures is job of an engineer, not of a designer

S K N T A H