Marwan K Abbadi Advisor Dr Winfred Anakwa Outline

Marwan K. Abbadi Advisor: Dr. Winfred Anakwa

Outline • Introduction – Problem definition – Objectives • • • Functional Description System Block Diagram System Identification Control Algorithm Software Implementation Hardware Interface Results Conclusions Future work

Introduction • What are Magnetic levitation systems? Maglev. are devices that suspend ferromagnetic materials with the aid of electromagnetism. It has wide number of applications such as high-speed trains, aerospace shuttles, magnetic bearings and high-precision platforms.

Introduction • Problem definition Maglev. systems based on electromagnetic attraction are characterized by non-linear and unstable open-loop dynamics which suggests the need of stabilizing controllers.

Project Objectives • Obtain a good model for the magnetic levitation system, maglev model 33 -210 from Feedback Inc. Limited. • Design and implement a microcontroller-based digital controller to stabilize a 21 gram steel ball at a desired vertical position. The overall system should track applied reference input signals.

Functional Description • Inputs: – Set point (Constant 1. 50 [V] ), corresponds to a distance of 22. 5 mm between the ball and the electromagnet. – Reference signal (± 0. 4 Vpp) – Disturbances such as power supply fluctuation, coil temperature variations and external forces applied to the ball. • Output Actual ball position

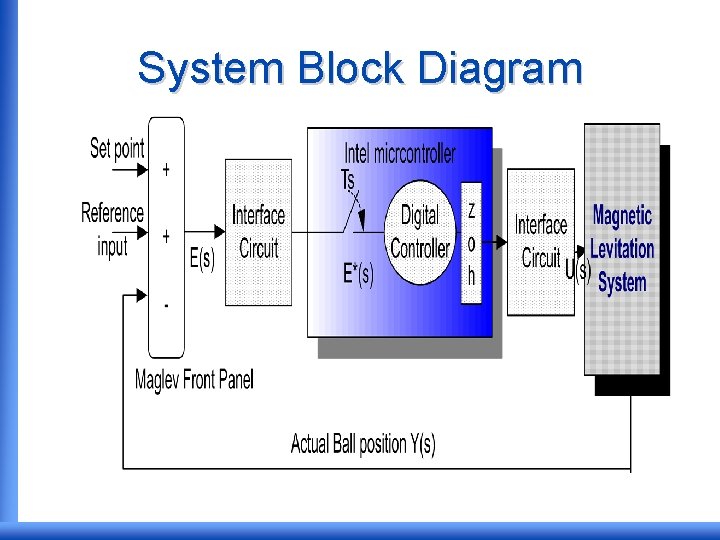
System Block Diagram

System Identification • Importance of modeling the system. • There are two approaches to identify the plant: a) Analytical model- Using differential equations. b) Experimental model- Bode frequency response data fitting. To obtain a good model for the system, both models were obtained for comparison.

System Identification • Analytical model There are two sets of equations that describe magnetic levitation systems. This is the general electrical 1) Electrical: circuit for magnetic levitation systems. However, this maglev. system is driven by an active circuit for the coil that adds further non-linearity since I is a non-linear function of e. Where e = Coil input voltage R= Coil resistance i = Coil current L= Coil inductance t = Time L 0= Nominal point inductance x 0= Nominal point pos.

System Identification 2) Mechanical equation Using Newton motion: 2 nd law of Electromagnetic force EF= C (i/x)2 Where F= Resultant force m= Mass of the steel ball= 0. 021 Kg g= gravitational acceleration = 9. 82 m/s 2 C= Magnetic plant constant Gravitation force GF = m*g

System Identification • The previous equation contained non-linear elements, so linearization is needed. • Taylor series expansion is used to approximate the equations near the operating point of x 0=22. 5 mm from electromagnet. • Operating region= 18 27 mm from electromagnet. • Magnetic plant constant, C= 1. 477 x 10 -4 N. m 2. A-2

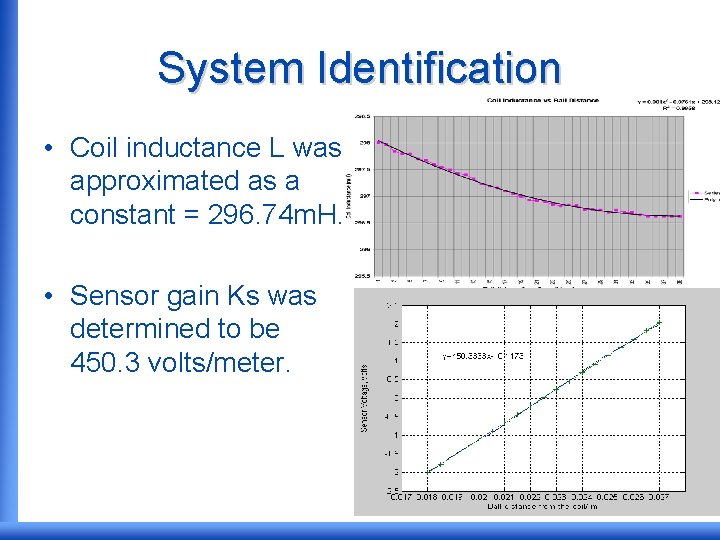
System Identification • Coil inductance L was approximated as a constant = 296. 74 m. H. • Sensor gain Ks was determined to be 450. 3 volts/meter.

System Identification • Combining the previous equations:

System Identification • The analog controller of the manufacturer was connected to the plant to obtain frequency response data. • The data was obtained at the nominal operating point x=x 0=22. 5 mm • The reference input frequency was swept from 0 to 20 Hz.

System Identification • The experimental model of the plant is:

System Identification • The experimental model was used instead of the analytical model, since the analytical model did not account for the non-linearity of the active coil driver. • The high-frequency pole at -70. 15 rad/s was omitted in the practical model approximation.

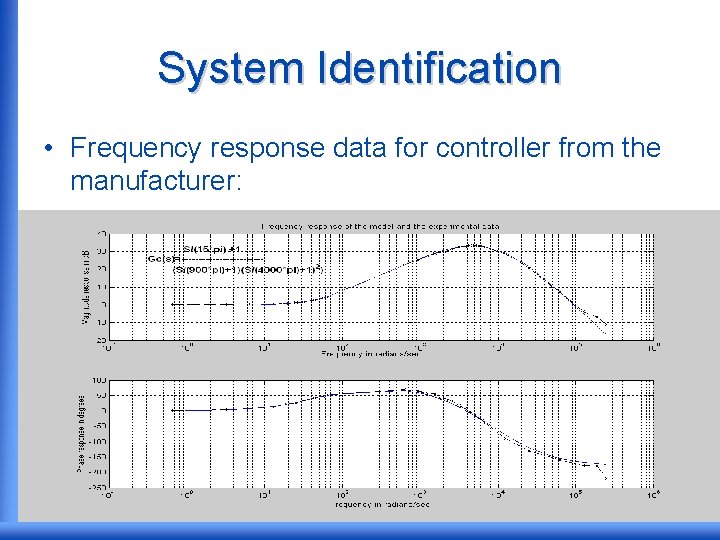
System Identification • Frequency response data for controller from the manufacturer:

System Identification • Controller from manufacturer: • Approximating to a first order: • Pole at -2827 rad/s and zero at -47 rad/s

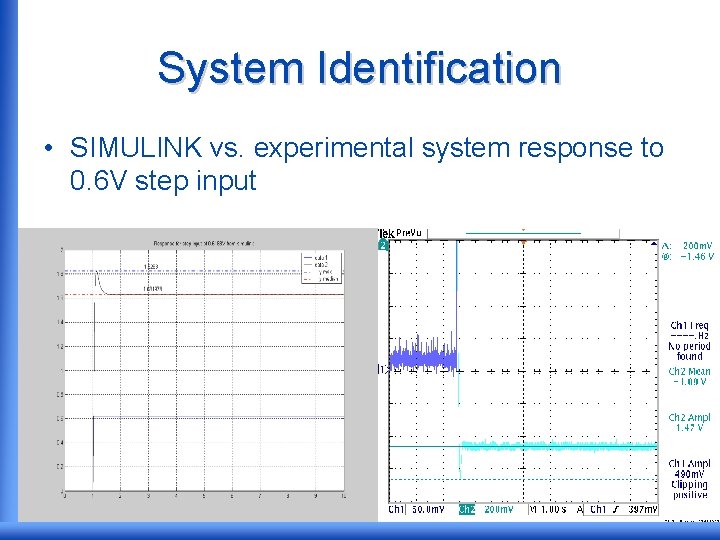
System Identification • SIMULINK vs. experimental system response to 0. 6 V step input

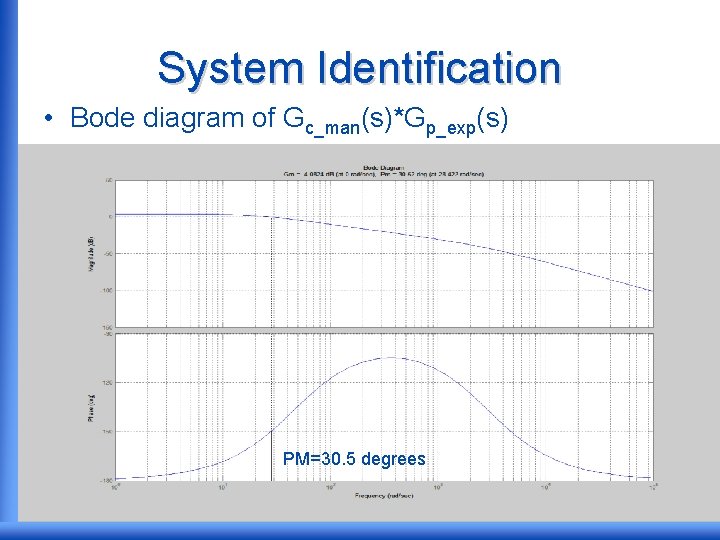
System Identification • Bode diagram of Gc_man(s)*Gp_exp(s) PM=30. 5 degrees

System Identification • The analog controller from manufacturer was converted to discrete domain using bilinear (Tustin) transformation with Ts= 5 ms.

Software Implementation • The digital controller was implemented using assembly language program on an Intel-80515 microcontroller. • The software code: – Samples the error signal via the A/D. – Computes the control signal. – Sends the control signal to the plant via the D/A.

Software Implementation • The 8051 microcontroller does not handle floating point arithmetic. • The controller transfer function was approximated for fixed point implementation. • The approximated transfer function: Note: Gain implemented in hardware

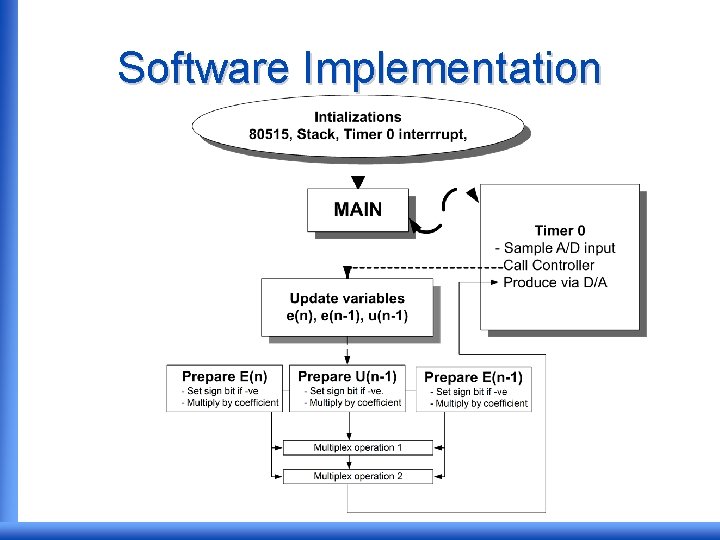
Software Implementation

Hardware Interface • Hardware interface circuitry is needed to level shift and scale the error to the range of the microcontroller A/D. • Furthermore, the control signal generated via the D/A must be readjusted back to the full scale and multiplied by the controller gain.

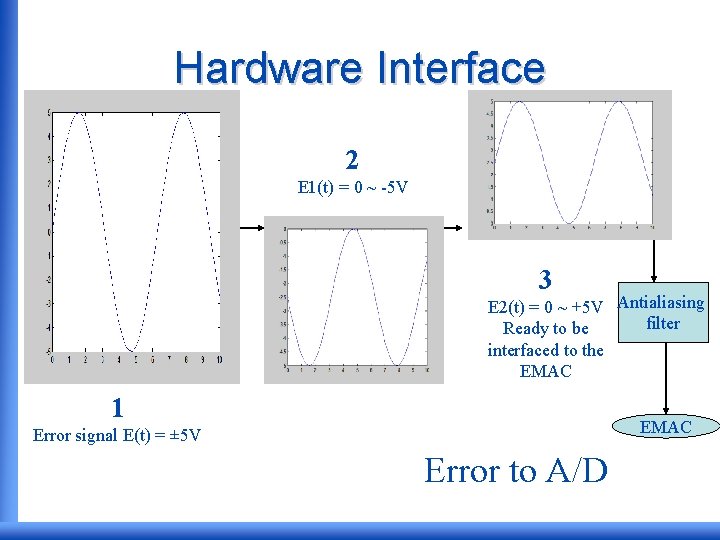
Hardware Interface 2 E 1(t) = 0 ~ -5 V 3 E 2(t) = 0 ~ +5 V Antialiasing filter Ready to be interfaced to the EMAC 1 EMAC Error signal E(t) = ± 5 V Error to A/D

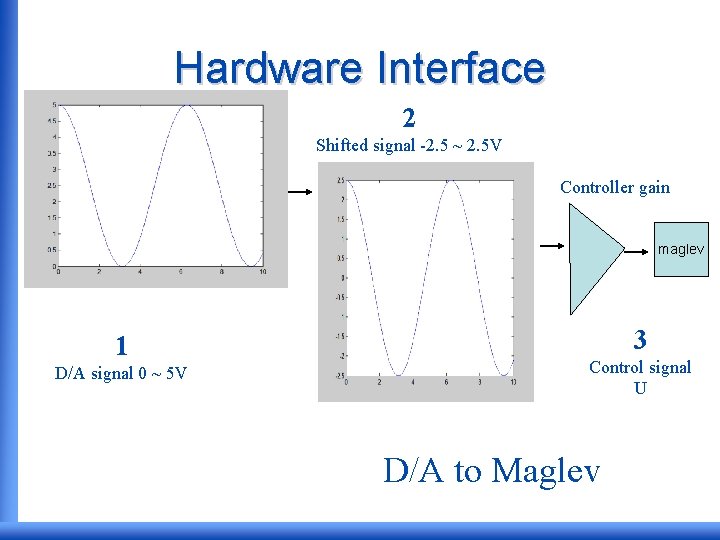
Hardware Interface 2 Shifted signal -2. 5 ~ 2. 5 V Controller gain maglev 1 D/A signal 0 ~ 5 V 3 Control signal U D/A to Maglev

Results • The ball was stabilized at the equilibrium point however it was oscillating due to: – Quantization errors of the 8 -bit A/D and D/A. – Truncation errors of coefficients stated in controller transfer function. – Computational truncation errors.

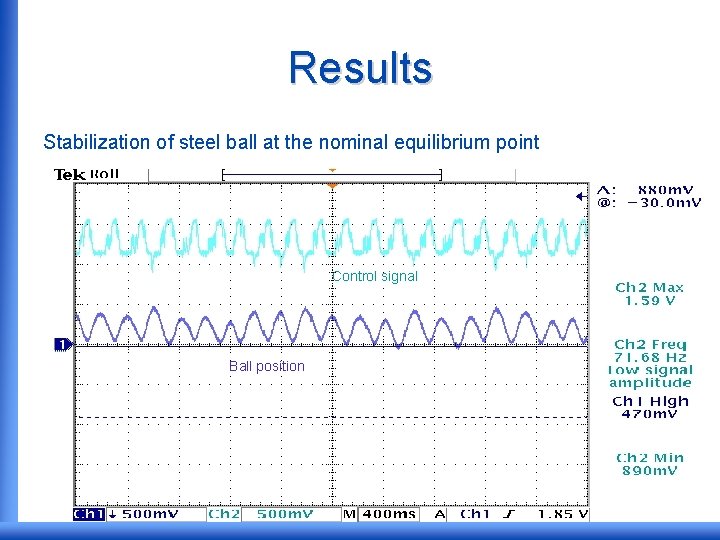
Results Stabilization of steel ball at the nominal equilibrium point Control signal Ball position

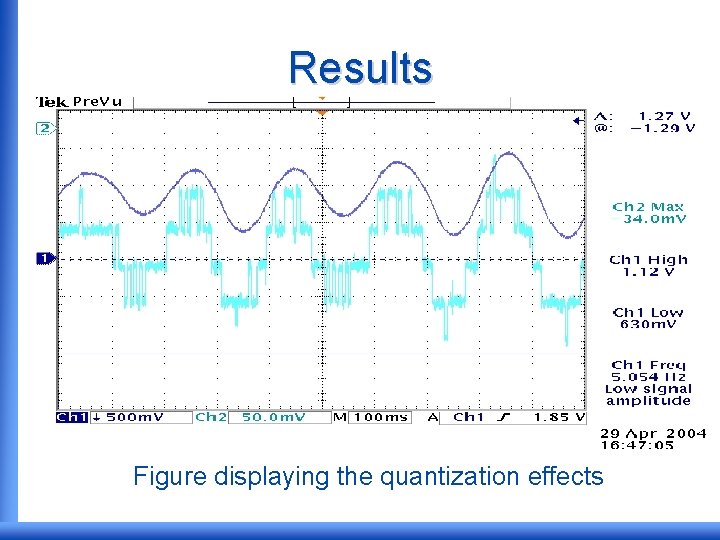
Results Figure displaying the quantization effects

Results

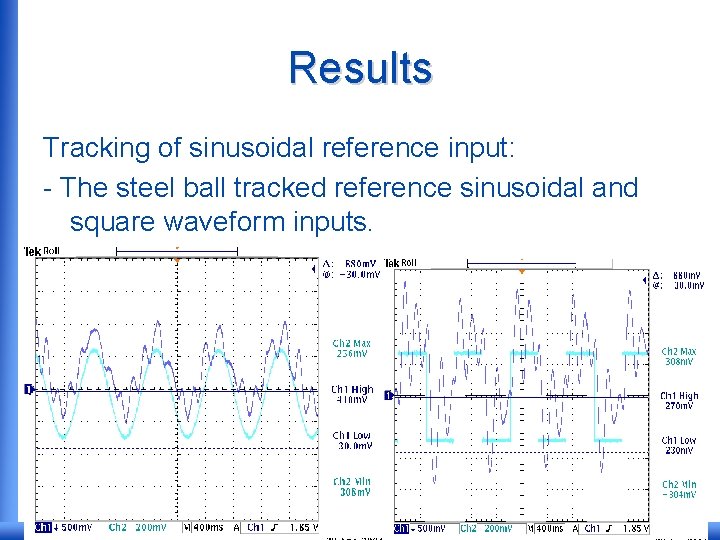
Results Tracking of sinusoidal reference input: - The steel ball tracked reference sinusoidal and square waveform inputs.

Conclusions • Mathematical modeling of an unstable system is a challenging control engineering problem. Some examples are inverted pendulums and aerospace vehicles. • Implementation of controller algorithm on 8 -bit microcontroller using fixed point arithmetic generates quantization and truncation errors. • These errors, that depend on sampling period and controller gain, cause small oscillations in system response. • The ball tracked reference input signals. Better tracking performance can be achieved using higher resolution A/D and D/A, longer wordlength microcontroller and a higher order controller.

Future work • A user-friendly interface can be developed using the keypad and LCD. • Possible user inputs include sampling period, poles and zeroes locations, settling time etc. • Once implemented, the system will serve as a good apparatus for teaching undergraduate controls students the effect of varying different parameters on overall system response.

END Questions and answers Thank you For more information: visit http: //cegt 201. bradley. edu/projects/proj 2003/maglev/