Markov Models Markov Models Markov Models can be

Markov Models

Markov Models • Markov Models can be seen as special cases of finite state automata • Specifically, weighted finite state automata • Very simply, one can imagine a markov model as being a FSA decorated with probabilities • (There’s more to it than that, but this is sufficient for now. )

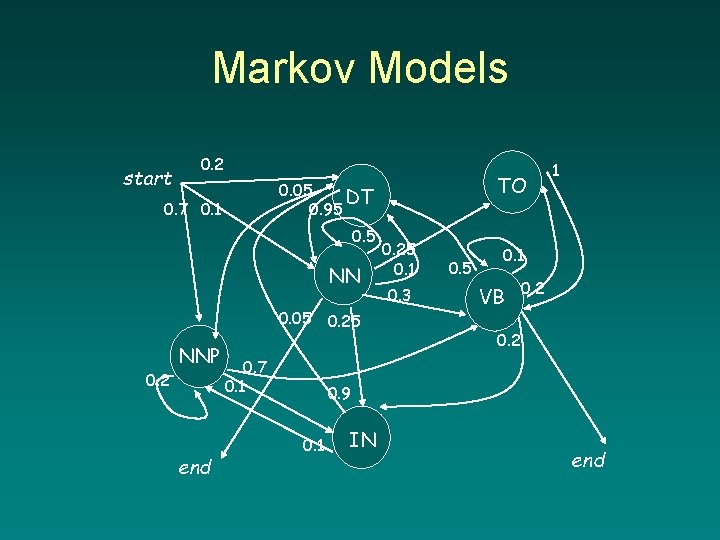
Markov Models start 0. 2 0. 7 0. 1 0. 5 NN 0. 05 0. 2 NNP end TO 0. 05 DT 0. 95 0. 7 0. 1 0. 25 0. 1 0. 3 0. 5 1 0. 1 VB 0. 2 0. 9 0. 1 IN end

Markov Models • A Markov Model consists of the following: – A finite set of states S = {1, 2, …, n}. – A set of transition probabilities between states P = {p 11, p 12, …, pnn}. – For each transition probability pij P, pij 0. – And the following property holds: pij = 1 j S

Markov Models • The set of transition probabilities can be arranged in a matrix: A= [ p 11 p 12 …p 1 j p 21 p 22 …p 2 j … ] • Sang also describes a matrix Π, which is the set of probabilities for each starting state

Markov Model • Formally, then, a Markov Model is a 3 tuple (S, Π, A). • For NLP applications, how are the probabilities derived? – Can be hand-coded – Usually derived from data, often a corpus

Markov Models and NLP • Exercise – Build the transition probability matrix and over this set of data The duck died. The car killed the duck. The duck died under her car. We duck under the car. We retrieve the poor duck. – Build the starting probability matrix

Markov Models and NLP • Exercise – What’s the probability for some given output? The duck died under her car. We duck under the car. The duck under the car. We retrieve killed the duck. We the poor duck died. We retrieve the poor duck under the car. – For a given start state (The, We), what’s the most likely string to be output?

Markov Models • The homework