Markov Models CS 6800 Advanced Theory of Computation

Markov Models CS 6800 Advanced Theory of Computation Fall 2012 Vinay B Gavirangaswamy

Markov Property Processes future values are conditionally dependent on the present state of the system. Strong Markov Property Similar as Markov Property, where values are conditionally dependent on the stopping time (Markov time) instead of present state. Introduction

Markov Process that follows Markov Property. e. g. First order Markov Process for probability space ( , F, P) P(Xt+1=Sj | Xt=Si, Xt-1=Sk , . . . ) = P(Xt+1=Sj | qt=Si) , for t = 1, 2, 3, … where, = {S 1, S 2, S 3, …, Sn }, State at time t is Xt=Si Markov Model’s a stochastic system which assumes Markov property. It is formally represented by triplet M = (K, , A), where K is a finite set of states vector of initial probabilities for each of the states. A is a matrix representing transition probabilities. Markov model is an non deterministic finite state machine. Introduction (Contd. )

Stochastic FSM The transition matrix: • Stochastic matrix: Rows sum up to 1 • Double stochastic matrix: Rows and columns sum up to 1 Simple Markov Model of Weather

� If we want to know probability of the sequence SUNNY SUNNY � Take initial probability of SUNNY day i. e. on a any given day probability that it will be SUNNY is 0. 30 � And for use to get another SUNNY day after a SUNNY day is 0. 42 � So, by using Markov Chain we can say probability of getting 5 consecutive SUNNY day is Prediction Based on State Transition Probability

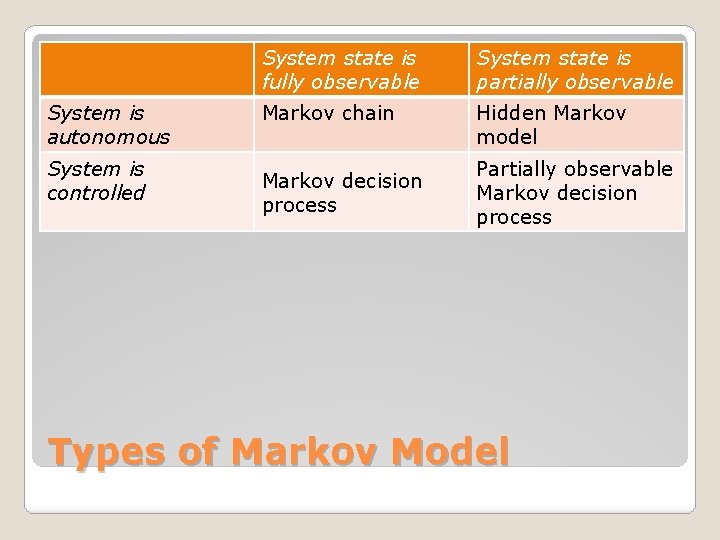
System is autonomous System is controlled System state is fully observable System state is partially observable Markov chain Hidden Markov model Markov decision process Partially observable Markov decision process Types of Markov Model

Markov Chain � Simplest Markov model � System state at time t+1 depends on state at t. Hidden Markov Model � Similar to Markov chain but system states are unobservable. Markov decision process � Models a system where outcomes are partially random and partially under the control of a decision maker. Types of Markov Model (Contd. )

Markov decision process It is formally represented by 4 -tuple M = (K, , A, R), where K is a finite set of states vector of initial probabilities for each of the states. A is a matrix representing transition probabilities. R is reward given for transition from state St to Sp with transition probability given in matrix A. Types of Markov Model (Contd. )

Partially observable Markov decision process Similar to Markov decision process where state of system is partially observed. It is formally represented by 4 -tuple M = (K, , O , A, ), where K is a finite set of states. is a set of actions. O is a set of observations. A is a matrix representing transition probabilities. is a set of conditional observation probabilities. Types of Markov Model (Contd. )

� System that transitions from one state to another, between a finite number of possible states. � Next state depends only on current state and not its history. � Follows Markov property. � Formally for a stochastic process { Xt } P{ Xt+1 = j | X 0 = k 0, . . . , Xt-1 = kt-1, Xt = i } = P{ Xt+1 = j | Xt = i } for every � i, j, k 0, . . . , kt-1 and for every t. Stationary Markov Chains Pr{ Xt+1 = j | Xt = i } = Pr{ X 1 = j | X 0 = i } for all t Markov Chain

�If the state space S = { 0, 1, . . . , m– 1} then we have j pij = 1 i and pij 0 i, j (we must go some where) (each transition has probability 0) where pij = Pr{ X 1 = j | X 0 = i } Transition Matrix 11

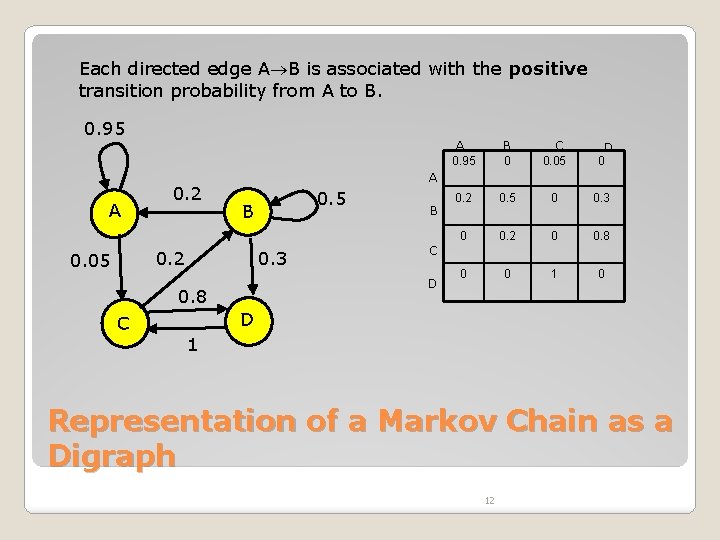
Each directed edge A B is associated with the positive transition probability from A to B. 0. 95 A 0. 2 0. 5 B 0. 3 B C 0. 05 0. 2 0. 5 0 0. 3 0 0. 2 0 0. 8 0 0 1 0 D 0 C D 0. 8 C B 0 A 0. 2 0. 05 A 0. 95 D 1 Representation of a Markov Chain as a Digraph 12

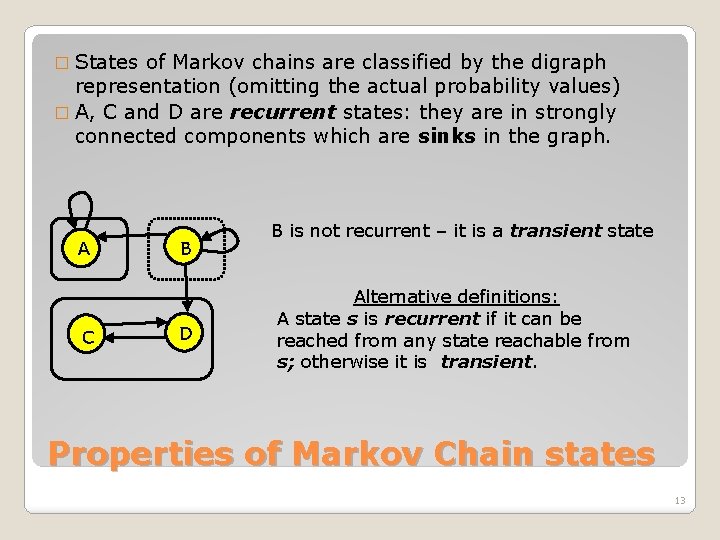
� States of Markov chains are classified by the digraph representation (omitting the actual probability values) � A, C and D are recurrent states: they are in strongly connected components which are sinks in the graph. A C B D B is not recurrent – it is a transient state Alternative definitions: A state s is recurrent if it can be reached from any state reachable from s; otherwise it is transient. Properties of Markov Chain states 13

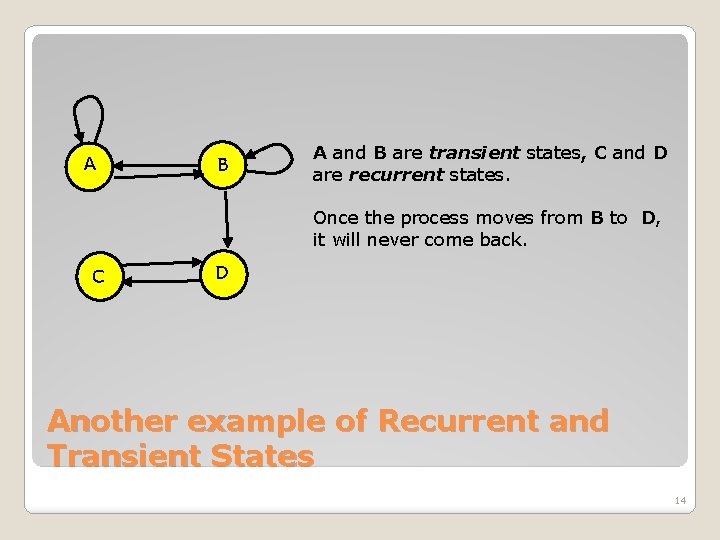
A B A and B are transient states, C and D are recurrent states. Once the process moves from B to D, it will never come back. C D Another example of Recurrent and Transient States 14

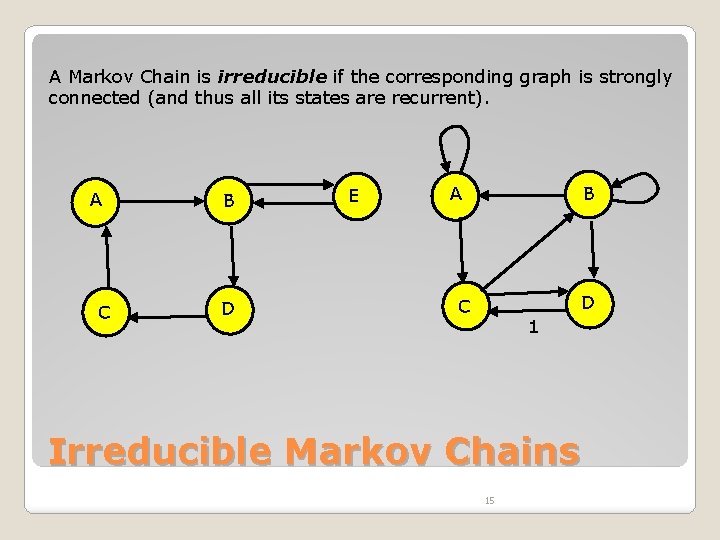
A Markov Chain is irreducible if the corresponding graph is strongly connected (and thus all its states are recurrent). A C B D E A B D C 1 Irreducible Markov Chains 15

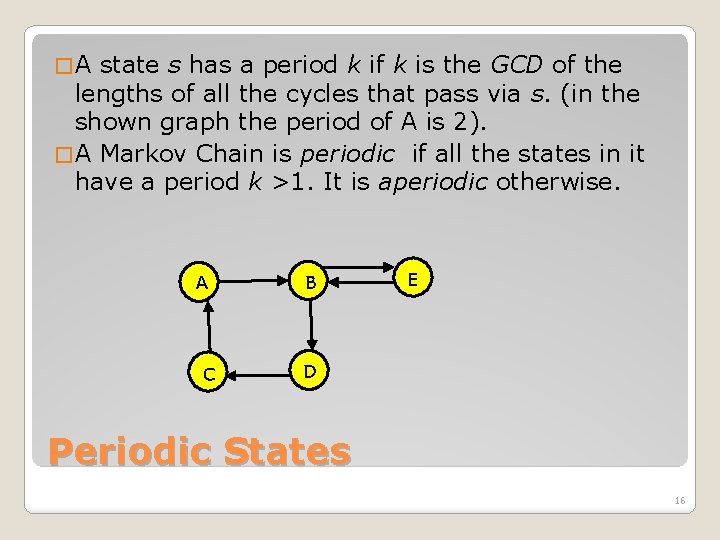
�A state s has a period k if k is the GCD of the lengths of all the cycles that pass via s. (in the shown graph the period of A is 2). � A Markov Chain is periodic if all the states in it have a period k >1. It is aperiodic otherwise. A C B E D Periodic States 16

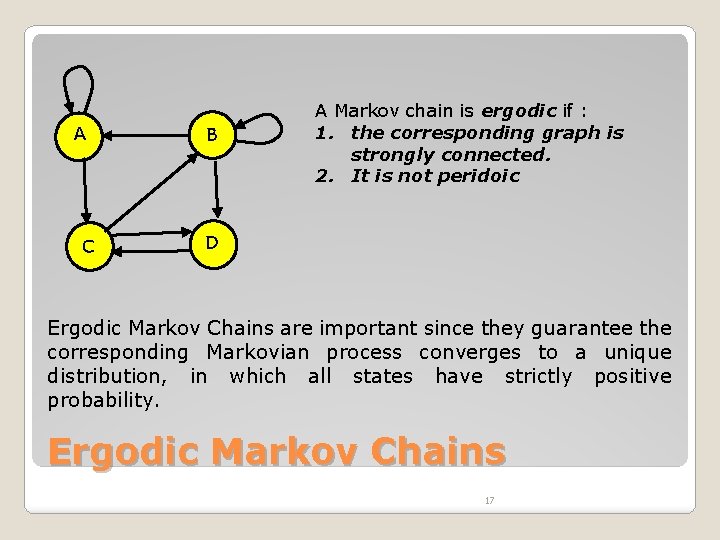
A C B A Markov chain is ergodic if : 1. the corresponding graph is strongly connected. 2. It is not peridoic D Ergodic Markov Chains are important since they guarantee the corresponding Markovian process converges to a unique distribution, in which all states have strictly positive probability. Ergodic Markov Chains 17

A Markov chain is reversible if Reversible Markov chain

� Physics � Chemistry � Testing � Information sciences � Queuing theory � Internet applications � Statistics � Economics and finance � Social science � Mathematical biology � Games � Music Markov Model Applications

� "Wkipedia-Markov model, " [Online]. Available: http: //en. wikipedia. org/wiki/Markov_chain. [Accessed 28 10 2012]. � P. Xinhui Zhang, "DTMarkovchains, " [Online]. Available: http: //www. wright. edu/~xinhui. zhang/. [Accessed 28 10 2012]. References