Markov Models Agenda Homework Markov models Overview Some

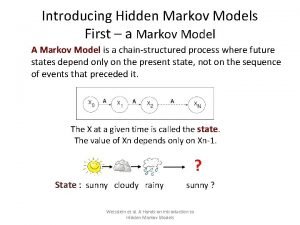
Markov Models

Agenda • Homework • Markov models – Overview – Some analytic predictions – Probability matching • Stochastic vs. Deterministic Models • Gray, 2002

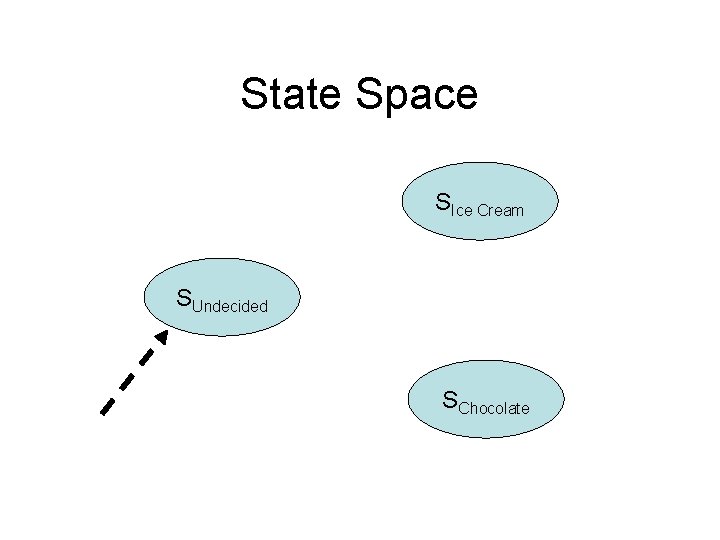
Choice Example • A person is given a choice between ice cream and chocolate. • The person can be – Undecided. – Choose ice cream. – Choose chocolate. • There is some probability of going from being undecided to – Staying undecided and giving no decision. – Choosing ice cream. – Choosing chocolate.

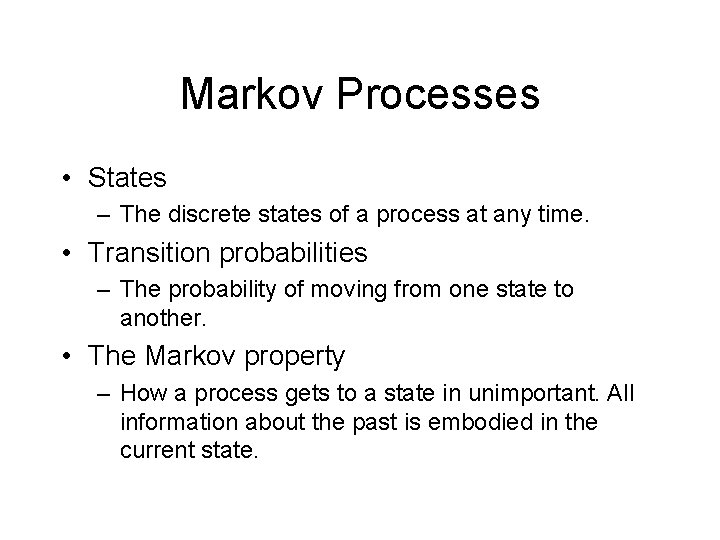
Markov Processes • States – The discrete states of a process at any time. • Transition probabilities – The probability of moving from one state to another. • The Markov property – How a process gets to a state in unimportant. All information about the past is embodied in the current state.

State Space SIce Cream SUndecided SChocolate

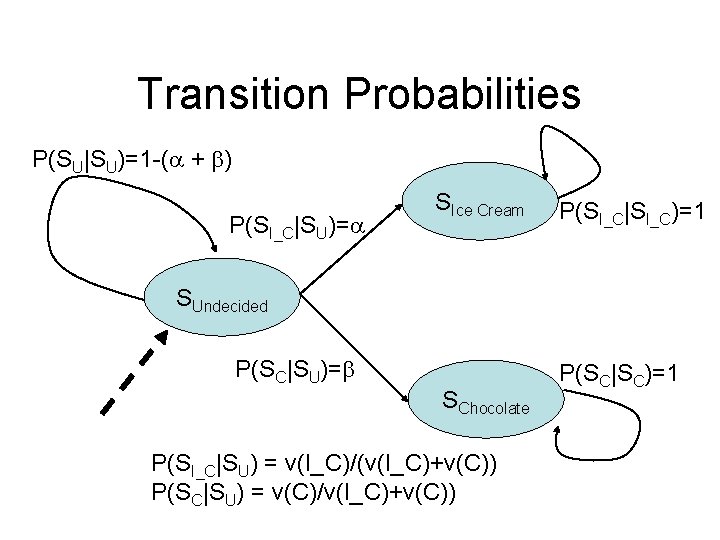
Transition Probabilities P(SU|SU)=1 -( + ) P(SI_C|SU)= SIce Cream P(SI_C|SI_C)=1 SUndecided P(SC|SU)= SChocolate P(SC|SC)=1 Note: The transition probabilities out of a node sum to 1. How can this model be made equivalent to Luce Choice?

Transition Probabilities P(SU|SU)=1 -( + ) P(SI_C|SU)= SIce Cream P(SI_C|SI_C)=1 SUndecided P(SC|SU)= SChocolate P(SI_C|SU) = v(I_C)/(v(I_C)+v(C)) P(SC|SU) = v(C)/v(I_C)+v(C)) P(SC|SC)=1

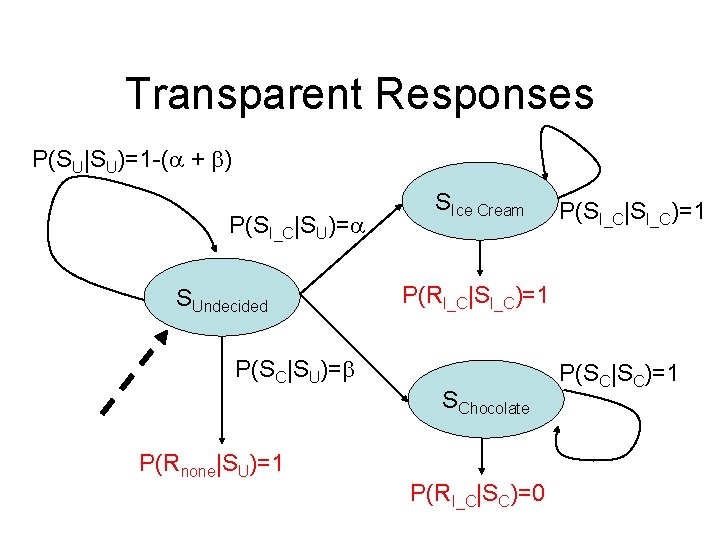
Transparent Responses P(SU|SU)=1 -( + ) P(SI_C|SU)= SUndecided SIce Cream P(RI_C|SI_C)=1 P(SC|SU)= SChocolate P(Rnone|SU)=1 P(SI_C|SI_C)=1 P(RI_C|SC)=0 P(SC|SC)=1

Transparent Responses P(SU|SU)=1 -( + ) P(SI_C|SU)= SUndecided SIce Cream P(RI_C|SI_C)=. 8 P(SC|SU)= SChocolate P(Rnone|SU)=1 P(SI_C|SI_C)=1 P(RI_C|SC)=. 2 P(SC|SC)=1

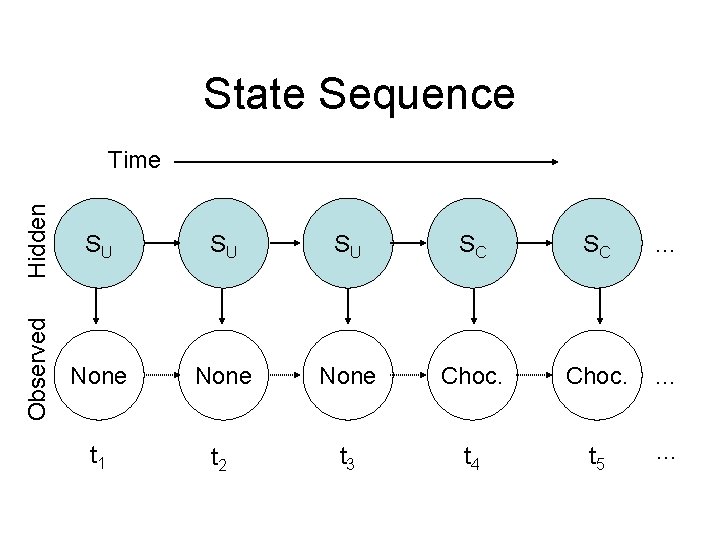
State Sequence Hidden SU SU SU SC SC … Observed Time None Choc. … t 1 t 2 t 3 t 4 t 5 …

Matrix Form of Transition Probabilities To From SU SI_C SC SU 1 -( + ) SI_C 0 1 0 SC 0 0 1

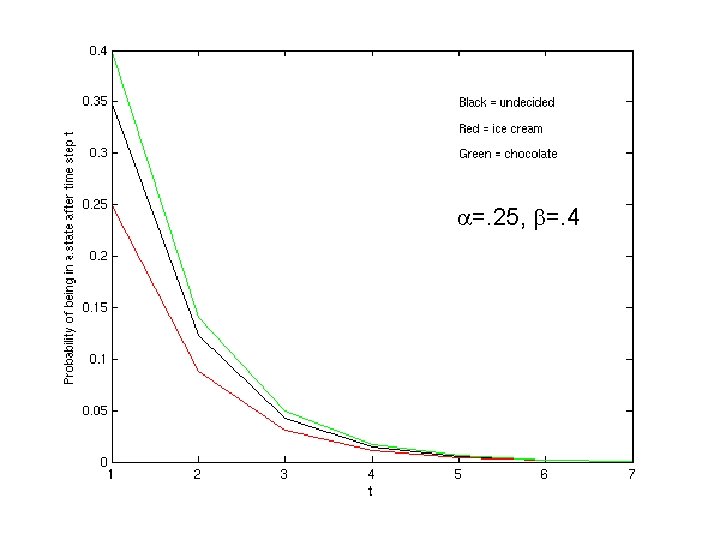
Some Analytic Solutions Where =P(SI_C|SU) and =P(SC|SU)

Some Analytic Solutions What happens if: • + =1? • t=1?

More Analytic Solutions

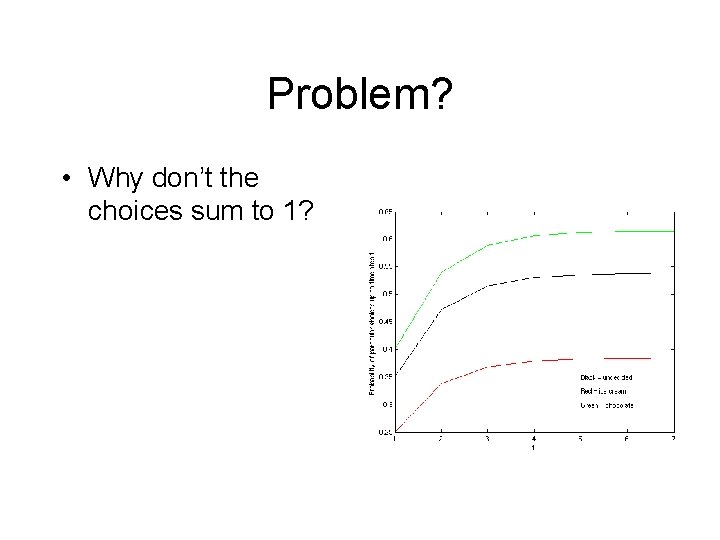
Problem? • Why don’t the choices sum to 1?

More Results… • The matrix form is very convenient for calculations. • It is easy to calculate all moments. • More to come with random walks…

Pair Clustering • Batchelder & Riefer, 1980 – Free recall of clusterable pairs. – Implements a Markov model for the probability that a pair is clustered on a particular trial. • Are MPTs Markov models?

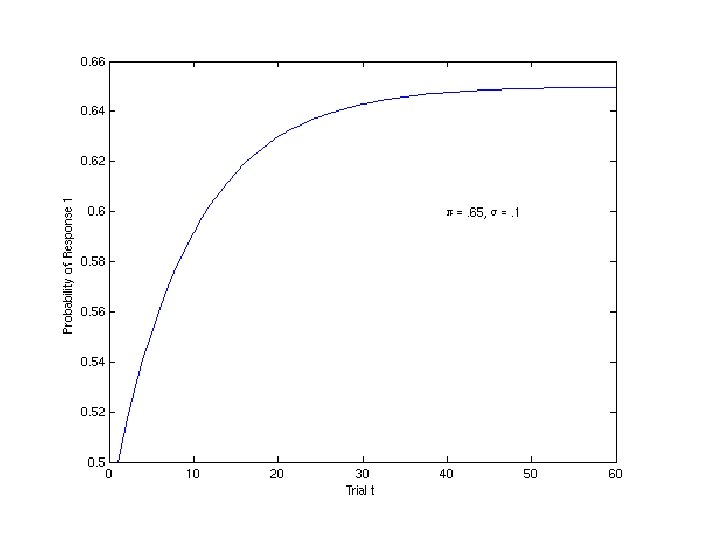
Probability Matching • Paradigm – Warning light – Prediction: P(R 1), P(R 2) – Feedback: P(E 1)= , P(E 2)=1 - • Typical result – P(R 1)

Probability Matching • Can be implemented via a Markov model. • Assume win-stay/lose-shift paradigm – If “correct”, make same prediction – If “incorrect”, shift response with probability . • Associate an “element” with most recent event, but not perfectly.

Current Trial Next Trial R 1 E 1 R 2 E 1 R 1 E 2 R 2 E 2 R 1 E 1 0 1 - 0 R 2 E 1 (1 - ) R 1 E 2 (1 - ) R 2 E 2 0 0 1 - Ri. Ej = Response i and then Feedback j. = Probability of Feedback 1. = Probability of switching after error.

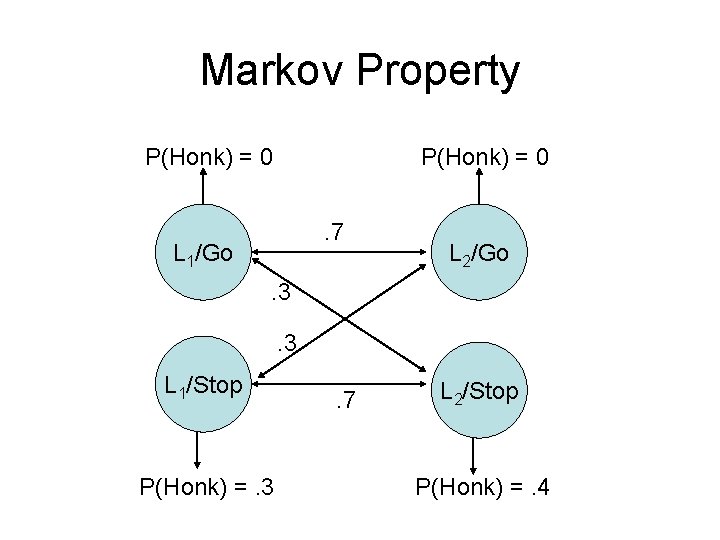
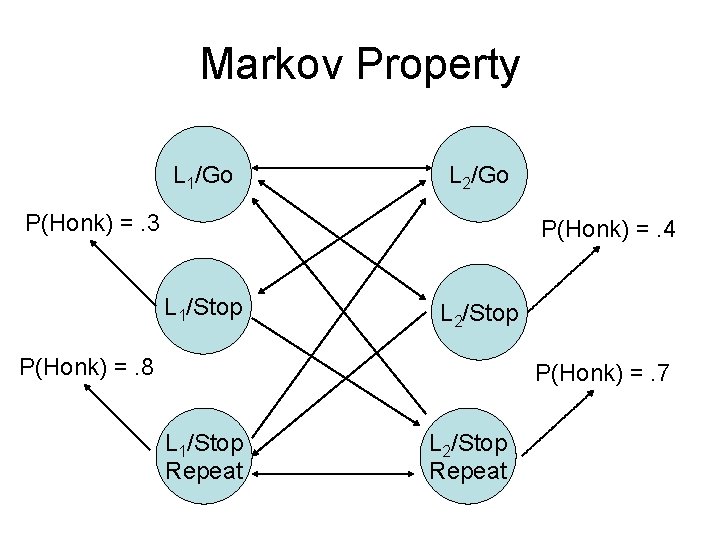
Markov Property

Light 2 Light 1

Markov Property P(Honk) = 0. 7 L 1/Go L 2/Go . 3. 3 L 1/Stop P(Honk) =. 3 . 7 L 2/Stop P(Honk) =. 4

Markov Property L 1/Go L 2/Go P(Honk) =. 3 P(Honk) =. 4 L 1/Stop L 2/Stop P(Honk) =. 8 P(Honk) =. 7 L 1/Stop Repeat L 2/Stop Repeat

Stochastic vs. Deterministic • Stochastic model: The processes are probabilistic. • Deterministic: The processes are completely determined.

Stochastic Models Imply: • Psychological events are uncertain – Even if we had all the knowledge we needed we could still not figure out what a person is going to do next. • Or

Stochastic Models Imply: • The model does not capture all aspects of the behavior in question – Allows the model to focus on certain parts of behavior and ignore others. – You may believe behavior is deterministic, but still rely on a stochastic model. – Allows the modeler to finesse some ignorance. • OR

Stochastic Models Imply: • Some parts of the task are truly random – E. g. , feedback schedule from the experimenter in a probability matching task.

Limitation of Stochastic Models • You need to test them on populations of behavior, not individual behaviors. – E. g. , I gave Participant X a single choice and she chose ice cream. – Can we test the model against this datum?