Markov Logic Overview Introduction Statistical Relational Learning Applications

Markov Logic

Overview • Introduction – Statistical Relational Learning – Applications – First-Order Logic • Markov Networks – – – What is it? Potential Functions Log-Linear Model Markov Networks vs. Bayes Networks Computing Probabilities

Overview • Markov Logic – – – – Intuition Definition Example Markov Logic Networks MAP Inference Computing Probabilities Optimization

Introduction

Statistical Relational Learning Goals: • Combine (subsets of) logic and probability into a single language • Develop efficient inference algorithms • Develop efficient learning algorithms • Apply to real-world problems L. Getoor & B. Taskar (eds. ), Introduction to Statistical Relational Learning, MIT Press, 2007.

Applications • Professor Kautz’s GPS tracking project – Determine people’s activities and thoughts about activities based on their own actions as well as their interactions with the world around them

Applications • Collective classification – Determine labels for a set of objects (such as Web pages) based on their attributes as well as their relations to one another • Social network analysis and link prediction – Predict relations between people based on attributes, attributes based on relations, cluster entities based on relations, etc. (smoker example) • Entity resolution – Determine which observations imply real-world objects (Deduplicating a database) • etc.

First-Order Logic • Constants, variables, functions, predicates E. g. : Anna, x, Mother. Of(x), Friends(x, y) • Literal: Predicate or its negation • Clause: Disjunction of literals • Grounding: Replace all variables by constants E. g. : Friends (Anna, Bob) • World (model, interpretation): Assignment of truth values to all ground predicates

Markov Networks

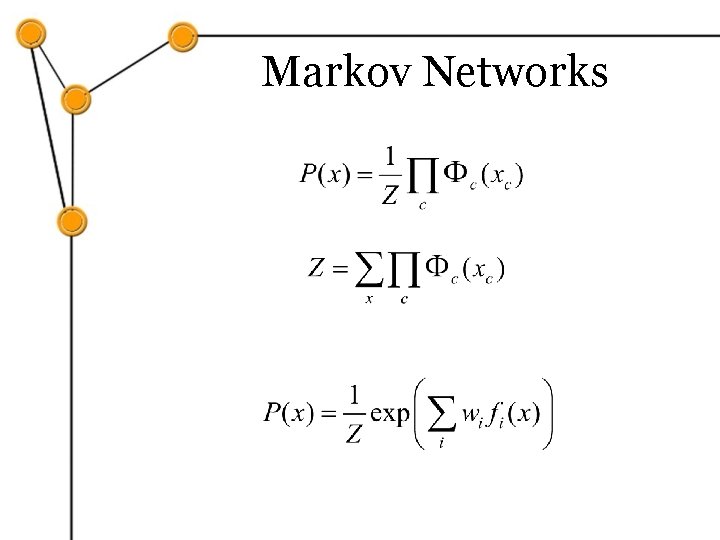
What is a Markov Network? • Represents a joint distribution of variables X • Undirected graph • Nodes = variables • Clique = potential function (weight)

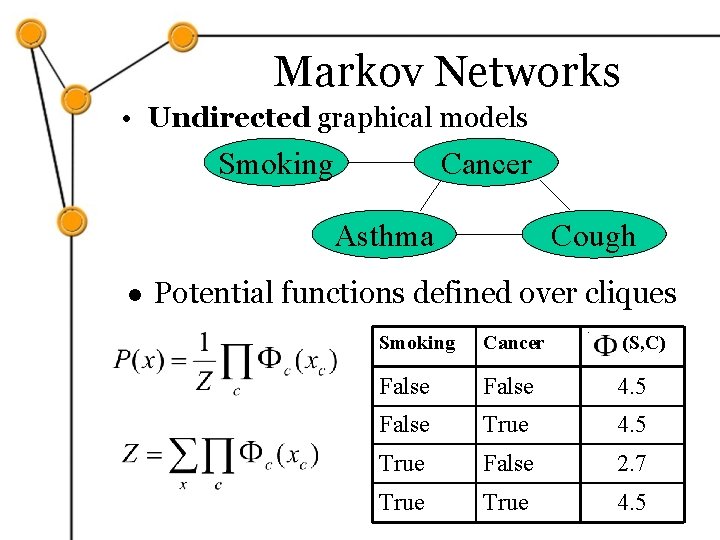
Markov Networks • Undirected graphical models Smoking Cancer Asthma l Cough Potential functions defined over cliques Smoking Cancer (S, C) False 4. 5 False True 4. 5 True False 2. 7 True 4. 5

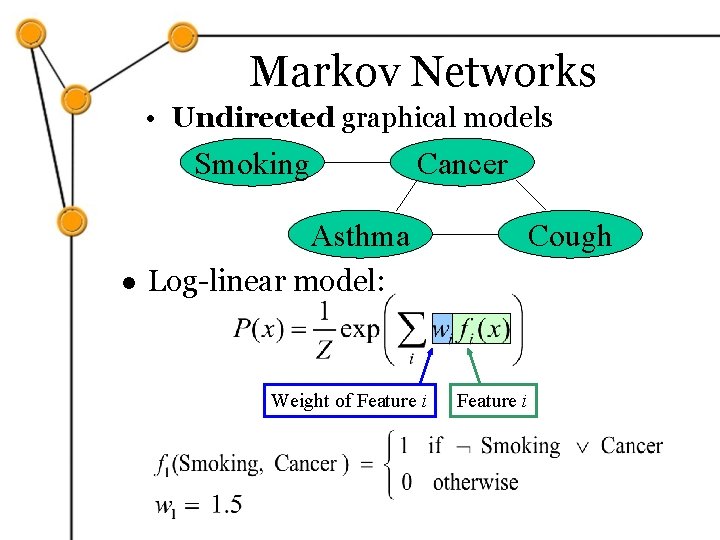
Markov Networks • Undirected graphical models Smoking Cancer Asthma l Cough Log-linear model: Weight of Feature i

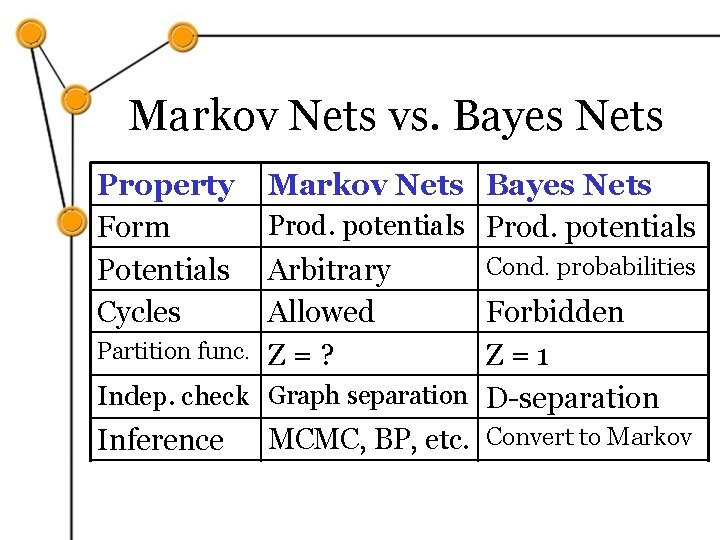
Markov Nets vs. Bayes Nets Property Form Potentials Cycles Markov Nets Bayes Nets Prod. potentials Cond. probabilities Arbitrary Allowed Forbidden Partition func. Z = ? Z=1 Indep. check Graph separation D-separation Inference MCMC, BP, etc. Convert to Markov

Computing Probabilities • Goal: Compute marginals & conditionals of • Exact inference is #P-complete • Approximate inference – Monte Carlo methods – Belief propagation – Variational approximations

Markov Logic

Markov Logic: Intuition • A logical KB is a set of hard constraints on the set of possible worlds • Let’s make them soft constraints: When a world violates a formula, It becomes less probable, not impossible • Give each formula a weight (Higher weight Stronger constraint)

Markov Logic: Definition • A Markov Logic Network (MLN) is a set of pairs (F, w) where – F is a formula in first-order logic – w is a real number • Together with a set of constants, it defines a Markov network with – One node for each grounding of each predicate in the MLN – One feature for each grounding of each formula F in the MLN, with the corresponding weight w

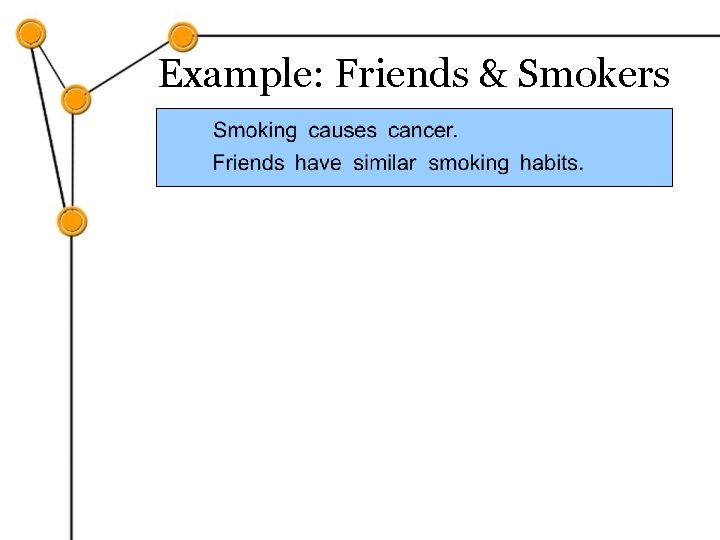
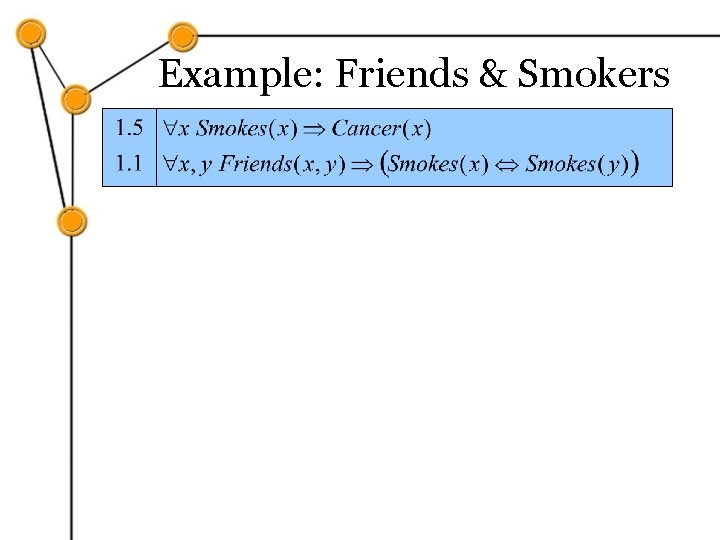
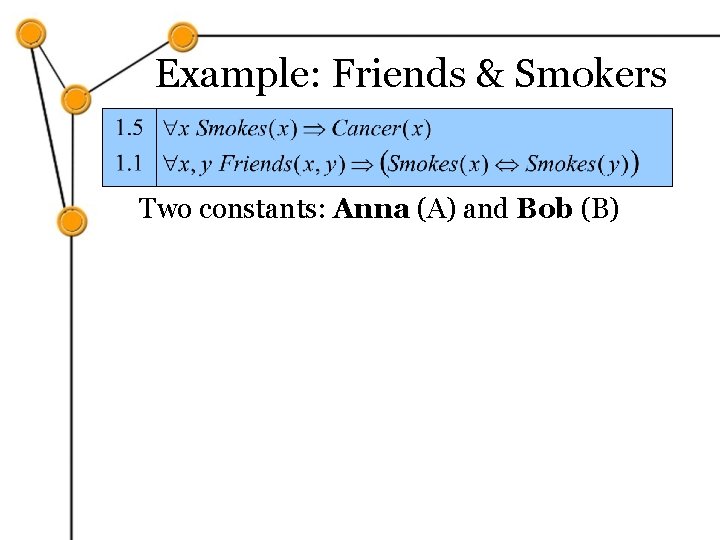
Example: Friends & Smokers

Example: Friends & Smokers

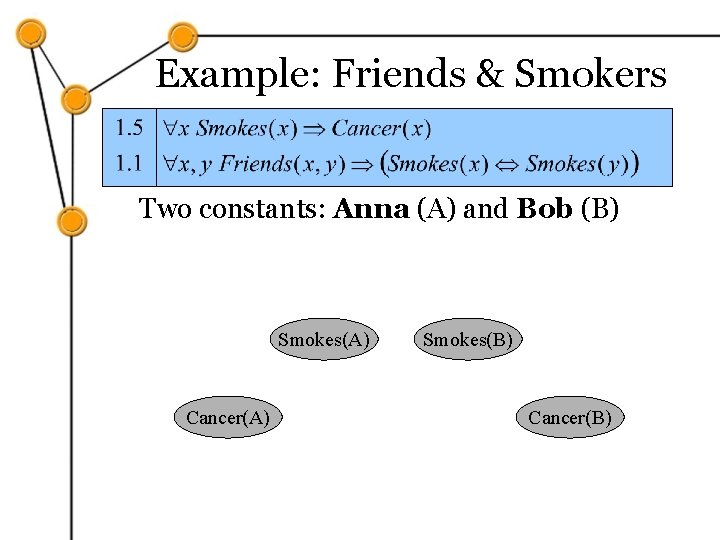
Example: Friends & Smokers

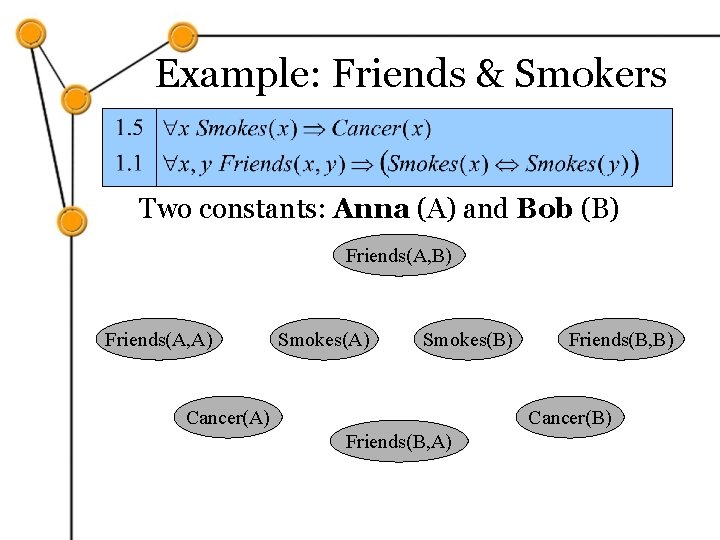
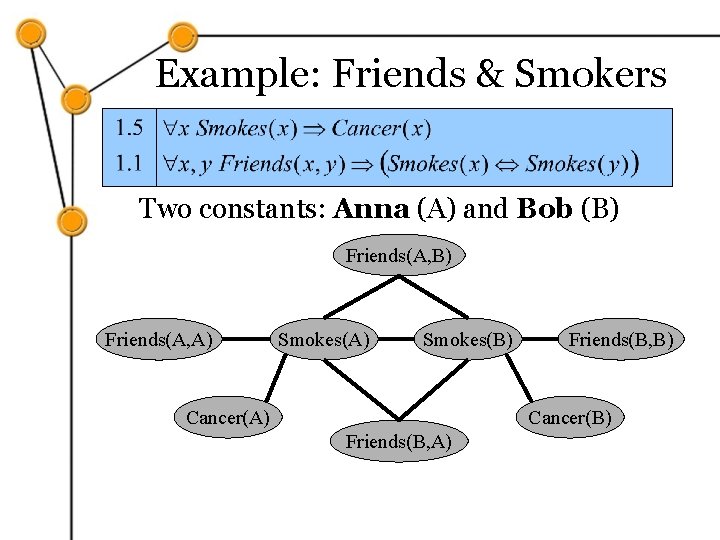
Example: Friends & Smokers Two constants: Anna (A) and Bob (B)

Example: Friends & Smokers Two constants: Anna (A) and Bob (B) Smokes(A) Cancer(A) Smokes(B) Cancer(B)

Example: Friends & Smokers Two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)

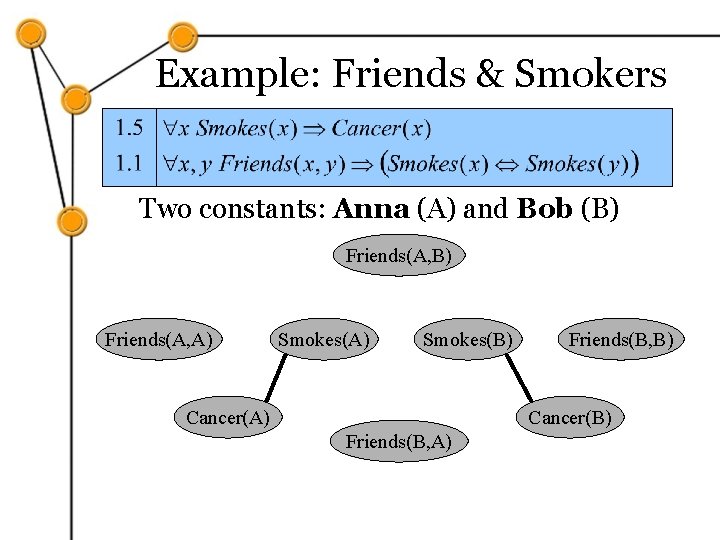
Example: Friends & Smokers Two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)

Example: Friends & Smokers Two constants: Anna (A) and Bob (B) Friends(A, A) Smokes(B) Cancer(A) Friends(B, B) Cancer(B) Friends(B, A)

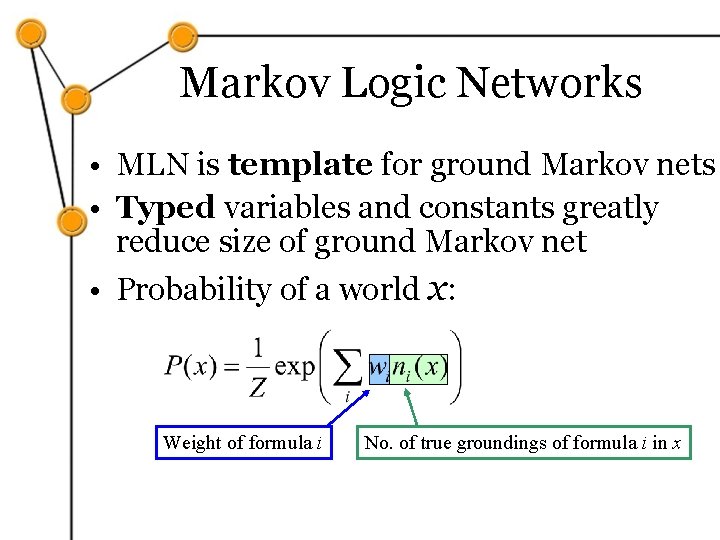
Markov Logic Networks • MLN is template for ground Markov nets • Typed variables and constants greatly reduce size of ground Markov net • Probability of a world x: Weight of formula i No. of true groundings of formula i in x

Markov Networks

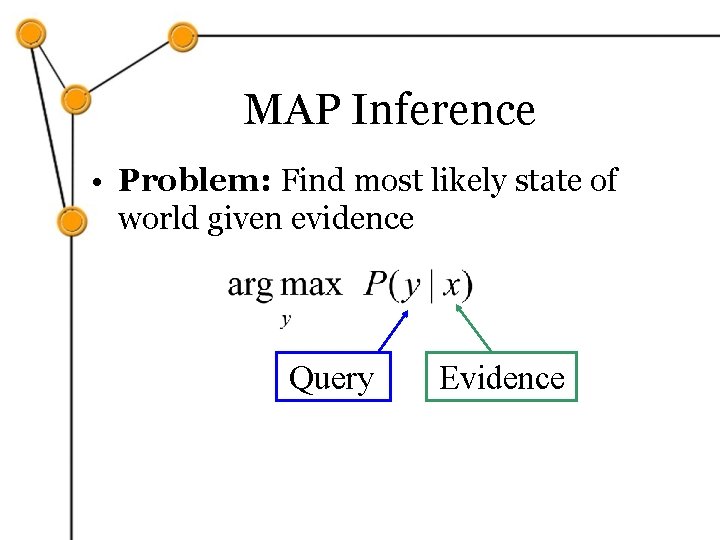
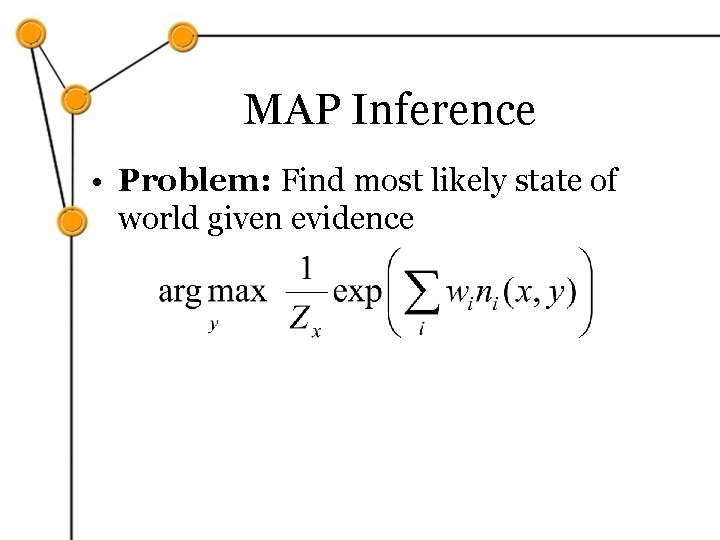
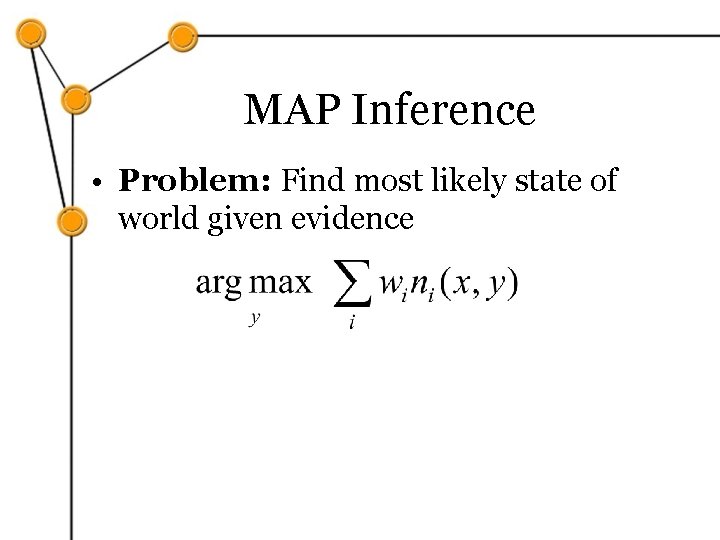
MAP Inference • Problem: Find most likely state of world given evidence Query Evidence

MAP Inference • Problem: Find most likely state of world given evidence

MAP Inference • Problem: Find most likely state of world given evidence

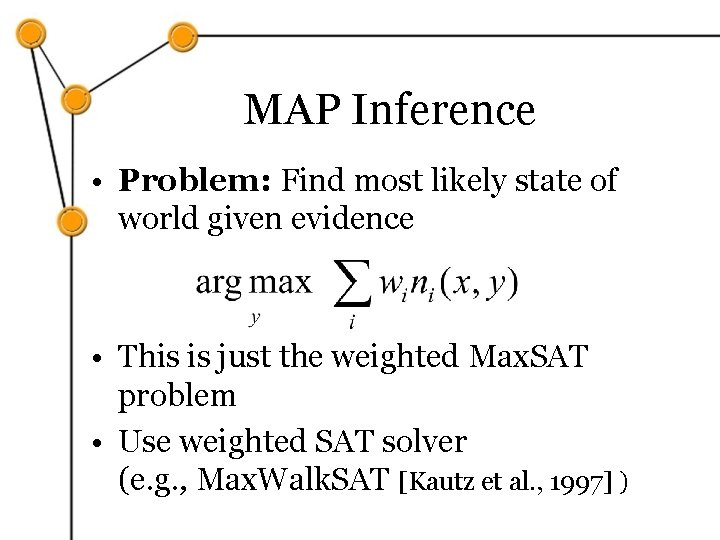
MAP Inference • Problem: Find most likely state of world given evidence • This is just the weighted Max. SAT problem • Use weighted SAT solver (e. g. , Max. Walk. SAT [Kautz et al. , 1997] )

The Max. Walk. SAT Algorithm for i : = 1 to max-tries do solution = random truth assignment for j : = 1 to max-flips do if weights(sat. clauses) > threshold then return solution c : = random unsatisfied clause with probability p flip a random variable in c else flip variable in c that maximizes weights(sat. clauses) return failure, best solution found

Computing Probabilities • P(Formula|MLN, C) = ? • Brute force: Sum probs. of worlds where formula holds • MCMC: Sample worlds, check formula holds • P(Formula 1|Formula 2, MLN, C) = ? • Discard worlds where Formula 2 does not hold • Slow! Can use Gibbs sampling instead

Weighted Learning • Given a formula without weights, we can learn them • Given a set with labeled instances, we want to find wi’s that maximize the sum of the features

References • P. Domingos & D. Lowd, Markov Logic: An Interface Layer for Artificial Intelligence, Synthesis Lectures on Artificial Intelligence and Machine Learning, Morgan & Claypool, 2009. • Most of the slides were taken from P. Domingos’ course website: http: //www. cs. washington. edu/homes/pedrod/803/ Thank You!