Markov Decision Processes CSE 6363 Machine Learning Vassilis

Markov Decision Processes CSE 6363 – Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1

A Sequential Decision Problem 3 +1 2 -1 1 START 1 2 3 4 2

A Sequential Decision Problem 3 +1 2 -1 1 START 1 2 3 4 3

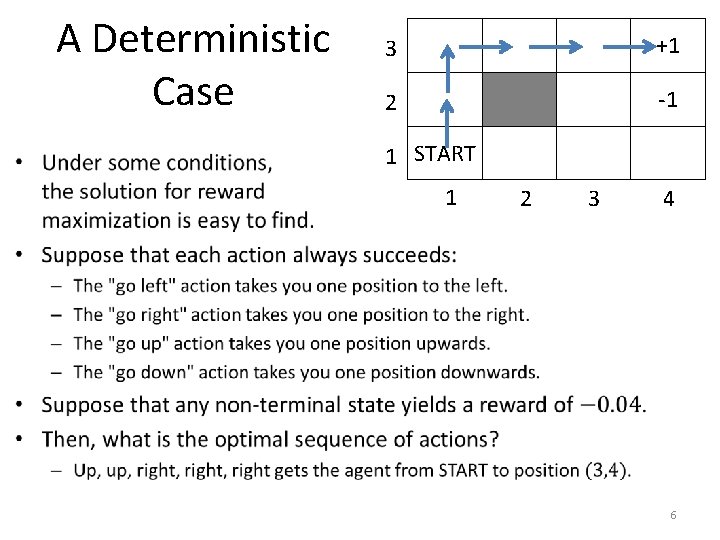
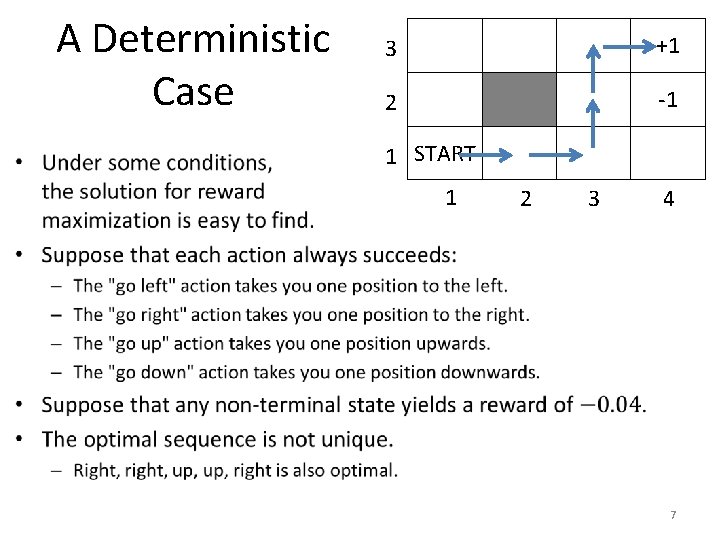
A Deterministic Case 3 +1 2 -1 1 START • Under some conditions, the solution for reward 1 maximization is easy to find. • Suppose that each action always succeeds: – – 2 3 4 The "go left" action takes you one position to the left. The "go right" action takes you one position to the right. The "go up" action takes you one position upwards. The "go down" action takes you one position downwards. • This situation is called deterministic. – A deterministic environment is an environment where the result of any action is known in advance. – A non-deterministic environment is an environment where the result of any action is not known in advance. 4

A Deterministic Case 3 +1 2 -1 1 START 1 2 3 4 5

A Deterministic Case 3 +1 2 -1 1 START 1 2 3 4 6

A Deterministic Case 3 +1 2 -1 1 START 1 2 3 4 7

A Deterministic Case 3 +1 2 -1 1 START 1 2 3 4 8

A Non. Deterministic Case • Under some conditions, life gets more complicated. • Suppose that each action: 3 +1 2 -1 1 START 1 2 3 4 – Succeeds with probability 0. 8. – Has a 0. 2 probability of moving to a direction that differs by 90 degrees from the intended direction. • For example: the "go up" action: – Has a probability of 0. 8 to take the agent one position upwards. – Has a probability of 0. 1 to take the agent one position to the left. – Has a probability of 0. 1 to take the agent one position to the right. 9

A Non. Deterministic Case 3 +1 2 -1 1 START 1 2 3 4 10

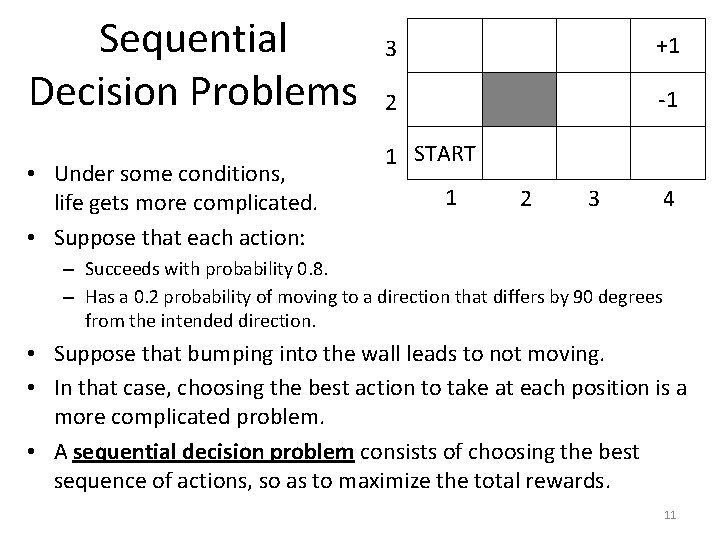
Sequential Decision Problems • Under some conditions, life gets more complicated. • Suppose that each action: 3 +1 2 -1 1 START 1 2 3 4 – Succeeds with probability 0. 8. – Has a 0. 2 probability of moving to a direction that differs by 90 degrees from the intended direction. • Suppose that bumping into the wall leads to not moving. • In that case, choosing the best action to take at each position is a more complicated problem. • A sequential decision problem consists of choosing the best sequence of actions, so as to maximize the total rewards. 11

Markov Decision Processes (MDPs) 3 +1 2 -1 1 START 1 2 3 4 12

A Transition Model Example • 3 +1 2 -1 1 START 1 2 3 4 13

A Transition Model Example • 3 +1 2 -1 1 START 1 2 3 4 14

A Transition Model Example • 3 +1 2 -1 1 START 1 2 3 4 15

A Transition Model Example • 3 +1 2 -1 1 START 1 2 3 4 16

A Transition Model Example • 3 +1 2 -1 1 START 1 2 3 4 17

A Transition Model Example • 3 +1 2 -1 1 START 1 2 3 4 18

A Transition Model Example • 3 +1 2 -1 1 START 1 2 3 4 19

A Transition Model Example • 3 +1 2 -1 1 START 1 2 3 4 20

A Transition Model Example • 3 +1 2 -1 1 START 1 2 3 4 21

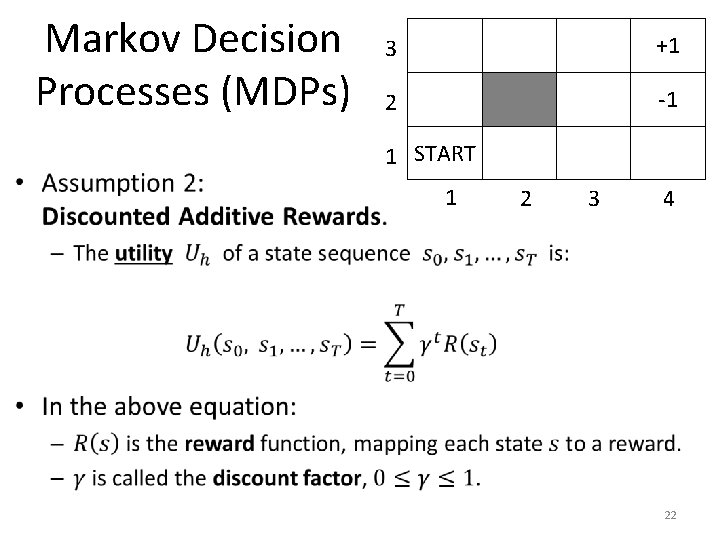
Markov Decision Processes (MDPs) 3 +1 2 -1 1 START 1 2 3 4 22

Discounted Additive Rewards 3 +1 2 -1 1 START 1 2 3 4 23

Discounted Additive Rewards 3 +1 2 -1 1 START 1 2 3 4 24

Discounted Additive Rewards 3 +1 2 -1 1 START 1 2 3 4 25

Discounted Additive Rewards 3 +1 2 -1 1 START 1 2 3 4 26

Discounted Additive Rewards 3 +1 2 -1 1 START 1 2 3 4 27

The MDP Problem 3 +1 2 -1 1 START 1 2 3 4 28

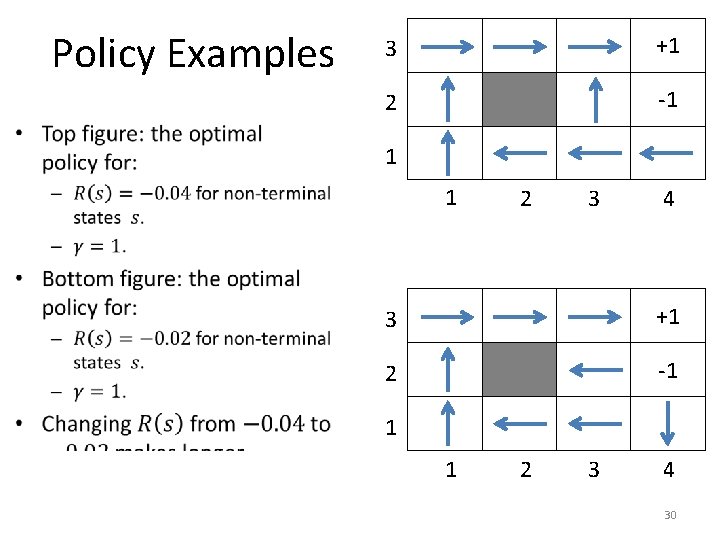
Policy Examples 3 +1 2 -1 1 1 2 3 4 29

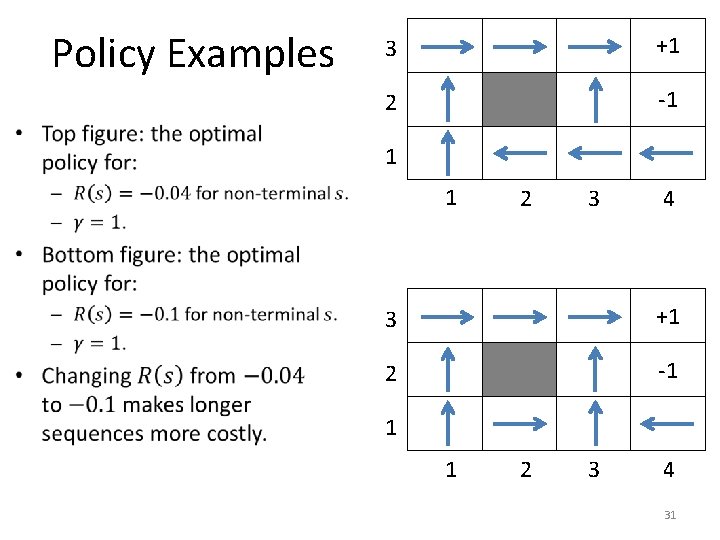
Policy Examples 3 +1 2 -1 1 1 2 3 4 30

Policy Examples 3 +1 2 -1 1 1 2 3 4 31

Utility of a State 3 +1 2 -1 1 START 1 2 3 4 32

A Note on Notation 3 +1 2 -1 1 START 1 2 3 4 33

Utility of a Sequence • 3 +1 2 -1 1 START 1 2 3 4 34

Utility of a Sequence • 3 +1 2 -1 1 START 1 2 3 4 35

Utility of a State • 2 +1 1 START 1 -1 2 36

Utility of a State • 2 +1 1 START 1 -1 2 37

Utility of a State • 2 +1 1 START 1 -1 2 38

Utility of a State • 2 +1 1 START 1 -1 2 39

Utility of a State • 2 +1 1 START 1 -1 2 40

Utility of a State • 2 +1 1 START 1 -1 2 41

Utility of a State • 2 +1 1 START 1 -1 2 42

Utility of a State • 2 +1 1 START 1 -1 2 43

Utility of a State • 2 +1 1 START 1 -1 2 44

Utility of a State • 2 +1 1 START 1 -1 2 45

Utility of a State • 2 +1 1 START 1 -1 2 46

Utility of a State • 2 +1 1 START 1 -1 2 47

Utility of a State • 2 +1 1 START 1 -1 2 48

Utility of a State • 2 +1 1 START 1 -1 2 49

Utility of a State • 2 +1 1 START 1 -1 2 50

Utility of a State • 2 +1 1 START 1 -1 2 51

Utility of a State • 2 +1 1 START 1 -1 2 52

Utility of a State 2 +1 1 START 1 -1 2 • 53

Utility of a State 2 +1 1 START 1 -1 2 • 54

Utility of a State 2 +1 1 START 1 -1 2 • 55

The Bellman Equation 2 +1 1 START 1 -1 2 • Combining these equations together, we get: • This equation is called the Bellman equation. 56

The Bellman Equation 2 +1 1 START 1 -1 2 • 57

The Value Iteration Algorithm • 58

The Value Iteration Algorithm • 59

The Value Iteration Algorithm • We will skip the proof, but it can be proven that this algorithm converges to the correct solutions of the Bellman equations. – Details can be found in S. Russell and P. Norvig, "Artificial Intelligence: A Modern Approach", third edition (2009), Prentice Hall. 60

The Value Iteration Algorithm • 61

The Value Iteration Algorithm • So, the value iteration algorithm can be summarized as follows: – Initialize utilities of states to zero values. – Repeat updating utilities of states using Bellman updates, until the estimated values converge. 62

A Value Iteration Example • 3 +1 2 -1 1 START 1 2 3 4 3 0 0 2 0 0 0 1 2 3 4 Utility Values 63

A Value Iteration Example • 3 +1 2 -1 1 START 1 3 -0. 04 2 3 4 -0. 04 +1 -0. 04 2 3 4 2 -0. 04 1 Utility Values 64

A Value Iteration Example • 3 +1 2 -1 1 START 1 3 -0. 08 2 3 4 -0. 08 0. 67 +1 -0. 08 2 3 4 2 -0. 08 1 Utility Values 65

A Value Iteration Example • 3 +1 2 -1 1 START 1 3 -0. 11 2 3 4 0. 43 0. 73 +1 0. 35 -1 -0. 11 2 3 4 2 -0. 11 1 Utility Values 66

A Value Iteration Example • 3 +1 2 -1 1 START 3 1 2 3 4 0. 25 0. 57 0. 78 +1 0. 43 -1 -0. 14 0. 19 -0. 14 2 3 4 2 -0. 14 1 Utility Values 67

A Value Iteration Example • 3 +1 2 -1 1 START 1 2 3 4 3 0. 38 0. 62 0. 79 +1 2 0. 12 0. 47 -1 0. 07 0. 24 -0. 01 2 3 4 1 -0. 16 1 Utility Values 68

A Value Iteration Example • 3 +1 2 -1 1 START 1 2 3 4 3 0. 45 0. 64 0. 79 +1 2 0. 25 0. 48 -1 1 0. 04 0. 15 0. 30 0. 05 1 2 3 4 Utility Values 69

A Value Iteration Example • 3 +1 2 -1 1 START 1 2 3 4 3 0. 48 0. 65 0. 79 +1 2 0. 33 0. 48 -1 1 0. 16 0. 21 0. 32 0. 09 1 2 3 4 Utility Values 70

A Value Iteration Example • 3 +1 2 -1 1 START 1 2 3 4 3 0. 50 0. 65 0. 80 +1 2 0. 37 0. 49 -1 1 0. 23 0. 34 0. 11 1 2 3 4 Utility Values 71

A Value Iteration Example • 3 +1 2 -1 1 START 1 2 3 4 3 0. 51 0. 65 0. 80 +1 2 0. 40 0. 49 -1 1 0. 30 0. 25 0. 34 0. 13 1 2 3 4 Utility Values 72

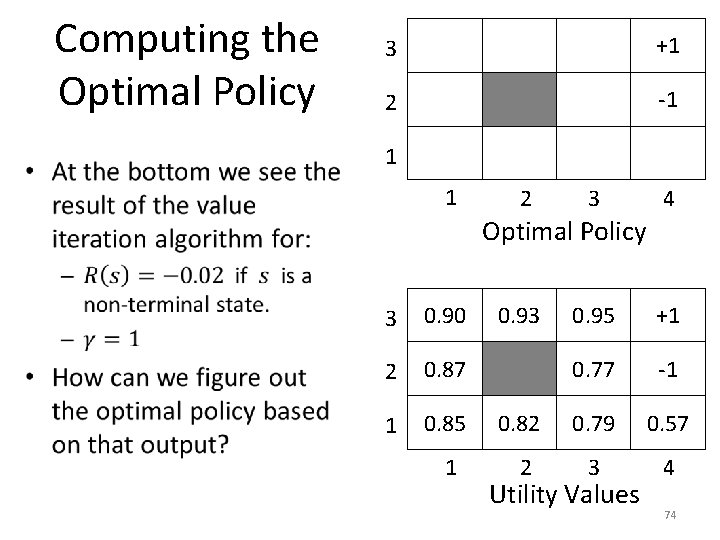
Computing the Optimal Policy • 73

Computing the Optimal Policy • 3 +1 2 -1 1 1 2 3 4 Optimal Policy 3 0. 90 2 0. 87 1 0. 85 1 0. 93 0. 95 +1 0. 77 -1 0. 82 0. 79 0. 57 2 3 4 Utility Values 74

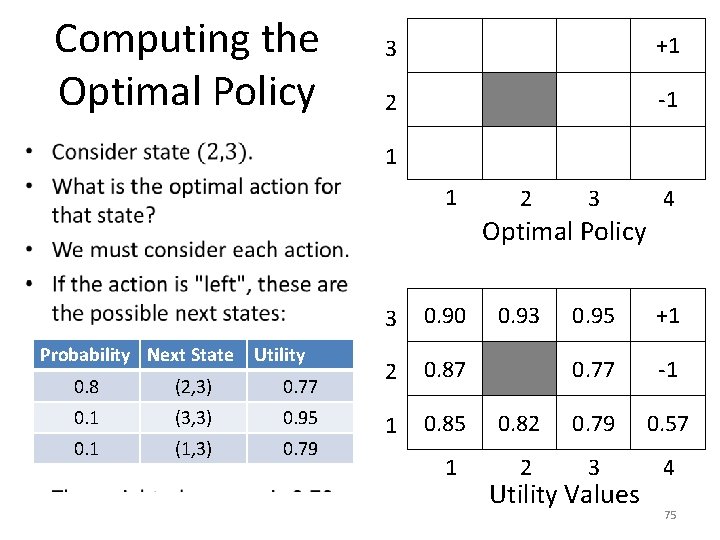
Computing the Optimal Policy • 3 +1 2 -1 1 1 2 3 4 Optimal Policy Probability Next State Utility 0. 8 (2, 3) 0. 77 0. 1 (3, 3) 0. 95 0. 1 (1, 3) 0. 79 3 0. 90 2 0. 87 1 0. 85 1 0. 93 0. 95 +1 0. 77 -1 0. 82 0. 79 0. 57 2 3 4 Utility Values 75

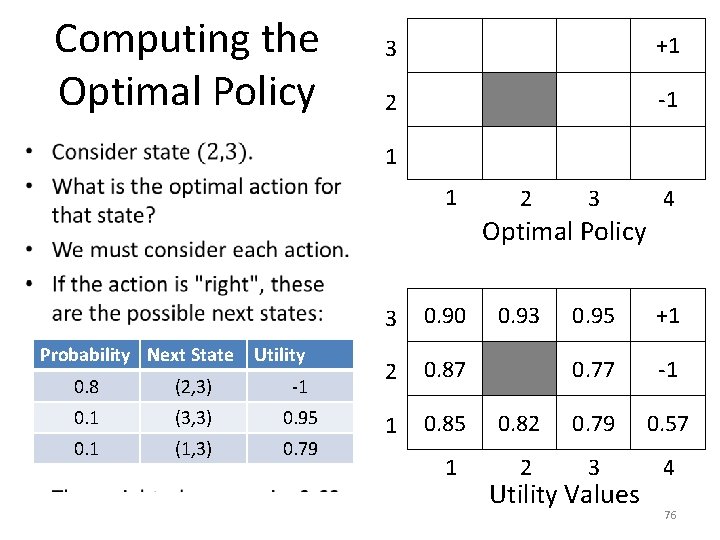
Computing the Optimal Policy • 3 +1 2 -1 1 1 2 3 4 Optimal Policy Probability Next State Utility 0. 8 (2, 3) -1 0. 1 (3, 3) 0. 95 0. 1 (1, 3) 0. 79 3 0. 90 2 0. 87 1 0. 85 1 0. 93 0. 95 +1 0. 77 -1 0. 82 0. 79 0. 57 2 3 4 Utility Values 76

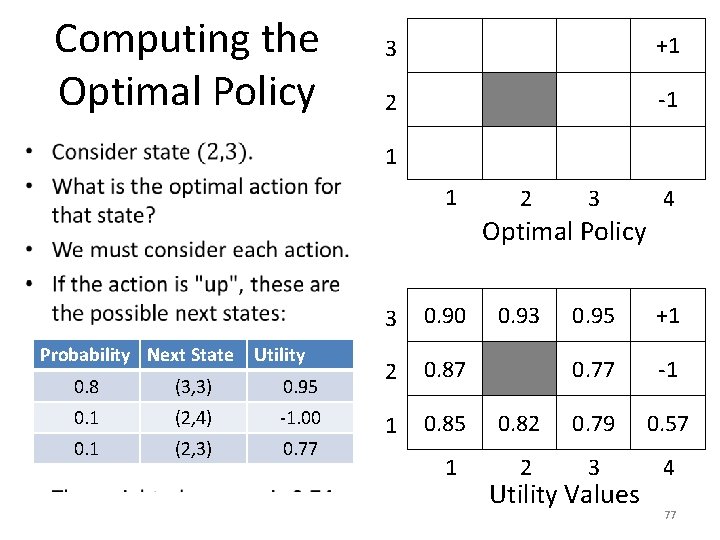
Computing the Optimal Policy • 3 +1 2 -1 1 1 2 3 4 Optimal Policy Probability Next State Utility 0. 8 (3, 3) 0. 95 0. 1 (2, 4) -1. 00 0. 1 (2, 3) 0. 77 3 0. 90 2 0. 87 1 0. 85 1 0. 93 0. 95 +1 0. 77 -1 0. 82 0. 79 0. 57 2 3 4 Utility Values 77

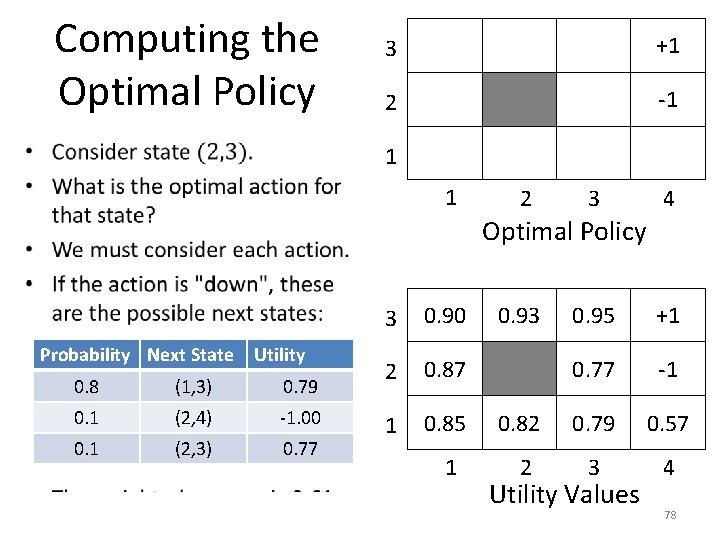
Computing the Optimal Policy • 3 +1 2 -1 1 1 2 3 4 Optimal Policy Probability Next State Utility 0. 8 (1, 3) 0. 79 0. 1 (2, 4) -1. 00 0. 1 (2, 3) 0. 77 3 0. 90 2 0. 87 1 0. 85 1 0. 93 0. 95 +1 0. 77 -1 0. 82 0. 79 0. 57 2 3 4 Utility Values 78

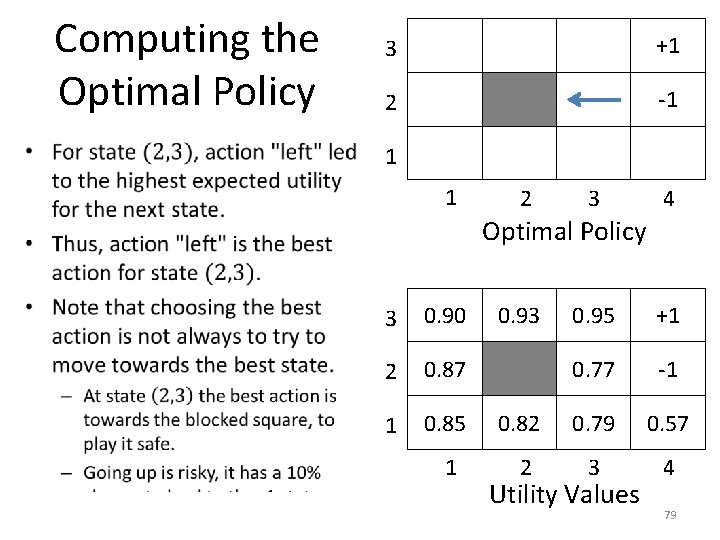
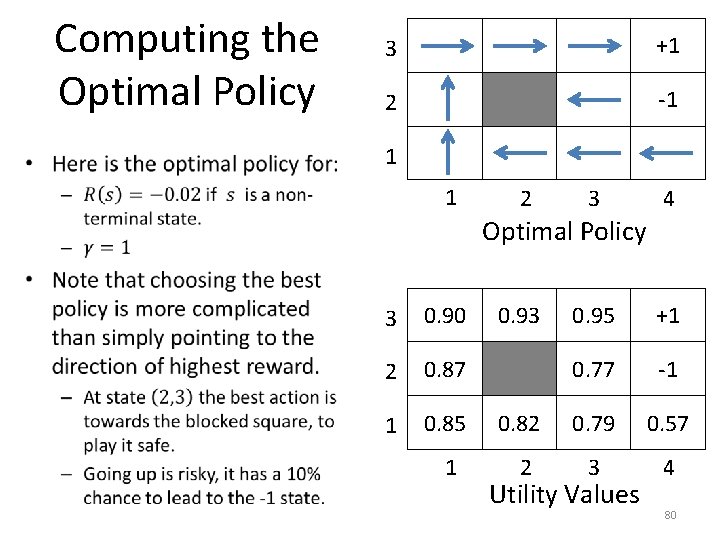
Computing the Optimal Policy • 3 +1 2 -1 1 1 2 3 4 Optimal Policy 3 0. 90 2 0. 87 1 0. 85 1 0. 93 0. 95 +1 0. 77 -1 0. 82 0. 79 0. 57 2 3 4 Utility Values 79

Computing the Optimal Policy • 3 +1 2 -1 1 1 2 3 4 Optimal Policy 3 0. 90 2 0. 87 1 0. 85 1 0. 93 0. 95 +1 0. 77 -1 0. 82 0. 79 0. 57 2 3 4 Utility Values 80

The Policy Iteration Algorithm • 81

The Policy Iteration Algorithm • 82

The Policy Iteration Algorithm • To be able to implement the policy iteration algorithm, we need to specify how to carry out each of the two steps of the main loop: – Policy evaluation. – Policy improvement. 83

The Policy Evaluation Step • 84

The Policy Evaluation Step • 85

The Policy Evaluation Step • 86

The Policy Evaluation Step • 87

The Policy Iteration Algorithm • 88

The Policy Iteration Algorithm • The main loop alternates between: • Updating the utilities given the policy. • Updating the policy given the utilities. The main loop exits when the policy stops changing. 89

The Policy Iteration Algorithm • The main loop alternates between: • Updating the utilities given the policy. • Updating the policy given the utilities. The main loop exits when the policy stops changing. 90

The Policy Iteration Algorithm • The main loop alternates between: • Updating the utilities given the policy. • Updating the policy given the utilities. The main loop exits when the policy stops changing. 91

Markov Decision Processes: Recap • 92

Markov Decision Processes: Recap • The value iteration algorithm computes the utility of each state using an iterative approach. – Once the utilities of all states have been computed, the optimal policy is defined by identifying, for each state, the action leading to the highest expected utility. • The policy iteration algorithm is a more efficient alternative, at the cost of possibly losing some accuracy. – It computes the optimal policy directly, without computing exact values for the utilities. – Utility values are updated for a few rounds only, and not until convergence. 93