Markov Cluster Algorithm Outline Introduction Important MCL The

Markov Cluster Algorithm

Outline � Introduction � Important � MCL � The Concepts in MCL Algorithm Features of MCL Algorithm � Summary

Graph Clustering � Intuition: ◦ High connected nodes could be in one cluster ◦ Low connected nodes could be in different clusters. � Model: ◦ A random walk may start at any node ◦ Starting at node r, if a random walk will reach node t with high probability, then r and t should be clustered together.

Markov Clustering (MCL) � Markov process ◦ The probability that a random will take an edge at node u only depends on u and the given edge. ◦ It does not depend on its previous route. ◦ This assumption simplifies the computation.

MCL � Flow network is used to approximate the partition � There is an initial amount of flow injected into each node. � At each step, a percentage of flow will goes from a node to its neighbors via the outgoing edges.

MCL � Edge Weight ◦ Similarity between two nodes ◦ Considered as the bandwidth or connectivity. ◦ If an edge has higher weight than the other, then more flow will be flown over the edge. ◦ The amount of flow is proportional to the edge weight. ◦ If there is no edge weight, then we can assign the same weight to all edges.

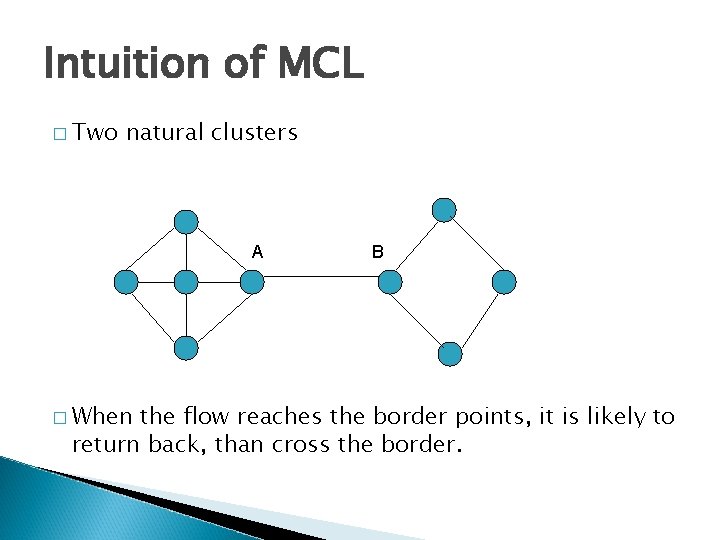
Intuition of MCL � Two natural clusters A � When B the flow reaches the border points, it is likely to return back, than cross the border.

MCL � When the flow reaches A, it has four possible outcomes. ◦ Three back into the cluster, one leak out. ◦ ¾ of flow will return, only ¼ leaks. � Flow will accumulate in the center of a cluster (island). � The border nodes will starve.

Introduction—MCL in General � Simualtion � Two of Random Flow in graph Operations: Expansion and Inflation � Intrinsic relationship between MCL process result and cluster structure

Introduction-Cluster � Popular that Description: partition into graph so � Intra-partition similarity is the highest � Inter-partition similarity is the lowest

Introduction-Cluster � Observation 1: number of Higher-Length paths in G is large for pairs of vertices lying in the same dense cluster � The � Small for pairs of vertices belonging to different clusters

Introduction-Cluster � Oberservation �A 2: Random Walk in G that visits a dense cluster will likely not leave the cluster until many of its vertices have been visited

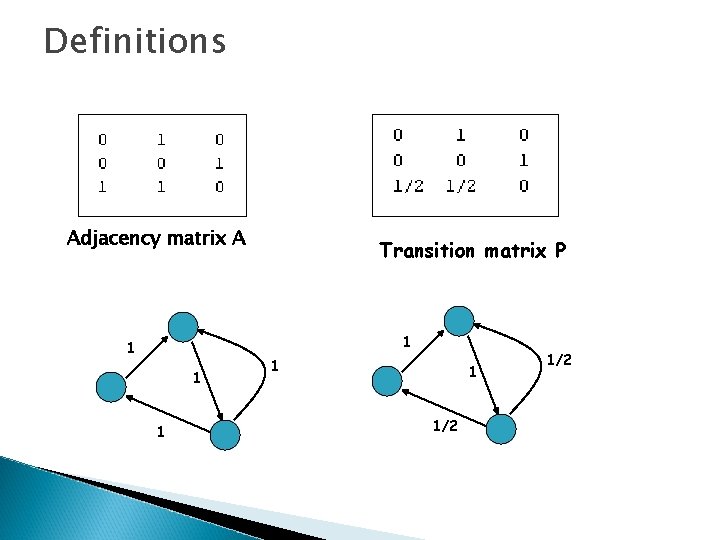
Definitions � nxn Adjacency matrix A. ◦ A(i, j) = weight on edge from i to j ◦ If the graph is undirected A(i, j)=A(j, i), i. e. A is symmetric � nxn Transition matrix P. ◦ P is row stochastic ◦ P(i, j) = probability of stepping on node j from node i = A(i, j)/∑i. A(i, j) � nxn Laplacian Matrix L. ◦ L(i, j)=∑i. A(i, j)-A(i, j) ◦ Symmetric positive semi-definite for undirected graphs ◦ Singular

Definitions Adjacency matrix A Transition matrix P 1 1 1 1/2

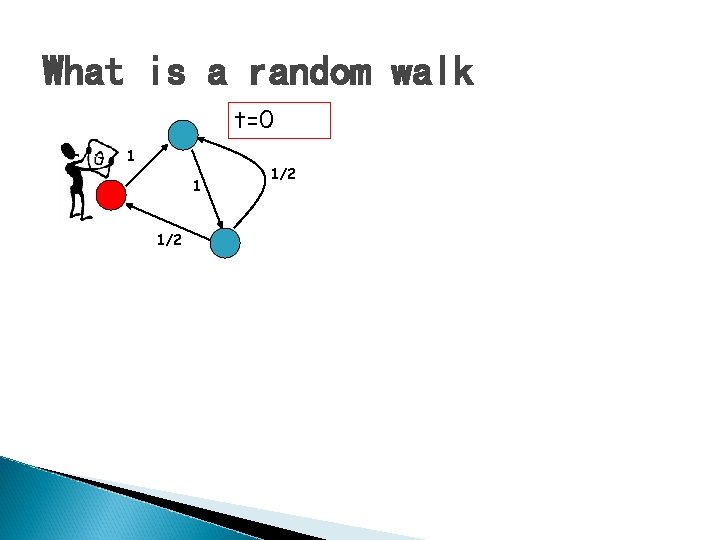
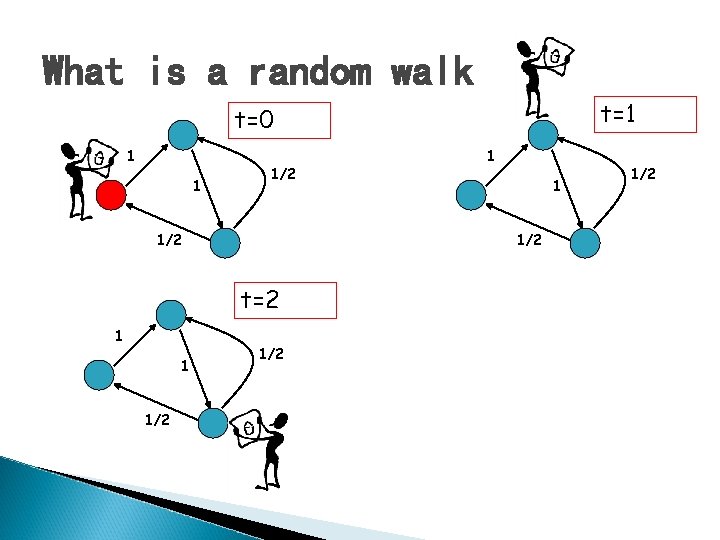
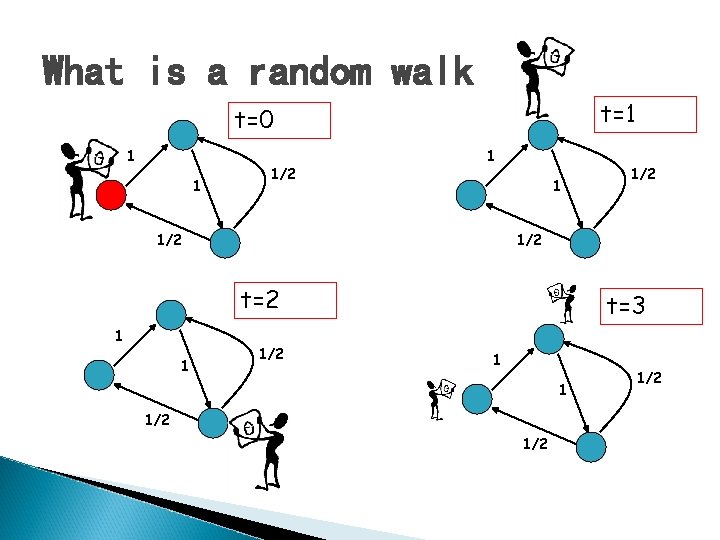
What is a random walk t=0 1 1 1/2

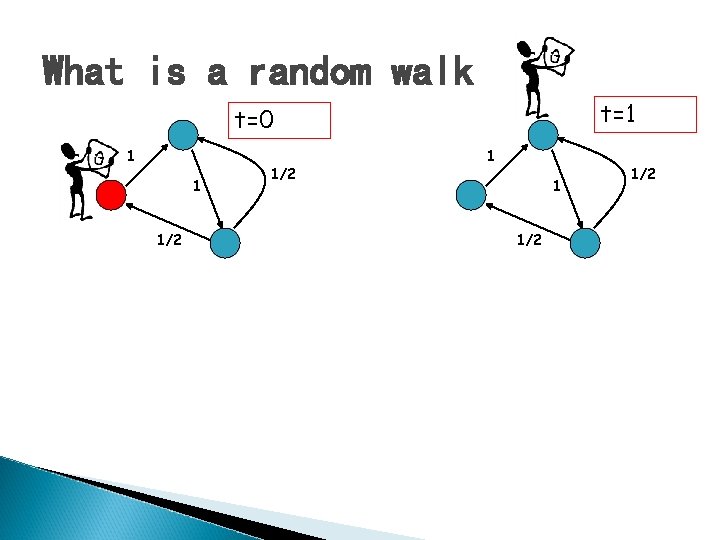
What is a random walk t=1 t=0 1 1 1/2 1/2

What is a random walk t=1 t=0 1 1 1/2 t=2 1 1 1/2

What is a random walk t=1 t=0 1 1 1/2 1/2 t=2 1 1 1/2 t=3 1 1 1/2 1/2

Probability Distributions � � xt(i) = probability that the surfer is at node i at time t xt+1(i) = ∑j(Probability of being at node j)*Pr(j->i) =∑jxt(j)*P(j, i) xt+1 = xt. P = xt-1*P*P= xt-2*P*P*P = …=x 0 Pt What happens when the surfer keeps walking for a long time?

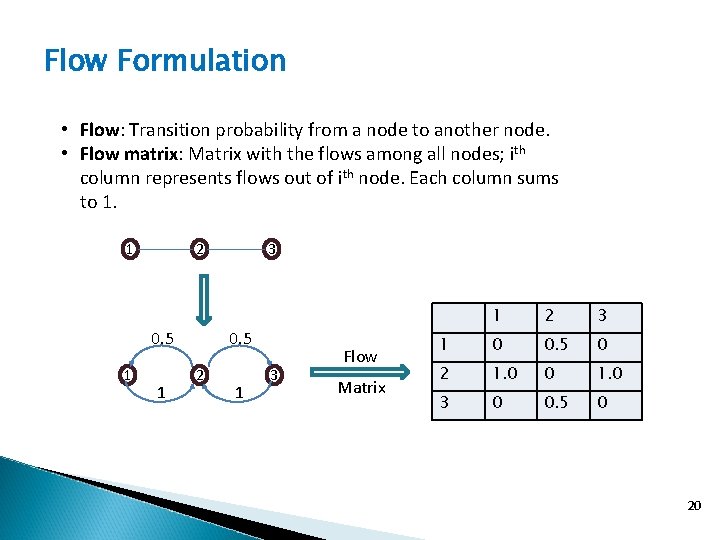
Flow Formulation • Flow: Transition probability from a node to another node. • Flow matrix: Matrix with the flows among all nodes; ith column represents flows out of ith node. Each column sums to 1. 1 2 0. 5 1 1 3 0. 5 2 1 3 Flow Matrix 1 2 3 1 0 0. 5 0 2 1. 0 0 1. 0 3 0 0. 5 0 20

Motivation behind MCL � Measure or Sample any of these—high-length paths, random walks and deduce the cluster structure from the behavior of the samples quantities. � Cluster structure will show itself as a peaked distribution of the quantities �A lack of cluster structure will result in a flat distribution

Important Concepts about MCL � Markov Chain � Random � Some Walk on Graph Definitions in MCL

Markov Chain �A Random Process with Markov Property: given the present state, future states are independent of the past states � Markov � At each step the process may change its state from the current state to another state, or remain in the same state, according to a certain probability distribution.

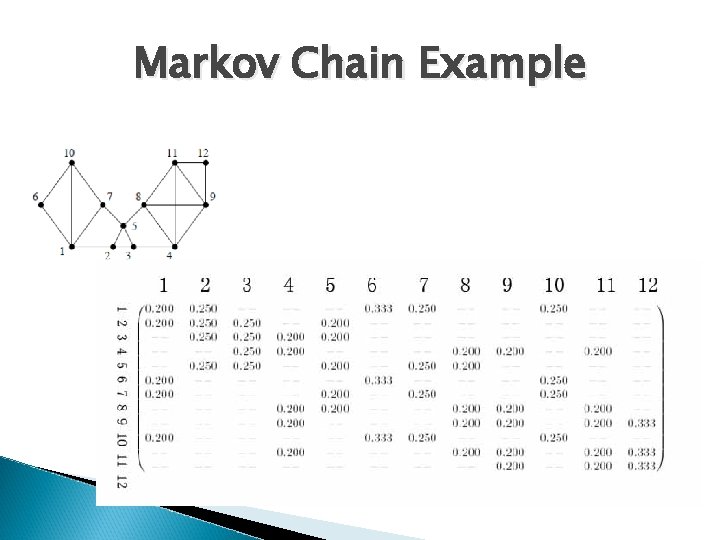
Markov Chain Example

Random Walk on Graph �A walker takes off on some arbitrary vertex � He successively visits new vertices by selecting arbitrarily one of outgoing edges � There is not much difference between random walk and finite Markov chain.

Some Definitions in MCL � Simple Graph graph is undirected graph in which every nonzero weight equals 1.

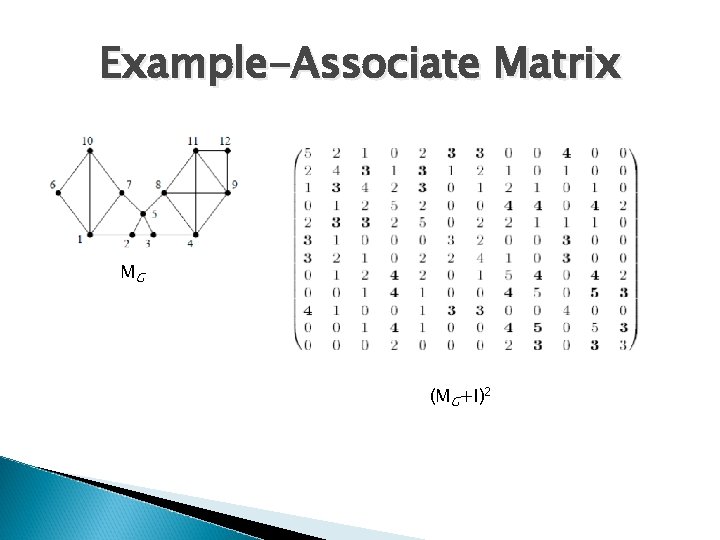
Some Definitions in MCL � Associated � The Matrix associated matrix of G, denoted MG , is defined by setting the entry (MG)pq equal to w(vp, vq)

Some Definitions in MCL � Markov � The Matrix Markov matrix associated with a graph G is denoted by TG and is formally defined by letting its qth column be the qth column of M normalized

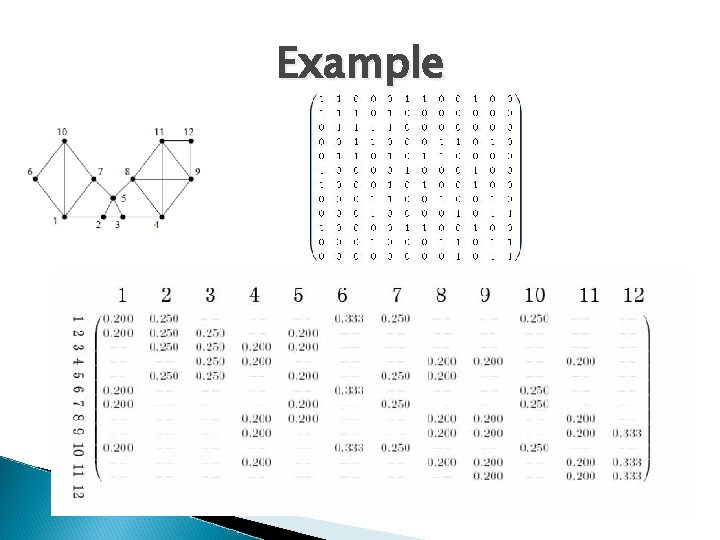
Example

Explanation to Previous Example � The associate matrix and markov matrix is actually for matrix M+I �I denotes diagonal matrix with nonzero element equals 1 � Adding a loop to every vertex of the graph because for a walker it is possible that he will stay in the same place in his next step

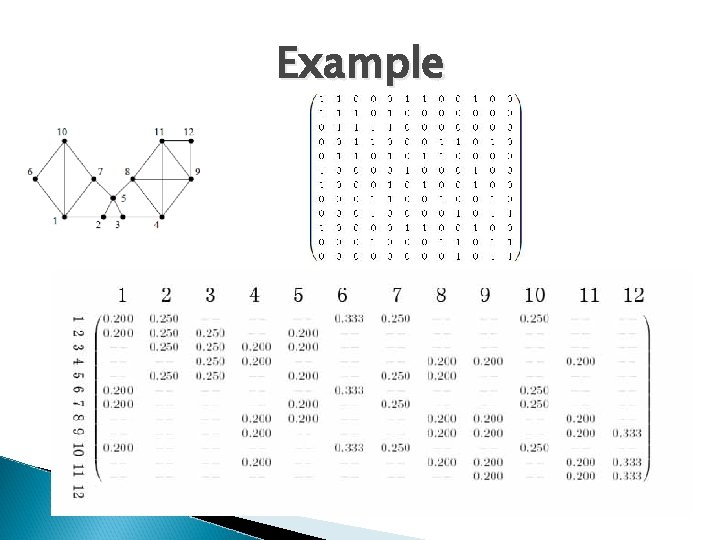
Example

Markov Cluster Algorithm � Find � Start Higher-Length Path Point: In associated matrix that the quantity (Mk)pq has a straightforward interpretation as the number of paths of length k between vp and vq

Example-Associate Matrix MG (MG+I)2

Example- Markvo Matrix MG

Example-Markov Matrix

Conclusion � Flow is easier with dense regions than across sparse boundaries, � However, in the long run, this effect disappears. � Power of matrix can be used to find higherlength path but the effect will diminish as the flow goes on.

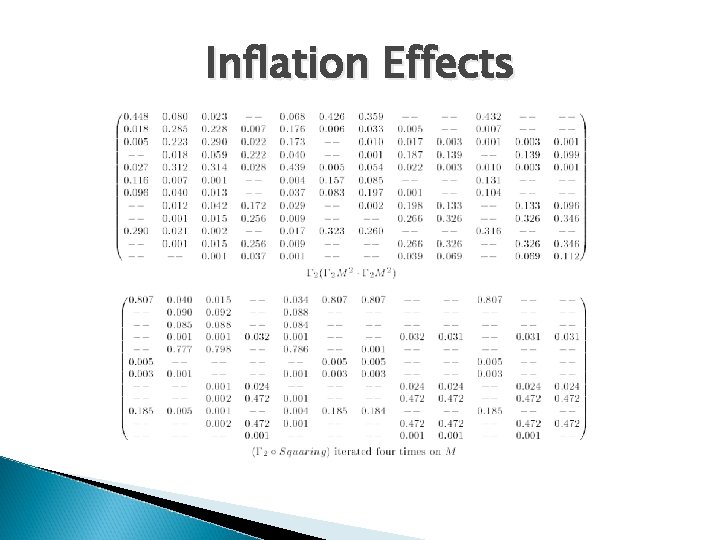
Inflation Operation How can we change the distribution of transition probabilities such that prefered neighbours are further favoured and less popular neighbours are demoted. � Idea: � MCL Solution: raise all the entries in a given column to a certain power greater than 1 (e. g. squaring) and rescaling the column to have the sum 1 again.

Example for Inflation Operation

Definition for Inflation Operation

Apply Inflation Operation to the previous Markov Matrix

Inflation Effects

MCL Opeartions � Expansion Operation: power of matrix, expansion of dense region � Inflation Operation: mention aboved, elimination of unfavoured region

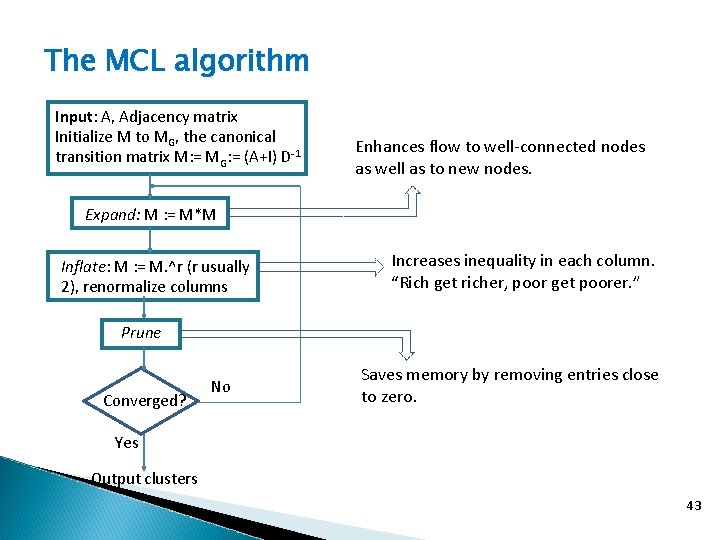
The MCL algorithm Input: A, Adjacency matrix Initialize M to MG, the canonical transition matrix M: = MG: = (A+I) D-1 Enhances flow to well-connected nodes as well as to new nodes. Expand: M : = M*M Inflate: M : = M. ^r (r usually 2), renormalize columns Increases inequality in each column. “Rich get richer, poor get poorer. ” Prune Converged? No Saves memory by removing entries close to zero. Yes Output clusters 43

Multi-level Regularized MCL Run R-MCL to convergence, output clusters. Input Graph Coarsen Run Curtailed R-MCL, project flow. Intermediate Graph Coarsen Intermediate Graph. . . Coarsen . . . Initializes flow matrix of refined graph Run Curtailed R-MCL, project flow. Captures global topology of graph Coarsest Graph Faster to run on smaller graphs first 44

Markov Cluster Algorithm

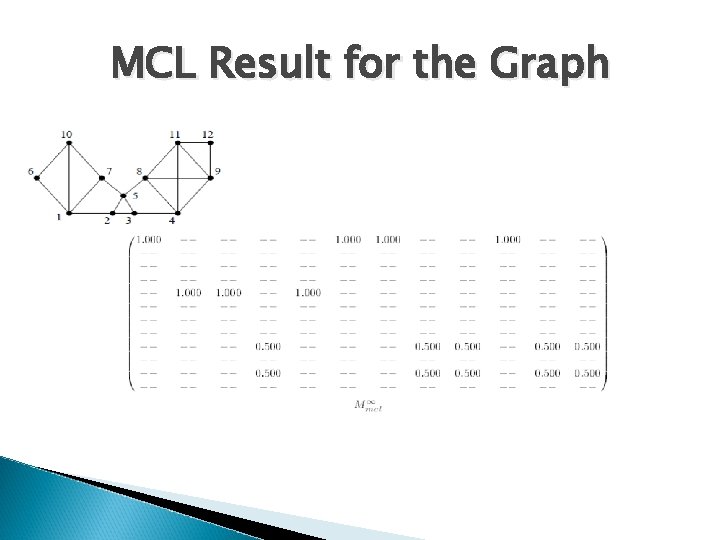
MCL Result for the Graph

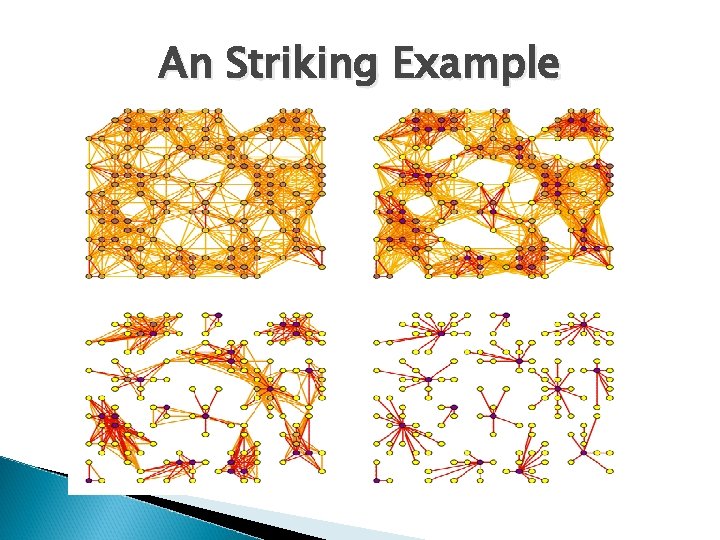
An Striking Example

Striking Animation � http: //www. micans. org/mcl/ani/mcl- animation. html

Mapping nonnegative idempotent matrces onto clusters � Find attractor: the node a is an attractor if Maa is nonzero � Find attractor system: If a is an attractor then the set of its neighbours is called an attractor system. � If there is a node who has arc connected to any node of an attractor system, the node will belong to the same cluster as that attractor system.

Example Attractor Set={1, 2, 3, 4, 5, 6, 7, 8, 9, 10} The Attractor System is {1, 2, 3}, {4, 5, 6, 7}, {8, 9}, {10} The overlapping clusters are {1, 2, 3, 11, 12, 15}, {4, 5, 6, 7, 13}, {8, 9, 12, 13, 14, 15}, {10, 12, 13}

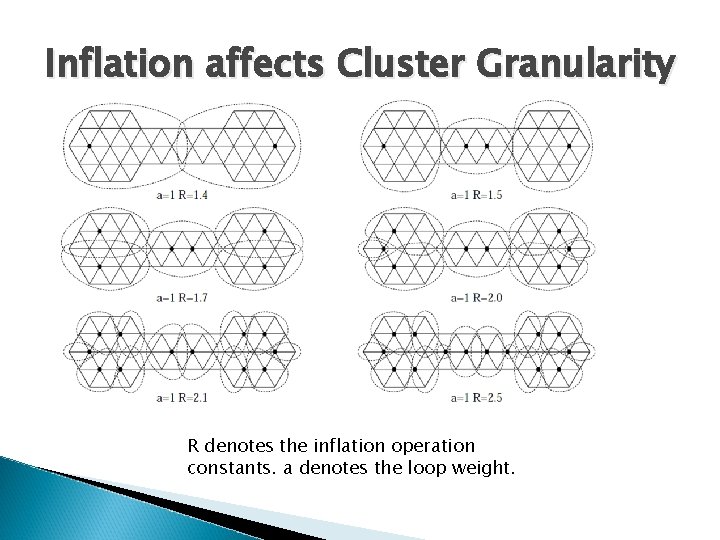
MCL Feature � how many steps are requred before the algorithm converges to a idempoent matrix? � The number is typically somewhere between 10 and 100 � The effect of inflation on cluster granularity

Inflation affects Cluster Granularity R denotes the inflation operation constants. a denotes the loop weight.

Summary � MCL stimulates random walk on graph to find cluster � Expansion promotes dense region while Inflation demotes the less favoured region � There is intrinsic relationship between MCL result and cluster structure