Markov Cluster Algorithm Liang Ge Outline Introduction Important

Markov Cluster Algorithm Liang Ge

Outline � Introduction � Important � MCL � The Concepts in MCL Algorithm Features of MCL Algorithm � Summary

Introduction—MCL in General � Simualtion � Two of Random Flow in graph Operations: Expansion and Inflation � Intrinsic relationship between MCL process result and cluster structure

Introduction-Cluster � Popular that Description: partition into graph so � Intra-partition similarity is the highest � Inter-partition similarity is the lowest

Introduction-Cluster � Observation 1: number of Higher-Length paths in G is large for pairs of vertices lying in the same dense cluster � The � Small for pairs of vertices belonging to different clusters

Introduction-Cluster � Oberservation �A 2: Random Walk in G that visits a dense cluster will likely not leave the cluster until many of its vertices have been visited

Motivation behind MCL � Measure or Sample any of these—high-length paths, random walks and deduce the cluster structure from the behavior of the samples quantities. � Cluster structure will show itself as a peaked distribution of the quantities �A lack of cluster structure will result in a flat distribution

Important Concepts about MCL � Markov Chain � Random � Some Walk on Graph Definitions in MCL

Markov Chain �A Random Process with Markov Property: given the present state, future states are independent of the past states � Markov � At each step the process may change its state from the current state to another state, or remain in the same state, according to a certain probability distribution.

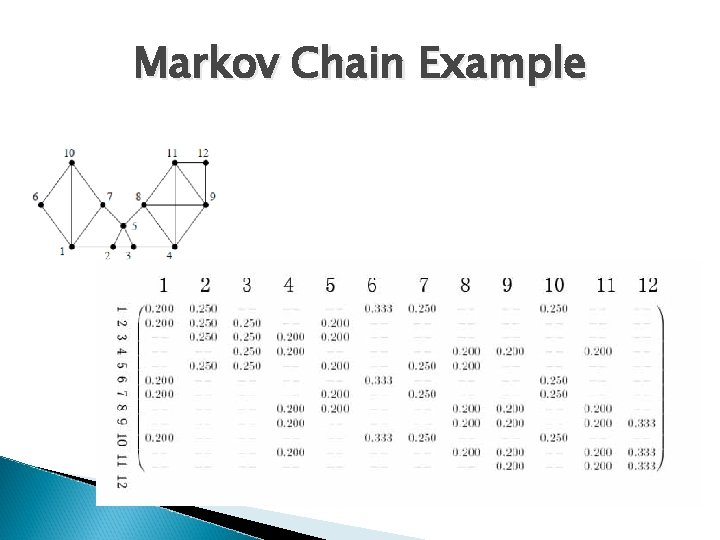
Markov Chain Example

Random Walk on Graph �A walker takes off on some arbitrary vertex � He successively visits new vertices by selecting arbitrarily one of outgoing edges � There is not much difference between random walk and finite Markov chain.

Some Definitions in MCL � Simple Graph graph is undirected graph in which every nonzero weight equals 1.

Some Definitions in MCL � Associated � The Matrix associated matrix of G, denoted MG , is defined by setting the entry (MG)pq equal to w(vp, vq)

Some Definitions in MCL � Markov � The Matrix Markov matrix associated with a graph G is denoted by TG and is formally defined by letting its qth column be the qth column of M normalized

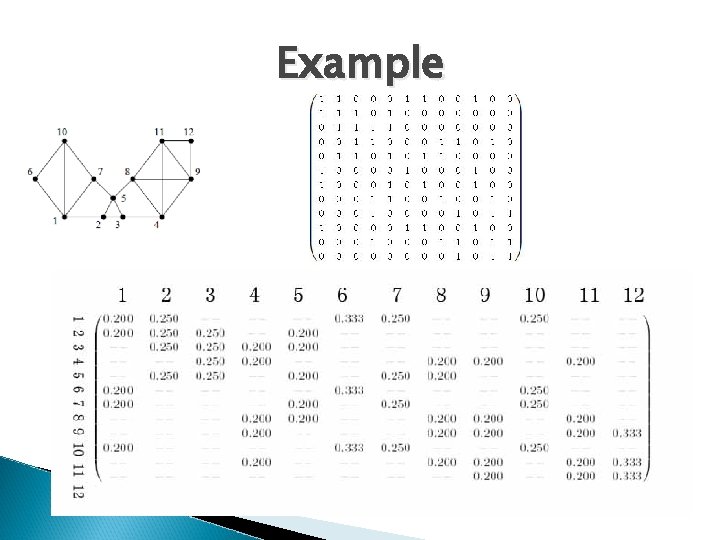
Example

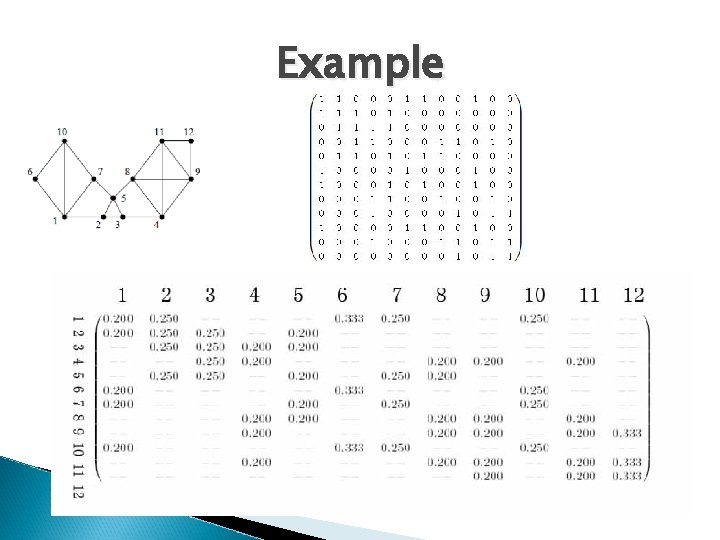
Explanation to Previous Example � The associate matrix and markov matrix is actually for matrix M+I �I denotes diagonal matrix with nonzero element equals 1 � Adding a loop to every vertex of the graph because for a walker it is possible that he will stay in the same place in his next step

Example

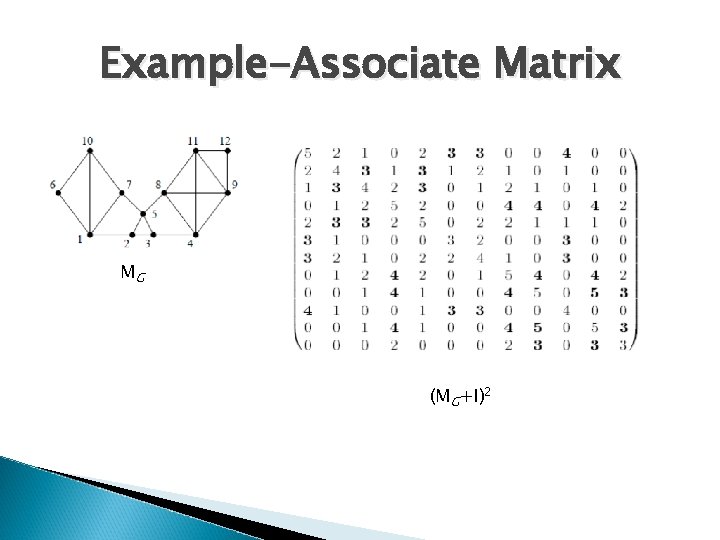
Markov Cluster Algorithm � Find � Start Higher-Length Path Point: In associated matrix that the quantity (Mk)pq has a straightforward interpretation as the number of paths of length k between vp and vq

Example-Associate Matrix MG (MG+I)2

Example- Markvo Matrix MG

Example-Markov Matrix

Conclusion � Flow is easier with dense regions than across sparse boundaries, � However, in the long run, this effect disappears. � Power of matrix can be used to find higherlength path but the effect will diminish as the flow goes on.

Inflation Operation How can we change the distribution of transition probabilities such that prefered neighbours are further favoured and less popular neighbours are demoted. � Idea: � MCL Solution: raise all the entries in a given column to a certain power greater than 1 (e. g. squaring) and rescaling the column to have the sum 1 again.

Example for Inflation Operation

Definition for Inflation Operation

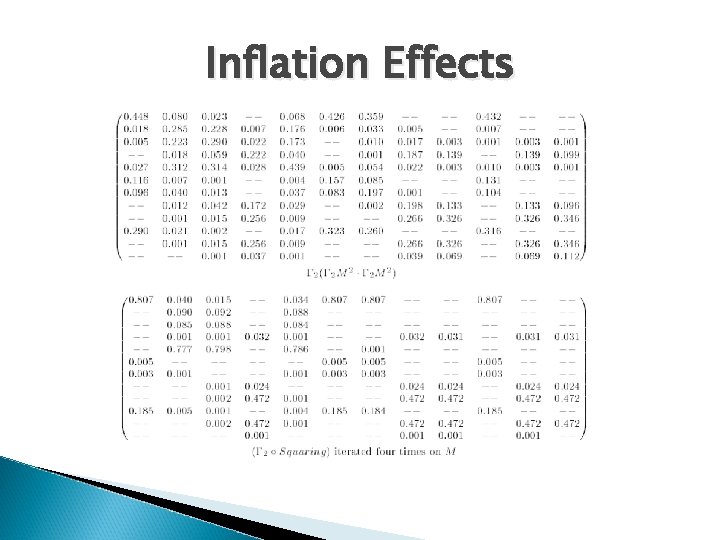
Apply Inflation Operation to the previous Markov Matrix

Inflation Effects

MCL Opeartions � Expansion Operation: power of matrix, expansion of dense region � Inflation Operation: mention aboved, elimination of unfavoured region

Markov Cluster Algorithm

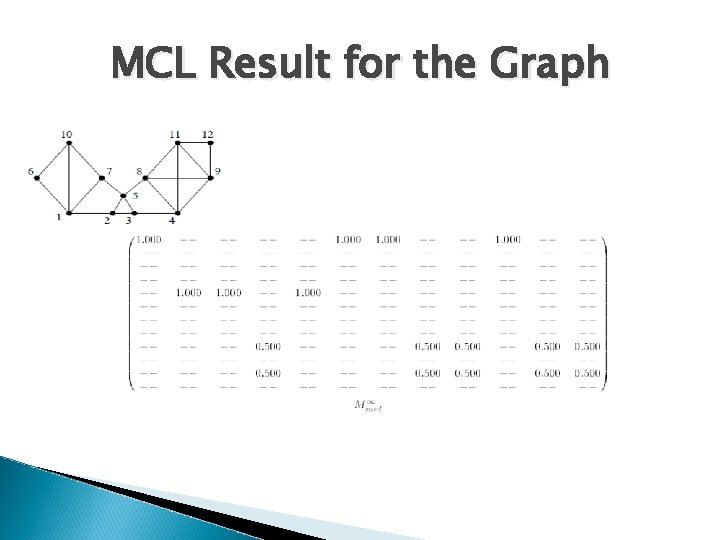
MCL Result for the Graph

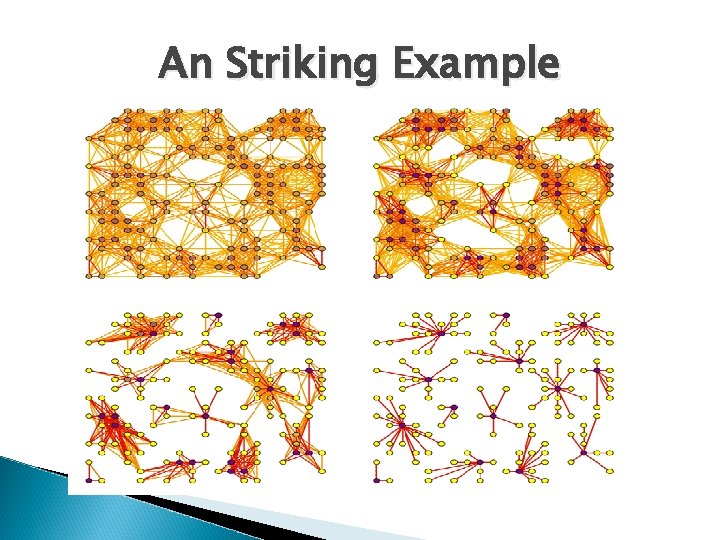
An Striking Example

Striking Animation � http: //www. micans. org/mcl/ani/mcl- animation. html

Mapping nonnegative idempotent matrces onto clusters � Find attractor: the node a is an attractor if Maa is nonzero � Find attractor system: If a is an attractor then the set of its neighbours is called an attractor system. � If there is a node who has arc connected to any node of an attractor system, the node will belong to the same cluster as that attractor system.

Example Attractor Set={1, 2, 3, 4, 5, 6, 7, 8, 9, 10} The Attractor System is {1, 2, 3}, {4, 5, 6, 7}, {8, 9}, {10} The overlaping clusters are {1, 2, 3, 11, 12, 15}, {4, 5, 6, 7, 13}, {8, 9, 12, 13, 14, 15}, {10, 12, 13}

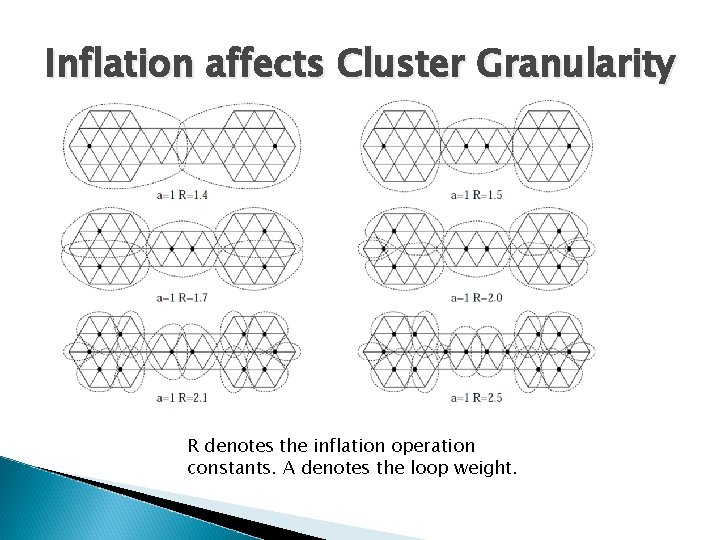
MCL Feature � how many steps are requred begore the algorithm converges to a idempoent matrix? � The number is typically somewhere between 10 and 100 � The effect of inflation on cluster granularity

Inflation affects Cluster Granularity R denotes the inflation operation constants. A denotes the loop weight.

Summary � MCL stimulates random walk on graph to find cluster � Expansion promotes dense region; while Inflation demotes the less favoured region � There is intrinsic relationship between MCL result and cluster structure

Questions And Answers