Marking scheme Without formula sheet Equations 45 Processes

Marking scheme • Without formula sheet Equations (45%) Processes (40%) Final results (10%) + units (5%) • With formula sheet Equations (15%) Processes (50%) Final results (25%) + units (10%)

22. 4 Reactions approaching equilibrium Case 1: First order reactions: A → B B → A the net rate change for A is therefore v = k[A] v = k’ [B] if [B]0 = 0, one has [A] + [B] = [A]0 at all time. the integrated solution for the above equation is [A] = As t → ∞, the concentrations reach their equilibrium values: [A]eq = [B]eq = [A]0 – [A]eq =

• The equilibrium constant can be calculated as K = thus: • In a simple way, at the equilibrium point there will be no net change and thus the forward reaction will be equal to the reverse reaction: k[A]eq = k’ [B]eq thus the above equation bridges thermodynamic quantity, chemical equilibrium, and reaction rates. • For a general reaction scheme:

22. 5 The temperature dependence of reaction rates • Arrhenius equation: A is the pre-exponential factor; Ea is the activation energy. The two quantities, A and Ea, are called Arrhenius parameters. • In an alternative expression lnk = ln. A one can see that the plot of lnk against 1/T gives a straight line.

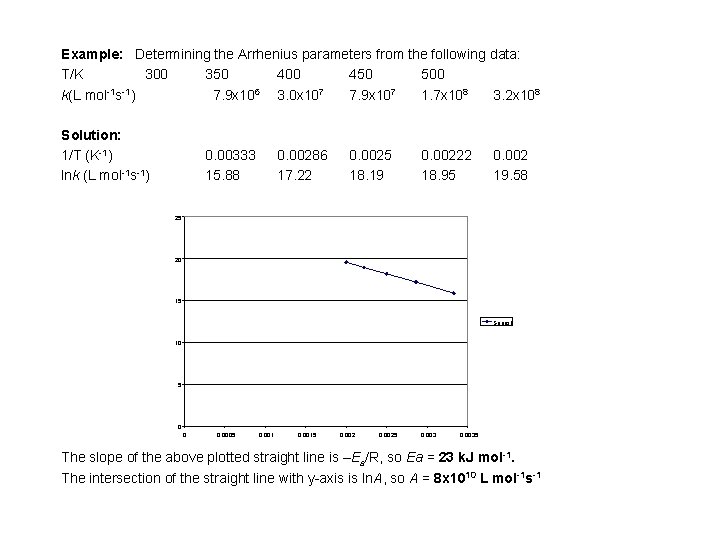
Example: Determining the Arrhenius parameters from the following data: T/K 300 350 400 450 500 k(L mol-1 s-1) 7. 9 x 106 3. 0 x 107 7. 9 x 107 1. 7 x 108 3. 2 x 108 Solution: 1/T (K-1) lnk (L mol-1 s-1) 0. 00333 15. 88 0. 00286 17. 22 0. 0025 18. 19 0. 00222 18. 95 0. 002 19. 58 25 20 15 Series 1 10 5 0 0 0. 0005 0. 0015 0. 0025 0. 0035 The slope of the above plotted straight line is –Ea/R, so Ea = 23 k. J mol-1. The intersection of the straight line with y-axis is ln. A, so A = 8 x 1010 L mol-1 s-1

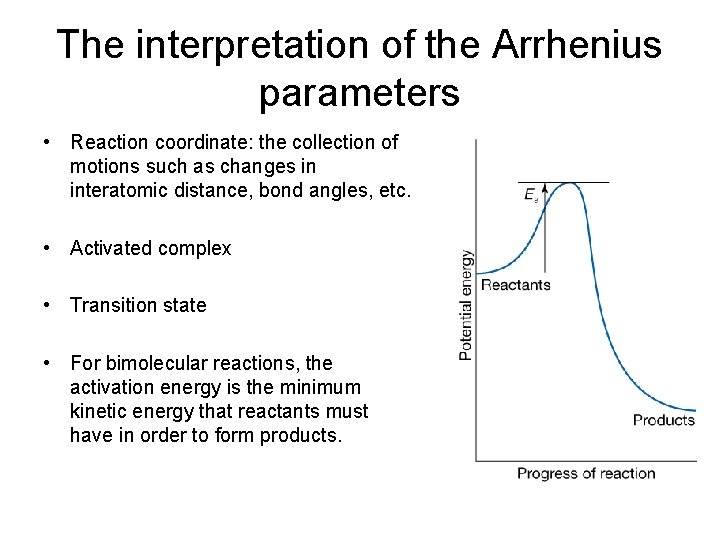
The interpretation of the Arrhenius parameters • Reaction coordinate: the collection of motions such as changes in interatomic distance, bond angles, etc. • Activated complex • Transition state • For bimolecular reactions, the activation energy is the minimum kinetic energy that reactants must have in order to form products.

Applications of the Arrhenius principle • Temperature jump-relaxation method: consider a simple first order reaction: A↔B at equilibrium: After the temperature jump the system has a new equilibrium state. Assuming the distance between the current state and the new equilibrium state is x, one gets [A] = [A]eq + x; [B] = [B]eq - x; = - (ka + kb)x Because therefore one gets dx/dt = - (ka + kb)x

Example: The H 2 O(l) ↔ H+(aq) + OH-(aq) equilibrium relaxes in 37 μs at 298 K and p. Kw = 14. 0. Calculate the rate constants for the forward and backward reactions. Solution: the net rate of ionization of H 2 O is we write [H 2 O] = [H 2 O]eq + x; and obtain: [H+] = [H+]eq – x; [OH-] = [OH-]eq – x Because x is small, k 2 x 2 can be ignored, so Because k 1[H 2 O]eq = k 2[H+]eq[OH-]eq at equilibrium condition = hence k 2 = 1. 4 x 1011 L mol-1 s-1 k 1 = 2. 4 x 10 -5 s-1 =

• Self-test 22. 5: Derive an expression for the relaxation time of a concentration when the reaction A + B ↔ C + D is second-order in both directions.

22. 6 Elementary reactions • Elementary reactions: reactions which involves only a small number of molecules or ions. A typical example: H + Br 2 → HBr + Br • Molecularity: the number of molecules coming together to react in an elementary reaction. • Molecularity and the reaction order are different !!! Reaction order is an empirical quantity, and obtained from the experimental rate law; molecularity refers to an elementary reaction proposed as an individual step in a mechanism. It must be an integral.

• An elementary bimolecular reaction has a second-order rate law: A + B → P • If the reaction is an elementary bimolecular process, then it has second-order kinetics; However, if the kinetics are second-order, then the reaction might be complex.

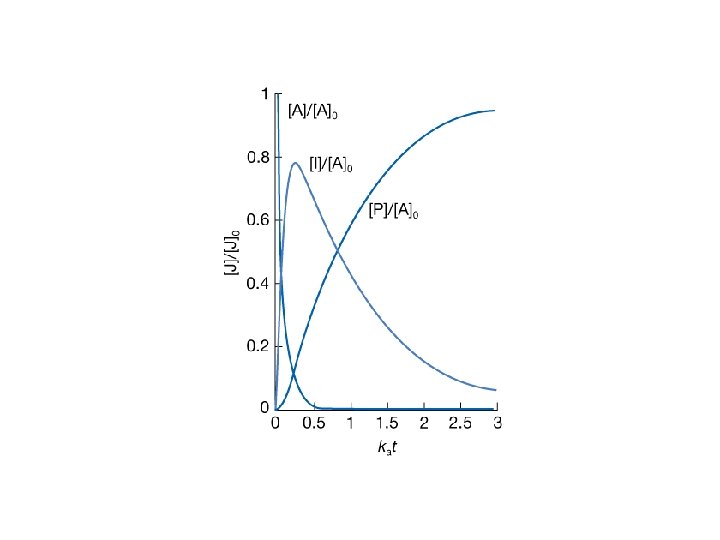
22. 7 Consecutive elementary reactions • An example: 239 U → 239 Np → 239 Pu • Consecutive unimolecular reaction A → B → C The rate of decomposition of A is: • The intermediate B is formed from A, but also decays to C. The net rate of formation of B is therefore: • The reagent C is produced from the unimolecular decay of B:

• Integrated solution for the first order reaction (A) is: • Then one gets a new expression for the reactant B: the integrated solution for the above equation is: when assuming [B] 0 = 0. • Based on the conservation law [A] + [B] + [C] = [A]0

Example. In an industrial batch process a substance A produces the desired compound B that goes on to decay to a worthless product C, each step of the reaction being first-order. At what time will B be present in the greatest concentration? Solution: At the maximum value of B Using the equation 25. 7. 6 and taking derivatives with respect to t: In order to satisfy =0 tmax = The maximum concentration of B can be calculated by plugging the tmax into the equation.

Steady State Approximation • Assuming that after an initial induction period, the rates of change of concentrations of all reaction intermediates are negligibly small. • Substitute the above expression back to the rate law of B 0≈ [B] = (k 1/ k 2)[A] • Then • The integrated solution of the above equation is [C] ≈ (1 - )[A] 0

Self-test 22. 8 Derive the rate law for the decomposition of ozone in the reaction 2 O 3(g) → 3 O 2(g) on the basis of the following mechanism O 3 → O 2 + O k 1 O 2 + O → O 3 k 1’ O + O 3 → O 2 + O 2 k 2 Solution: First write the rate law for the reactant O 3 and the intermediate product O Applying the steady state approximation to [O] Plug the above relationship back to the rate law of [O 3]