MARK MAXIMISER Express the formula for the nth

- Slides: 5

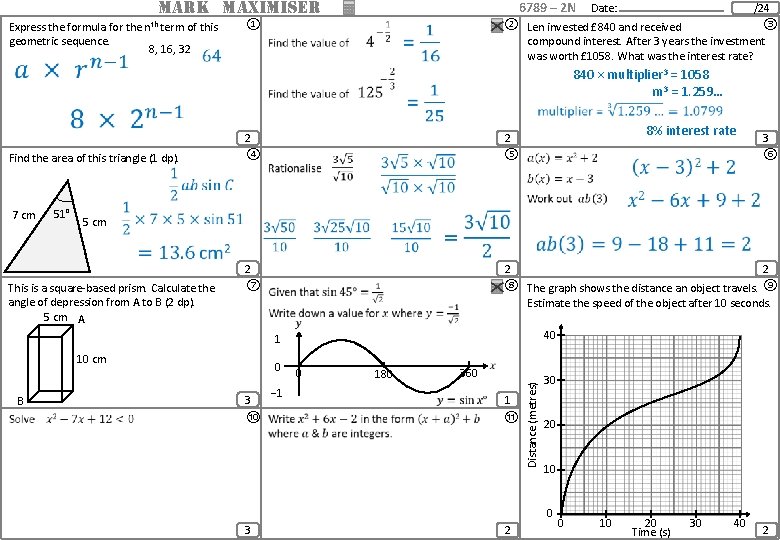
MARK MAXIMISER Express the formula for the nth term of this geometric sequence. 8, 16, 32 ① 6789 – 2 N 51° 3 ⑥ 5 cm This is a square-based prism. Calculate the angle of depression from A to B (2 dp). 5 cm A ⑦ 2 10 cm Estimate the speed of the object after 10 seconds. 0 3 ⑩ − 1 2 ⑧ The graph shows the distance an object travels. ⑨ 1 2 ⑤ 2 B ③ 0 40 360 180 1 ⑪ Distance (metres) 7 cm ② Len invested £ 840 and received compound interest. After 3 years the investment was worth £ 1058. What was the interest rate? 2 ④ /24 Find the area of this triangle (1 dp). Date: 30 20 10 0 3 2 0 10 20 Time (s) 30 40 2

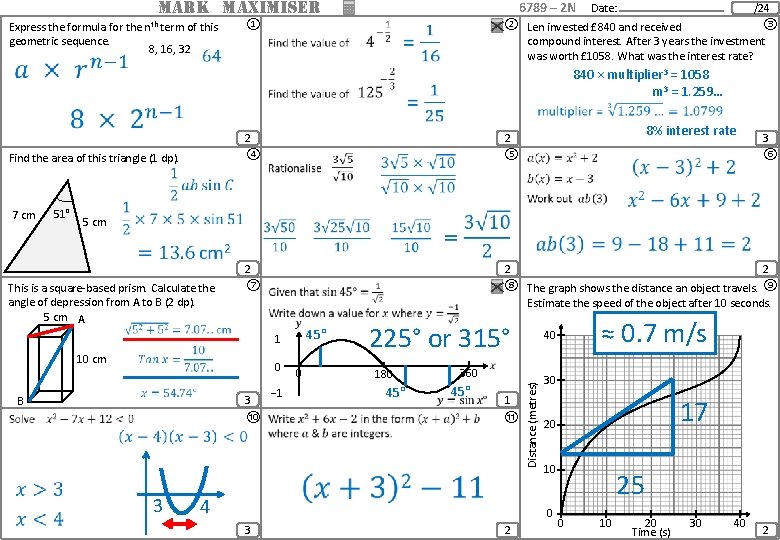
MARK MAXIMISER ① ④ 51° 5 cm This is a square-based prism. Calculate the angle of depression from A to B (2 dp). 5 cm A ⑦ 2 ⑧ The graph shows the distance an object travels. ⑨ Estimate the speed of the object after 10 seconds. − 1 0 40 360 180 1 ⑪ 30 20 10 0 3 3 ⑥ 0 ⑩ 2 10 cm 3 8% interest rate 2 1 B ⑤ ③ 840 × multiplier 3 = 1058 m 3 = 1. 259… 2 7 cm /24 compound interest. After 3 years the investment was worth £ 1058. What was the interest rate? 2 Find the area of this triangle (1 dp). Date: ② Len invested £ 840 and received Distance (metres) Express the formula for the nth term of this geometric sequence. 8, 16, 32 6789 – 2 N 2 0 10 20 Time (s) 30 40 2

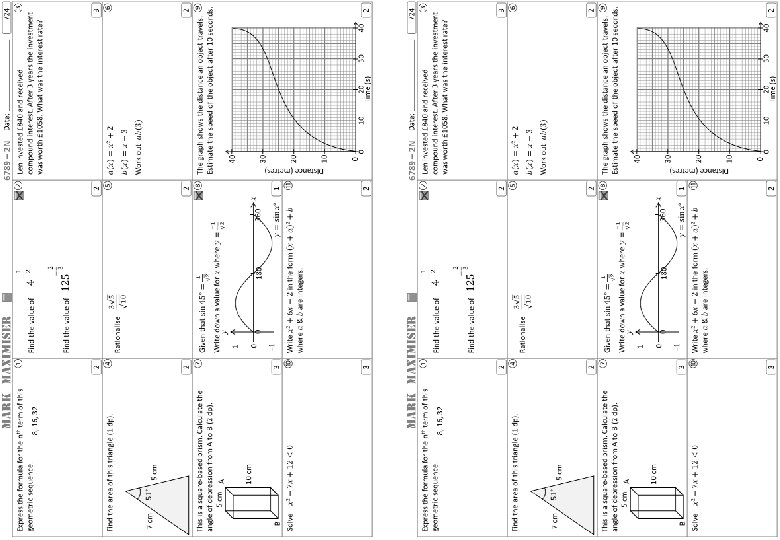
MARK MAXIMISER ① ④ 51° 5 cm ⑦ ⑩ Estimate the speed of the object after 10 seconds. 0 45° 225° or 315° 45° − 1 360 180 45° 1 ⑪ 4 30 2 17 20 10 0 3 ≈ 0. 7 m/s 40 3 2 ⑧ The graph shows the distance an object travels. ⑨ 0 3 3 ⑥ 1 2 B 8% interest rate 2 This is a square-based prism. Calculate the angle of depression from A to B (2 dp). 5 cm A 10 cm ⑤ ③ 840 × multiplier 3 = 1058 m 3 = 1. 259… 2 7 cm /24 compound interest. After 3 years the investment was worth £ 1058. What was the interest rate? 2 Find the area of this triangle (1 dp). Date: ② Len invested £ 840 and received Distance (metres) Express the formula for the nth term of this geometric sequence. 8, 16, 32 6789 – 2 N 25 0 10 20 Time (s) 30 40 2


Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk