MARK MAXIMISER A D H K M 6789

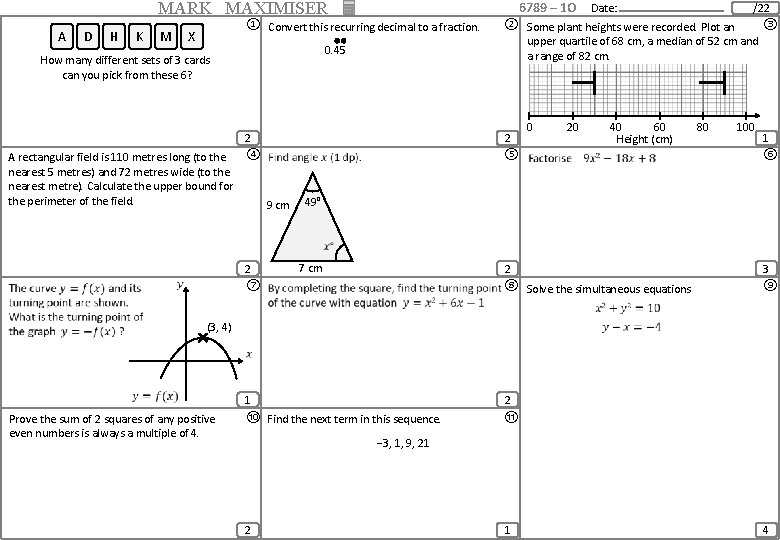
MARK MAXIMISER A D H K M 6789 – 1 O Date: ① Convert this recurring decimal to a fraction. X ② Some plant heights were recorded. Plot an 2 ④ A rectangular field is 110 metres long (to the nearest 5 metres) and 72 metres wide (to the nearest metre). Calculate the upper bound for the perimeter of the field. 9 cm ③ upper quartile of 68 cm, a median of 52 cm and a range of 82 cm. 0. 45 How many different sets of 3 cards can you pick from these 6? /22 2 0 20 40 60 Height (cm) 80 100 1 ⑤ ⑥ 2 3 ⑦ ⑧ Solve the simultaneous equations ⑨ 1 2 ⑩ Find the next term in this sequence. ⑪ 2 49° 7 cm (3, 4) Prove the sum of 2 squares of any positive even numbers is always a multiple of 4. − 3, 1, 9, 21 2 1 4

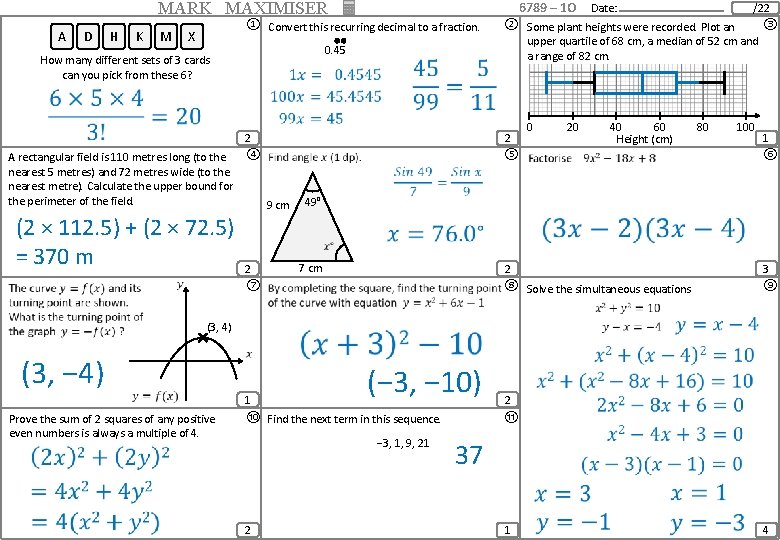
MARK MAXIMISER A D H K M 6789 – 1 O Date: ① Convert this recurring decimal to a fraction. X 2 ④ A rectangular field is 110 metres long (to the nearest 5 metres) and 72 metres wide (to the nearest metre). Calculate the upper bound for the perimeter of the field. 9 cm (2 × 112. 5) + (2 × 72. 5) = 370 m ② Some plant heights were recorded. Plot an ③ upper quartile of 68 cm, a median of 52 cm and a range of 82 cm. 0. 45 How many different sets of 3 cards can you pick from these 6? /22 2 0 20 40 60 Height (cm) 80 100 1 ⑤ ⑥ 2 3 ⑦ ⑧ Solve the simultaneous equations ⑨ 1 2 ⑩ Find the next term in this sequence. ⑪ 2 49° 7 cm (3, 4) Prove the sum of 2 squares of any positive even numbers is always a multiple of 4. − 3, 1, 9, 21 2 1 4

MARK MAXIMISER A D H K M 6789 – 1 O Date: ① Convert this recurring decimal to a fraction. X 2 ④ A rectangular field is 110 metres long (to the nearest 5 metres) and 72 metres wide (to the nearest metre). Calculate the upper bound for the perimeter of the field. 9 cm (2 × 112. 5) + (2 × 72. 5) = 370 m ② Some plant heights were recorded. Plot an 2 ③ upper quartile of 68 cm, a median of 52 cm and a range of 82 cm. 0. 45 How many different sets of 3 cards can you pick from these 6? /22 2 0 20 40 60 Height (cm) 80 100 1 ⑤ ⑥ 2 3 ⑧ Solve the simultaneous equations ⑨ 49° 7 cm ⑦ (3, 4) (3, − 4) 1 Prove the sum of 2 squares of any positive even numbers is always a multiple of 4. (− 3, − 10) ⑩ Find the next term in this sequence. − 3, 1, 9, 21 2 2 ⑪ 37 1 4

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk