MARINAWATI Studi tentang listrik dibagi atas dua bagian

MARINAWATI

Studi tentang listrik dibagi atas dua bagian, yaitu: • Listrik statik (electrostatic). Mempelajari muatan listrik yang berada dalam keadaan diam. • Listrik dinamik (electrodinamics). Mempelajari muatan listrik yang bergerak (arus listrik).

Muatan listrik dibagi dua jenis, muatan positif dan muatan negatif. Dua benda bermuatan sejenis tolak-menolak dan dua benda bermuatan tak sejenis tarik menarik. Batang kaca digosok dengan kain sutera menjadi bermuatan listrik negatif. Ketika batang kaca digosok dengan kain sutera, elektron-elektron batang kaca menuju ke kain sutera sehingga batang kaca kekurangan elektron, dan batang kaca menjadi bermuatan positif. Batang plastik digosok dengan wol menjadi bermuatan listrik positif. Ketika batang plastik digosok dengan wol, elektron wol menuju ke batang plastik sehingga batang plastik kelebihan elektron, dan batang plastik menjadi bermuatan negatif.

Hubungan gaya listrik atau gaya tolak antara dua bola bermuatan dengan jarak antara kedua muatan ditentukan oleh seorang ahli fisika bangsa Perancis bernama Charles Coulomb, pada tahun 1785. Coulomb menyimpulkan bahwa gaya tarik atau gaya tolak berbanding terbalik dengan kuadrat jarak antara kedua bola bermuatan dan gaya tarik atau gaya tolak antara dua bola bermuatan sebanding dengan muatan-muatannya. Dengan menggabung kedua kesimpulan ini, Coulomb menyatakan hukumnya yang dinamakan hukum Coulomb, yaitu: Gaya tarik atau gaya tolak antara dua muatan listrik sebanding dengan muatan-muatannya dan berbanding terbalik dengan kuadrat jarak antara kedua muatan.

F = besar gaya Coulomb (N) q 1, q 2 = muatan masing-masing partikel (coulomb, disingkat C) r = jarak pisah antara kedua muatan (m) o = permitivitas vakum atau udara = 8, 85 x 10 -12 C 2 N-1 m-2

Bila medium muatan bukan vakum atau udara maka besar gaya Coulomb antara muatan q 1 dan q 2 berkurang (Fbahan < Fudara). Jika medium memiliki permitivitas relatif r, maka tetapan 0 harus diganti dengan permitivitas bahan . = r 0

Medan listrik adalah ruang di sekitar benda bermuatan listrik di mana benda-benda bermuatan listrik lainnya dalam ruang ini akan merasakan atau mengalami gaya listrik. Medan listrik dapat digambar dengan garis-garis khayal yang dinamakan garis-garis medan (atau garis-garis gaya). Hal yang perlu diperhatikan tentang garis-garis medan: 1. Garis-garis medan tidak pernah berpotongan. 2. Garis-garis medan selalu mengarah radial ke luar menjauhi muatan positif dan radial ke dalam mendekati muatan negatif. 3. Tempat di mana garis-garis medan rapat menyatakan medan listrik yang kuat, sebaliknya tempat di mana garis-garis medan renggang menyatakan medan listrik yang lemah.

Kuat medan listrik (E) didefinisikan sebagai hasil bagi gaya Coulomb yang bekerja pada muatan uji dengan besar muatan uji tersebut (q). E = kuat medan listrik yang dihasilkan oleh muatan sumber (NC-1) F = gaya Coulomb (N) q’ = muatan uji (C) Untuk muatan uji positif, vektor gaya Coulomb F searah dengan vektor kuat medan listrik E, dan untuk muatan uji negatif, vektor gaya Coulomb F berlawanan arah dengan vektor kuat medan listrik E.

Rumus kuat medan listrik oleh sebuah muatan titik R = jarak titik terhadap muatan sumber (m) q = muatan sumber (C) E = besar kuat medan listrik (N/C)

Kuat medan listrik di suatu titik akibat beberapa muatan sumber adalah jumlah vektor (resultan) dari vektor-vektor kuat medan listrik yang dihasilkan oleh tiap muatan sumber pada titik tersebut. Ep = E 1 + E 2 + E 3 ….

Fluks listrik ialah jumlah garis medan yang menembus tegak lurus suatu bidang. Hasil kali antara kuat medan listrik E dengan luas bidang A yang tegak lurus dengan medan listrik tersebut dinamakan fluks listrik . =Ex. A = E x A cos Φ = fluks listrik (weber=W) E = kuat medan listrik (N/C) A = luas bidang yang ditembus oleh medan listrik (m 2) Θ = sudut antara E dan garis normal bidang

Hukum Gauss berbunyi: Jumlah garis medan yang menembus suatu permukaan tertutup sebanding dengan jumlah muatan listrik yang dilingkupi oleh permukaan tertutup itu. = jumlah garis medan (fluks listrik) E = kuat medan listrik pada permukaan tertutup A = luas permukaan tertutup = sudut antara vektor E dan garis normal permukaan q = muatan yang dilingkupi permukaan tertutup 0 = permitivitas udara

E = kuat medan listrik pada konduktor dua keping sejajar (N/C) s = rapat muatan keping (C/m 2 atau Cm-2) 0 = permitivitas udara = 8, 85 x 10 -12 C 2 N-1 m-2

Kuat medan listrik untuk bola konduktor berongga yang diberi muatan adalah: • Di dalam bola (r < R) E=0 • Di kulit dan di luar bola (r ≥ R) R adalah jarak titik dari pusat bola

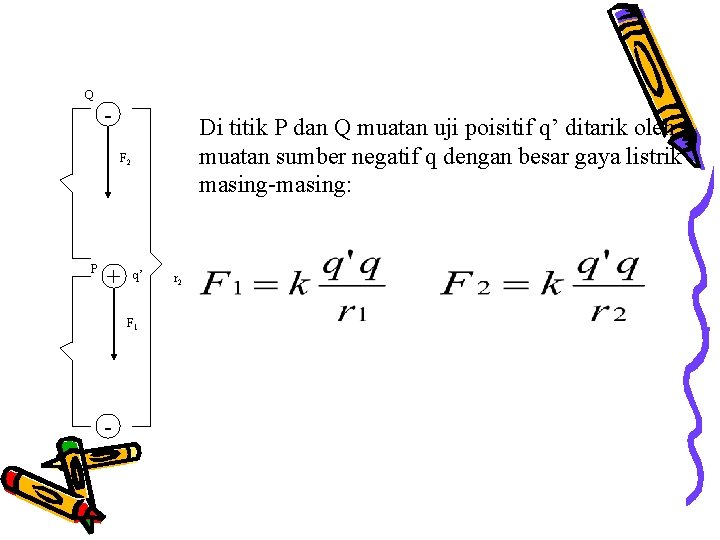
Q - Di titik P dan Q muatan uji poisitif q’ ditarik oleh muatan sumber negatif q dengan besar gaya listrik masing-masing: F 2 P + q’ F 1 - r 2

Usaha yang dilakukan sama dengan pertambahan energi potensial muatan uji q’, yaitu selisih energi potensial akhir dengan energi potensial awal: W = ∆EP =EP 2 –EP 1 ∆EP = k q’q (1/r 2 – 1/r 1) ∆EP = beda energi potensial W = Usaha yang dilakukan k = 9 x 109 Nm 2 C-2

Potensial listrik didefinisikan sebagai perubahan energi potensial per satuan muatan ketika sebuah muatan uji dipindahkan di antara dua titik.

Definisi potensial mutlak pada suatu titik yang berjarak r dari muatan q sebagai :

Potensial oleh beberapa muatan sumber. V = k q 1/r 1 + k q 2/r 2 + …. Hukum kekekalan energi mekanik dalam medan elektrostatik : Jika gesekan diabaikan dan tidak ada gaya lain yang bekerja pada partikel bermuatan kecuali gaya Couloumb, maka : EP 1 + EK 1 = EP 2 + EK 2

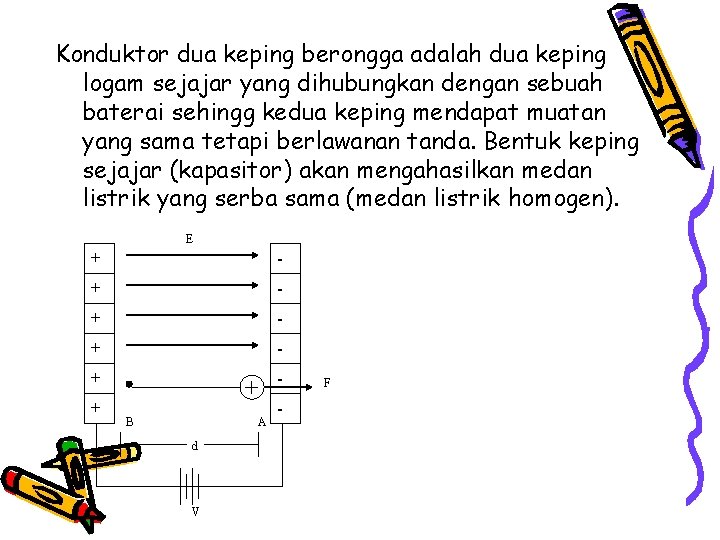
Konduktor dua keping berongga adalah dua keping logam sejajar yang dihubungkan dengan sebuah baterai sehingg kedua keping mendapat muatan yang sama tetapi berlawanan tanda. Bentuk keping sejajar (kapasitor) akan mengahasilkan medan listrik yang serba sama (medan listrik homogen). E + - + - + + + B A d V - F

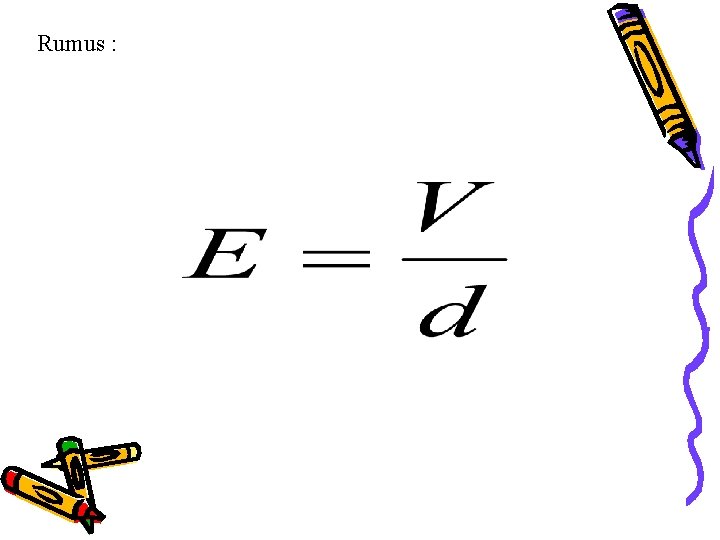
Rumus :

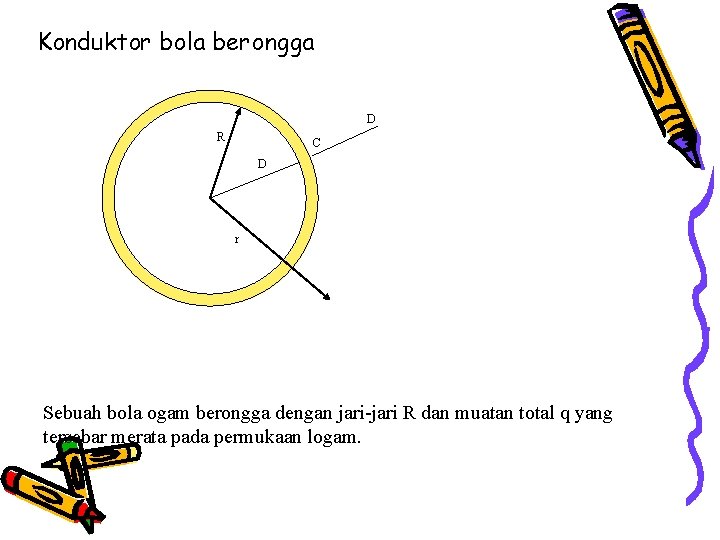
Konduktor bola berongga D R C D r Sebuah bola ogam berongga dengan jari-jari R dan muatan total q yang tersebar merata pada permukaan logam.

Kapasitor 1. Pengenalan Kapasitor adalah alat(komponen) listrik yang dibuat sedemikian rupa sehingga mampu menyimpan muatan listrik untuk sementara waktu. Pada prinsipnya sebuah kapasitor terdiri atas dua konduktor logam yg dipisahkan oleh bhn penyekat. Isolator penyekat ini sering disebut bahan dielektrik Simbol kapasitor

2. Kapasitas Kapasitor Kemampuan kapasitor menyimpan muatan dinyatakan oleh besaran kapasitas atau kapasitansi(lambang C), yg didefinisikan sebagai perbandingan tetap antara besarnya muatan q yang tersimpan dlm kapasitor dengan beda potensial V antara kedua kepingnya. dimana: q = muatan (coulomb) V =beda potensial(volt) C =kapasitas(coulomb/volt atau farad(F))

3. Kegunaan kapasitor dalam berbagai rangkaian listrik adalah: a. Mencegah loncatan bunga api listrik pada rangkaian yang mengandung kumparan, bila tiba 2 arus listrik diputuskan atau dinyalakan. b. Menyimpan muatan atau energi listrik dalam rangkaian penyala elektronik. c. Memilih panjang gelombang pada radio penerima. d. Sebagai filter dalam catu daya (power supply).

4. Bentuk Kapasitor A. Kapasitor kertas B. Kapasitor elektrolit C. Kapasitor Variabel

A. Kapasitor Kertas Kapasitor kertas memiliki: (1) plat-plat konduktor : terdiri dari dua lembar kertas timah panjang yg digulung pd sebuah silinder. (2) Bahan penyekat : terdiri dari kertas yg terdapat di antara kedua plat. (3) Besar kapasitas : 0, 1µF

B. Kapasitor Elektrolit memiliki: (1). Plat-plat konduktor : terdiri dari 2 lembar kertas aluminium. (2). Bahan penyekat : terdiri dari aluminium oksida. (3). Besar kapasitas : 105 p. F

C. Kapasitor Variabel memiliki: (1). Plat-plat konduktor : terdiri dari dua kumpulan plat 2 paralel. (2). Bahan penyekat : udara. (3). Besarnya kapasitas : bisa diubah-ubah(max 500 p. F)

5. Macam Kapasitor dan Faktor yg Mempengaruhinya a. Kapasitor keping sejajar Bila diantara kedua keping kapasitor tdk ada bhn penyekat atau bahan penyekat berupa udara, maka besar kapasitas kapasitor adalah: Dimana: C = kapasitas kapasitor keping sejajar(F) ε 0 = permitivitas hampa atau udara(8, 85. 10 -12 C 2 N-1 m-2) A = luas tiap keping (m 2) d = jarak pisah kedua keping (m)

Bila diantara kedua keping kapasitor disisipkan bahan penyekat maka besar kapasitas kapasitor adalah: dengan sehingga Dimana : K = Permitivitas relatif bahan ε = Permitivitas bahan ε 0 = Permitivitas hampa udara

Permitivitas Relatif (K) Permitivitas relatif didefinisikan sebagai perbandingan antara kapasitas dalam bahan penyekat dan kapasitas dalam vakum (udara). Secara matematis dpt dinyatakan sebagai: Dimana: K = Permitivitas relatif bahan(K>1) Cb= Kapasitas dlm bhn penyekat Co = Kapasitas dlm vakum (udara)

“Muatan kapasitor adalah kekal(muatan kapasitor sebelum disisipi bahan penyekat q 0 sama dengan muatan kapasitor setelah disisipi penyekat qb)” Secara matematis dinyatakan sebagai: Dimana: Vb = beda potensial ke 2 keping stlh disisipi bhn penyekat V 0 = beda potensial ke 2 keping sblm disisipi bhn penyekat

b. Kapasitor Bola Untuk menentukan kapasitas kapasitor bola dapat dihitung secara matematis sebagai berikut: Dengan memasukan nilai V ini kedlm pers umum kapasitor diperoleh: di mana: C = kapasitas kapasitor bola ε 0 = permitivitas udara R = jari-jari bola

6. Susunan Kapasitor A. Susunan Seri Kapasitor B. Susunan Paralel Kapasitor C. Susunan Kombinasi

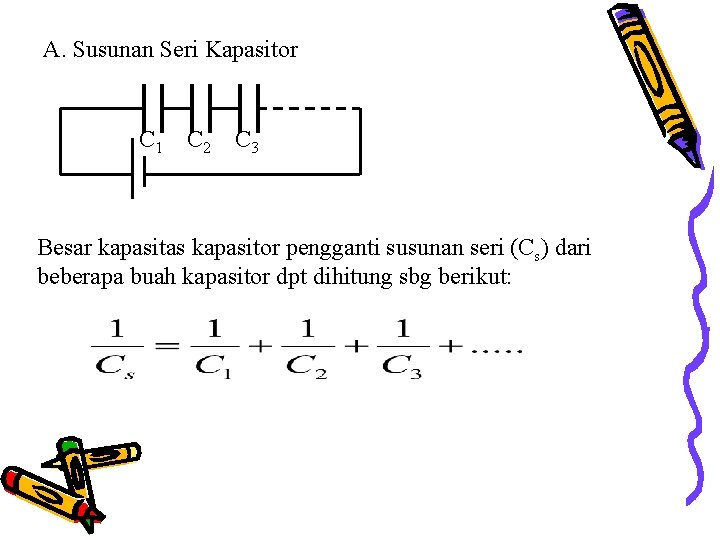
A. Susunan Seri Kapasitor C 1 C 2 C 3 Besar kapasitas kapasitor pengganti susunan seri (Cs) dari beberapa buah kapasitor dpt dihitung sbg berikut:

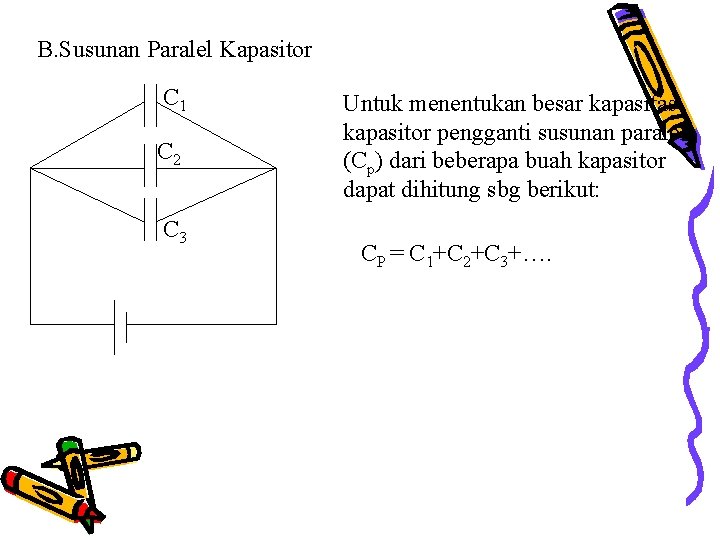
B. Susunan Paralel Kapasitor C 1 C 2 C 3 Untuk menentukan besar kapasitas kapasitor pengganti susunan paralel (Cp) dari beberapa buah kapasitor dapat dihitung sbg berikut: CP = C 1+C 2+C 3+….

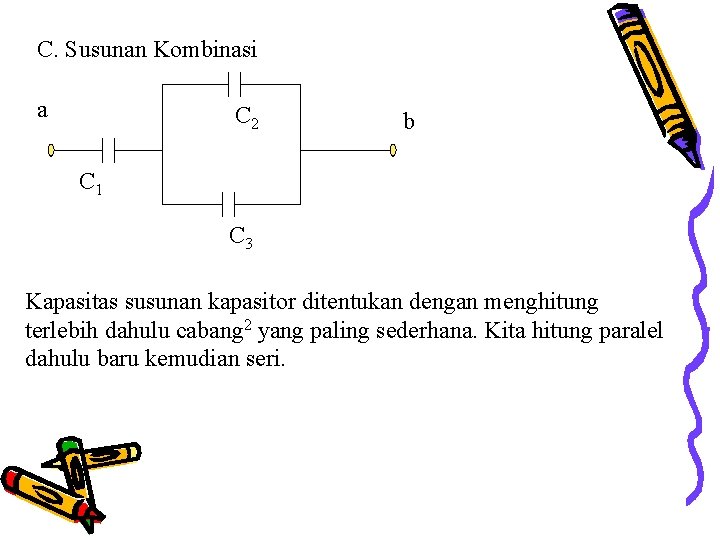
C. Susunan Kombinasi a C 2 b C 1 C 3 Kapasitas susunan kapasitor ditentukan dengan menghitung terlebih dahulu cabang 2 yang paling sederhana. Kita hitung paralel dahulu baru kemudian seri.

7. Kapasitor Gabungan Jika ada 2 buah kapasitor maka kapasitor tsb dpt digabung dgn tiga cara yaitu dengan cara: 1. Menyentuh

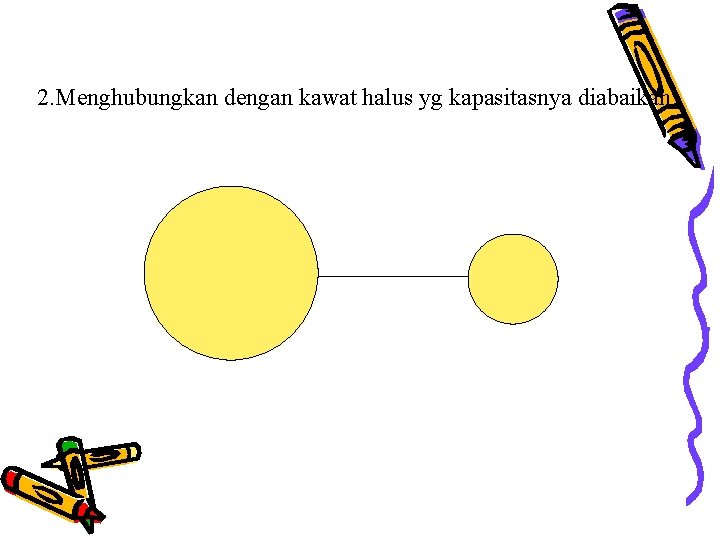
2. Menghubungkan dengan kawat halus yg kapasitasnya diabaikan

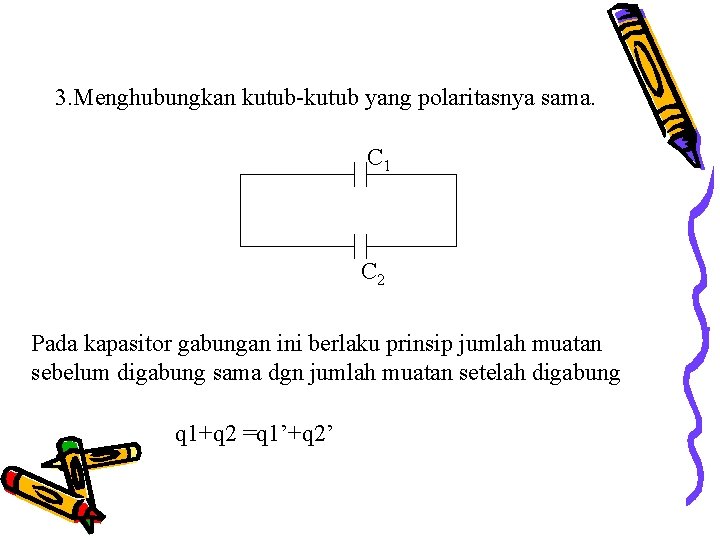
3. Menghubungkan kutub-kutub yang polaritasnya sama. C 1 C 2 Pada kapasitor gabungan ini berlaku prinsip jumlah muatan sebelum digabung sama dgn jumlah muatan setelah digabung q 1+q 2 =q 1’+q 2’

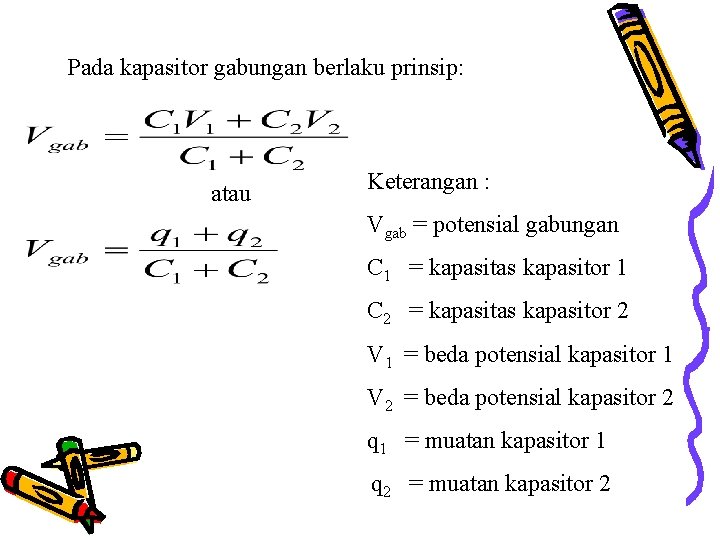
Pada kapasitor gabungan berlaku prinsip: atau Keterangan : Vgab = potensial gabungan C 1 = kapasitas kapasitor 1 C 2 = kapasitas kapasitor 2 V 1 = beda potensial kapasitor 1 V 2 = beda potensial kapasitor 2 q 1 = muatan kapasitor 1 q 2 = muatan kapasitor 2

8. Energi yang Tersimpan dalam Kapasitor Bila sebuah kapasitor diberi muatan listrik, akan terjadi perpindahan muatan dari satu keping ke keping lain. Utk perpindahan itu diperlukan usaha. Usaha yg telah dipakai utk pemindahan muatan itu akan disimpan oleh kapasitor sbg energi. Rumus beda potensial rata-rata selama proses pemindahan muatan ini adalah:

Usaha yang diperlukan utk memindahkan muatan q adalah hasil kali antara muatan yg sdh dipindahkan dgn beda potensial rata 2. Karena q = CV, maka : Oleh karena , maka :