Marginalized Kernels Graph Kernels Max Planck Institute for

Marginalized Kernels & Graph Kernels Max Planck Institute for Biological Cybernetics Koji Tsuda 1

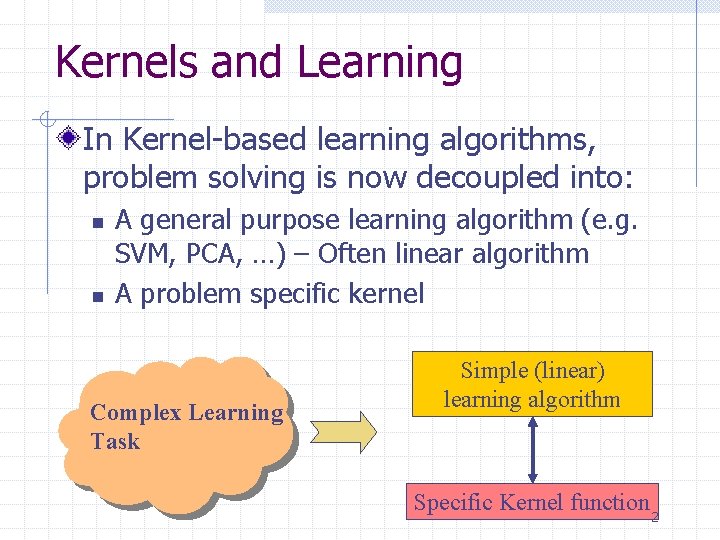
Kernels and Learning In Kernel-based learning algorithms, problem solving is now decoupled into: n n A general purpose learning algorithm (e. g. SVM, PCA, …) – Often linear algorithm A problem specific kernel Complex Learning Task Simple (linear) learning algorithm Specific Kernel function 2

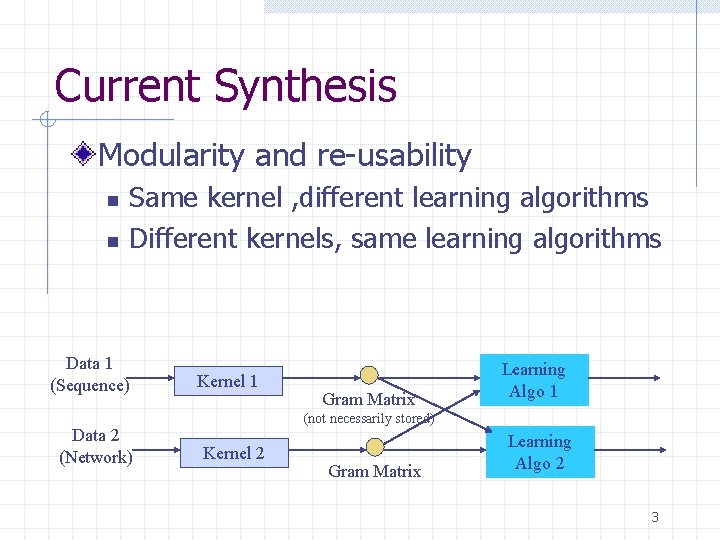
Current Synthesis Modularity and re-usability n n Same kernel , different learning algorithms Different kernels, same learning algorithms Data 1 (Sequence) Data 2 (Network) Kernel 1 Gram Matrix Learning Algo 1 (not necessarily stored) Kernel 2 Gram Matrix Learning Algo 2 3

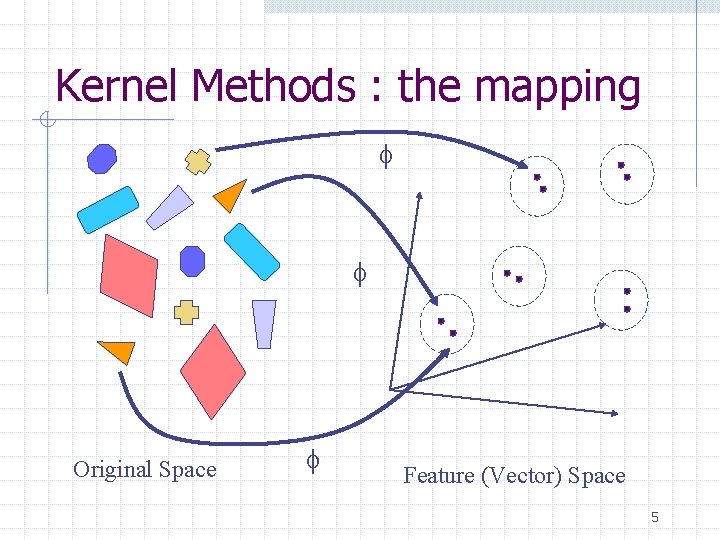
Lectures so far Kernel represents the similarity between two objects, defined as the dot-product in the feature space Various String Kernels Importance of Positive Definiteness 4

Kernel Methods : the mapping f f f Original Space Feature (Vector) Space 5

IBM Research – Tokyo Research Laboratory © 2005 IBM Corporation Overview of this lecture § Marginalized kernels – General idea about defining kernels using latent variables – An example in string kernel § Marginalized Graph Kernels – Kernel for labeled graphs (~ several hundred nodes) – Similarity for chemical compounds (drug discovery) § Diffusion Kernels – Closeness between nodes of a network – Used for function prediction of proteins based on biological networks (protein-protein interaction nets)

Marginalized kernels K. Tsuda, T. Kin, and K. Asai. Marginalized kernels for biological sequences Bioinformatics, 18(Suppl. 1): S 268 -S 275, 2002. 7

Biological Sequences: Classification Tasks DNA sequences (A, C, G, T) n Gene Finding, Splice Sites RNA sequences (A, C, G, U) n Micro. RNA discovery, Classification into Rfam families Amino Acid Sequences (20 symbols) n Remote Homolog Detection, Fold recognition 8

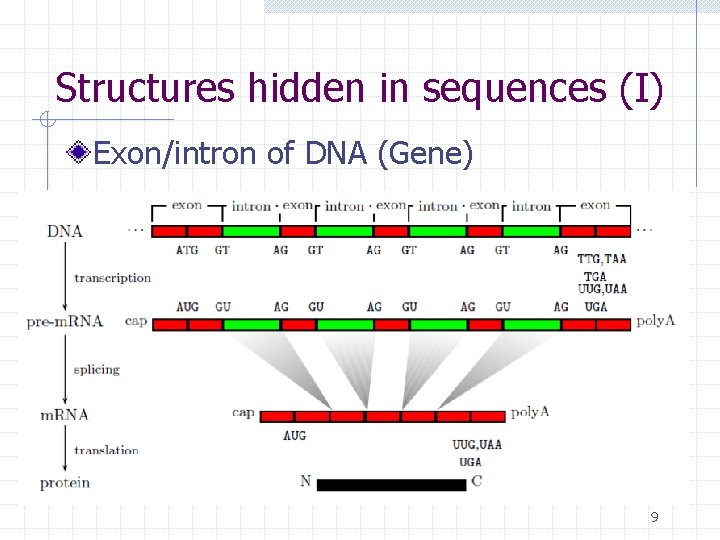
Structures hidden in sequences (I) Exon/intron of DNA (Gene) 9

Structures hidden in sequences (II) RNA Secondary Structure Protein 3 D Structures It is crucial to infer hidden structures and exploit them for classification 10

Hidden Markov Models Visible Variable Hidden Variable : Symbol Sequence : Context HMM has parameters n n Transition Probability Emission Probability HMM models the joint probability 11

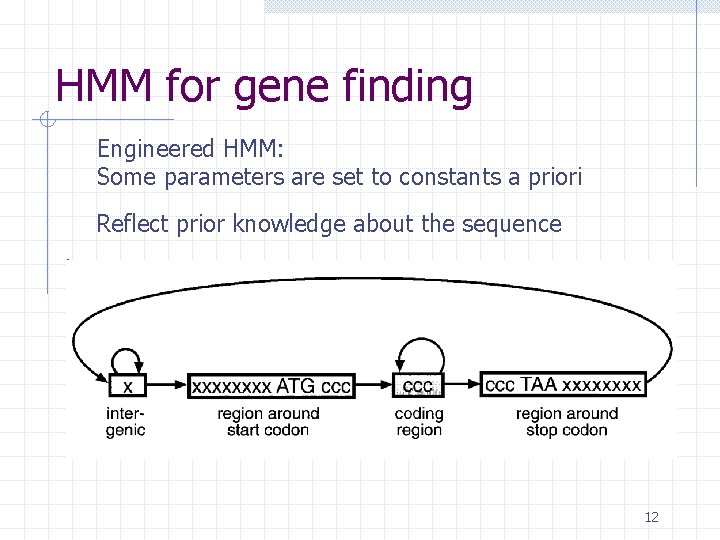
HMM for gene finding Engineered HMM: Some parameters are set to constants a priori Reflect prior knowledge about the sequence 12

Training Hidden Markov Models Training examples consist of string-context pairs n E. g. , Fragments of DNA sequences with known splice sites Parameters are estimated by the maximizing likelihood 13

Using trained hidden Markov models to estimate the context A trained HMM can compute the posterior probability Given the sequence x, what is the probability of the context h? x: A C C T G T A A A h: 1 2 2 2 2 1 1 0. 0003 h: 2 2 1 1 0. 0006 You can never predict the context perfectly! 14

Kernels for Sequences Similarity between sequences of different lengths ACGGTTCAA ATATCGCGGGAA How do you use the trained HMM for computing the kernel? 15

Count Kernel Inner product between symbol counts Extension: Spectrum kernels (Leslie et al. , 2002) n Counts the number of k-mers (k-grams) efficiently Not good for sequences with frequent context change n E. g. , coding/non-coding regions in DNA 16

Hidden Markov Models for Estimating Context Visible Variable : Symbol Sequence Hidden Variable : Context HMM can estimate the posterior probability of hidden variables from data 17

Marginalized kernels Design a joint kernel for combined n Hidden variable is not usually available n Take expectation with respect to the hidden variable The marginalized kernel for visible variables 18

Designing a joint kernel for sequences Symbols are counted separately in each context : count of a combined symbol (k, l) Joint kernel: count kernel with context information 19

Marginalization of the joint kernel Joint kernel Marginalized count kernel 20

Computing Marginalized Counts from HMM Marginalized count is described as Posterior probability of i-th hidden variable is efficiently computed by dynamic programming 21

2 nd order marginalized count kernel If adjacent relations between symbols have essential meanings, the count kernel is obviously not sufficient 2 nd order marginalized count kernel n 4 neighboring symbols (i. e. 2 visible and 2 hidden) are combined and counted 22

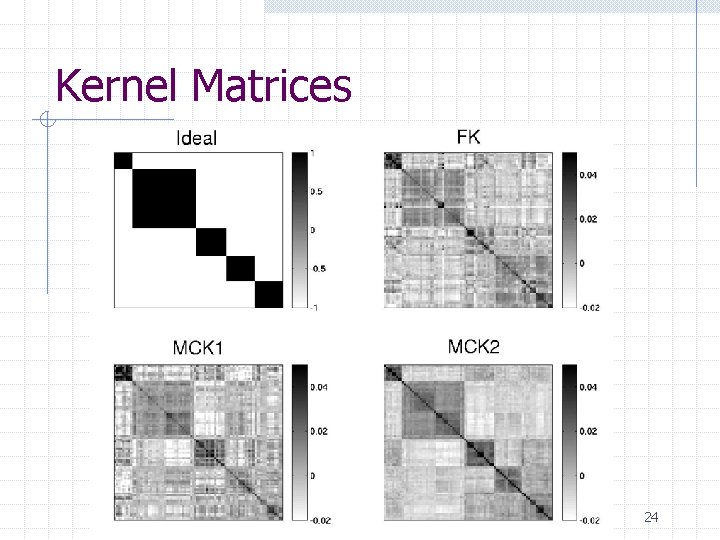
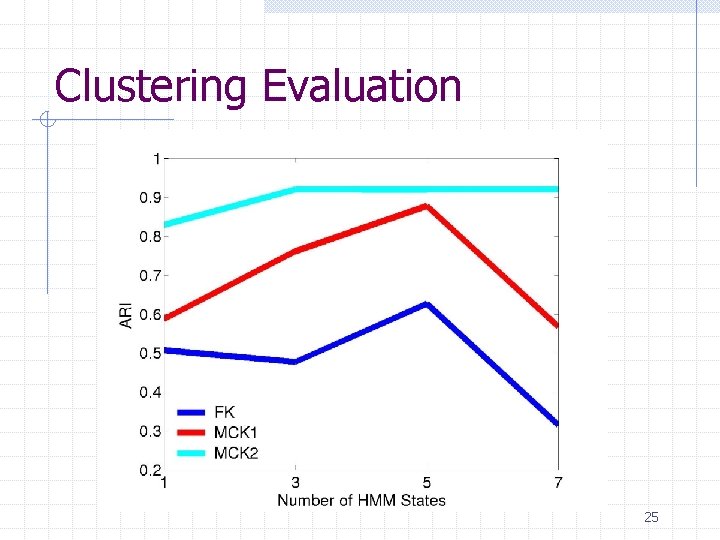
Protein clustering experiment 84 proteins containing five classes n gyr. B proteins from five bacteria species Clustering methods n HMM + {FK, MCK 1, MCK 2}+K-Means Evaluation n Adjusted Rand Index (ARI) 23

Kernel Matrices 24

Clustering Evaluation 25

Applications since then. . Marginalized Graph Kernels (Kashima et al. , ICML 2003) Sensor networks (Nyugen et al. , ICML 2004) Labeling of structured data (Kashima et al. , ICML 2004) Robotics (Shimosaka et al. , ICRA 2005) Kernels for Promoter Regions (Vert et al. , NIPS 2005) Web data (Zhao et al. , WWW 2006) Multiple Instance Learning (Kwok et al. , IJCAI 2007) 26

Summary (Marginalized Kernels) General Framework for using generative model for defining kernels Fisher kernel as a special case Broad applications Combination with CRFs and other advanced stuff? 27

2. Marginalized Graph Kernels H. Kashima, K. Tsuda, and A. Inokuchi. Marginalized kernels between labeled graphs. ICML 2003, pages 321 -328, 2003. 28

Motivations for graph analysis Existing methods assume ” tables” Serial Num 0001 0002 Name ○○ ×× Age 40 31 Sex Male Female Address Tokyo Osaka … … … Structured data beyond this framework → New methods for analysis 29

Graphs. . 30

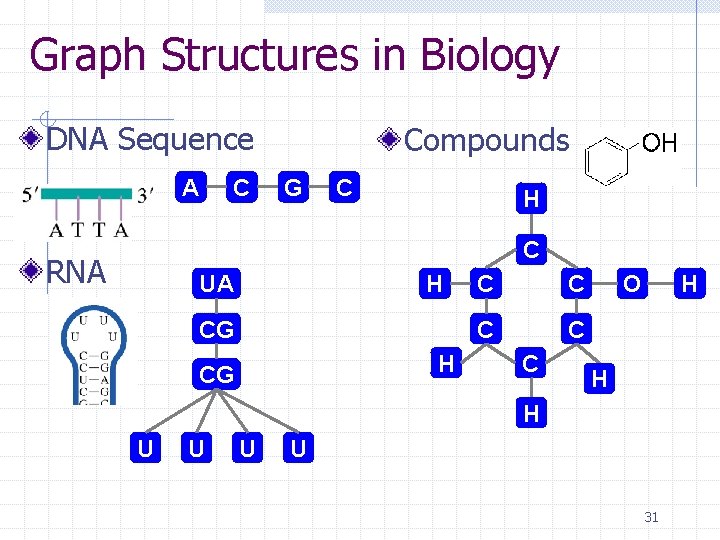
Graph Structures in Biology DNA Sequence A C Compounds G C H C RNA UA H CG C C C H O H H U U 31

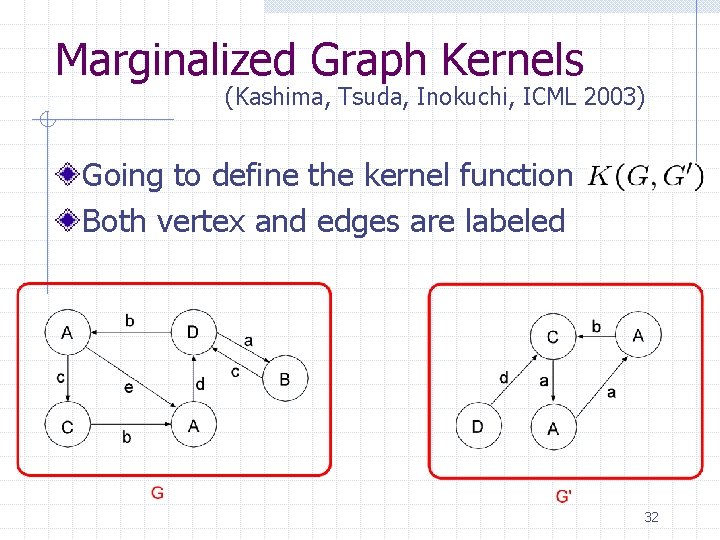
Marginalized Graph Kernels (Kashima, Tsuda, Inokuchi, ICML 2003) Going to define the kernel function Both vertex and edges are labeled 32

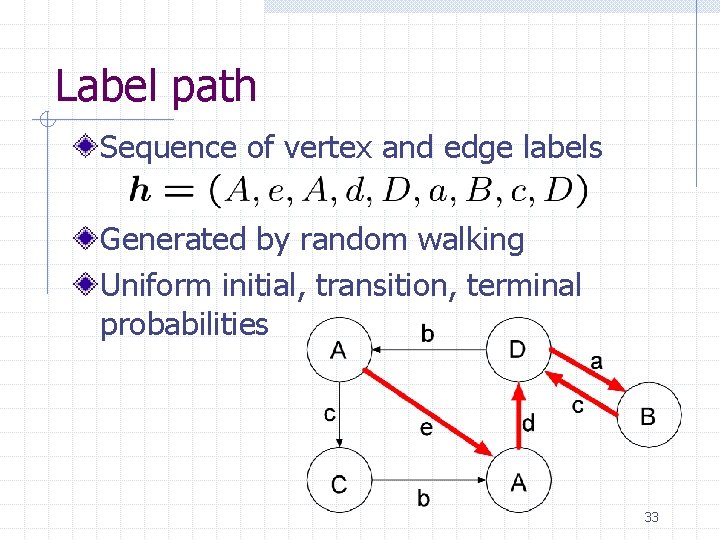
Label path Sequence of vertex and edge labels Generated by random walking Uniform initial, transition, terminal probabilities 33

Path-probability vector 34

Kernel definition Kernels for paths A c D b E B c D a A Take expectation over all possible paths! Marginalized kernels for graphs 35

Computation Transition probability : Initial and terminal : omitted n : Set of paths ending at v KV : Kernel computed from the paths ending at (v, v’) n KV is written recursively n n A(v’) Kernel computed by solving linear equations （polynomial time） v A(v) v’ 36

Graph Kernel Applications Chemical Compounds (Mahe et al. , 2005) Protein 3 D structures (Borgwardt et al, 2005) RNA graphs (Karklin et al. , 2005) Pedestrian detection Signal Processing 37

Predicting Mutagenicity MUTAG benchmark dataset n n n Mutation of Salmonella typhimurium 125 positive data (effective for mutations) 63 negative data (not effective for mutations) Mahe et al. J. Chem. Inf. Model. , 2005 38

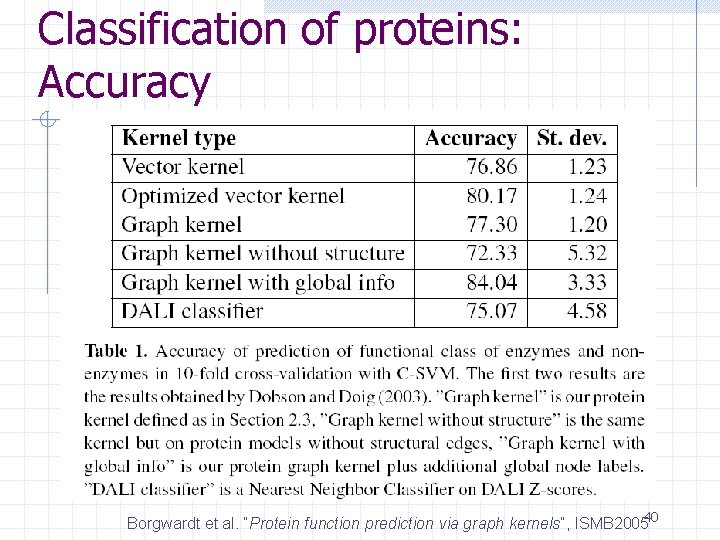
Classification of Protein 3 D structures Graphs for protein 3 D structures n n Node: Secondary structure elements Edge: Distance of two elements Calculate the similarity by graph kernels Borgwardt et al. “Protein function prediction via graph kernels”, ISMB 200539

Classification of proteins: Accuracy Borgwardt et al. “Protein function prediction via graph kernels”, ISMB 200540

Pedestrian detection in images (F. Suard et al. , 2005) 41

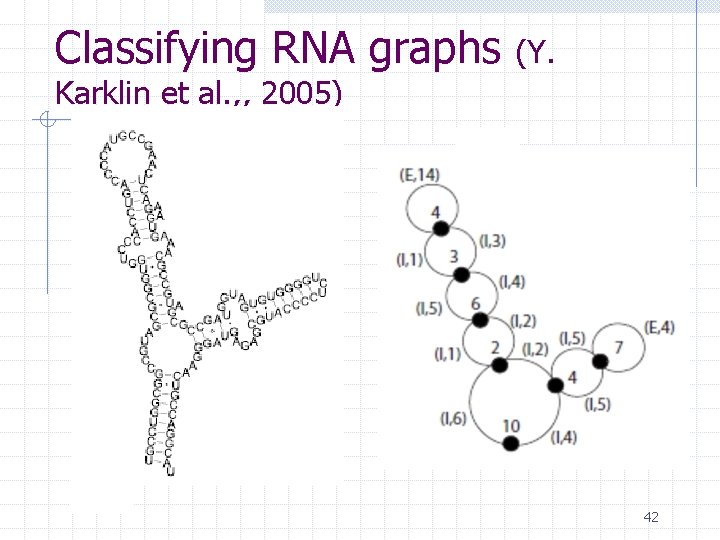
Classifying RNA graphs (Y. Karklin et al. , , 2005) 42

Strong points of MGK Polynomial time computation O(n^3) Positive definite kernel n n Support Vector Machines Kernel PCA Kernel CCA And so on… 43

Diffusion Kernels: Biological Network Analysis 44

Biological Networks • • Protein-protein physical interaction Metabolic networks Gene regulatory networks Network induced from sequence similarity • Thousands of nodes (genes/proteins) • 100000 s of edges (interactions) 45

Physical Interaction Network 46

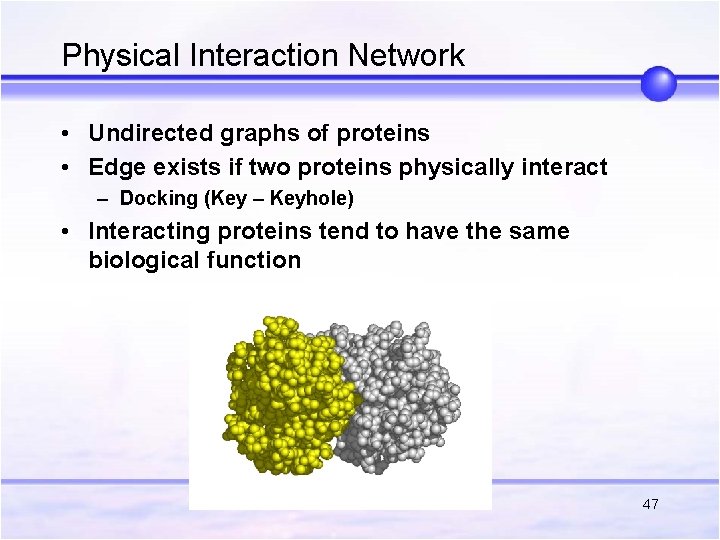
Physical Interaction Network • Undirected graphs of proteins • Edge exists if two proteins physically interact – Docking (Key – Keyhole) • Interacting proteins tend to have the same biological function 47

Metabolic Network 48

Metabolic Network • Node: Chemical compounds • Edge: Enzyme catalyzing the reaction (EC Number) Fumarate Oxaloacetate (S)-Malate 4. 2. 1. 2 1. 1. 1. 37 • KEGG Database (Kyoto University) • Collection of pathways (subnetworks) • Can be converted as a network of enzymes (proteins) 49

Protein Function Prediction • For some proteins, their functions are known • But still functions of many proteins are unknown 50

Function Prediction Using a Network • Determination of protein’s function is a central goal of molecular biology • It has to be determined by biological experiments, but accurate computational prediction helps • Proteins close to each other in the networks tend to share the same functional category • Use the network for function prediction! • (Combination with other information sources) 51

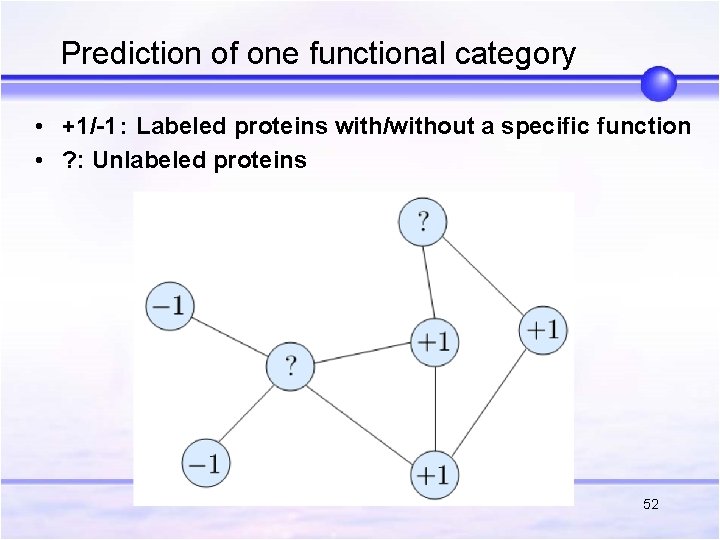
Prediction of one functional category • +1/-1： Labeled proteins with/without a specific function • ? : Unlabeled proteins 52

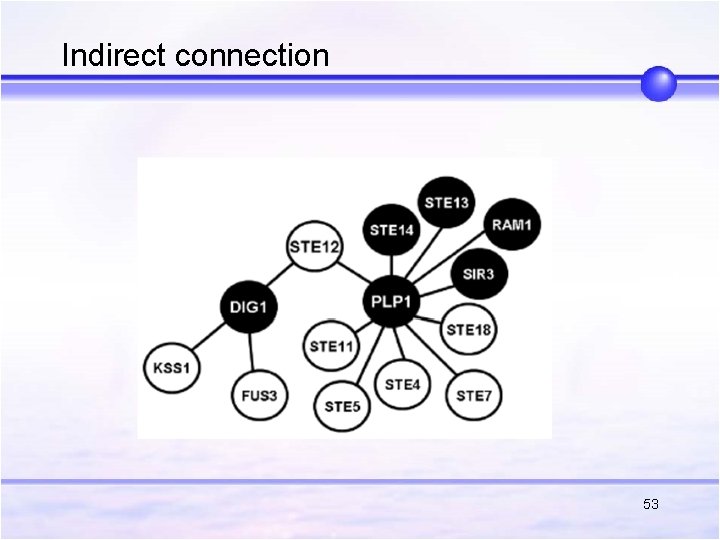
Indirect connection 53

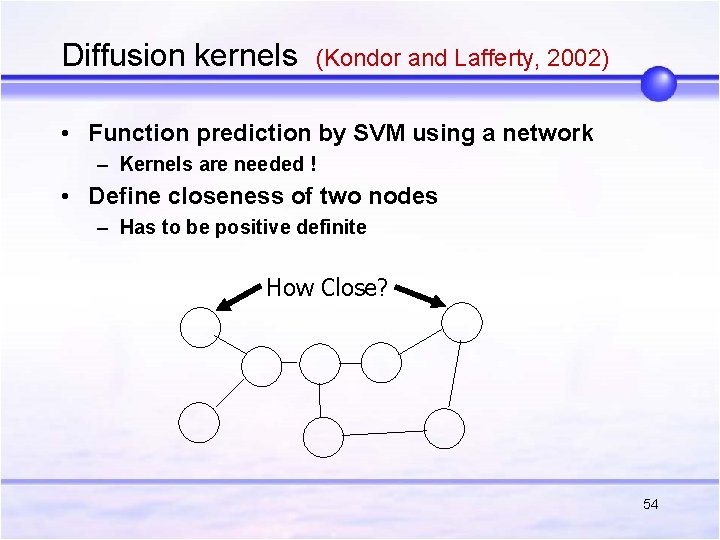
Diffusion kernels (Kondor and Lafferty, 2002) • Function prediction by SVM using a network – Kernels are needed ! • Define closeness of two nodes – Has to be positive definite How Close? 54

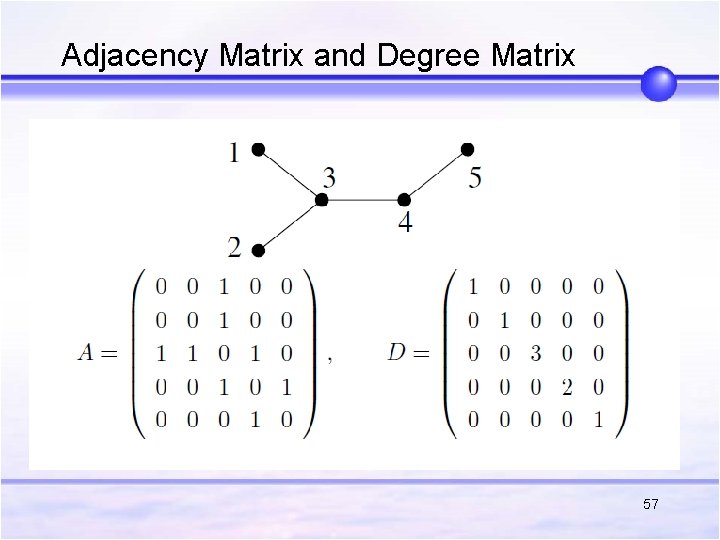
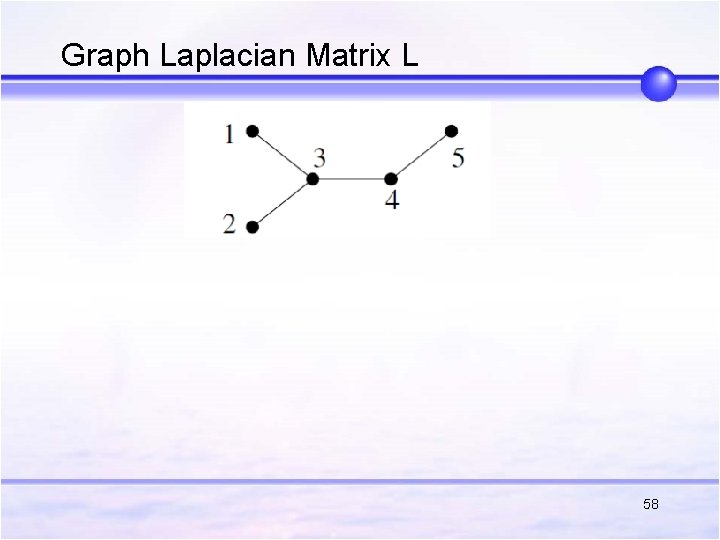
Definition of Diffusion Kernel • • A: Adjacency matrix, 　 D: Diagonal matrix of Degrees L = D-A: Graph Laplacian Matrix Diffusion kernel matrix – ：Diffusion paramater • Matrix exponential, not elementwise exponential 55

Computation of Matrix Exponential • Definition • Eigen-decomposition 56

Adjacency Matrix and Degree Matrix 57

Graph Laplacian Matrix L 58

Actual Values of Diffusion Kernels Closeness from the “central node” 59

Interpretation: Stochastic Process • For each node , consider random variable • Initial condition – Zero mean, Variance – Independent to each other (covariance zero). • Each variable sends a fraction to the neighbors 60

Stochastic Process (2) • Time Evolution Operator • Covariance • Reduce the time step 1 to • Diffusion parameter • Taking the limit 61

Interpretation via random walking • Random walking according to transition probability • Transition probability is constant • Remaining probability = Self loop • is equal to the probability of the walk that started at i being at j after infinite time steps 62

Experimental Results by Lee et al. (2006) • Yeast Proteins • 34 functional categories – Decomposed into binary classification problems • Physical Interaction Network only • Methods – Markov Random Field – Kernel Logistic Regression (Diffusion Kernel) • Use additional knowledge of correlated functions – Support Vector Machine (Diffusion Kernel) • ROC score – Higher is better 63

Experimental results by Lee et al. (2006) 64

Concluding Remarks Kernel methods have been applied to many different objects n n n Marginalized Kernels: Latent variables Marginalized Graph Kernels: Graphs Diffusion Kernels: Networks Still active field n n Mining and Learning with Graphs (MLG) Workshop Series Journal of Machine Learning Research Special Issue on Graphs (Paper due: 10. 2. 2008) THANK YOU VERY MUCH!! 65