Map skills Latitude and Longitude Types of Maps











- Slides: 25

Map skills Latitude and Longitude

Types of Maps: � Physical � Special Purpose � Political

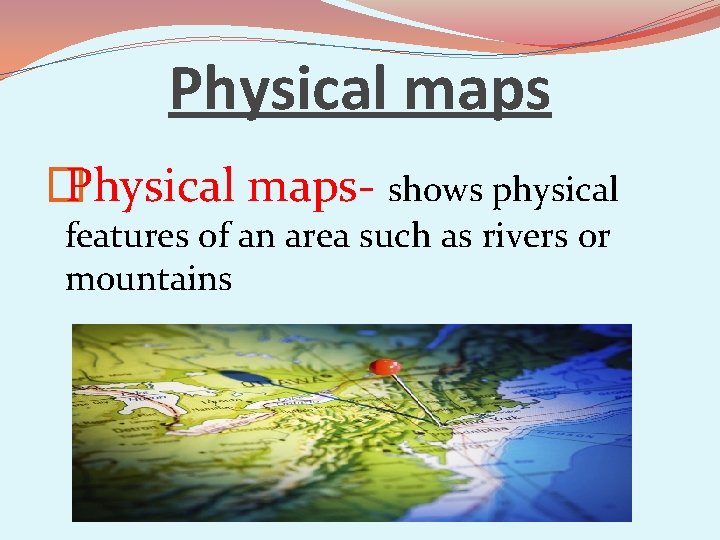
Physical maps � Physical maps- shows physical features of an area such as rivers or mountains

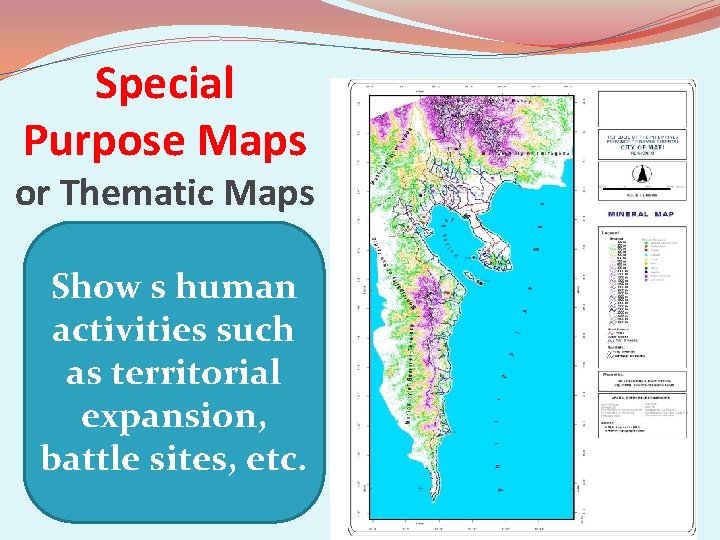
Special Purpose Maps or Thematic Maps Show s human activities such as territorial expansion, battle sites, etc.

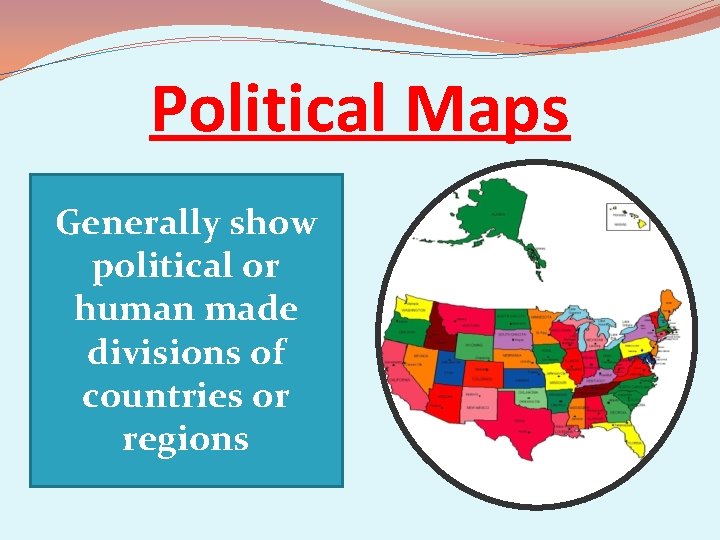
Political Maps Generally show political or human made divisions of countries or regions

Map Symbols: � Compass rose � Legend � Scale

Compass Rose (#8) A device printed on a map or chart showing the points of the compass measured from true magnetic north.

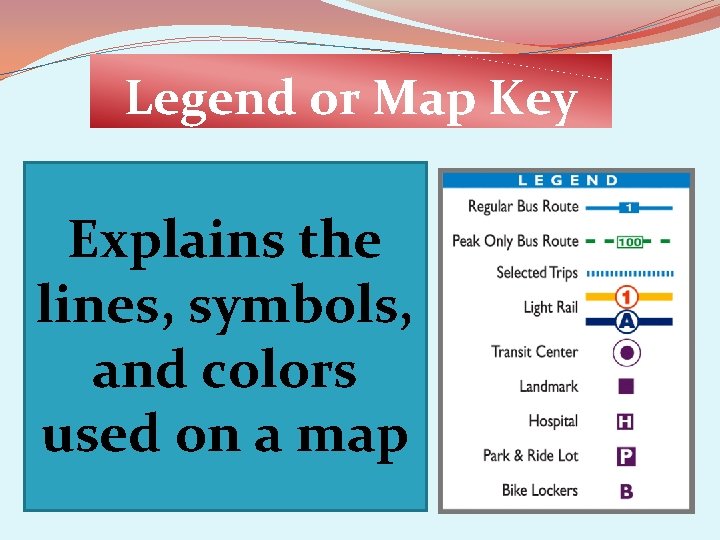
Legend or Map Key Explains the lines, symbols, and colors used on a map

Scale – often called scale bar. �A measuring line helps determine the distance on a map.

Latitude and Longitude: �Helps to locate absolute location (#7) �An exact point on Earth (described by global coordinates). - Reading and plotting points of latitude and longitude is similar to plotting and reading points on a coordinate plane.

In order to understand latitude lines you must first learn about the equator.

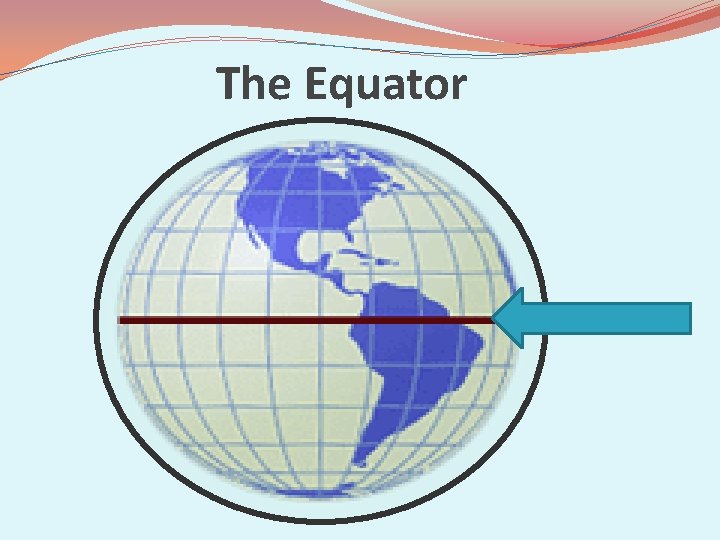
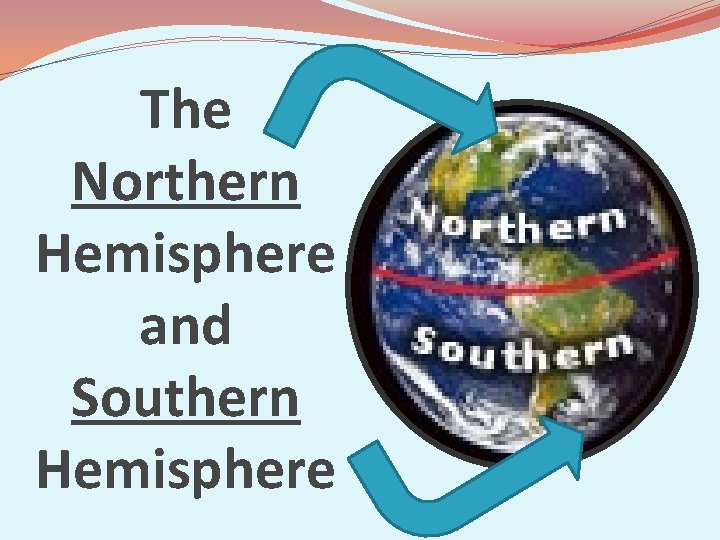
Equator (#3) �Circles the Earth at it’s mid section (like a belt). �Measures Zero degrees ( 0⁰ ). �Cuts the Earth into northern hemisphere and southern hemisphere.

The Equator

The Northern Hemisphere and Southern Hemisphere

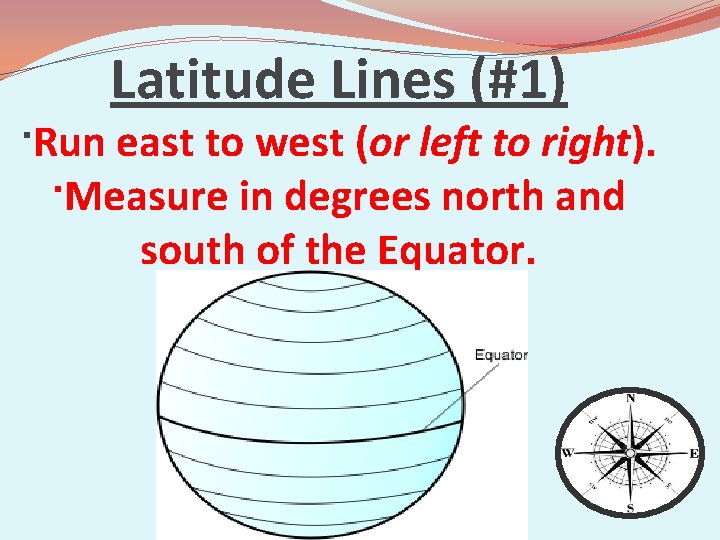
Latitude Lines (#1) ·Run east to west (or left to right). ·Measure in degrees north and south of the Equator.

Latitude lines measure in degrees from the Equator. Starting at the equator: travel “up, ” degrees increase and are north (N) Starting at the equator : travel “down, ” the degrees increase and are south (S) Latitude lines are also called parallels (#6)

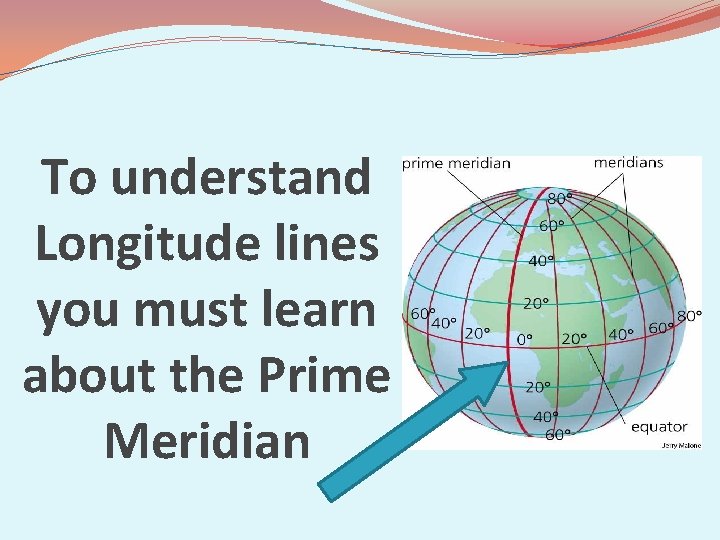
To understand Longitude lines you must learn about the Prime Meridian

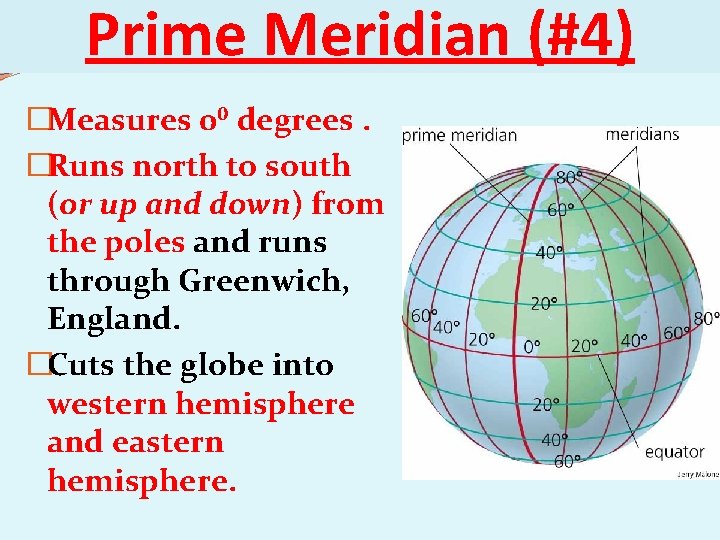
Prime Meridian (#4) �Measures 0⁰ degrees. �Runs north to south (or up and down) from the poles and runs through Greenwich, England. �Cuts the globe into western hemisphere and eastern hemisphere.

Longitude lines measure east and west of the Prime Meridian (#2) Longitude lines Are also called meridians (#5)

Lines of Longitude (Meridians) • Starting at the Prime Meridian: Travel to the left, the number of degrees increase and are WEST. • Starting at the Prime Meridian : Travel to the right, the number of degrees increase and are EAST.

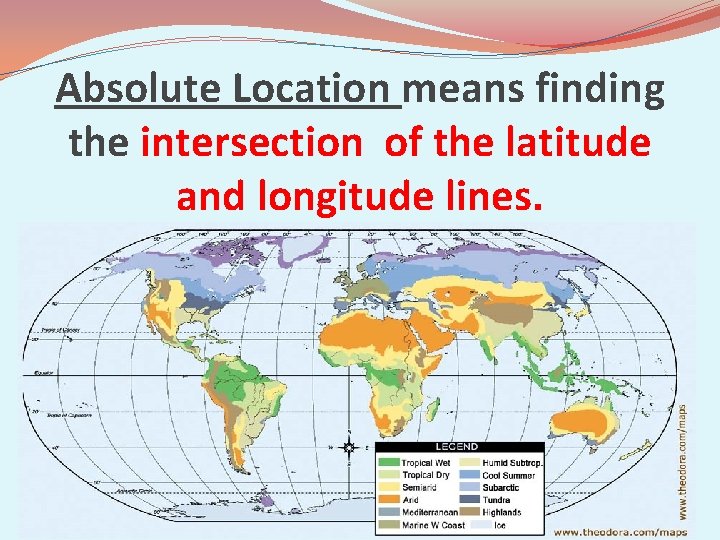
By using latitude and longitude lines, we can find Absolute Location!!! Which is the exact place somewhere is on the earth.

Absolute Location means finding the intersection of the latitude and longitude lines.

Let’s find Purcellville!

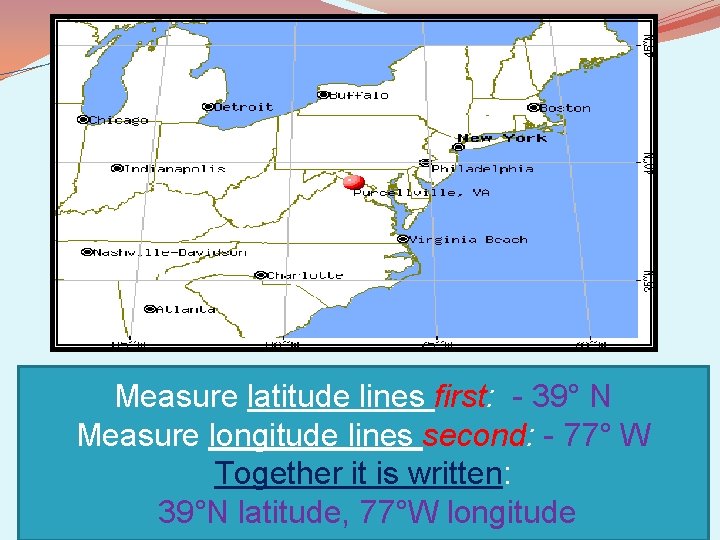
Measure latitude lines first: - 39° N Measure longitude lines second: - 77° W Together it is written: 39°N latitude, 77°W longitude

How accurate was I? ? ? �I said it was: 39°N latitude, 77°W longitude �The exact coordinate is: 39° 8' 12" N / 77° 42' 53" W �’ = minutes (1. 15 miles) �” = seconds (approx. 100 ft)