Map Projections and Coordinate Systems Gerry Daumiller Montana

Map Projections and Coordinate Systems Gerry Daumiller Montana State Library Natural Resource Information System

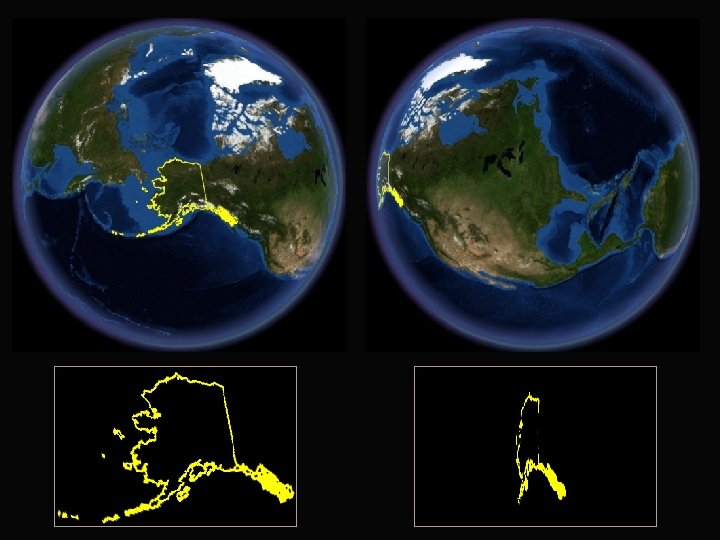
Map Projections Why are they important? An important thing to remember about map projections is that you can not generally measure distances and areas accurately from projected data. The next slides show some examples of this.

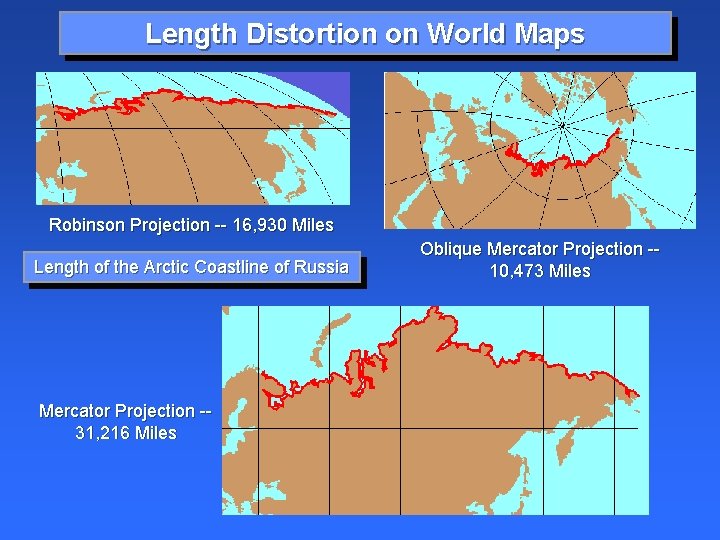
Length Distortion on World Maps Robinson Projection -- 16, 930 Miles Length of the Arctic Coastline of Russia Mercator Projection -31, 216 Miles Oblique Mercator Projection -10, 473 Miles

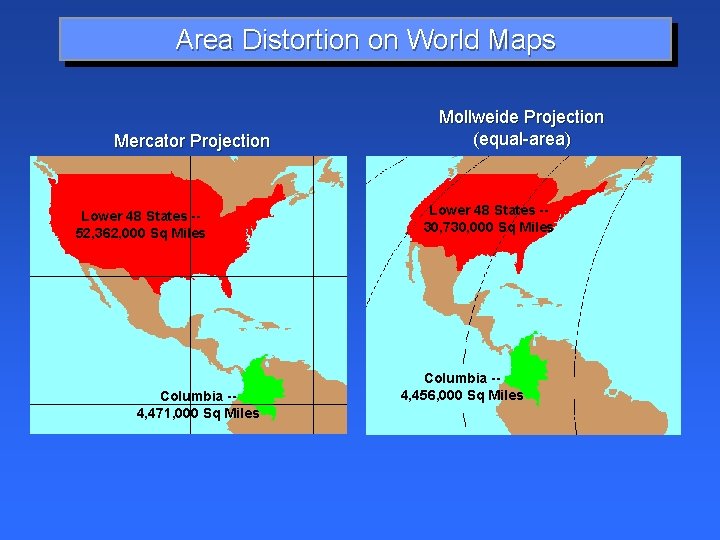
Area Distortion on World Maps Mercator Projection Lower 48 States -52, 362, 000 Sq Miles Columbia -4, 471, 000 Sq Miles Mollweide Projection (equal-area) Lower 48 States -30, 730, 000 Sq Miles Columbia -4, 456, 000 Sq Miles

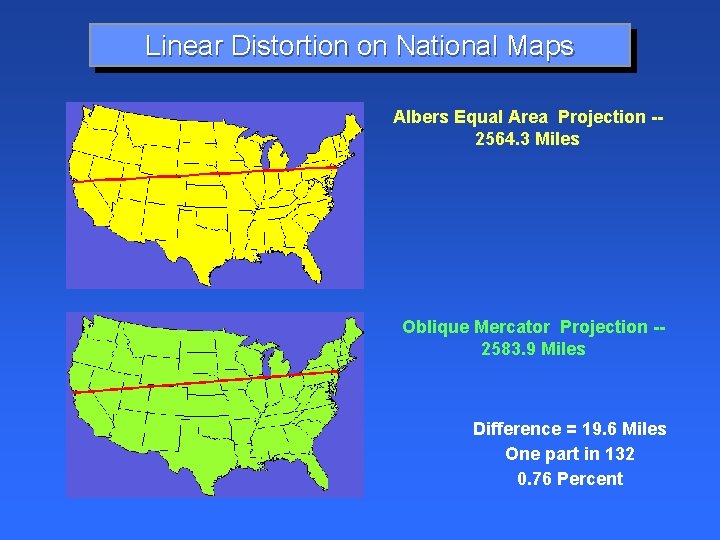
Linear Distortion on National Maps Albers Equal Area Projection -2564. 3 Miles Oblique Mercator Projection -2583. 9 Miles Difference = 19. 6 Miles One part in 132 0. 76 Percent

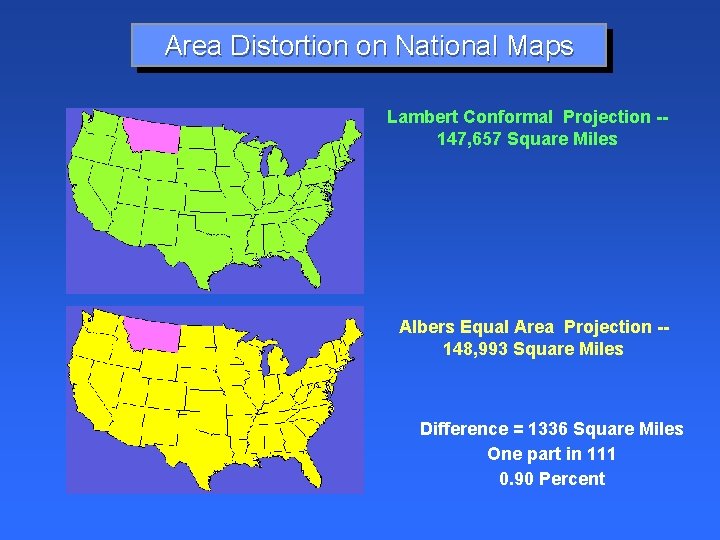
Area Distortion on National Maps Lambert Conformal Projection -147, 657 Square Miles Albers Equal Area Projection -148, 993 Square Miles Difference = 1336 Square Miles One part in 111 0. 90 Percent

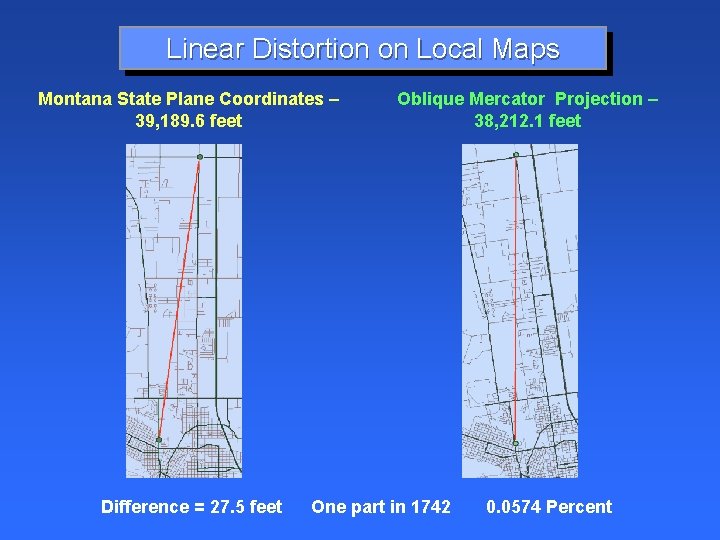
Linear Distortion on Local Maps Montana State Plane Coordinates – 39, 189. 6 feet Difference = 27. 5 feet Oblique Mercator Projection – 38, 212. 1 feet One part in 1742 0. 0574 Percent

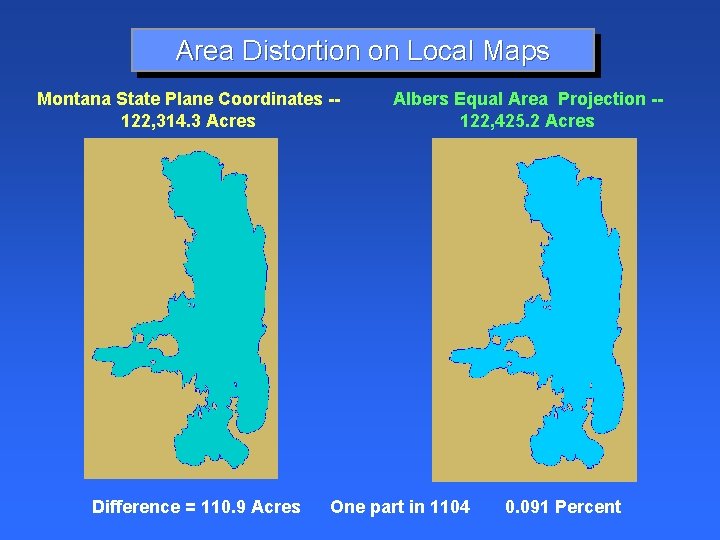
Area Distortion on Local Maps Montana State Plane Coordinates -122, 314. 3 Acres Difference = 110. 9 Acres Albers Equal Area Projection -122, 425. 2 Acres One part in 1104 0. 091 Percent

Coordinate Systems vs. Map Projections • A map projection is a method or a type of equation used to transform three-dimensional coordinates on the earth to two-dimensional coordinates on the map. • A coordinate system usually includes the specification of a map projection, plus the three dimensional model of the Earth to be used, the distance units to be used on the map, and information about the relative positions of the two dimensional map and the model of the Earth.

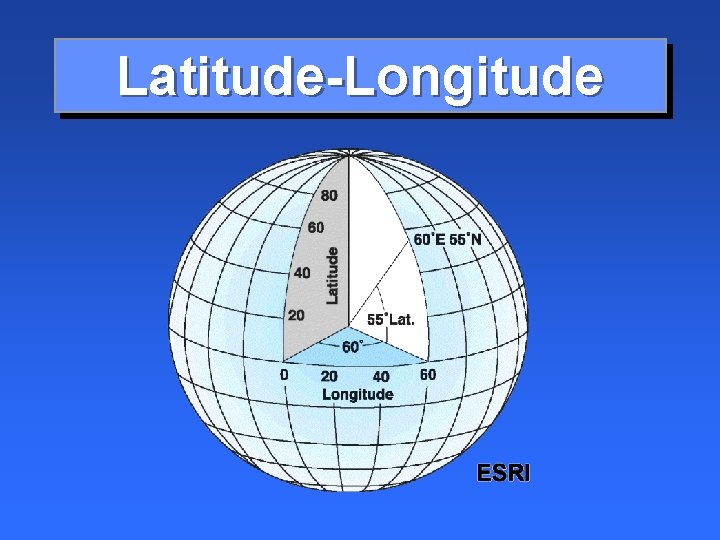
Latitude-Longitude

Latitude-Longitude • Not uniform units of measure • Meridians converge at the Poles 1° longitude at Equator = 111 km at 60° lat. = 55. 8 km at 90° lat. = 0 km 1° latitude at Equator = 111 km at 90° lat. = 112 km

Using Geographic Coordinates as Plane Coordinates Geographic Coordinates Projected Coordinates

Spheroids • Set of parameters that represent a model of the earth’s size and shape • Based on an ellipse with 2 radii – Semimajor axis (longer) and the semiminor (shorter)

Spheroids • The Earth is not a perfect spheroid. Different spheroids are used in different parts of the world to create the best possible model of the Earth’s curvature in each location.

Spheroids

Datums • A Datum is a spheroid, plus the definition of the relationship between the Earth and the coordinates on the spheroid.

Datums • There are four datums commonly used in Montana: NAD 27, WGS 84, NAD 83, and NAD 83 HARN. The latitude and longitude of a point on the ground is different in each datum.

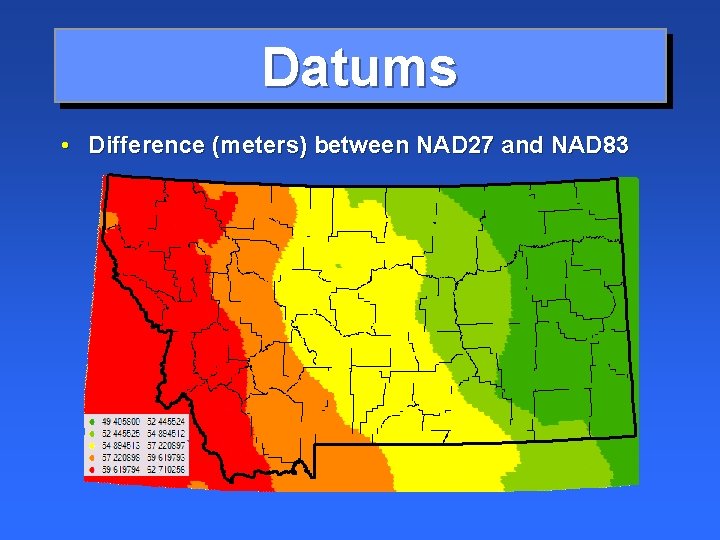
Datums • Difference (meters) between NAD 27 and NAD 83

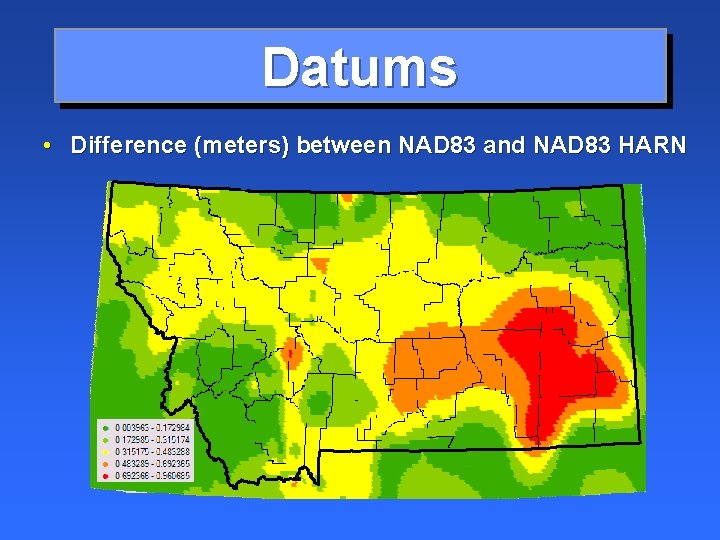
Datums • Difference (meters) between NAD 83 and NAD 83 HARN

Projected Coordinate Systems • Define locations on a 2 -D surface • Traditional planar coordinates • Can allow easy measurement, calculation, and/or visual interpretation of distances and areas

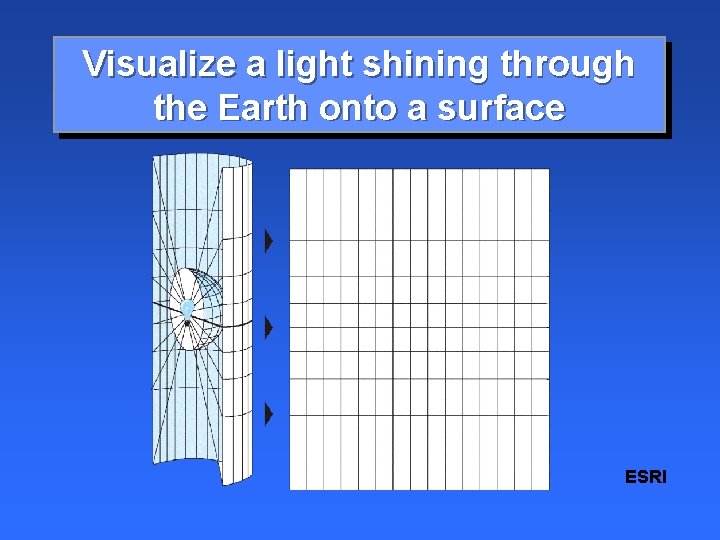
Visualize a light shining through the Earth onto a surface ESRI

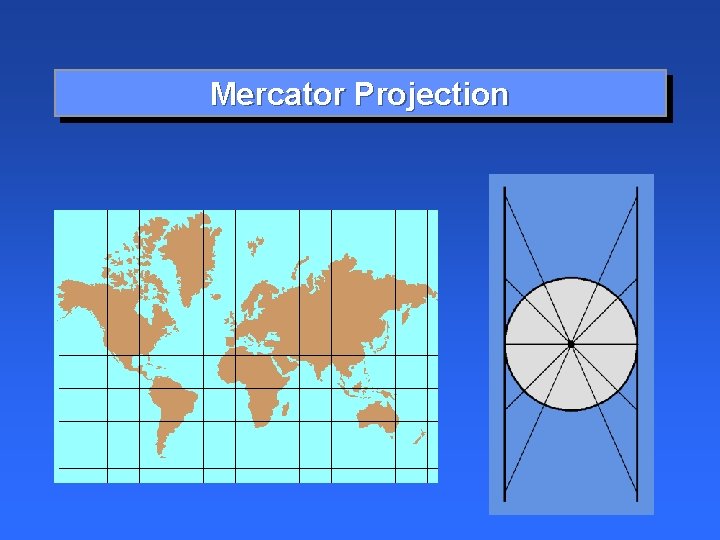
Mercator Projection

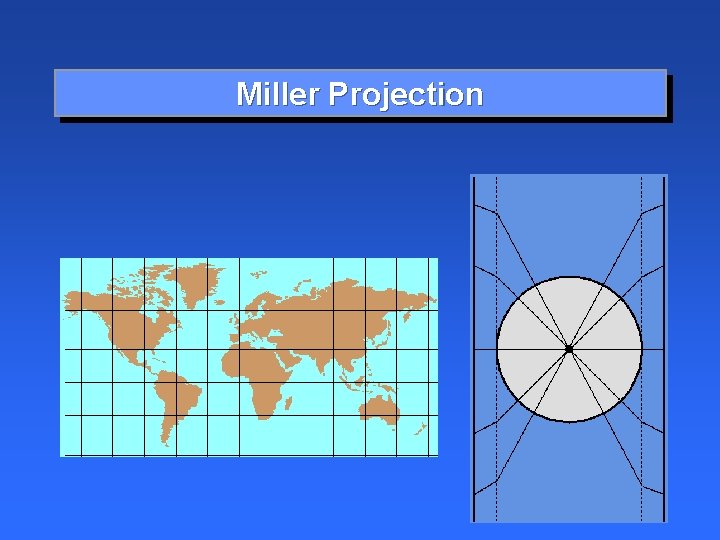
Miller Projection

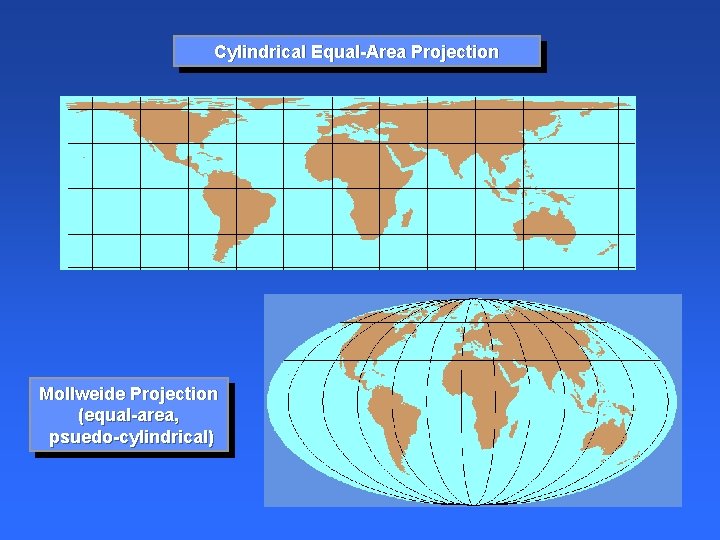
Cylindrical Equal-Area Projection Mollweide Projection (equal-area, psuedo-cylindrical)

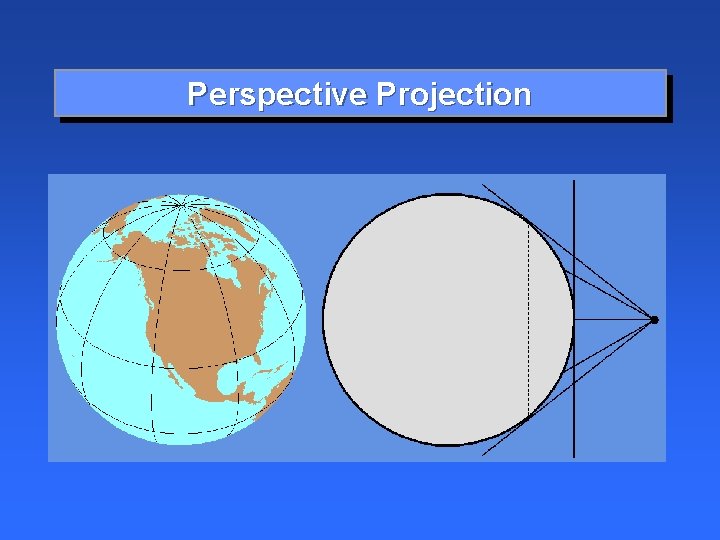
Perspective Projection

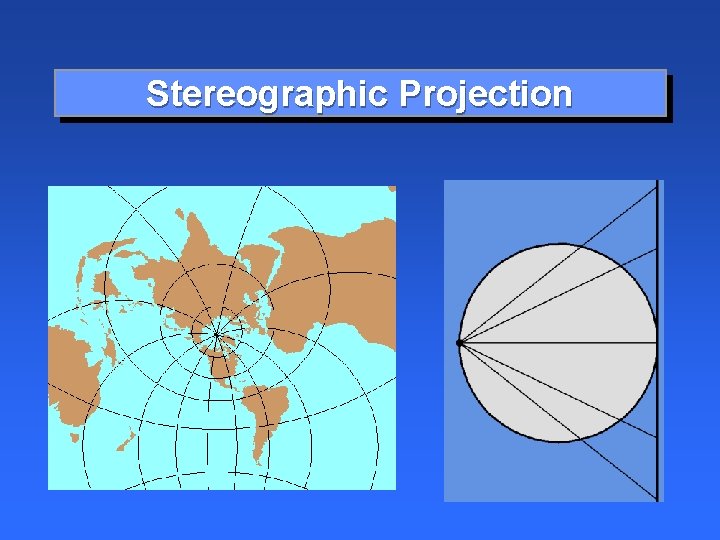
Stereographic Projection

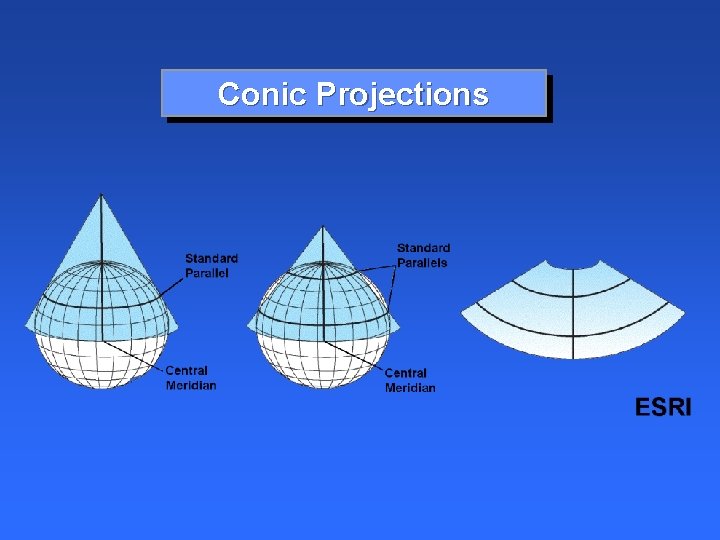
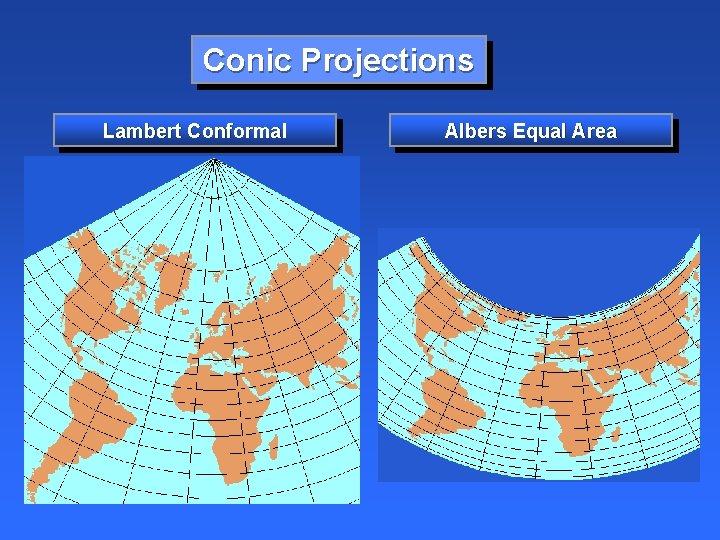
Conic Projections

Conic Projections Lambert Conformal Albers Equal Area

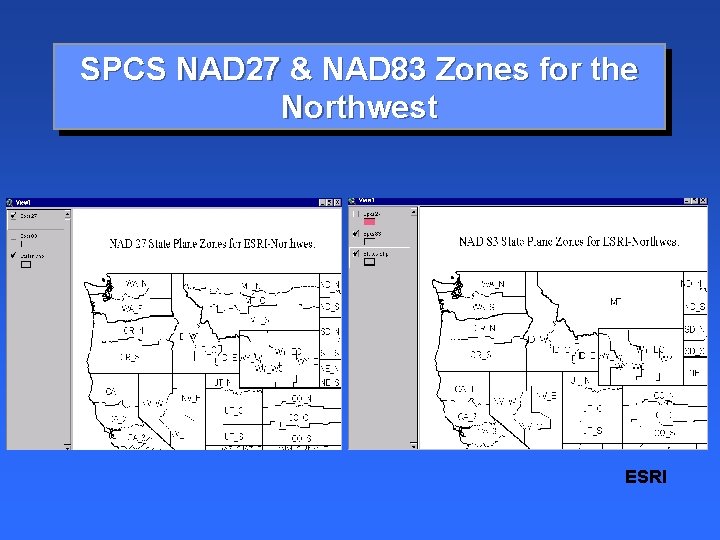
Standardized Coordinate Systems There an infinite number of coordinate systems possible, which can be created by choosing a projection and then tailoring its parameters to fit any region on the globe. Standardized coordinate systems have been developed to simplify the process of choosing a system. The two most common standard systems used in the United States are the State Plane Coordinate system and the Universal Transverse Mercator system.

SPCS NAD 27 & NAD 83 Zones for the Northwest ESRI

UTM

Choosing a Projection: Checking Accuracy To find the true area of polygons, project them to an equal-area projection and recalculate their areas. To find the true distance between two points: http: //www. ngs. noaa. gov/cgi-bin/Inv_Fwd/inverse. prl

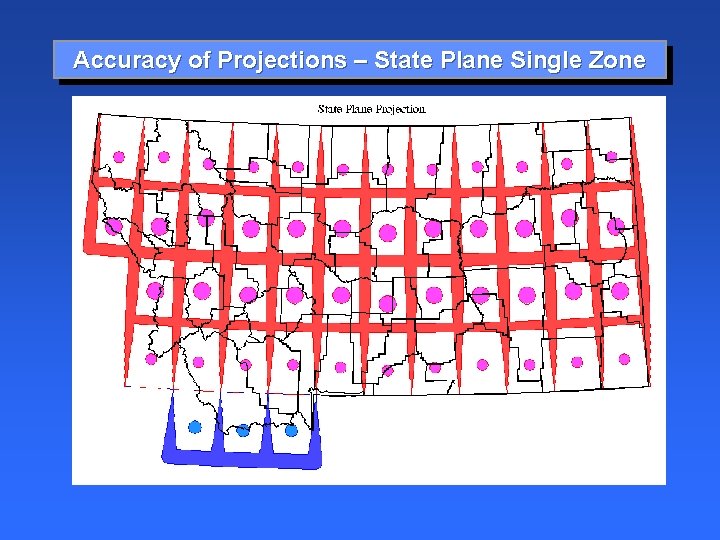
Accuracy of Projections – State Plane Single Zone

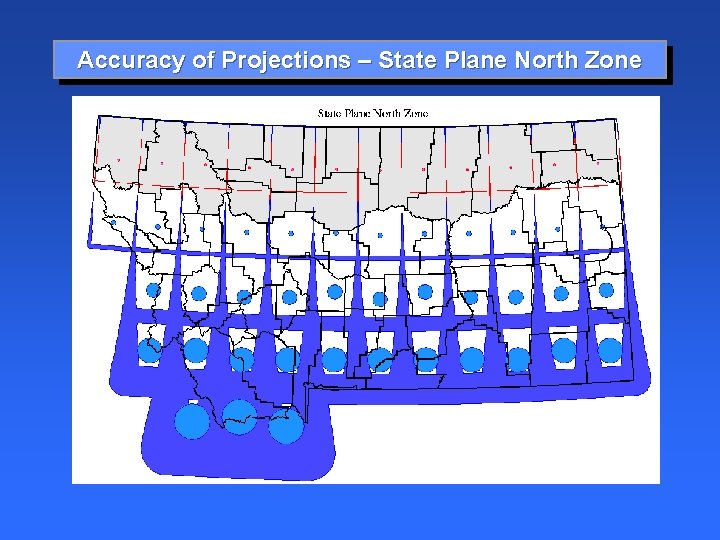
Accuracy of Projections – State Plane North Zone

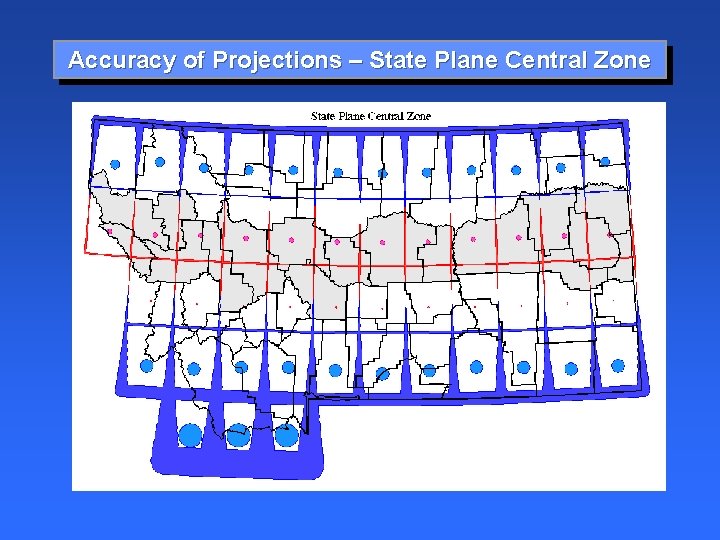
Accuracy of Projections – State Plane Central Zone

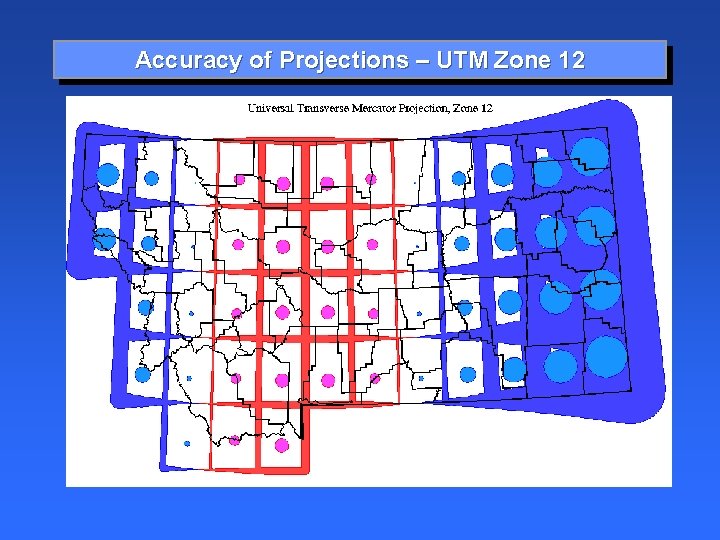
Accuracy of Projections – UTM Zone 12

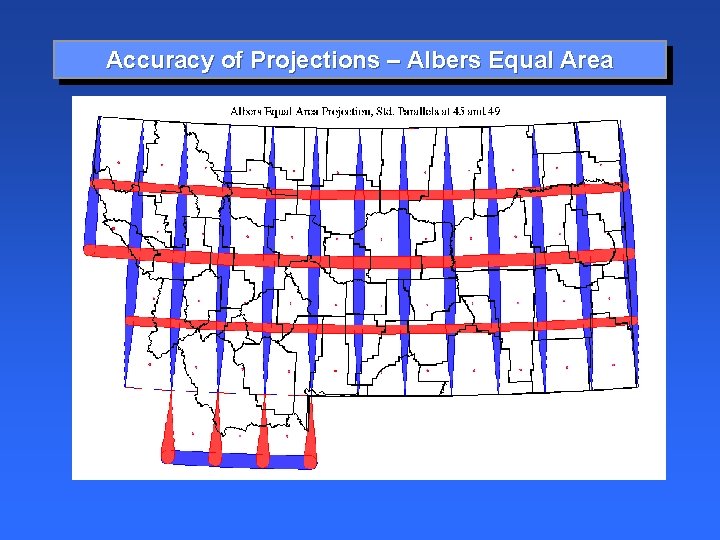
Accuracy of Projections – Albers Equal Area

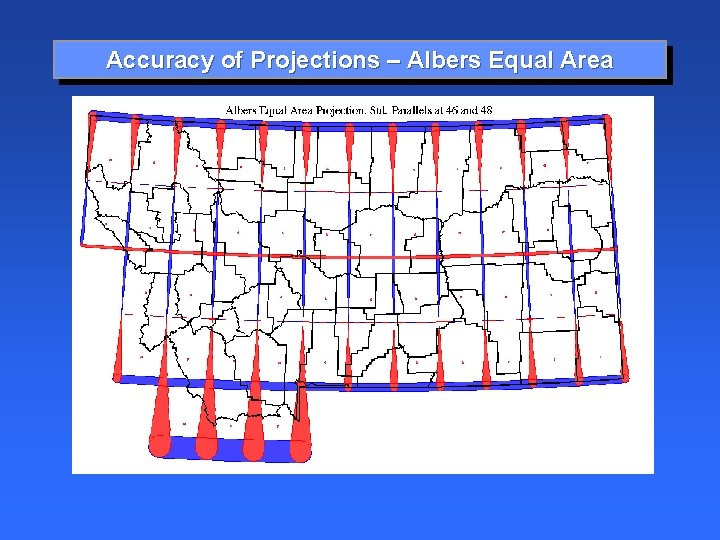
Accuracy of Projections – Albers Equal Area

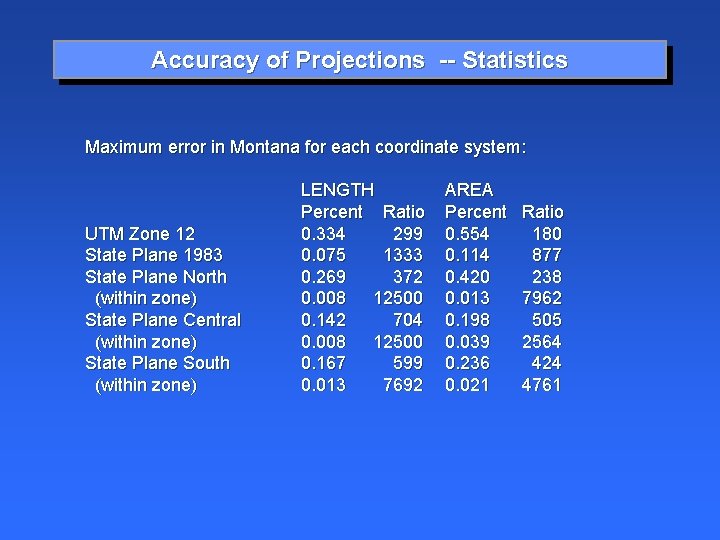
Accuracy of Projections -- Statistics Maximum error in Montana for each coordinate system: UTM Zone 12 State Plane 1983 State Plane North (within zone) State Plane Central (within zone) State Plane South (within zone) LENGTH Percent Ratio 0. 334 299 0. 075 1333 0. 269 372 0. 008 12500 0. 142 704 0. 008 12500 0. 167 599 0. 013 7692 AREA Percent 0. 554 0. 114 0. 420 0. 013 0. 198 0. 039 0. 236 0. 021 Ratio 180 877 238 7962 505 2564 424 4761

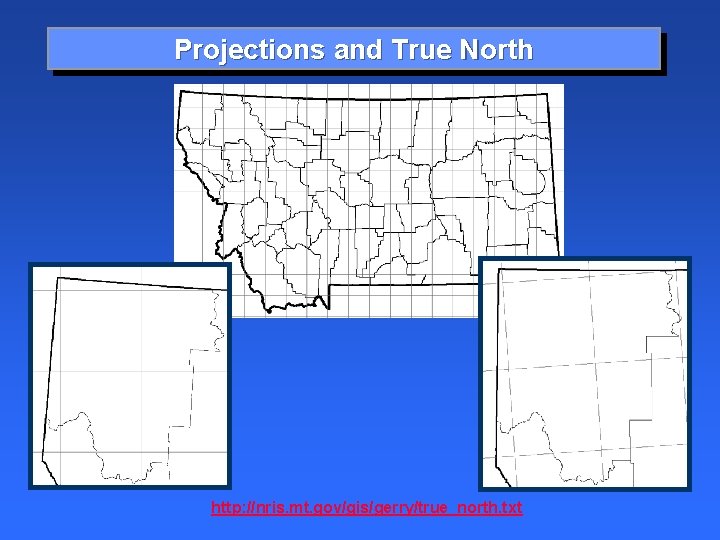
Projections and True North http: //nris. mt. gov/gis/gerry/true_north. txt