Map Projection Theory and Usage What is a

Map Projection Theory and Usage

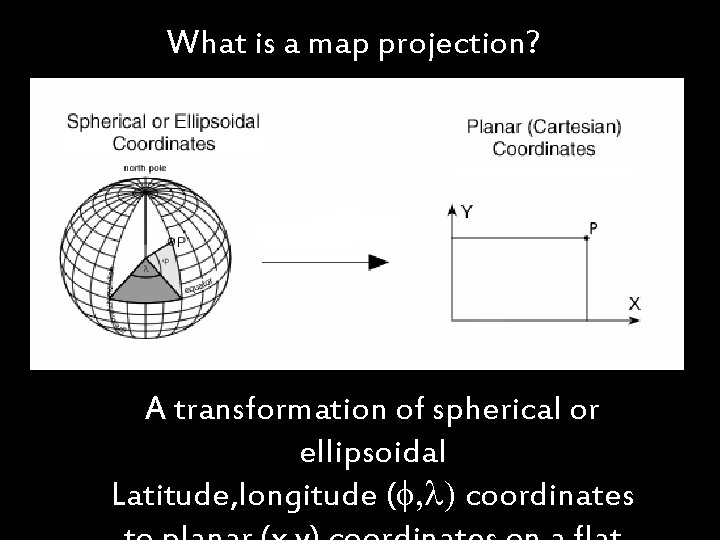
What is a map projection? A transformation of spherical or ellipsoidal Latitude, longitude (f, l) coordinates

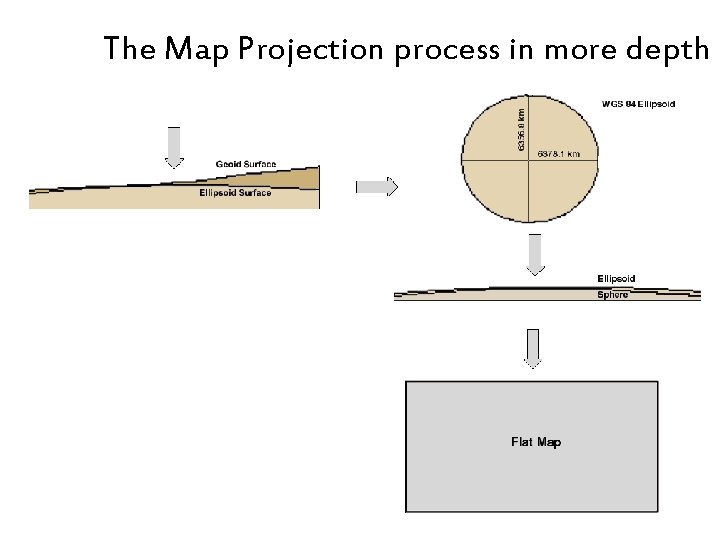
The Map Projection process in more depth

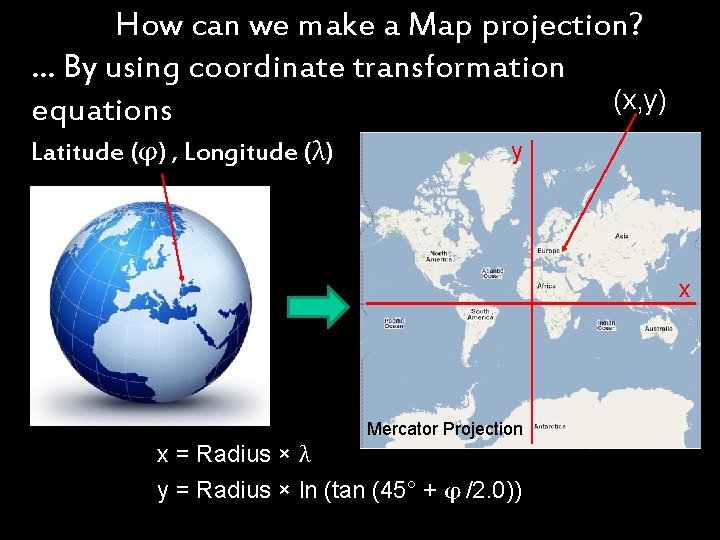
How can we make a Map projection? … By using coordinate transformation (x, y) equations Latitude (φ) , Longitude (λ) y x Mercator Projection x = Radius × λ y = Radius × ln (tan (45° + φ /2. 0))

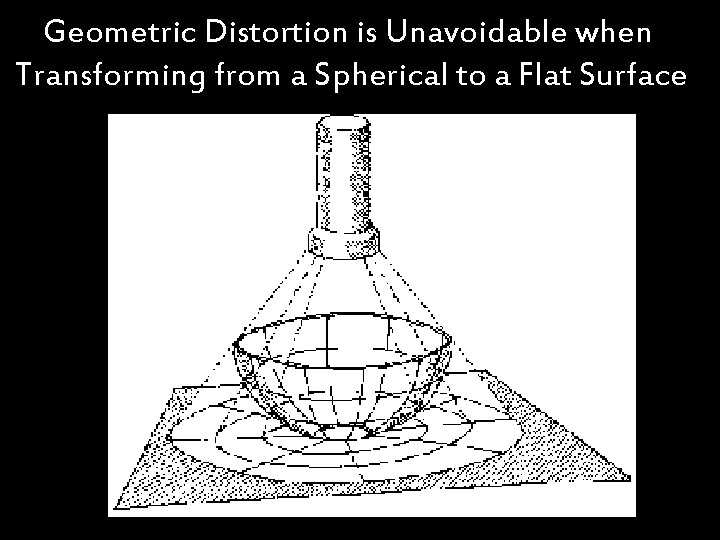
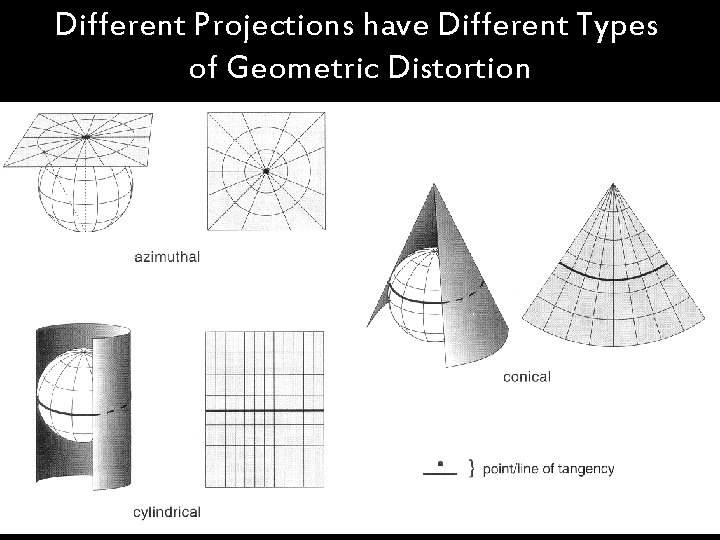
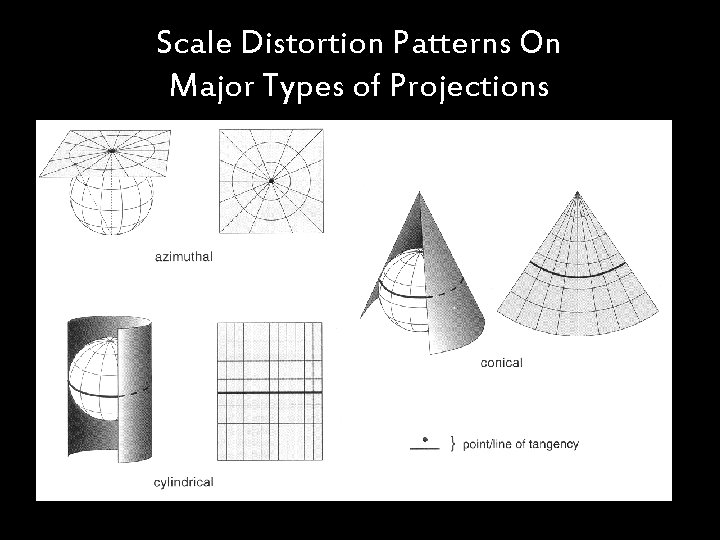
Geometric Distortion is Unavoidable when Transforming from a Spherical to a Flat Surface

Different Projections have Different Types of Geometric Distortion

Understanding Scale Distortion by Studying Scale Factors across the Projection Scale Factor = Denominator of Principal Scale RF _____________ Denominator of Actual Scale RF RF stands for Representative Fraction

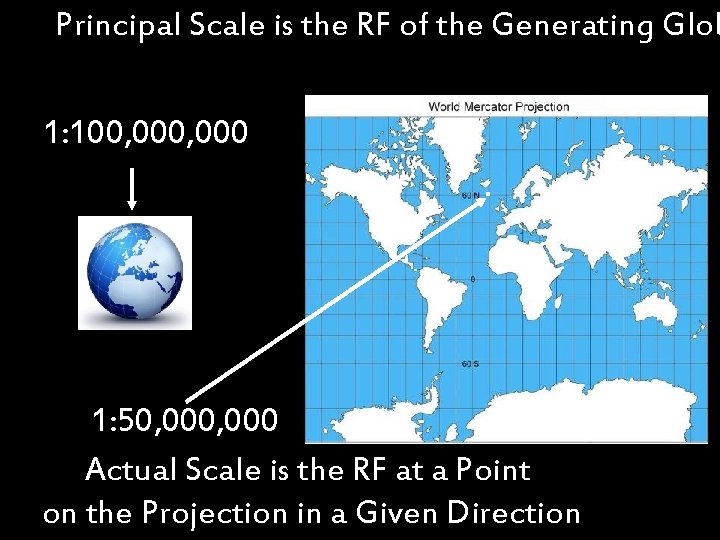
Principal Scale is the RF of the Generating Glob 1: 100, 000 1: 50, 000 Actual Scale is the RF at a Point on the Projection in a Given Direction

Scale Factor 2. 00 times as 100, 000 ______ = large 50, 00 at the point 0

Scale Distortion Patterns On Major Types of Projections

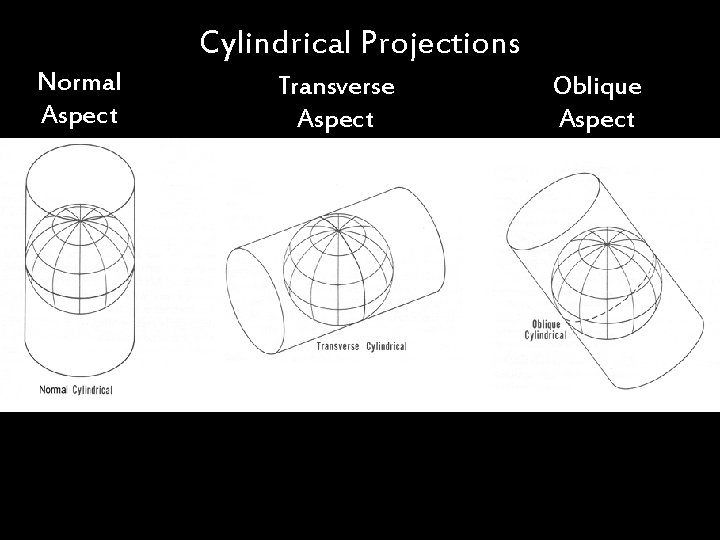
Cylindrical Projections Normal Aspect Transverse Aspect >1 . S. F. =1 S. F. >1 . =1 S. F . >1 S. F. >1 1 S. F. > S. F 1 S. F. = 1 S. F. > Oblique Aspect

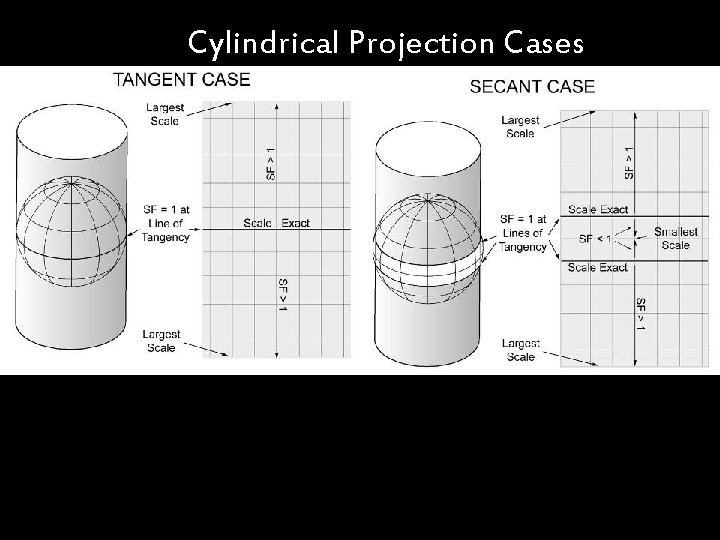
Cylindrical Projection Cases

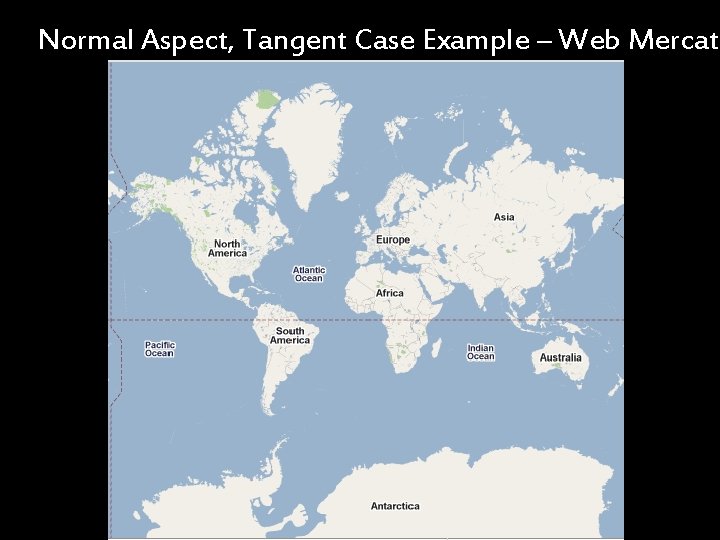
Normal Aspect, Tangent Case Example – Web Mercato

Transverse Aspect, Secant Case Example – UTM Zones

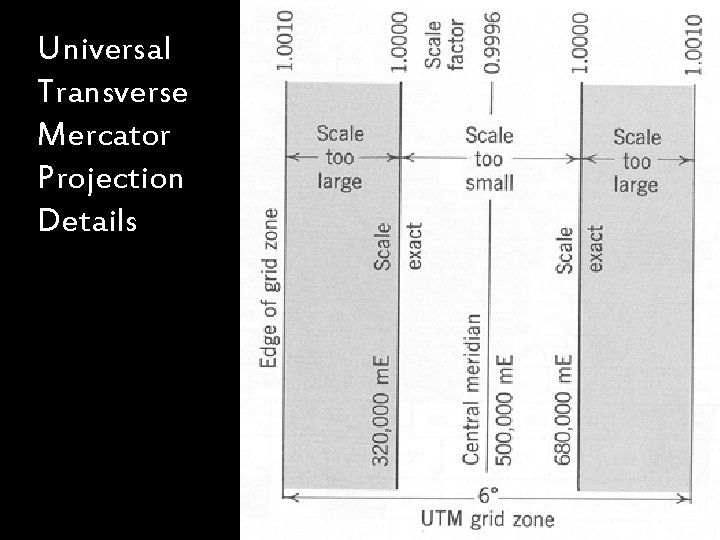
Universal Transverse Mercator Projection Details

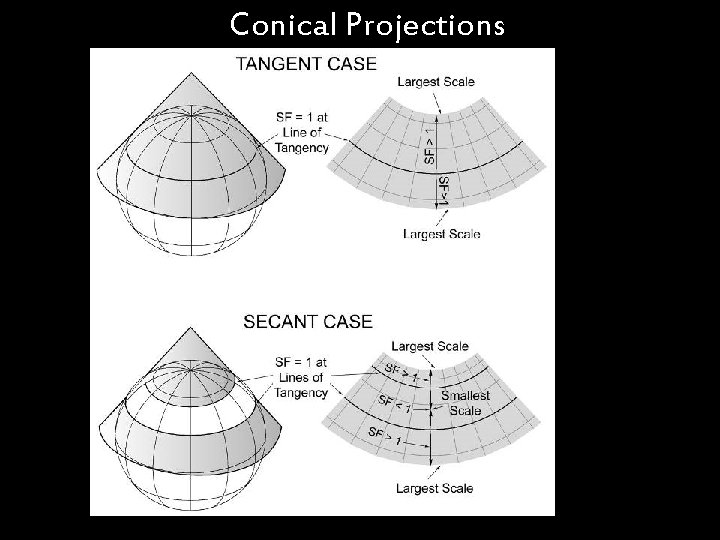
Conical Projections

Normal Aspect, Secant Case Example --Sectional Aeronautical Charts --

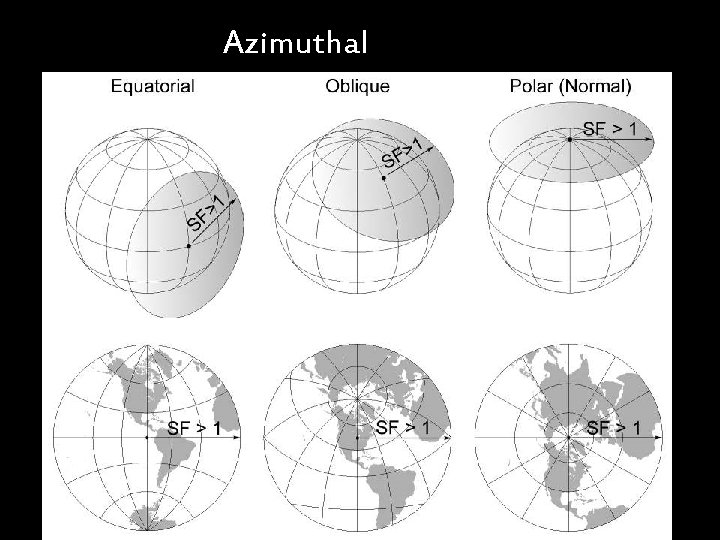
Azimuthal Projections

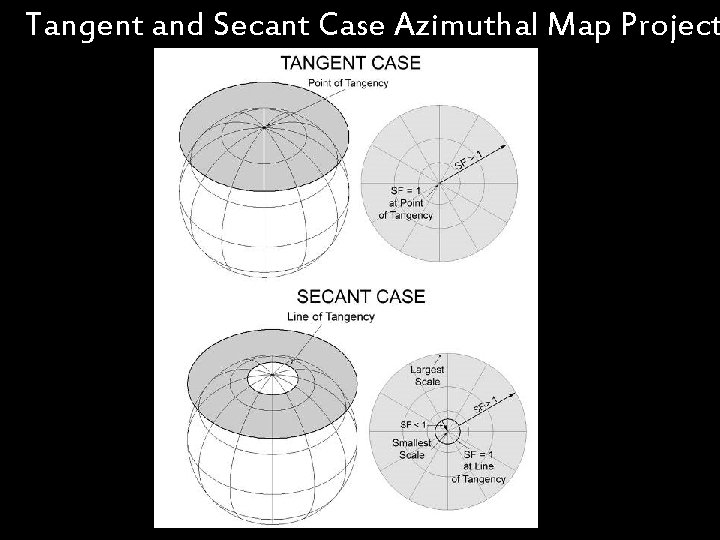
Tangent and Secant Case Azimuthal Map Project

Polar Aspect, Secant Case Example --Universal Polar Stereographic Grid Zones --

Oblique Aspect, Tangent Case Example --Great Circle Sailing Chart on Gnomonic Projection--

Oblique Aspect, Tangent Case Example -- Earth Day and Night on Orthographic Projection--

Oblique and Equatorial Aspect, Tangent Case Examples -- Rotating Globes on Orthographic Projection-- Which one is spinning correctly?

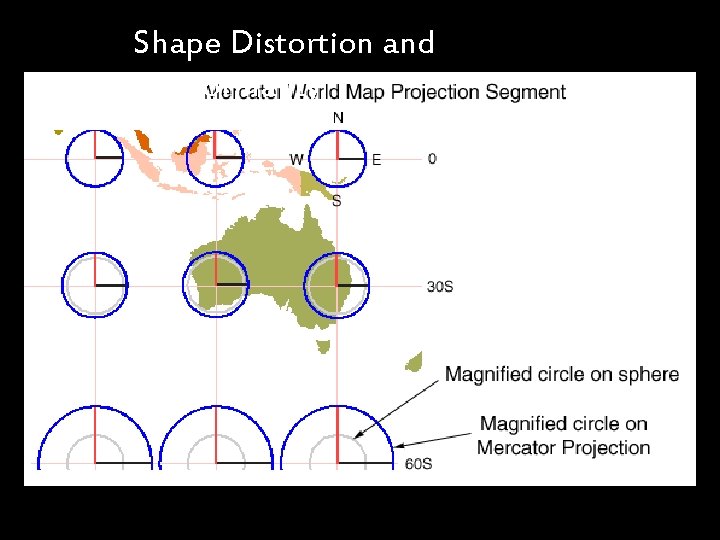
Shape Distortion and Conformality

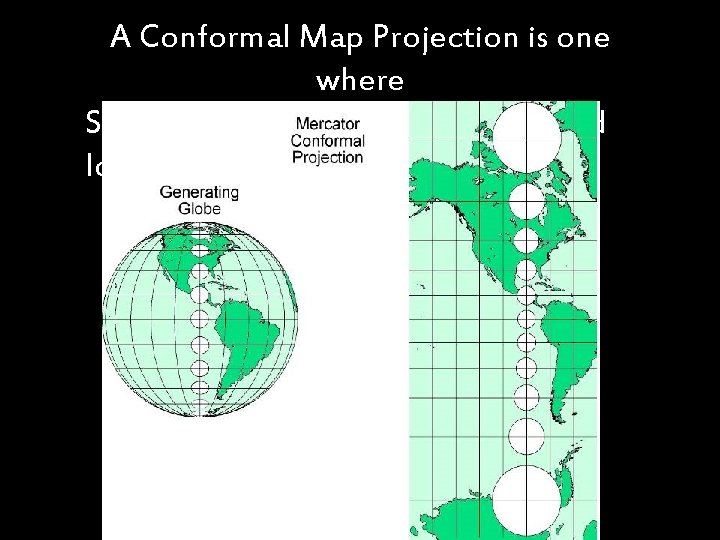
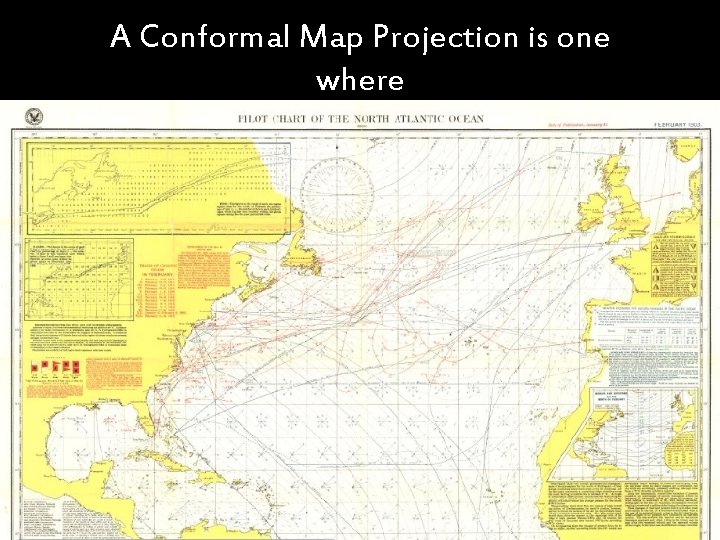
A Conformal Map Projection is one where Shapes and Directions are preserved locally

A Conformal Map Projection is one where Shapes and Directions are preserved locally

A Conformal Map Projection is one where Shapes and Directions are preserved locally

Normal Aspect, Secant Case Conformal Projection --Sectional Aeronautical Charts --

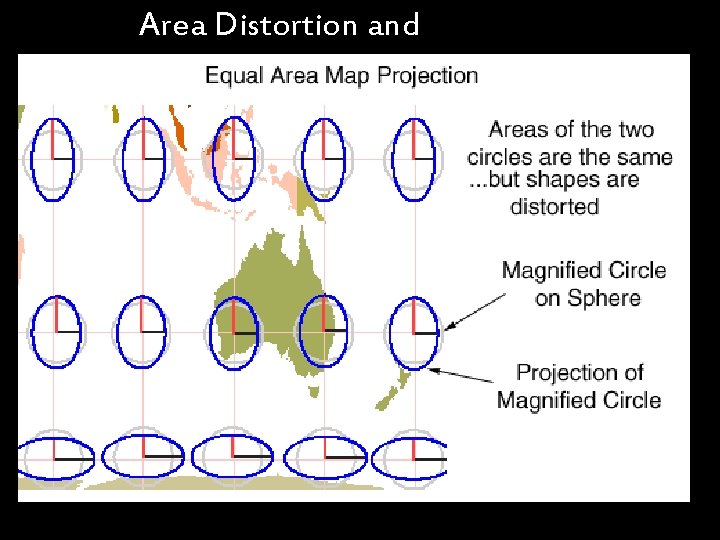
Area Distortion and Equivalency

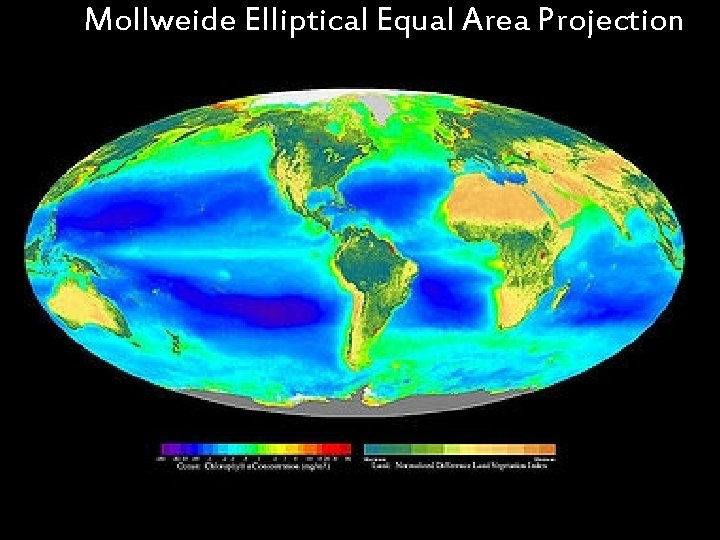
Mollweide Elliptical Equal Area Projection

Mollweide Elliptical Equal Area Projection

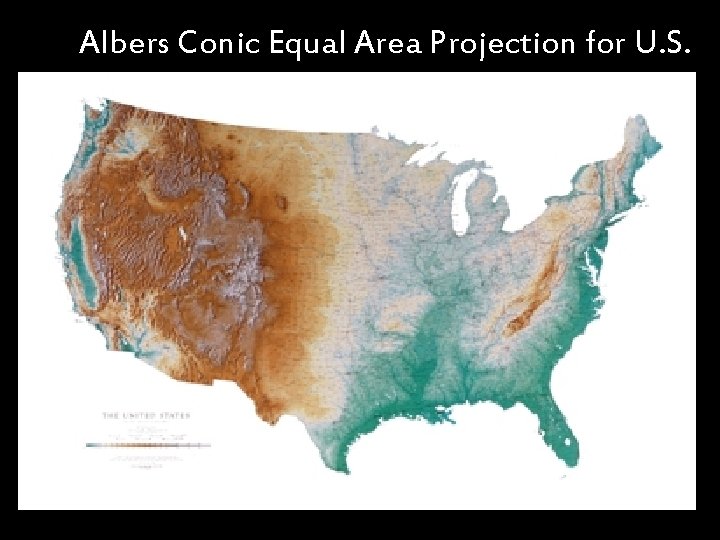
Albers Conic Equal Area Projection for U. S.

No Flat Map can be Conformal and Equal Area at the same time …Only a Globe can be!