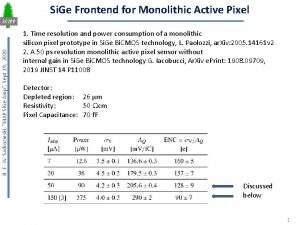
Map Overlay Algorithm Map 1 Vegetation Map 2

Map Overlay Algorithm

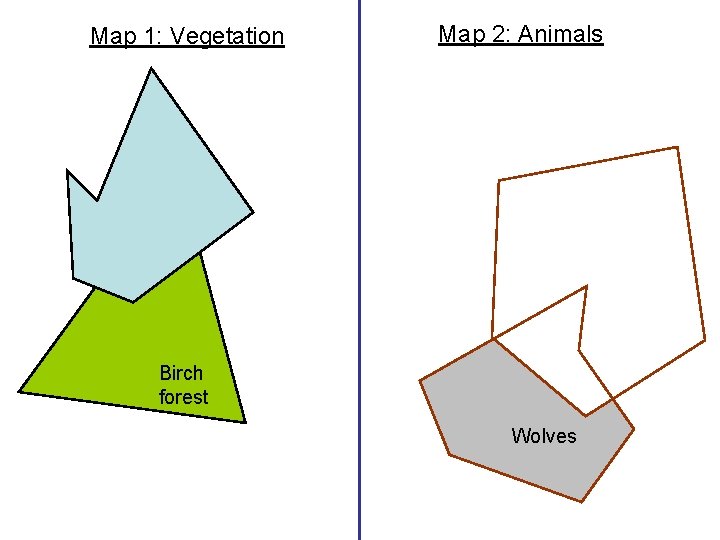
Map 1: Vegetation Map 2: Animals Birch forest Wolves

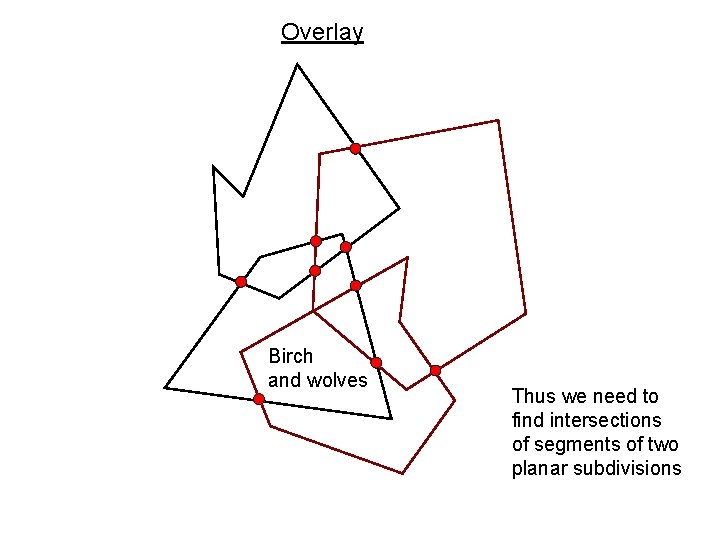
Overlay Birch and wolves Thus we need to find intersections of segments of two planar subdivisions

Overlay of two subdivisions • S 1 and S 2 are two subdivisions (planar graphs), given in the form of DCEL’s • Our goal is to compute the DCEL for the overlay O(S 1, S 2) • Note: f is a face of O (S 1, S 2) if and only if there are two faces f 1 from S 1 and f 2 from S 2 such that f is the maximal connected component of the intersection f 1 and f 2

Strategy • Take the union of DCEL’s of S 1 and S 2 • This union is NOT a valid DCEL (does not represent planar subdivision) • We need to transform this union into a valid DCEL, i. e. to compute new half-edge records, face records, and vertex records • For each face record f in O (S 1, S 2) we also need to report information about faces f 1 from S 1 and f 2 from S 2 such that f is the maximal connected component of the intersection f 1 and f 2 • Recall: any half-edge in DCEL is oriented so that the face it bounds lies to the left. Therefore we can use an unchanged half-edge record from S 1 in O(S 1, S 2) if and only if it is not intersected by any edge from S 2, and vice versa

Algorithm - preparation • By complexity of a subdivision we mean the num. of vertices + the num. of edges + the num. of faces • In what follows, k will denote the complexity of D (the resulting subdivision), and n will denote the sum of complexities of S 1 and S 2 • Note: due to the Euler's formula, the complexity of a connected planar subdivision is O (number of edges)

Algorithm - preparation • Based on the plane sweep algorithm for segment intersections • We use it to find intersections of edges from S 1 and S 2 • Data structures to be used: Q (event queue) and T (status structure) as before • Additionally, D will be new DCEL • Together with edges in T, we store pointers to the corresponding half-edges in D • Initially, D contains the union of DCEL’s of S 1 and S 2 • During the algorithm, D will be transformed into the correct DCEL for the overlay O (S 1, S 2)

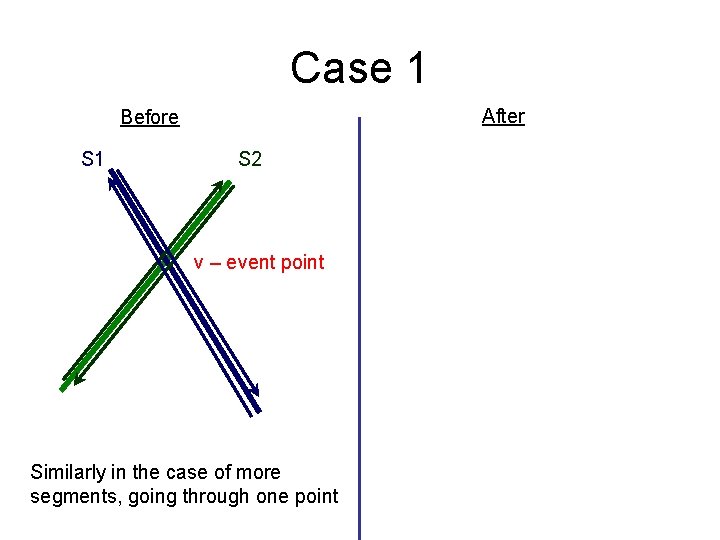
Algorithm – handling an event point • We update T and Q as in the case of segment intersection algorithm • If event point involves segments from only one of S 1 or S 2, nothing else happens • If not, we must create new half-edges in D • This involves several possible case: § an edge of S 1 crosses and edge of S 2 § an edge from S 1 passes through a vertex of S 2 (or vice versa) § a common vertex

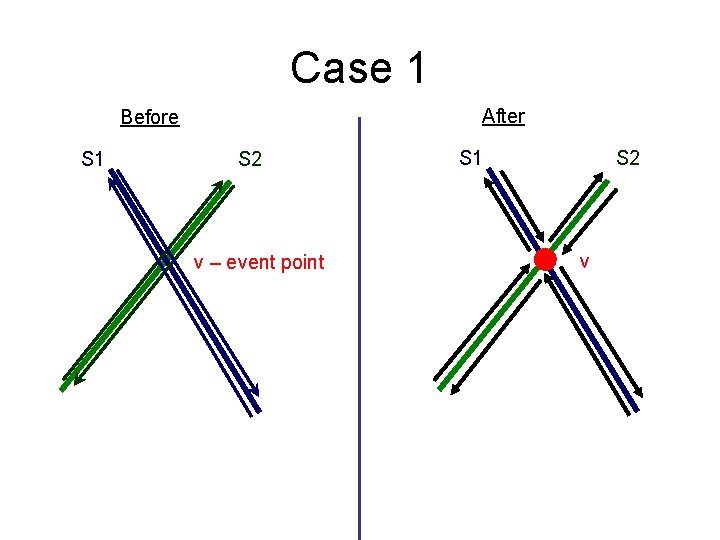
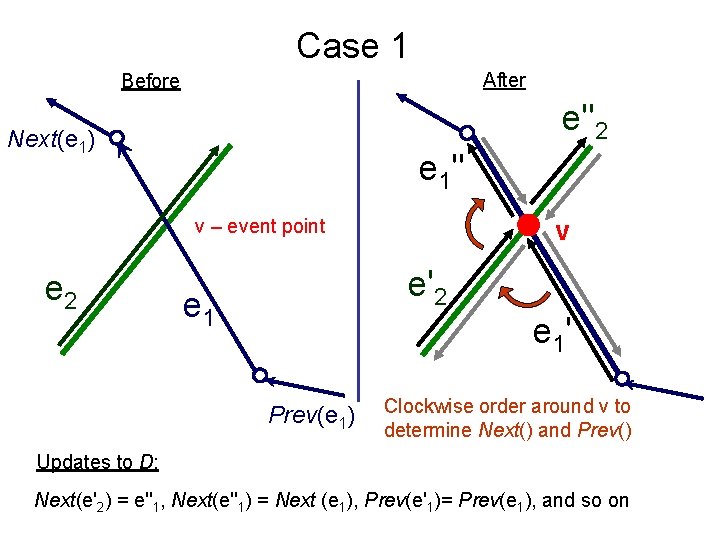
Case 1 After Before S 1 S 2 v – event point Similarly in the case of more segments, going through one point

Case 1 After Before S 1 S 2 v – event point S 1 S 2 v

Case 1 After Before e''2 Next(e 1) e 1'' v – event point e 2 v e'2 e 1' Prev(e 1) Clockwise order around v to determine Next() and Prev() Updates to D: Next(e'2) = e''1, Next(e''1) = Next (e 1), Prev(e'1)= Prev(e 1), and so on

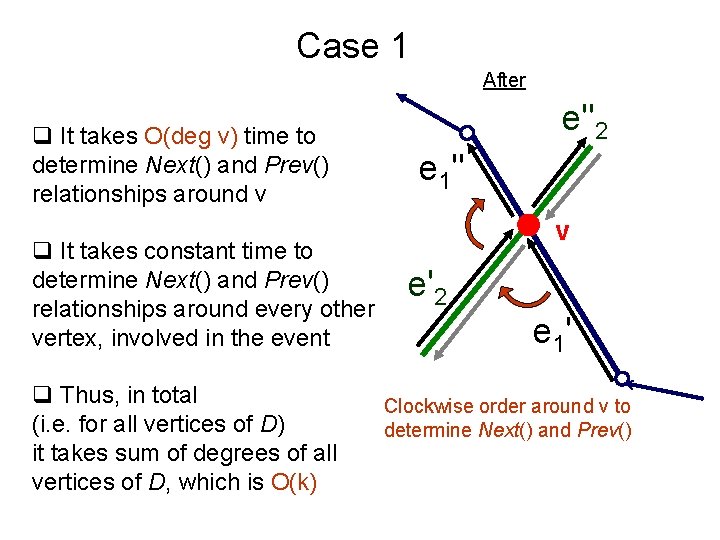
Case 1 After q It takes O(deg v) time to determine Next() and Prev() relationships around v q It takes constant time to determine Next() and Prev() relationships around every other vertex, involved in the event q Thus, in total (i. e. for all vertices of D) it takes sum of degrees of all vertices of D, which is O(k) e''2 e 1'' v e'2 e 1' Clockwise order around v to determine Next() and Prev()

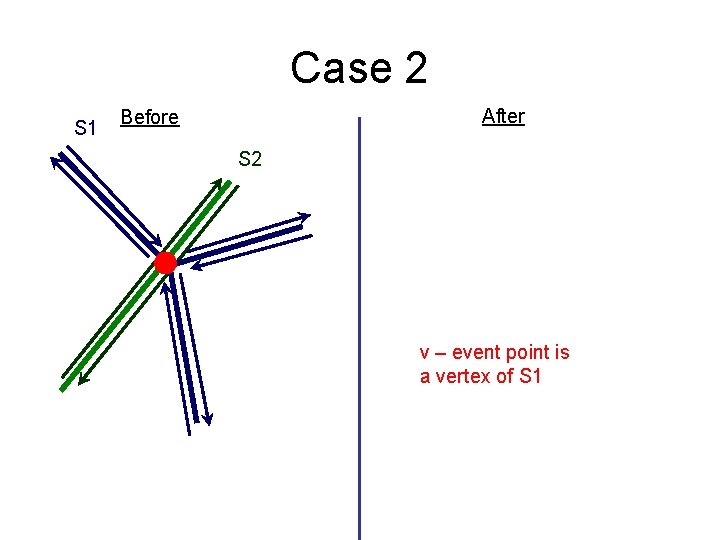
Case 2 S 1 After Before S 2 v – event point is a vertex of S 1

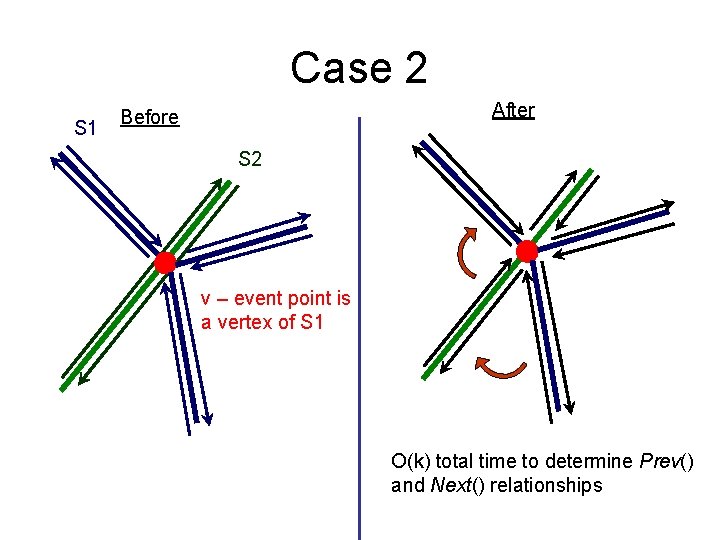
Case 2 S 1 After Before S 2 v – event point is a vertex of S 1 O(k) total time to determine Prev() and Next() relationships

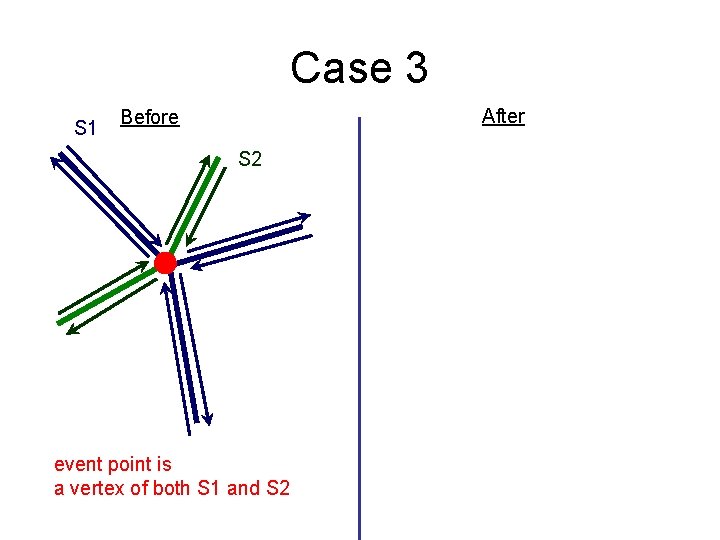
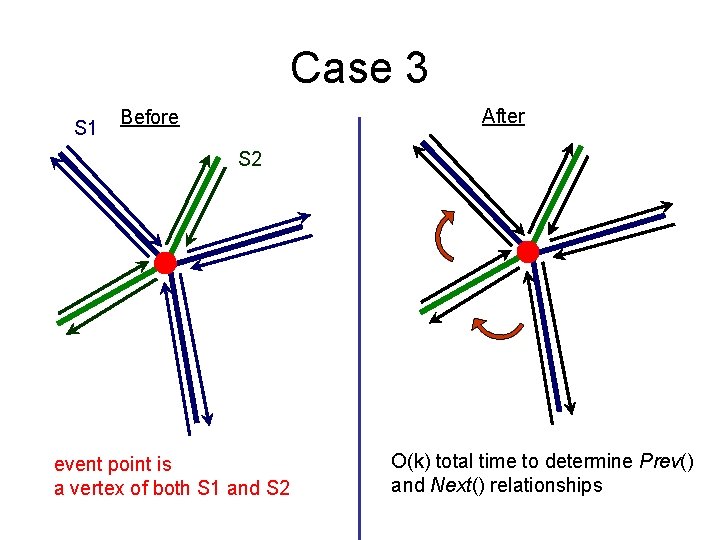
Case 3 S 1 After Before S 2 event point is a vertex of both S 1 and S 2

Case 3 S 1 After Before S 2 event point is a vertex of both S 1 and S 2 O(k) total time to determine Prev() and Next() relationships

Total Time • Let k be the complexity of D and n be the sum of complexities of S 1 and S 2 • Then, according to the time required for the segment intersection algorithm, the previous part of the map overlay algorithm takes O(n log n + k log n) time

• During the plane sweep: Some remarks 1. for each half-edge in D, we can record the corresponding halfedge from S 1 or S 2 - this will allow us to find the corresponding face record from S 1 or S 2 by looking at Incident. Face () 2. for each vertex v of S 1 which does not belong to any edge of S 2, we can determine a face of S 2 that contains it by looking and the edges of S 2 in the status T, immediately to the left and to the right of v (and vice versa, for each v of S 2) 3. for each vertex we will record the half-edge of D that lies immediately to the left of the vertex with respect to the current position of the sweep line • By traversing the edges of D, we can find all boundary cycles in O(k) time, where k is the complexity of D • This will help us to create face records in D • Moreover, using 1. and 2. from the above, for each new face record we will be able to find faces f 1 and f 2 of S 1 and S 2, respectively, such that f is the intersection of f 1 and f 2

Face records in D • We know all boundary cycles of D • Problem: which of them are outer boundaries of faces and which are inner cycles, i. e. boundaries of holes inside faces? • It can be solved as follows § Look at the leftmost vertex of the cycle § If half-edges from the boundary of the cycle, that are incident to this vertex, form an angle < 180 o, it is outer cycle, otherwise it is an inner cycle

Face records in D • Another Problem: which of outer cycles lie in a given inner cycle? • To decide, we will construct a special graph G as follows: § vertices of G are boundary cycles § additional vertex corresponds to the imaginary outer boundary of the unbounded face § two vertices are joined by an edge if and only if one of the corresponding cycles is the boundary of a hole and the other cycle has a half-edge immediately to the left of the leftmost vertex of that hole cycle § if there is no such half-edge, then the vertex is linked to the vertex, corresponding to the unbounded face • It takes O(k) time to construct G

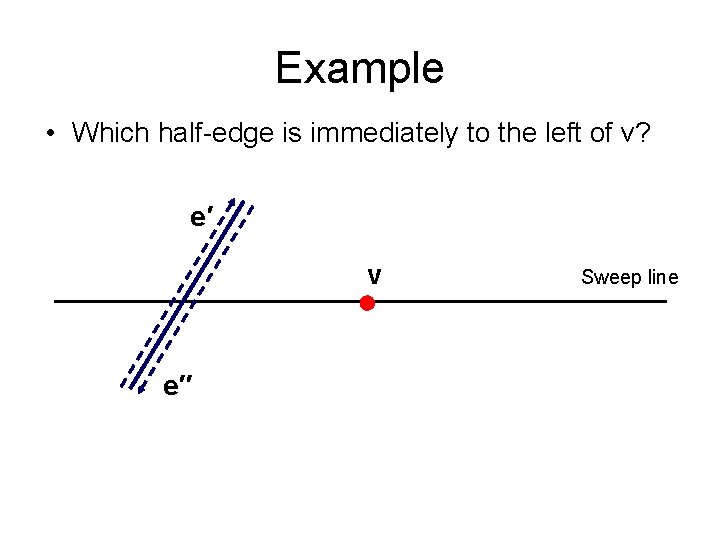
Example • Which half-edge is immediately to the left of v? e′ v e′′ Sweep line

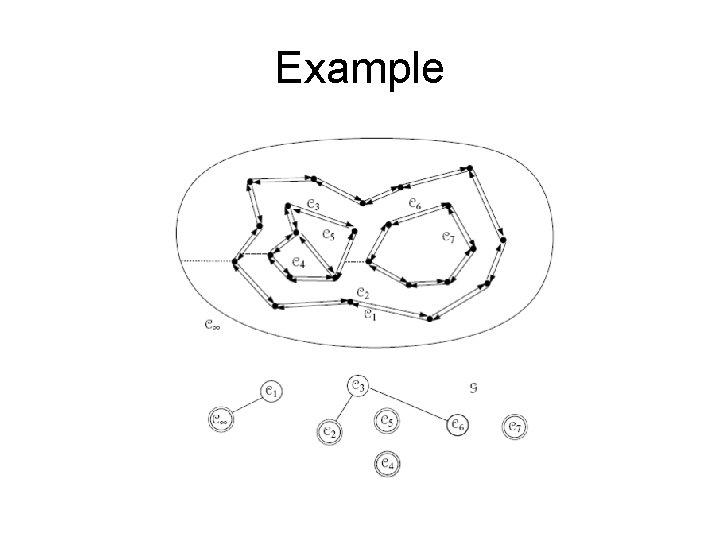
Example

Lemma 2. 5 • Each connected component of the graph G corresponds exactly to the set of cycles incident to one face • Thus, we need to determine connected components of G • It takes O(k) time to do it (using e. g. a depth-first search)

Total time required for map overlay • Let n be the sum of complexities of S 1 and S 2 and k be the complexity of D • Plan sweep: O (n log n + k log n) • After the plane sweep: § Finding boundary cycles: O(k) § Constructing the graph: O(k) § Finding connected components of G: O(k) § Thus the total time is still O (n log n + k log n)

Algorithm MAPOVERLAY(S 1, S 2) Input. S 1 and S 2 stored as DCEL’s Output. The overlay of S 1 and S 2 stored in DCEL D q Copy DCEL’s for S 1 and S 2 to D q Plane sweep: compute all intersections between edges from S 1 and S 2 q In addition, do the following during the plane sweep: q Update D if the event involves edges of both S 1 and S 2 (create new half-edges and update Next() and Prev() info) q Store the half-edge immediately to the left of the event point at the vertex in D representing it (will be required later to create G) q For each v from S 1 which does not belong to any edge of S 2, record the face of S 2 in which it is contained (and similarly for vertices of S 2) Now D is the DCEL for O(S 1, S 2), except that the information about the faces has not been computed yet

q Determine the boundary cycles in O(S 1, S 2) by traversing D. q Construct the graph G whose vertices correspond to boundary cycles and whose edges connect each hole cycle to the left of its leftmost vertex q Compute connected components of G q For each connected component in G Do q Let C be the unique outer boundary cycle in the component and let f denote the face bounded by this cycle q create a face record for f q set Outer. Component (f) to some half-edge of C q construct the list Inner. Components (f) consisting of pointers to one half-edge in each hole cycle in the component q let the Incident. Face() pointers of all half-edges in the cycles point to the face record of f q End Do q Label each face of O(S 1, S 2) with the names of the faces of S 1 and S 2 containing it