Manufacturing Cell Design Problem Formulation Team 2 Mingang

Manufacturing Cell Design - Problem Formulation Team #2 Mingang Fu Lin Ben Kuowei Chen

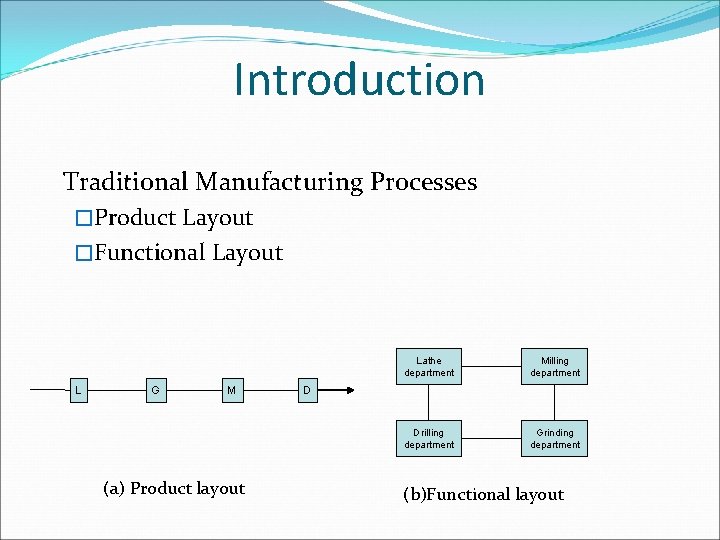
Introduction Traditional Manufacturing Processes �Product Layout �Functional Layout L G M (a) Product layout Lathe department Milling department Drilling department Grinding department D (b)Functional layout

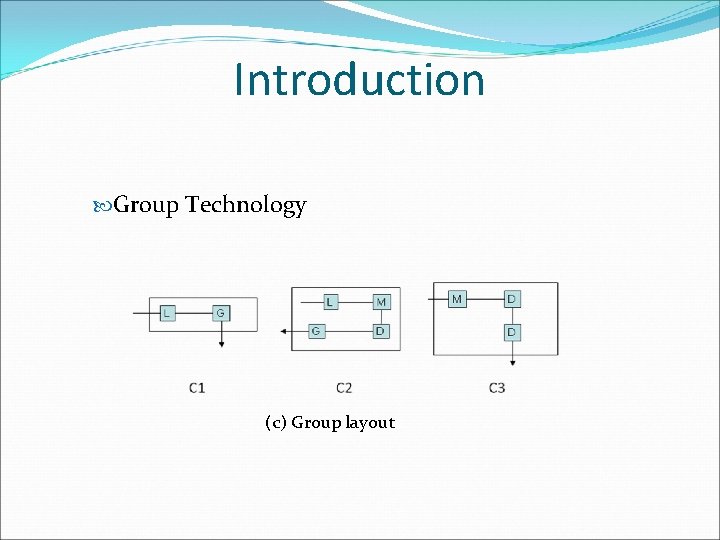
Introduction Group Technology (c) Group layout

Problem Description �A part family may consist of groups of parts requiring similar and sometimes identical operation processes, materials, and tools. �A manufacturing cell is formed by the machines which are required to produce a part family. �Goal: form a manufacturing system that consists of cells �to maximize the moves of parts processed within the cells, at the same time, to minimize the parts flow between cells

Problem Description �Example:

• Notations: Formulation 1 i and j are machine indexes (i, j = 1, 2, …, Nm). k is a part index (k = 1, 2, 3, …, Np) c is a cell index (c = 1, 2, 3, …, Nc) is the production volume of part k is available transfer units per trip for part k using a transfer device is the upper limit of cell size is the number of trips made by part k between machines i and j: Where indicates the smallest integer value greater than or equal to w. • Variables:

Formulation 1 �Objective function: �Constraints:

Formulation 1 - Example Nm = 7, Np = 7, Nc = 3 Objective X function value = 2 11=1, X 21=1 X 32=1, X 42=1, X 52=1 X 63=1, X 73=1

Formulation 1 - Example X 21=1, X 51=1 X 32=1, X 42=1, X 62=1 X 13 Objective =1, X 73=1 function value = 10

Formulation 2 � m machines and n parts with k cells and there a total of k(m+n) variables and (m+n) constrains.

� With the size of problem increases, the model becomes too large to handle. To overcome this problem, we can change the integer programming model with following declaration: � Then we define “group efficiency” as following and maximize it.

Formulation 2 - Example Cell 1, Family 1 Cell 2, Family 2 Cell 3, Family 3 X 1=1, X 2=1, X 3=2, X 4=2, X 5=2, X 6=3, X 7=3; Y 1=1, Y 2=1, Y 3=2, Y 4=2, Y 5=2, Y 6=3, Y 7=3 X 11=1, X 21=1, X 31=0, …X 71=0 X 12=0, X 22=0, X 32=1, X 42=1, X 52=1, X 62=0, X 72=0 X 13=0, …X 53=0, X 63=1, X 73=1 Y 11=1, Y 21=1, Y 31=0, …Y 71=0 Y 12=0, Y 22=0, Y 32=1, Y 42=1, Y 52=1, Y 62=0, Y 72=0 Y 13=0, …Y 53=0, Y 63=1, Y 73=1 e=17, ev=10, eo=10, Gamma=7/27

Formulation 2 - Example X 1=3, X 2=1, X 3=2, X 4=2, X 5=1, X 6=2, X 7=3; Y 1=1, Y 2=3, Y 3=2, Y 4=2, Y 5=3, Y 6=2, Y 7=1 e=17, ev=0, eo=0, Gamma=17/17=1, best

Thank you !