Mantle convective heat flux into continental lithosphere Shijie

Mantle convective heat flux into continental lithosphere Shijie Zhong Department of Physics, University of Colorado at Boulder, USA For Geo-neutrino Meeting at IHEP Beijing, China July 22, 2017

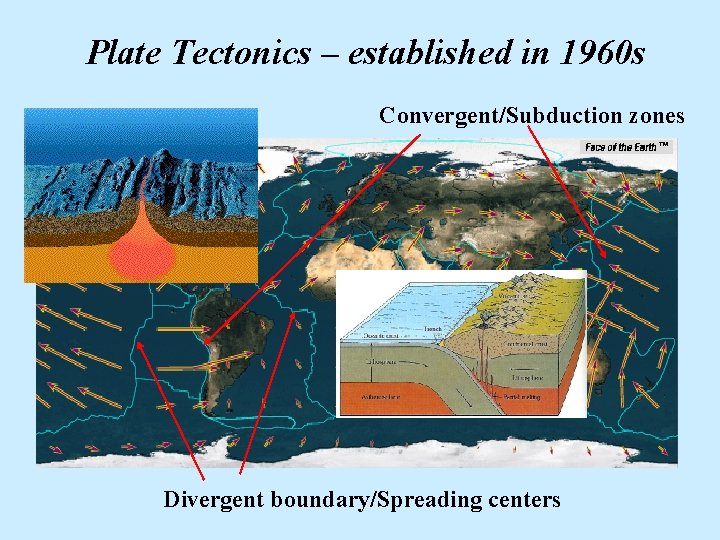
Plate Tectonics – established in 1960 s Convergent/Subduction zones Divergent boundary/Spreading centers

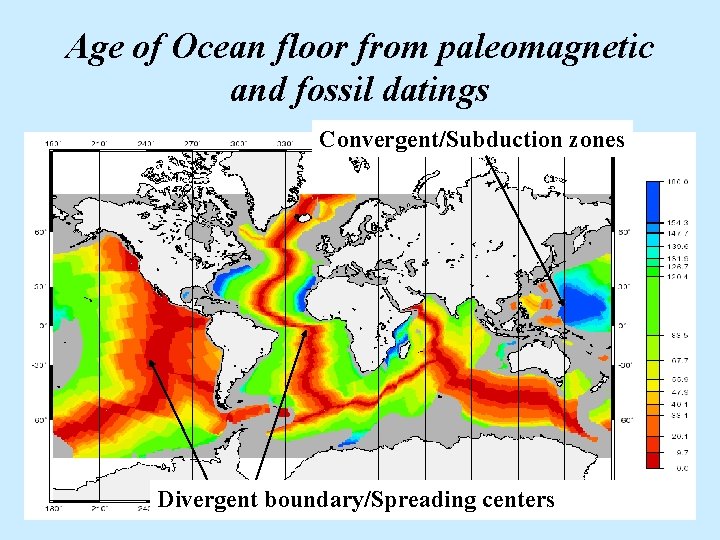
Age of Ocean floor from paleomagnetic and fossil datings Convergent/Subduction zones Divergent boundary/Spreading centers

Earth’s Surface Heat Flow Pollack et al. , 1993 Divergent boundary/Spreading centers In comparison, solar radiation to the Earth’s surface is ~1300 W/m 2.

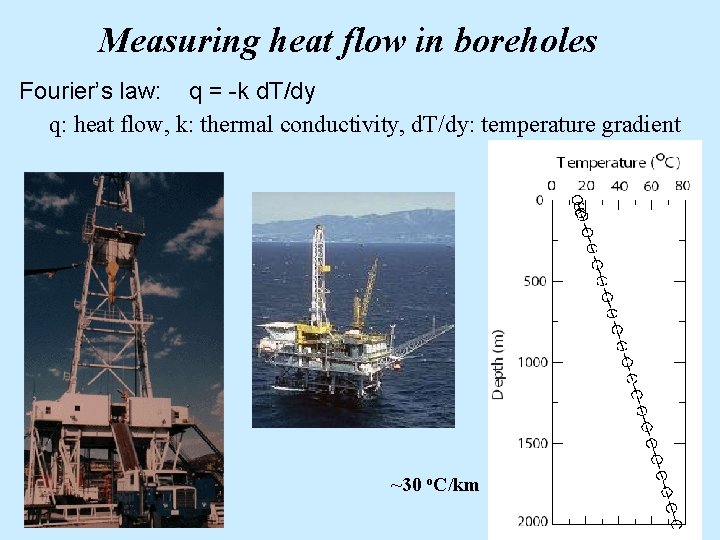
Measuring heat flow in boreholes Fourier’s law: q = -k d. T/dy q: heat flow, k: thermal conductivity, d. T/dy: temperature gradient ~30 o. C/km

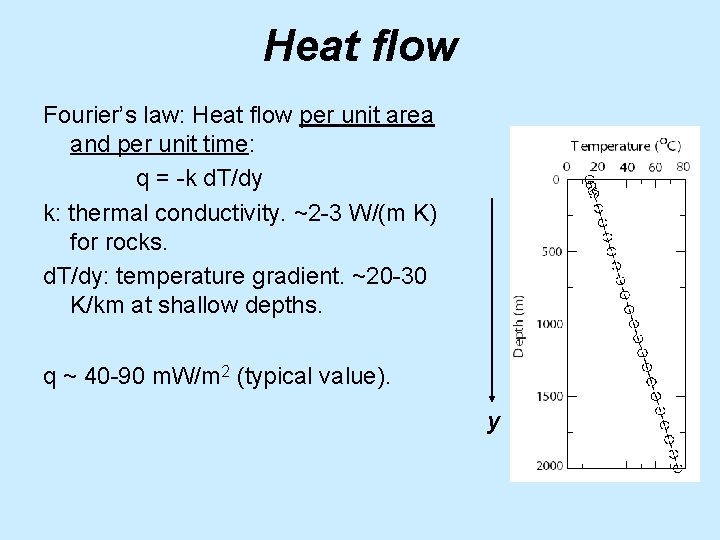
Heat flow Fourier’s law: Heat flow per unit area and per unit time: q = -k d. T/dy k: thermal conductivity. ~2 -3 W/(m K) for rocks. d. T/dy: temperature gradient. ~20 -30 K/km at shallow depths. q ~ 40 -90 m. W/m 2 (typical value). y

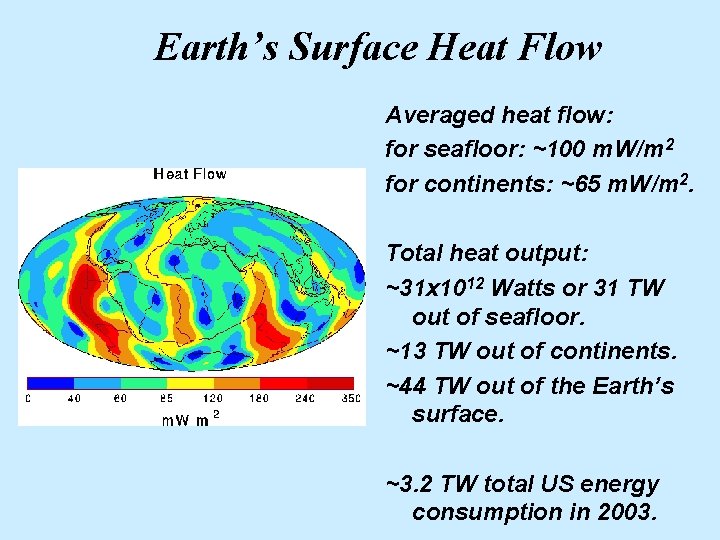
Earth’s Surface Heat Flow Averaged heat flow: for seafloor: ~100 m. W/m 2 for continents: ~65 m. W/m 2. Total heat output: ~31 x 1012 Watts or 31 TW out of seafloor. ~13 TW out of continents. ~44 TW out of the Earth’s surface. ~3. 2 TW total US energy consumption in 2003.

Heat sources Radioactive decay of 235 U, 238 U, 232 Th and 40 K Their distribution in the Earth is non-uniform. For example, their concentration is very high within the continental crust, but probably almost nonexistent in the core. Produce geo-neutrinos. Secular cooling. Significant (but unknown) amount of 44 TW surface heat flux is from the secular cooling of the Earth (e. g. , ~100 K/Gyr for the Earth’s mantle). Earth started hot, due to gravitational potential energy release in the differentiation process.

Kelvin’s [1844] (under)estimate of Earth’s age With heat conduction, T(y, t) is governed by conservation of energy: T= Tmerf[y/(4 kt)1/2]. Surface heat flux: q=kd. T/dy|y=0=k. Tm/(pkt)1/2, where k is thermal conductivity, and (pkt)1/2~d is thermal boundary layer thickness.

Kelvin’s [1844] (under)estimate of Earth’s age Taking q=qo as the present-day heat flux, Kelvin got the age of the Earth t as t=k 2 Tm 2/(pkqo 2). t~24 Myr, using the measured values of relevant parameters, which was much smaller than what geologists believed at the time, which was “nan” (not a number), until Holmes invented U-Pb radiometric dating [1911] and determined t~4. 5 Ga [1940 s].

What’s wrong with Kelvin’s estimate? Perry’s [1895] critique Perry [1895] indicated that cooling of the Earth’s interior (below the boundary layer) could provide the energy source to sustain the observed present-day heat flux for a much older Earth, and that, if the interior is fluid-like, convection could cool the interior efficiently. With no theory of convection, Perry [1895] used a high quasiconductivity to represent convection.

Mantle convection A physical process in a planetary mantle that controls the heat release from and structure formation within the mantle, thus determining the evolution of planets and their geology and tectonics. The basic theory consists of the conservation laws of mass, momentum and energy, considering the mantle as viscous flow [e. g. , Mc. Kenzie et al. , 1974]. Navier-Stokes’ equation Both convective and conductive heat transfer

Mantle convection An equation of state (i. e. , thermal expansion): Non-dimensional equations: where Ra is Rayleigh number: Ra is the ratio of convective driving force to resisting force and determines the vigor of convection (Ra~107 -108 for present-day Earth’s mantle).

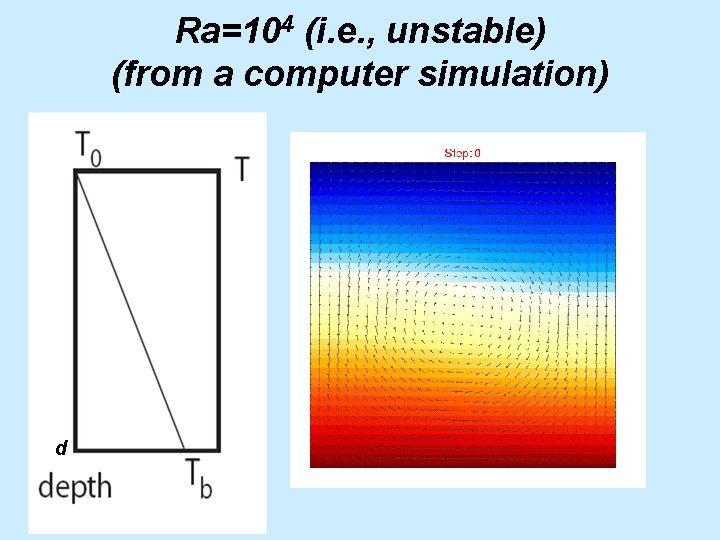
Ra=104 (i. e. , unstable) (from a computer simulation) d

Ra=104 (i. e. , unstable) (from a computer simulation)

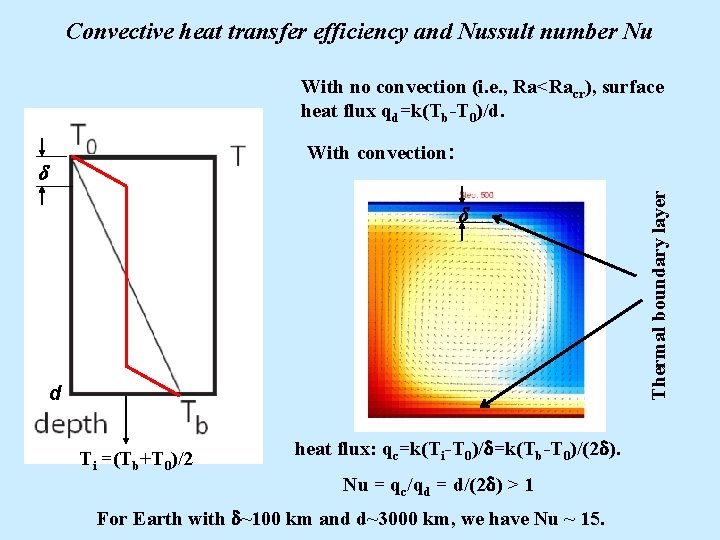
Convective heat transfer efficiency and Nussult number Nu With no convection (i. e. , Ra<Racr), surface heat flux qd=k(Tb-T 0)/d. d d d Ti =(Tb+T 0)/2 heat flux: qc=k(Ti-T 0)/d=k(Tb-T 0)/(2 d). Nu = qc/qd = d/(2 d) > 1 For Earth with d~100 km and d~3000 km, we have Nu ~ 15. Thermal boundary layer With convection:

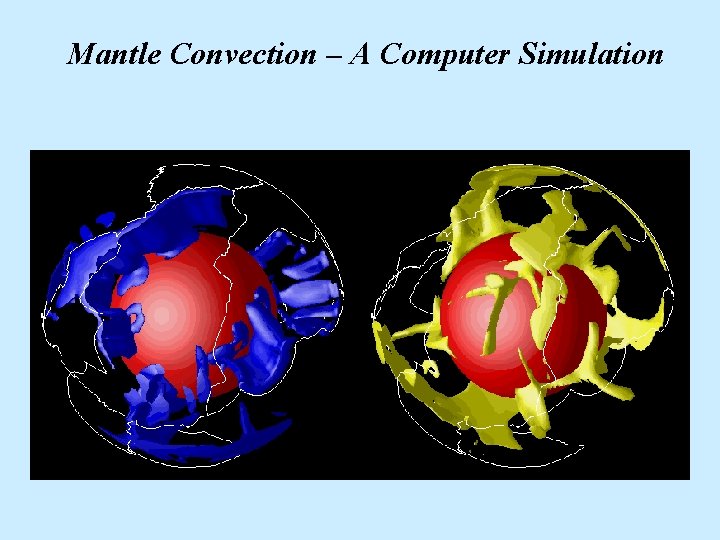
Mantle Convection – A Computer Simulation

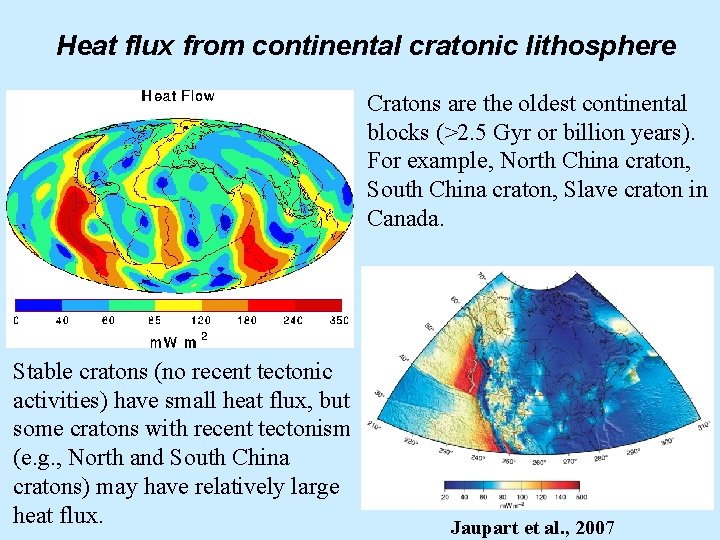
Heat flux from continental cratonic lithosphere Cratons are the oldest continental blocks (>2. 5 Gyr or billion years). For example, North China craton, South China craton, Slave craton in Canada. Stable cratons (no recent tectonic activities) have small heat flux, but some cratons with recent tectonism (e. g. , North and South China cratons) may have relatively large heat flux. Jaupart et al. , 2007

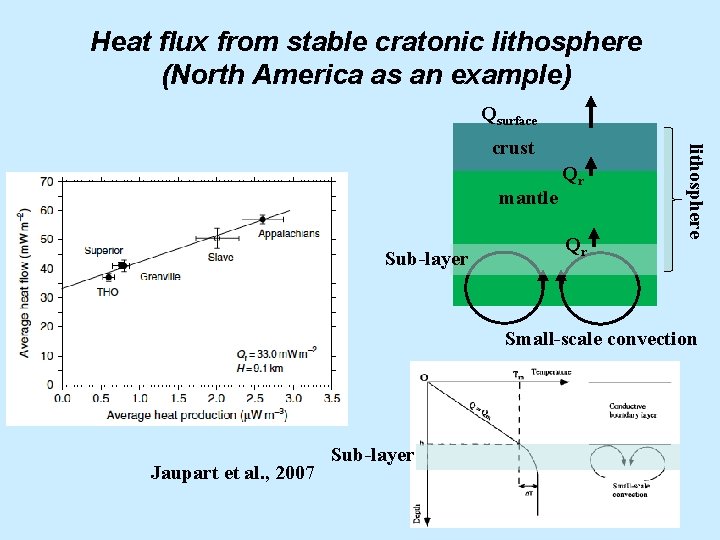
Heat flux from stable cratonic lithosphere (North America as an example) Qsurface mantle Sub-layer Qr Qr lithosphere crust Small-scale convection Jaupart et al. , 2007 Sub-layer

Why does small-scale convection occur with the sub-layer? Sub-layer It’s all because the sub-layer is at the bottom of lithosphere. 1) The sub-layer remains negatively buoyant (unlike the well-mixed mantle below), and is gravitationally unstable – providing the driving force for convection. 2) The sub-layer is not too viscous (unlike the conductive boundary layer above), and it can still deform and participate in the convection. Davaille & Jaupart [1994] developed a theory for the heat flux based on their fluid dynamics experiments. where DTv is convective temperature scale that depends on interior temperature Tm and viscosity m as a function of temperature.

Small-scale convection from 2 D Models (Huang et al. , 2003)

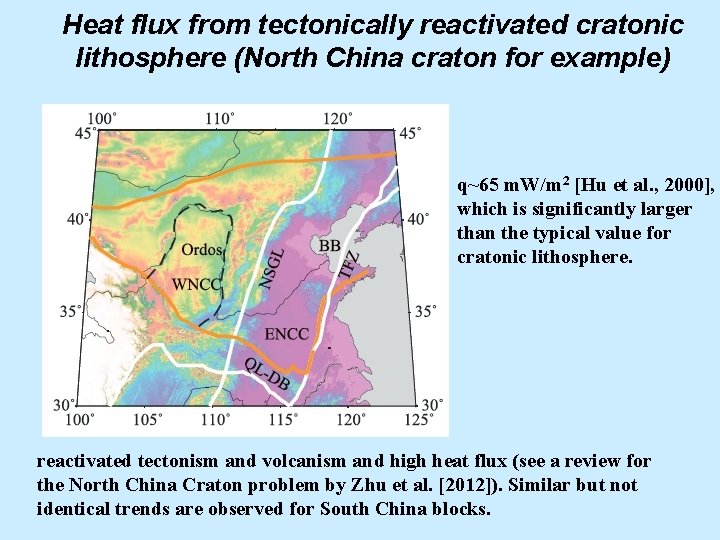
Heat flux from tectonically reactivated cratonic lithosphere (North China craton for example) q~65 m. W/m 2 [Hu et al. , 2000], which is significantly larger than the typical value for cratonic lithosphere. reactivated tectonism and volcanism and high heat flux (see a review for the North China Craton problem by Zhu et al. [2012]). Similar but not identical trends are observed for South China blocks.

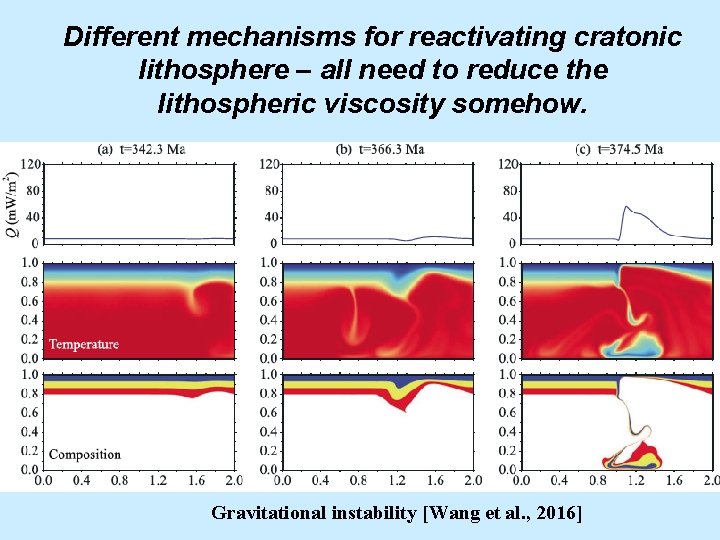
Different mechanisms for reactivating cratonic lithosphere – all need to reduce the lithospheric viscosity somehow. Gravitational instability [Wang et al. , 2016]

Concluding remarks • Convective heat flux into the stable continental lithosphere is controlled with small-scale convection involved the lithospheric sub-layer. Some wellestablished theory has been established. • Convective heat flux into the reactivated continental lithosphere such as North China and South China cratons can be significantly larger, and relevant mechanisms remain in debate. • On both regional scales (e. g. , near JUNO site or South China craton) and global scale, it is important to distinguish the contributions from radiogenic and non-radiogenic heating sources. This is where geo-neutrino studies are needed.