Manipulating a Classical Electron Haruka Maeda Donald Norum

Manipulating a Classical Electron Haruka Maeda Donald Norum Joshua Gurian University of Virginia

Making and manipulating a classical Rydberg atom Li+

Outline Motivation: making “classical” atoms which last more than a few orbits Manipulating these atoms in “classical” and non classical ways Quantum mechanical description Potential applications

Rydberg Atom An atom in a state of high principal quantum number n W= -1/2 n 2 <r>=n 2 V=-1/r Large, weakly bound orbits n=30 <r>= 900 a 0 μ =900 ea 0 W =-120 cm-1

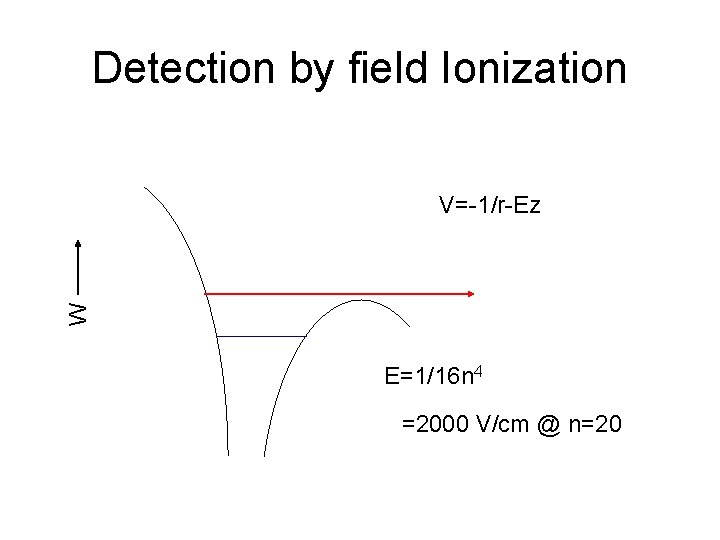
Detection by field Ionization W V=-1/r-Ez E=1/16 n 4 =2000 V/cm @ n=20

The Classical Rydberg atom The electron is moving; its not a stationary probability distribution. Quantum Approximation: the Rydberg wavepacket, a coherent superposition of Rydberg states (multilevel quantum beats, motion at beat frequency) First realization: Stroud, Yeazell, Noel, Rochester Van Linden van den Heuvell, Muller, Noordam, FOM The problem: the wave packets do not last very long, tens of orbits, 100 ps Why not?

Dispersion, the level spacings are not the same, the beat frequencies get out of phase. At n=60 the dispersion is 3/n or 5% per state. A wavepacket containing five states lasts about five orbits. Dephasing, the coherence between the states is lost→ a stationary probability distribution. Sources- stray fields, collisions

How can we make the wavepacket last for many orbits? Add a weak field oscillating synchronously with the orbit Proposals Circularly polarized microwaves Bialynicki-Birula, Kalinsky, and Eberly Farrelly and Uzer Linearly polarized microwaves Buchleitner and Delande Trains of half cycle pulses Reinhold and Burgdorfer realization by Dunning Such wavepackets are called non dispersing wavepackets.

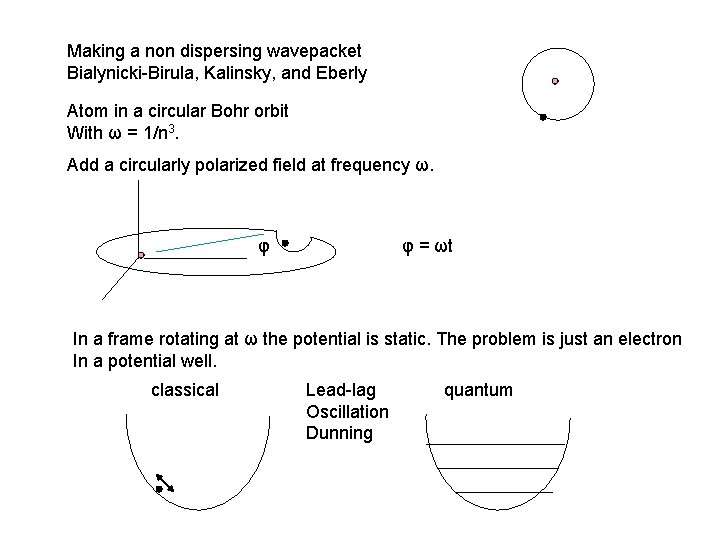
Making a non dispersing wavepacket Bialynicki-Birula, Kalinsky, and Eberly Atom in a circular Bohr orbit With ω = 1/n 3. Add a circularly polarized field at frequency ω. φ φ = ωt In a frame rotating at ω the potential is static. The problem is just an electron In a potential well. classical Lead-lag Oscillation Dunning quantum

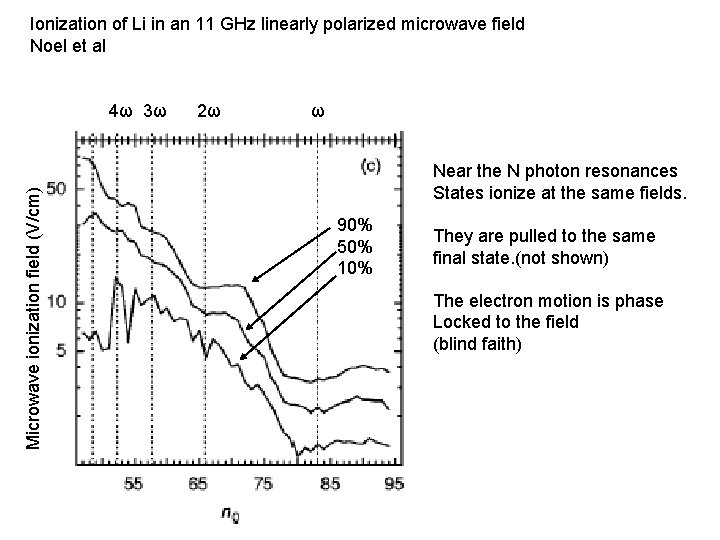
Ionization of Li in an 11 GHz linearly polarized microwave field Noel et al Microwave ionization field (V/cm) 4ω 3ω 2ω ω Near the N photon resonances States ionize at the same fields. 90% 50% 10% They are pulled to the same final state. (not shown) The electron motion is phase Locked to the field (blind faith)

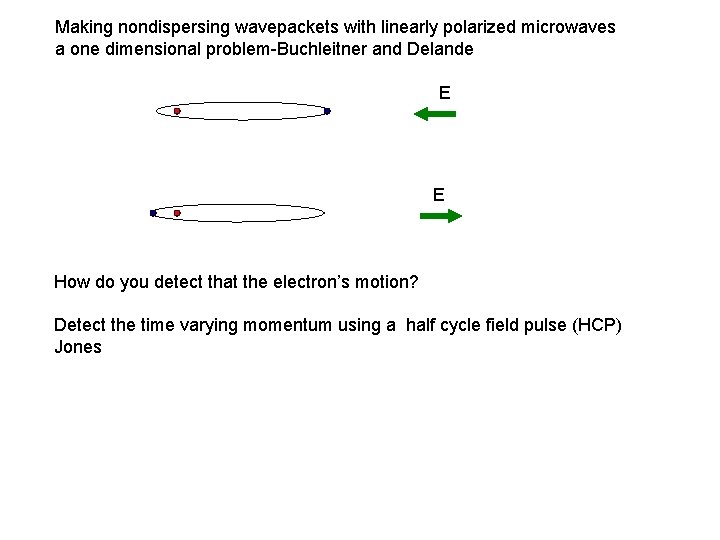
Making nondispersing wavepackets with linearly polarized microwaves a one dimensional problem-Buchleitner and Delande E E How do you detect that the electron’s motion? Detect the time varying momentum using a half cycle field pulse (HCP) Jones

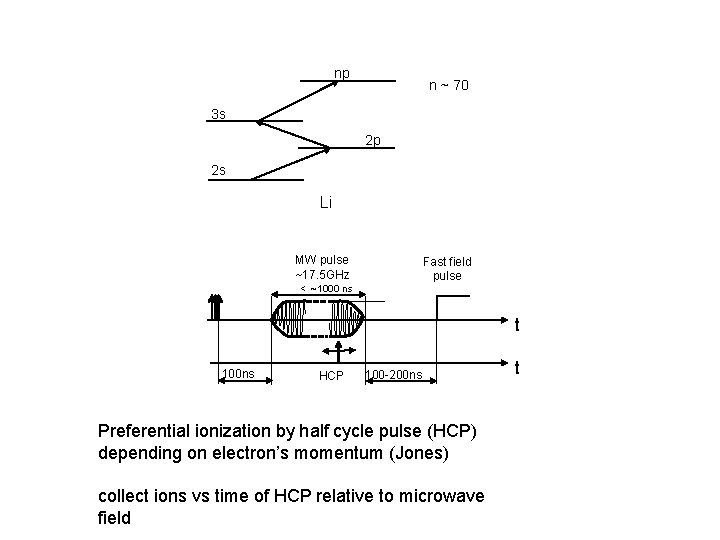
Time Resolved Momentum Analysis-Jones For Tpulse << T Kepler ∆p For an initial momentum p 0 Set ∆p for 50% ionization of an eigenstate (it just ionizes at a turning point). The atom ionizes in the lower half orbit.

np n ~ 70 3 s 2 p 2 s Li MW pulse ~17. 5 GHz Fast field pulse < ~1000 ns t 100 ns HCP 100 -200 ns Preferential ionization by half cycle pulse (HCP) depending on electron’s momentum (Jones) collect ions vs time of HCP relative to microwave field t

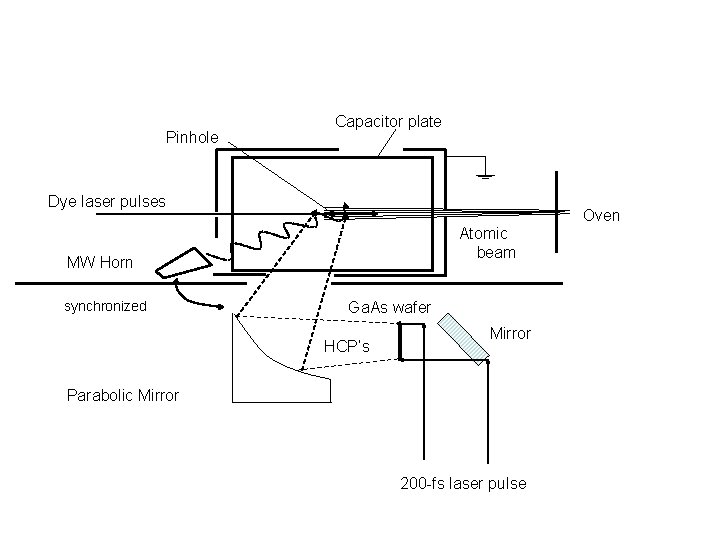
Pinhole Capacitor plate Dye laser pulses Oven Atomic beam MW Horn synchronized Ga. As wafer HCP’s Mirror Parabolic Mirror 200 -fs laser pulse

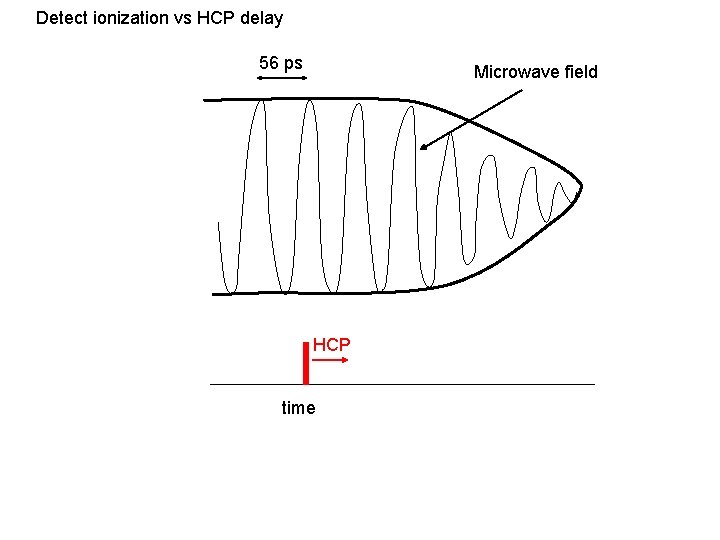
Detect ionization vs HCP delay 56 ps Microwave field HCP time

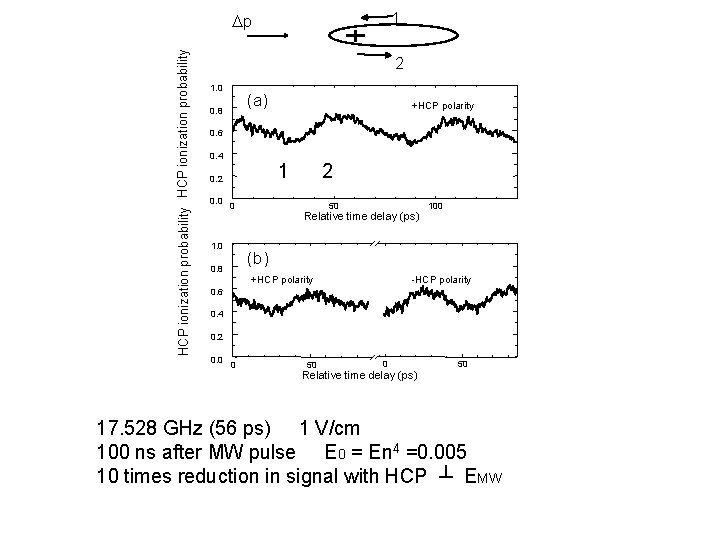
1 HCP ionization probability Dp 2 1. 0 (a) 0. 8 +HCP polarity 0. 6 0. 4 1 0. 2 0. 0 0 1. 0 2 50 Relative time delay (ps) 100 (b) 0. 8 +HCP polarity -HCP polarity 0. 6 0. 4 0. 2 0. 0 0 50 Relative time delay (ps) 17. 528 GHz (56 ps) 1 V/cm 100 ns after MW pulse E 0 = En 4 =0. 005 10 times reduction in signal with HCP ┴ EMW

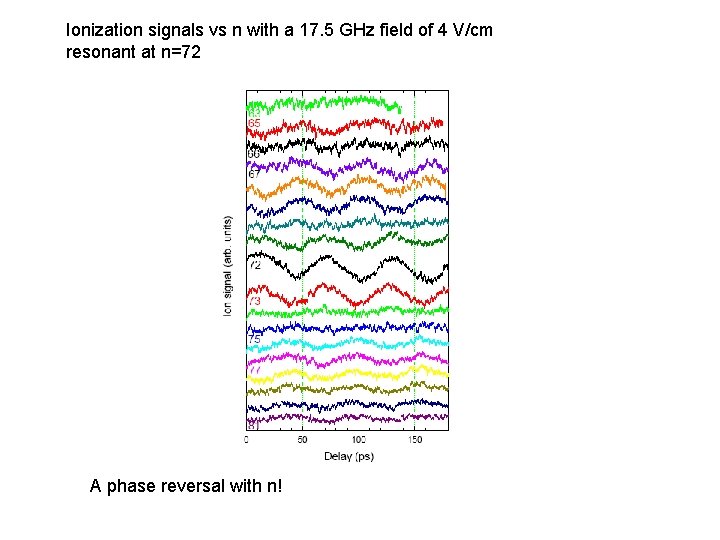
Ionization signals vs n with a 17. 5 GHz field of 4 V/cm resonant at n=72 A phase reversal with n!

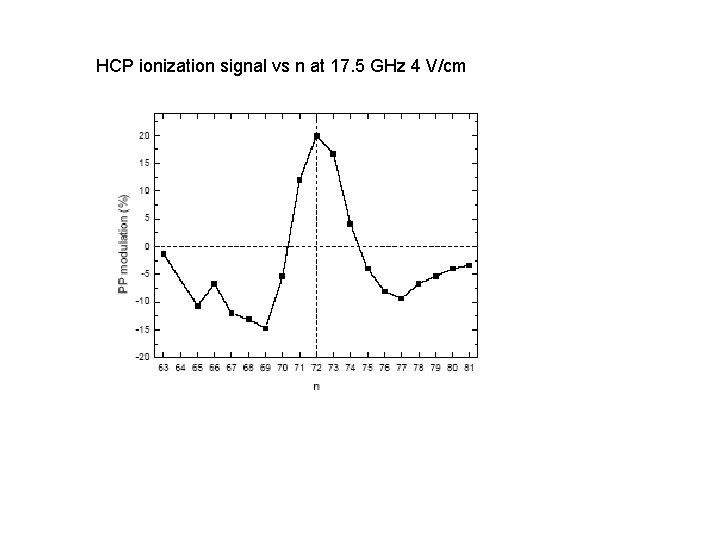
HCP ionization signal vs n at 17. 5 GHz 4 V/cm

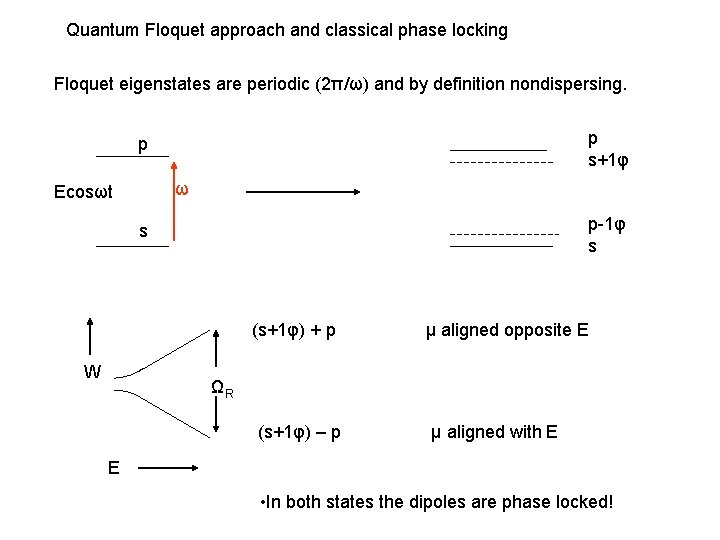
Quantum Floquet approach and classical phase locking Floquet eigenstates are periodic (2π/ω) and by definition nondispersing. p s+1φ p ω Ecosωt p-1φ s s (s+1φ) + p W μ aligned opposite E ΩR (s+1φ) – p μ aligned with E E • In both states the dipoles are phase locked!

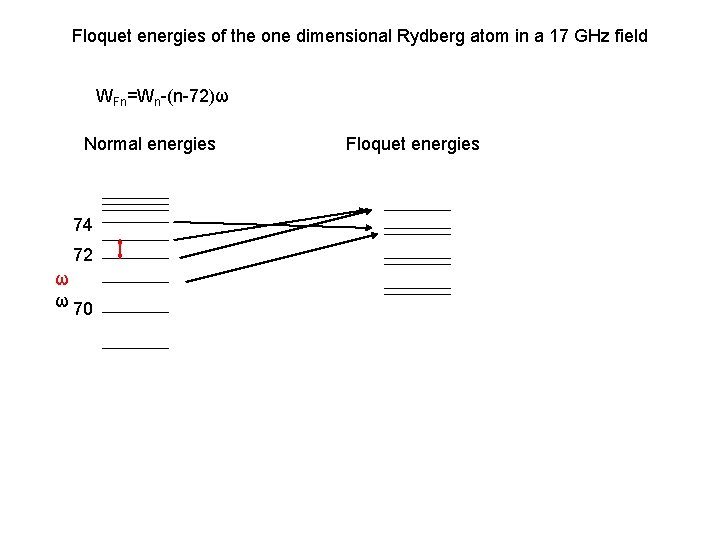
Floquet energies of the one dimensional Rydberg atom in a 17 GHz field WFn=Wn-(n-72)ω Normal energies 74 72 ω ω 70 Floquet energies

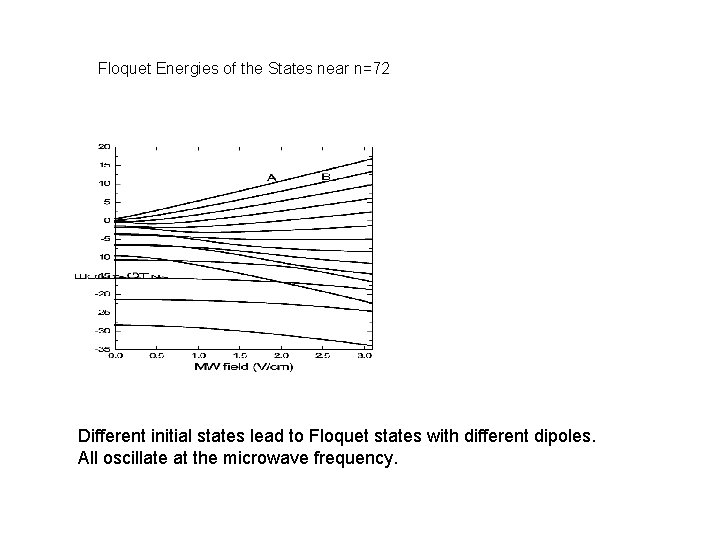
Floquet Energies of the States near n=72 Different initial states lead to Floquet states with different dipoles. All oscillate at the microwave frequency.

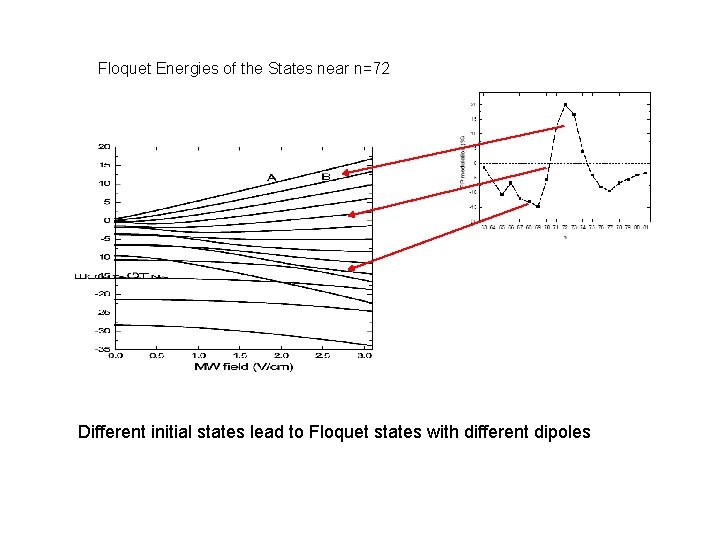
Floquet Energies of the States near n=72 Different initial states lead to Floquet states with different dipoles

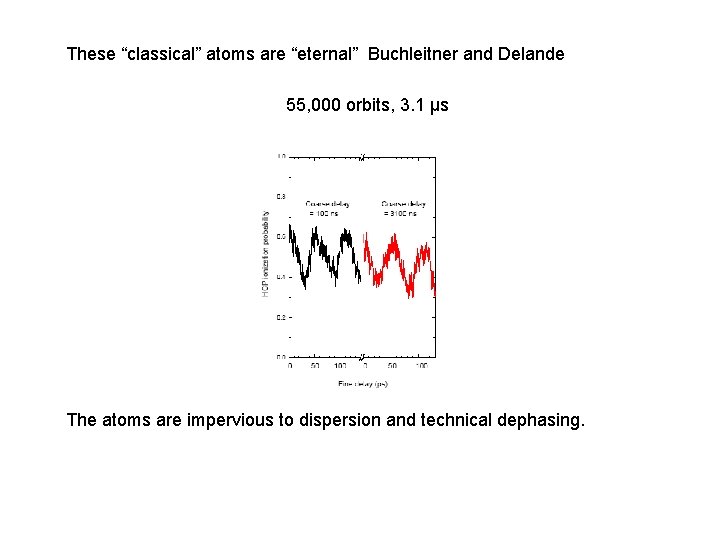
These “classical” atoms are “eternal” Buchleitner and Delande 55, 000 orbits, 3. 1 μs The atoms are impervious to dispersion and technical dephasing.

Elimination of Technical Dephasing The electron is phase locked to the 17 GHz field. It’s localized in a potential well in the 17 GHz frame. Low frequency noise averages to zero in this frame.

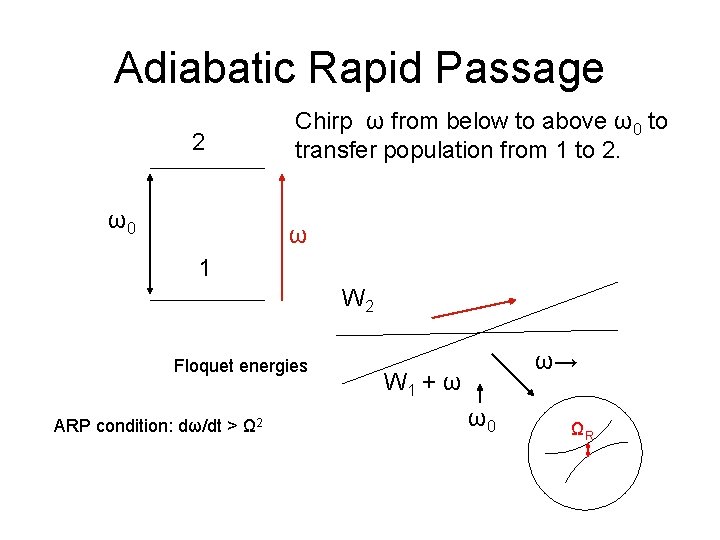
If the electron is phase locked to the microwave field, can we speed it up or slow it down by chirping the microwave frequency ω? first suggested by Kalinski and Eberly Application to molecules Villeneuve et al Since ω =1/n 3, this amounts to changing n or the binding energy.

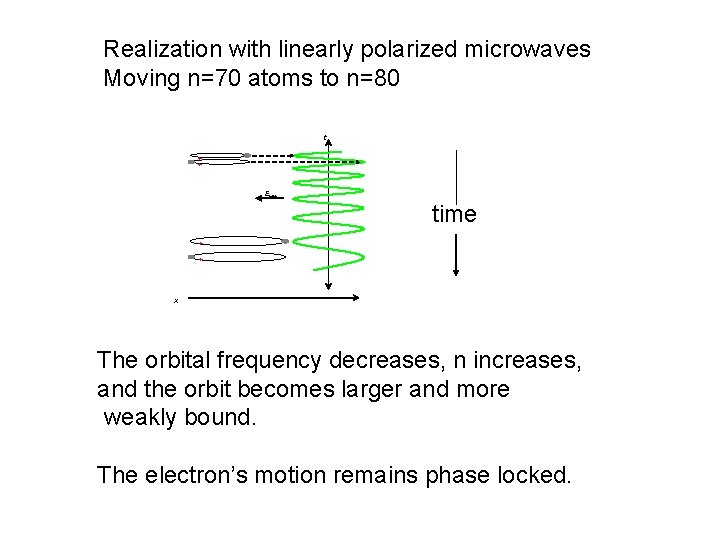
Realization with linearly polarized microwaves Moving n=70 atoms to n=80 t + + EMW time + + x The orbital frequency decreases, n increases, and the orbit becomes larger and more weakly bound. The electron’s motion remains phase locked.

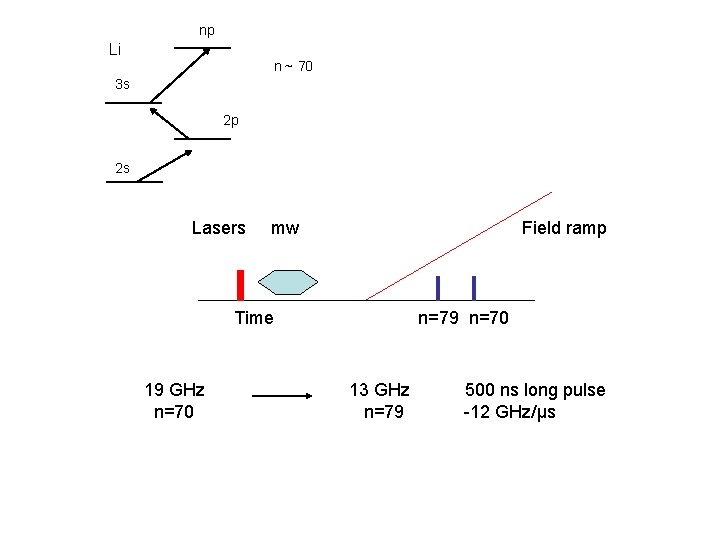
np Li n ~ 70 3 s 2 p 2 s Lasers mw Field ramp Time 19 GHz n=70 n=79 n=70 13 GHz n=79 500 ns long pulse -12 GHz/μs

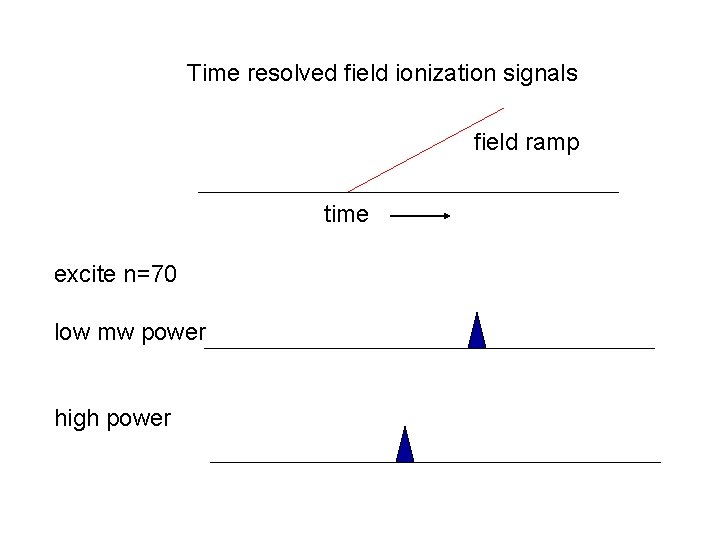
Time resolved field ionization signals field ramp time excite n=70 low mw power high power

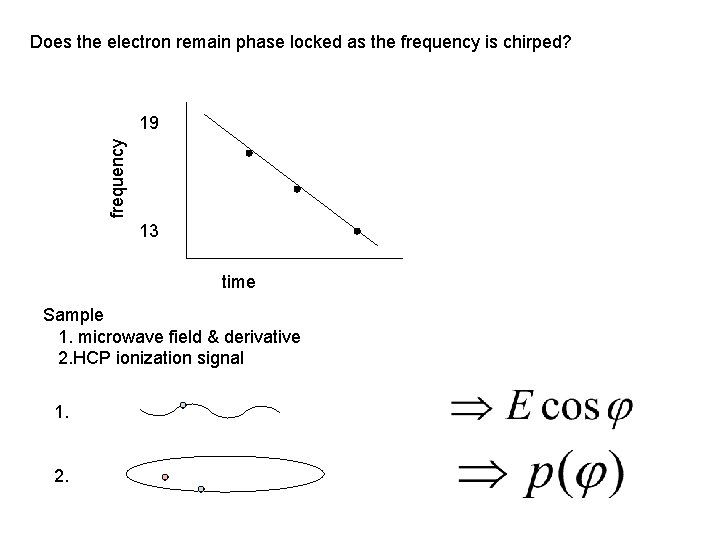
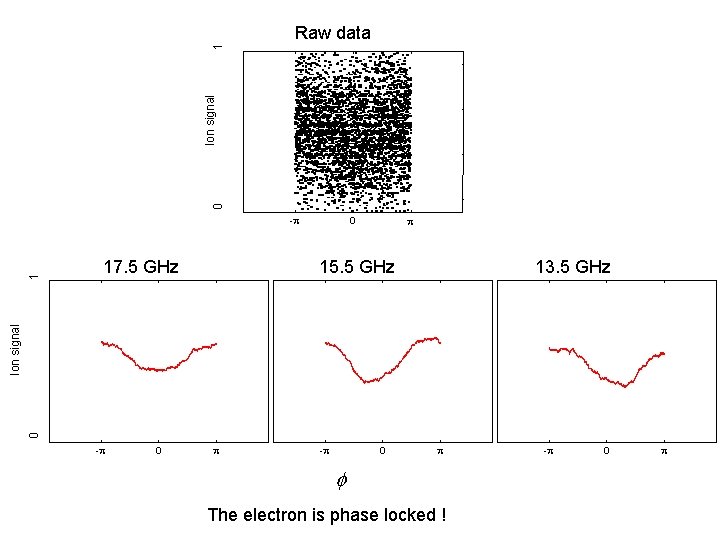
Does the electron remain phase locked as the frequency is chirped? frequency 19 13 time Sample 1. microwave field & derivative 2. HCP ionization signal 1. 2.

0 Ion signal 1 Raw data 1 15. 5 GHz 13. 5 GHz 0 Ion signal 17. 5 GHz p 0 -p -p 0 p f The electron is phase locked ! -p 0 p

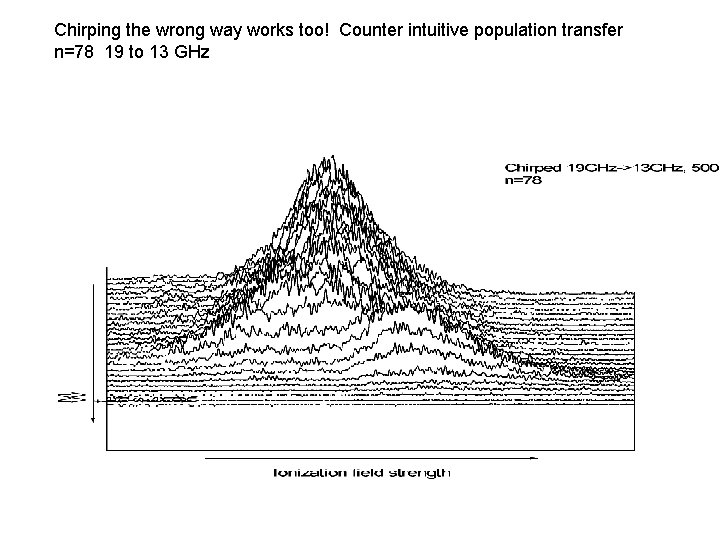
Chirping the wrong way works too! Counter intuitive population transfer n=78 19 to 13 GHz

Quantum mechanical population transfer from n=72 to n=82 Chirping from 19 to 13 GHz is a sequence of single photon adiabatic passages

Adiabatic Rapid Passage 2 ω0 Chirp ω from below to above ω0 to transfer population from 1 to 2. ω 1 W 2 Floquet energies ARP condition: dω/dt > Ω 2 ω→ W 1 + ω ω0 ΩR

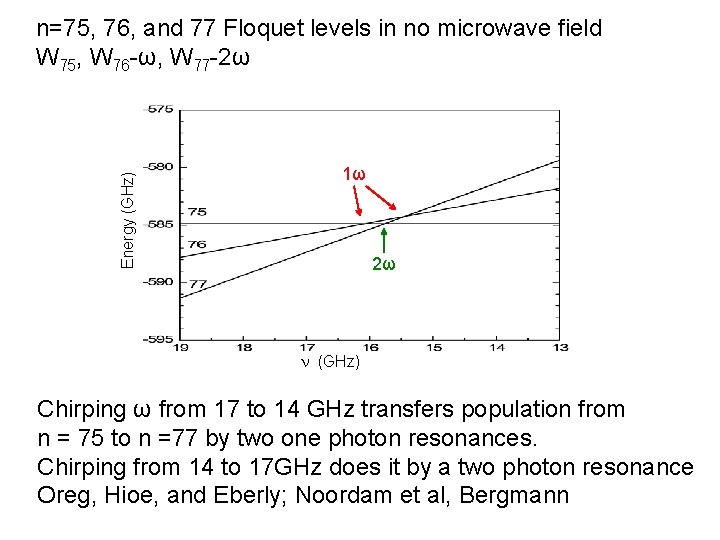
Energy (GHz) n=75, 76, and 77 Floquet levels in no microwave field W 75, W 76 -ω, W 77 -2ω 1ω 2ω n (GHz) Chirping ω from 17 to 14 GHz transfers population from n = 75 to n =77 by two one photon resonances. Chirping from 14 to 17 GHz does it by a two photon resonance Oreg, Hioe, and Eberly; Noordam et al, Bergmann

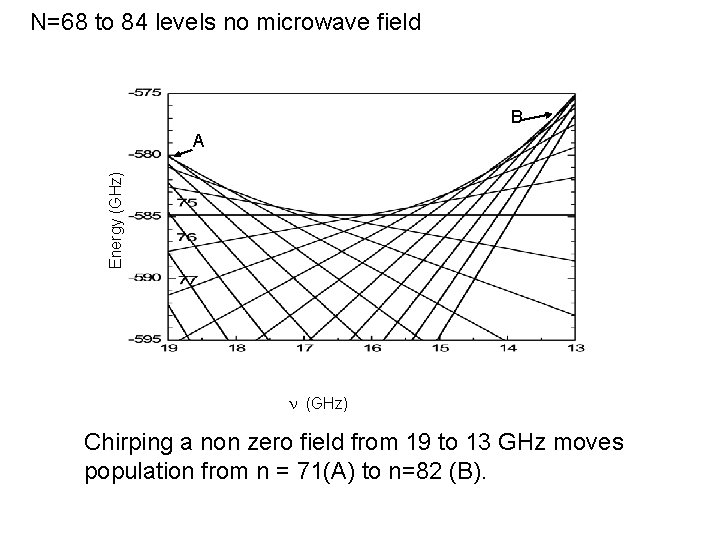
N=68 to 84 levels no microwave field B Energy (GHz) A n (GHz) Chirping a non zero field from 19 to 13 GHz moves population from n = 71(A) to n=82 (B).

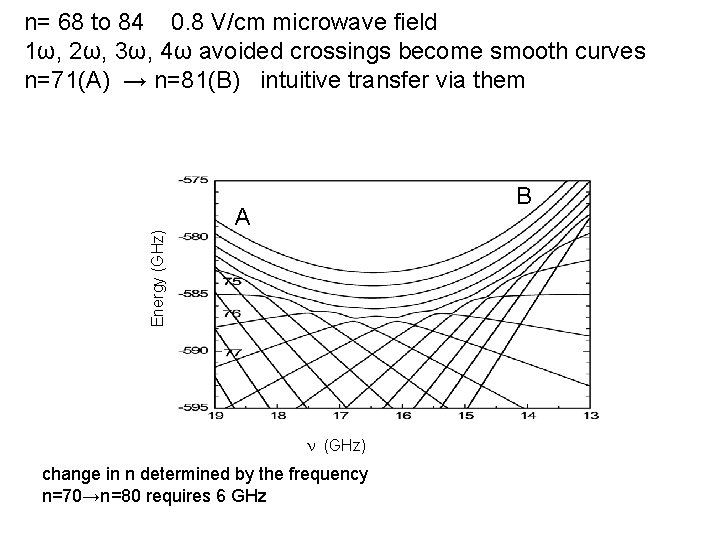
Energy (GHz) n= 68 to 84 0. 8 V/cm microwave field 1ω, 2ω, 3ω, 4ω avoided crossings become smooth curves n=71(A) → n=81(B) intuitive transfer via them B A n (GHz) change in n determined by the frequency n=70→n=80 requires 6 GHz

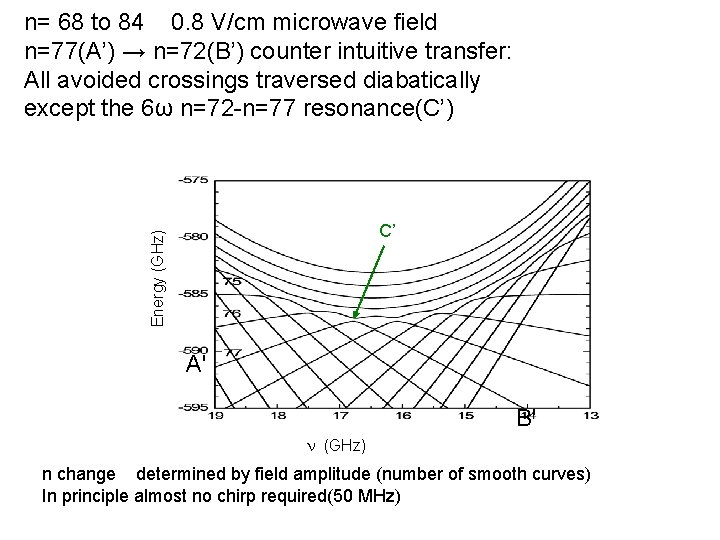
n= 68 to 84 0. 8 V/cm microwave field n=77(A’) → n=72(B’) counter intuitive transfer: All avoided crossings traversed diabatically except the 6ω n=72 -n=77 resonance(C’) Energy (GHz) C’ A' B' n (GHz) n change determined by field amplitude (number of smooth curves) In principle almost no chirp required(50 MHz)

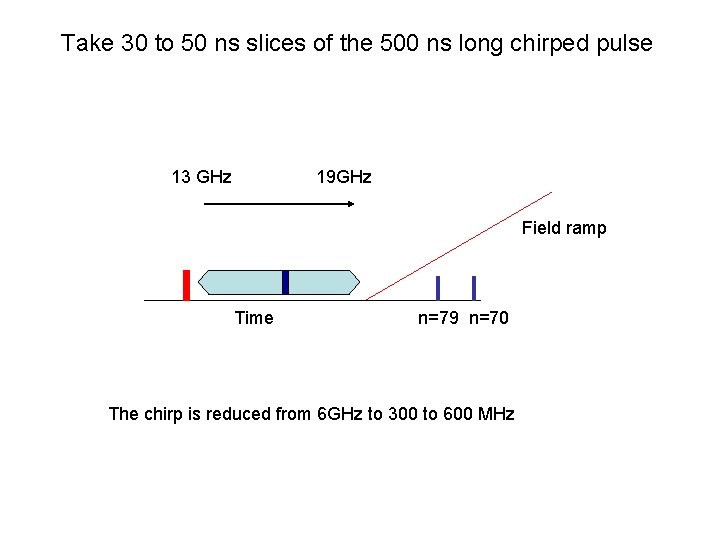
Take 30 to 50 ns slices of the 500 ns long chirped pulse 13 GHz 19 GHz Field ramp Time n=79 n=70 The chirp is reduced from 6 GHz to 300 to 600 MHz

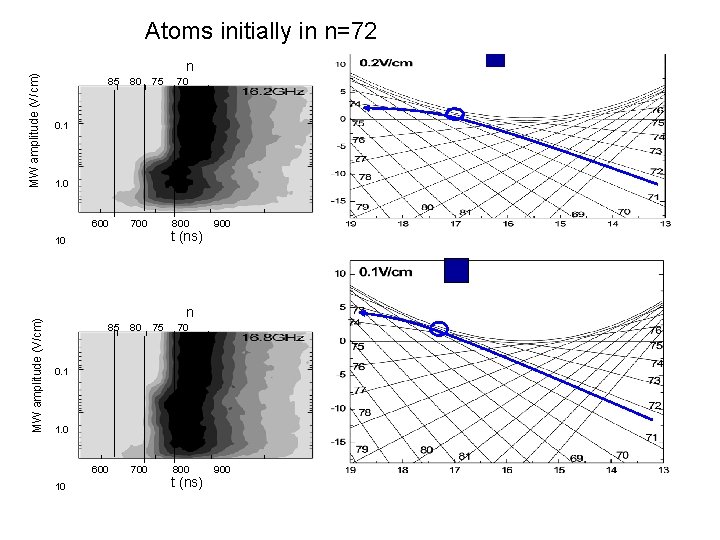
MW amplitude (V/cm) Atoms initially in n=72 n 85 80 75 0. 1 1. 0 600 700 800 t (ns) 10 MW amplitude (V/cm) 70 900 n 85 80 75 70 0. 1 1. 0 600 10 700 800 t (ns) 900

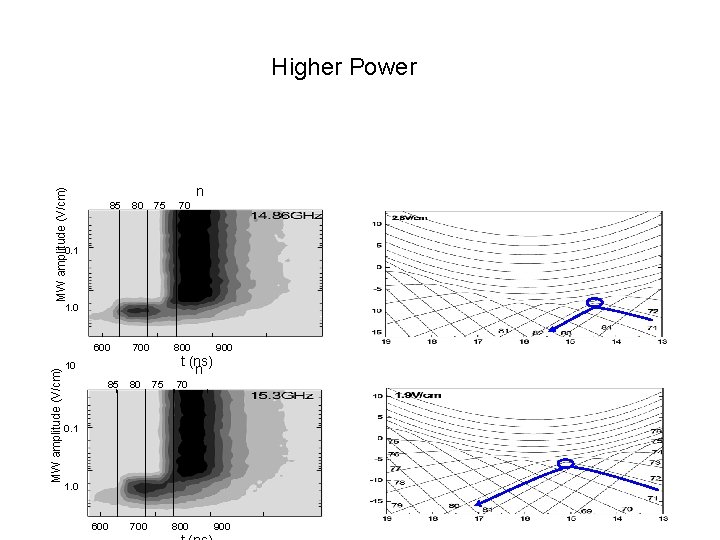
Higher Power MW amplitude (V/cm) n 85 80 75 70 0. 1 1. 0 MW amplitude (V/cm) 600 700 800 t (ns) n 10 85 80 75 900 70 0. 1 1. 0 600 700 800 900

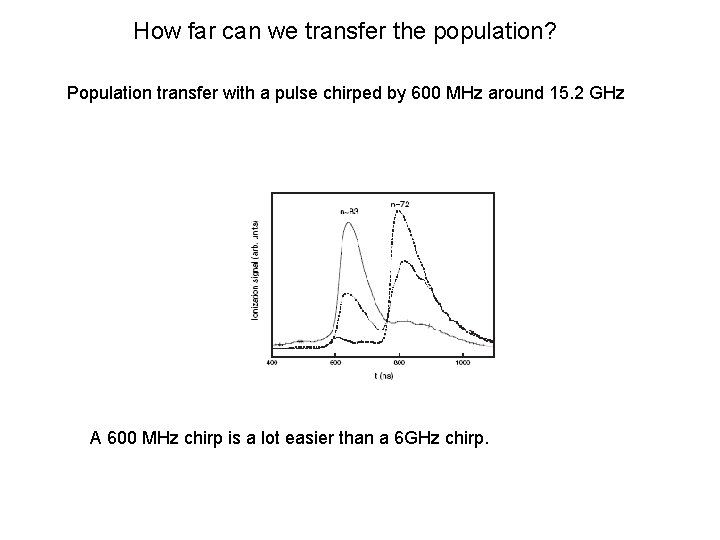
How far can we transfer the population? Population transfer with a pulse chirped by 600 MHz around 15. 2 GHz A 600 MHz chirp is a lot easier than a 6 GHz chirp.

Other Uses of these population transfer techniques Moving anti hydrogen to lower lying states Two successive counterintuitive Δn=10 transfers in 100 ns The counterintuitive, or multiphoton, process could be useful for climbing a vibrational ladder 3% instead of 30% frequency chirp

Conclusions • Non dispersing wavepackets are made by phase locking the electron’s motion to the field. • They are easy to make and live forever. • They can be manipulated to transfer population over many n states.

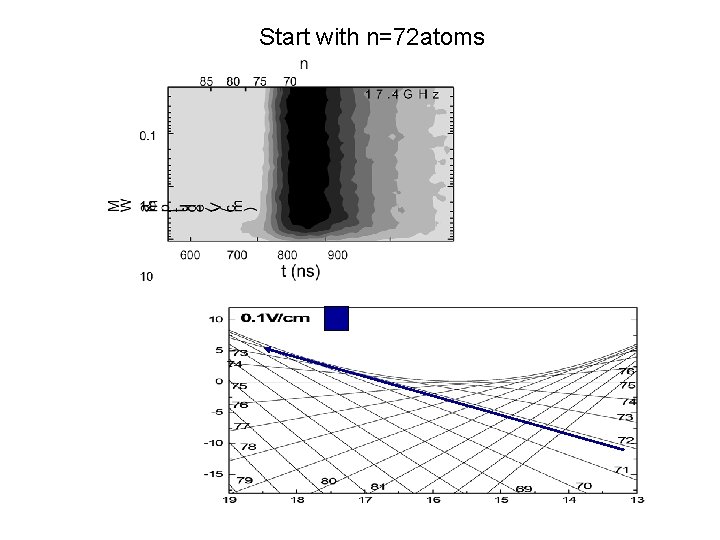
Start with n=72 atoms