Manifold Learning Bosh Shih Outline Introduction Principal Component

Manifold Learning Bosh Shih

Outline • Introduction • Principal Component Analysis (PCA) • Linear Discriminant Analysis (LDA) • Multi-Dimensional Scaling (MDS) • Isometric Feature Mapping (Isomap) • Locally Linear Embedding (LLE) • Local Discriminant Embedding (LDE) • Maximum Variance Unfolding (MVU) • Laplacian Eigenmap • Demo • summary

Introduction • Q: • complicated feature → high dimension → data (exponential growth) • the curse of dimensionality • A: • dimensionality reduction • manifold learning (one of them) Ref : 中央研究院週報 (第 1058期) 流行學習與人臉辨識

Introduction • appearance of face • goal : visualize Ref : The Manifold Ways of Perception. H. Seung and D. Lee. (2000)
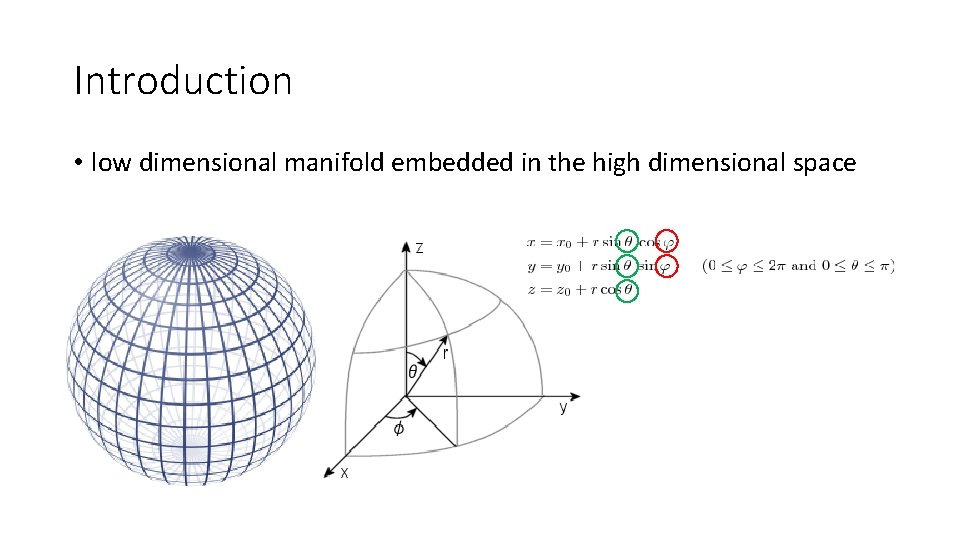
Introduction • low dimensional manifold embedded in the high dimensional space
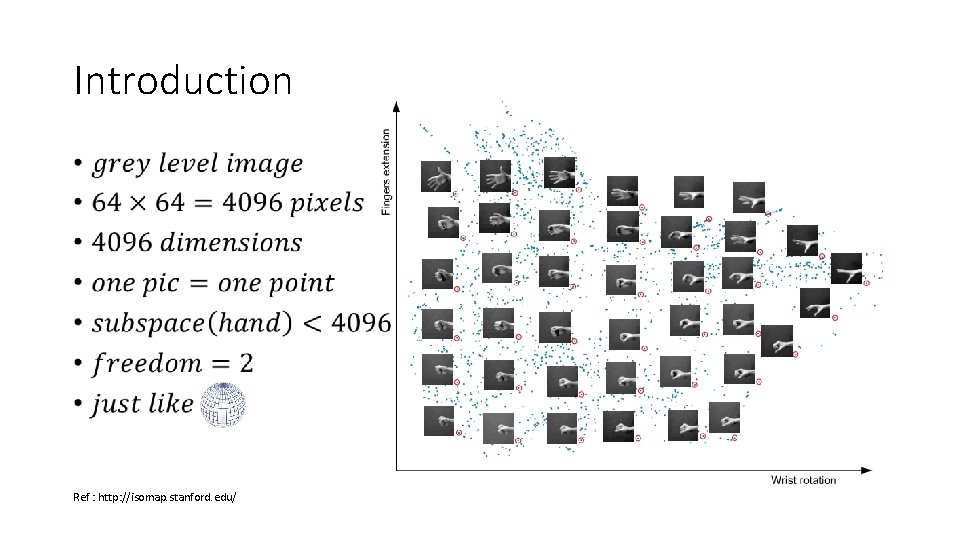
Introduction • Ref : http: //isomap. stanford. edu/
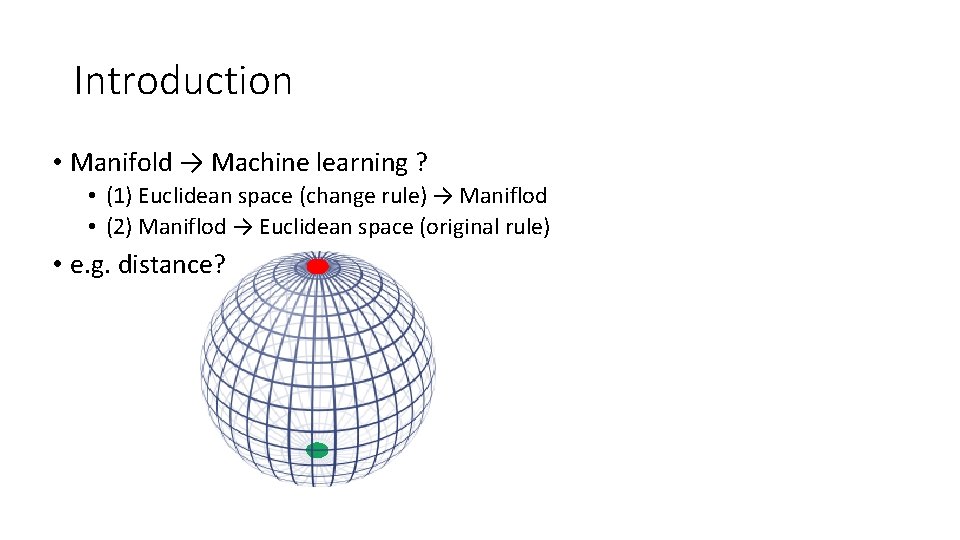
Introduction • Manifold → Machine learning ? • (1) Euclidean space (change rule) → Maniflod • (2) Maniflod → Euclidean space (original rule) • e. g. distance?

Outline • Introduction • Principal Component Analysis (PCA) • Linear Discriminant Analysis (LDA) • Multi-Dimensional Scaling (MDS) • Isometric Feature Mapping (Isomap) • Locally Linear Embedding (LLE) • Local Discriminant Embedding (LDE) • Maximum Variance Unfolding (MVU) • Laplacian Eigenmap • Demo • summary
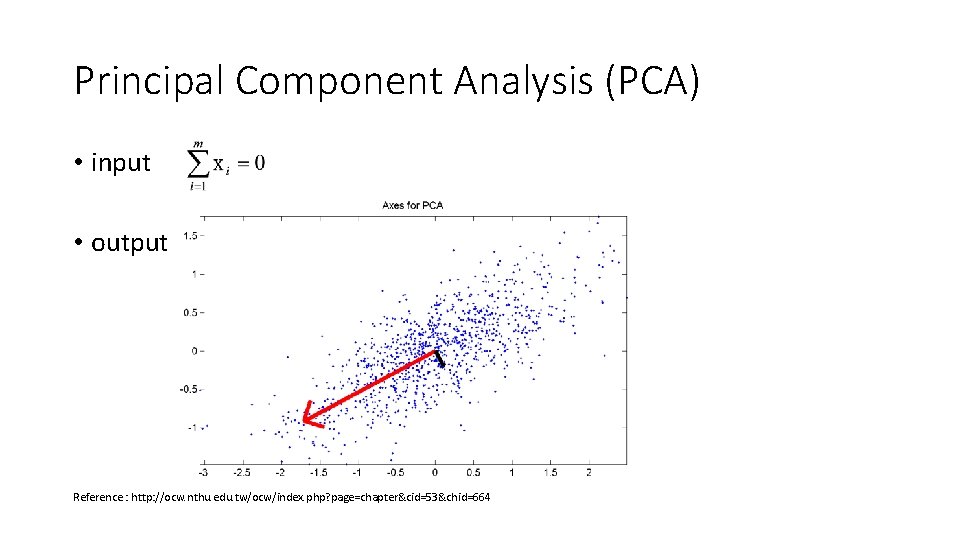
Principal Component Analysis (PCA) • input • output Reference : http: //ocw. nthu. edu. tw/ocw/index. php? page=chapter&cid=53&chid=664

Principal Component Analysis (PCA) • dataset • projection • square sum • objective function constraint • optimization Lagrange multiplier

Principal Component Analysis (PCA) • sample mean • covariance matrix • eigenvalues eigenvectors • transformation
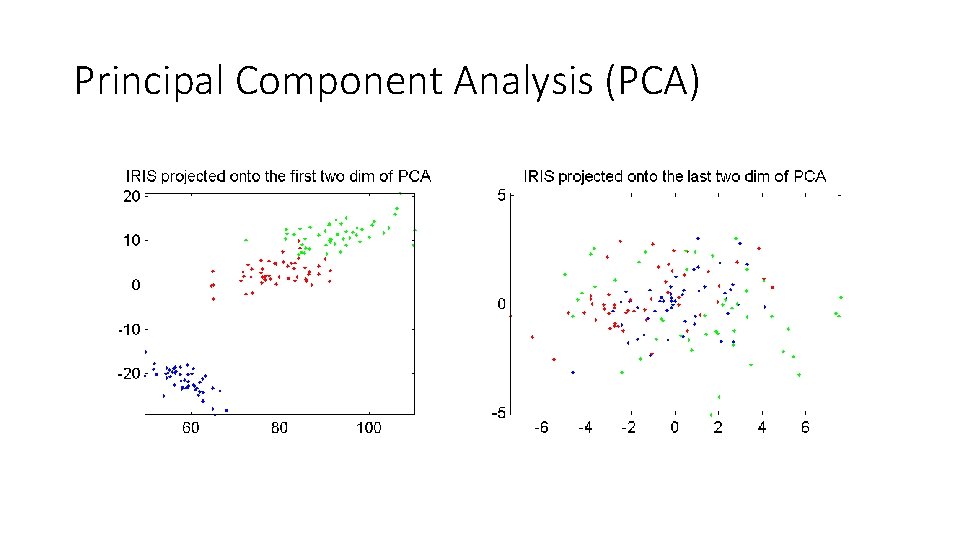
Principal Component Analysis (PCA)
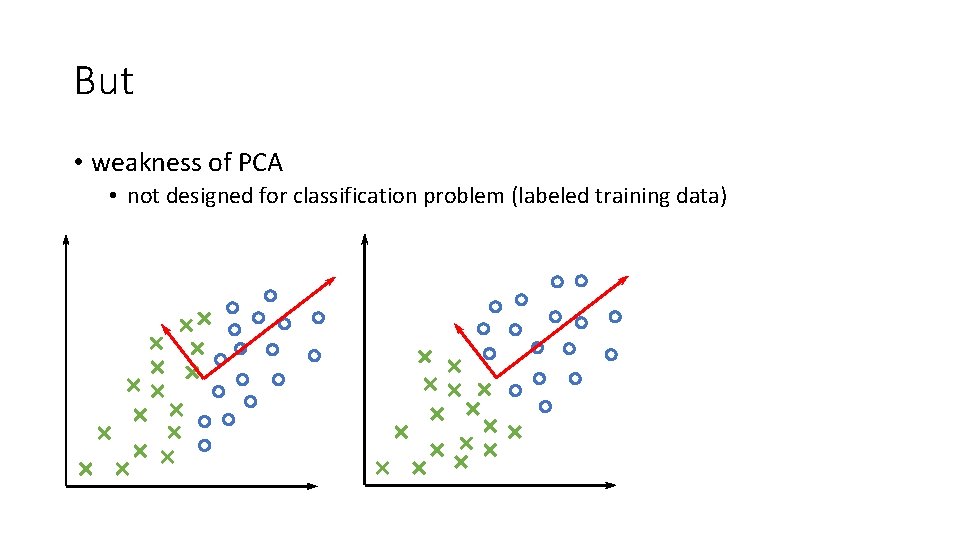
But • weakness of PCA • not designed for classification problem (labeled training data)

Outline • Introduction • Principal Component Analysis (PCA) • Linear Discriminant Analysis (LDA) • Multi-Dimensional Scaling (MDS) • Isometric Feature Mapping (Isomap) • Locally Linear Embedding (LLE) • Local Discriminant Embedding (LDE) • Maximum Variance Unfolding (MVU) • Laplacian Eigenmap • Demo • summary
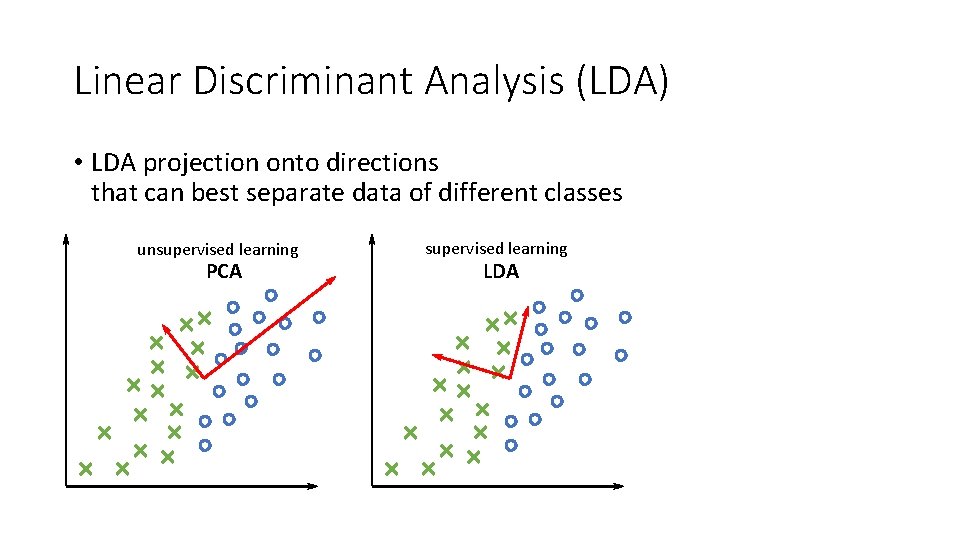
Linear Discriminant Analysis (LDA) • LDA projection onto directions that can best separate data of different classes unsupervised learning PCA supervised learning LDA

Linear Discriminant Analysis (LDA) • Reference : http: //www. cnblogs. com/Left. Not. Easy/archive/2011/01/08/lda-and-pca-machine-learning. html

Linear Discriminant Analysis (LDA) lagrange multiplier

Linear Discriminant Analysis (LDA) • multiclass

Outline • Introduction • Principal Component Analysis (PCA) • Linear Discriminant Analysis (LDA) • Multi-Dimensional Scaling (MDS) • Isometric Feature Mapping (Isomap) • Locally Linear Embedding (LLE) • Local Discriminant Embedding (LDE) • Maximum Variance Unfolding (MVU) • Laplacian Eigenmap • Demo • summary

Multi-Dimensional Scaling (MDS) • Reference : Modern Multidimensional Scaling: theory and applications(2005) https: //ccjou. wordpress. com/2013/05/29/%E 5%8 F%A 4%E 5%85%B 8%E 5%A 4%9 A%E 7%B 6%AD%E 6%A 8%99%E 5%BA%A 6%E 6%B 3%95 -mds/

Multi-Dimensional Scaling (MDS) cost function

Multi-Dimensional Scaling (MDS) Reference : Advanced Introduction to Machine Learning, CMU-10715

Outline • Introduction • Principal Component Analysis (PCA) • Linear Discriminant Analysis (LDA) • Multi-Dimensional Scaling (MDS) • Isometric Feature Mapping (Isomap) • Locally Linear Embedding (LLE) • Local Discriminant Embedding (LDE) • Maximum Variance Unfolding (MVU) • Laplacian Eigenmap • Demo • summary
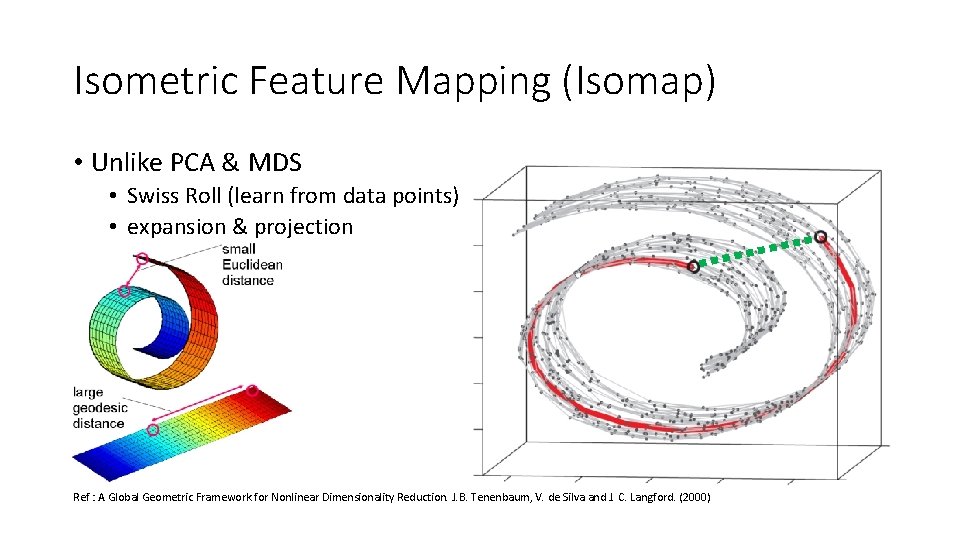
Isometric Feature Mapping (Isomap) • Unlike PCA & MDS • Swiss Roll (learn from data points) • expansion & projection Ref : A Global Geometric Framework for Nonlinear Dimensionality Reduction. J. B. Tenenbaum, V. de Silva and J. C. Langford. (2000)
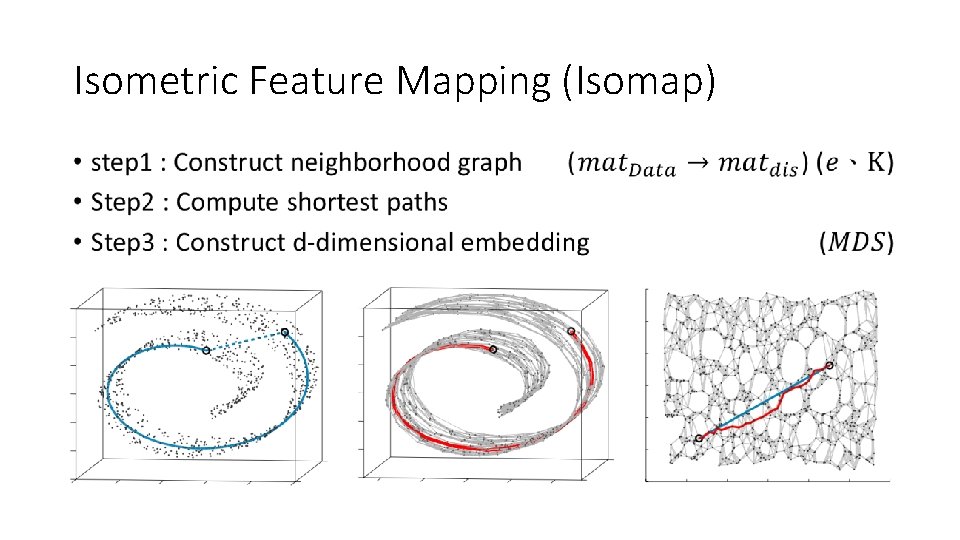
Isometric Feature Mapping (Isomap) •
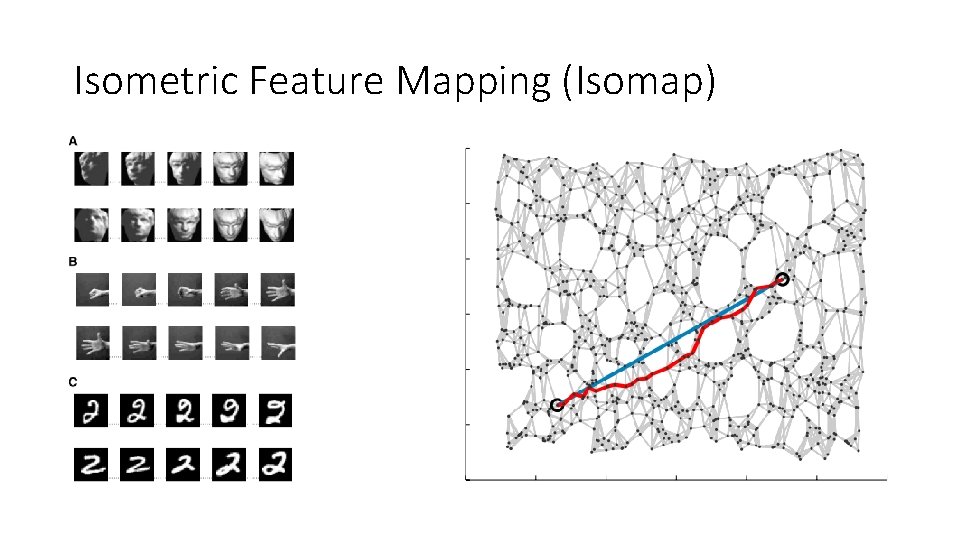
Isometric Feature Mapping (Isomap)
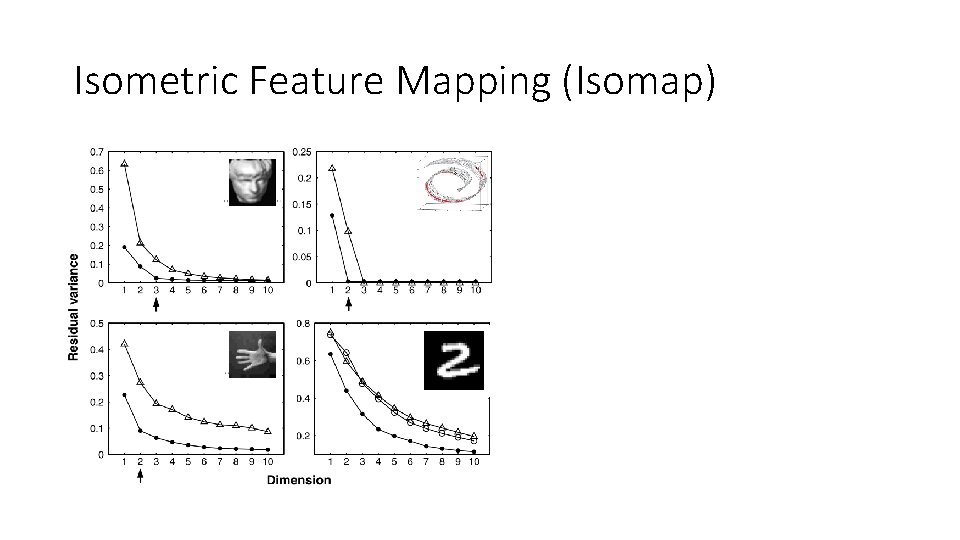
Isometric Feature Mapping (Isomap)

Outline • Introduction • Principal Component Analysis (PCA) • Linear Discriminant Analysis (LDA) • Multi-Dimensional Scaling (MDS) • Isometric Feature Mapping (Isomap) • Locally Linear Embedding (LLE) • Local Discriminant Embedding (LDE) • Maximum Variance Unfolding (MVU) • Laplacian Eigenmap • Demo • summary

Locally Linear Embedding (LLE) • Assumption : manifold is approximately “linear” when viewed locally Ref : Nonlinear Dimensionality Reduction by Locally Linear embedding. S. Roweis and L. Saul. (2000)
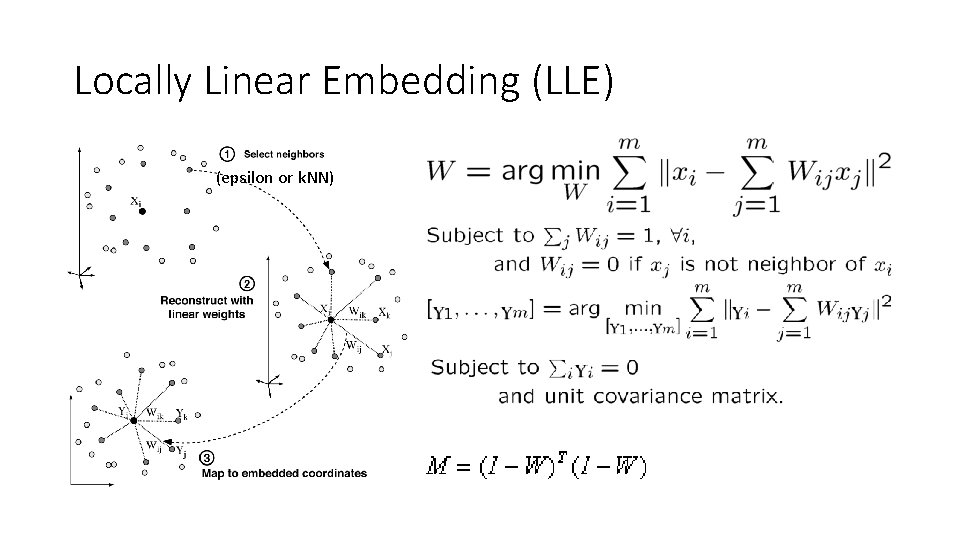
Locally Linear Embedding (LLE) (epsilon or k. NN)
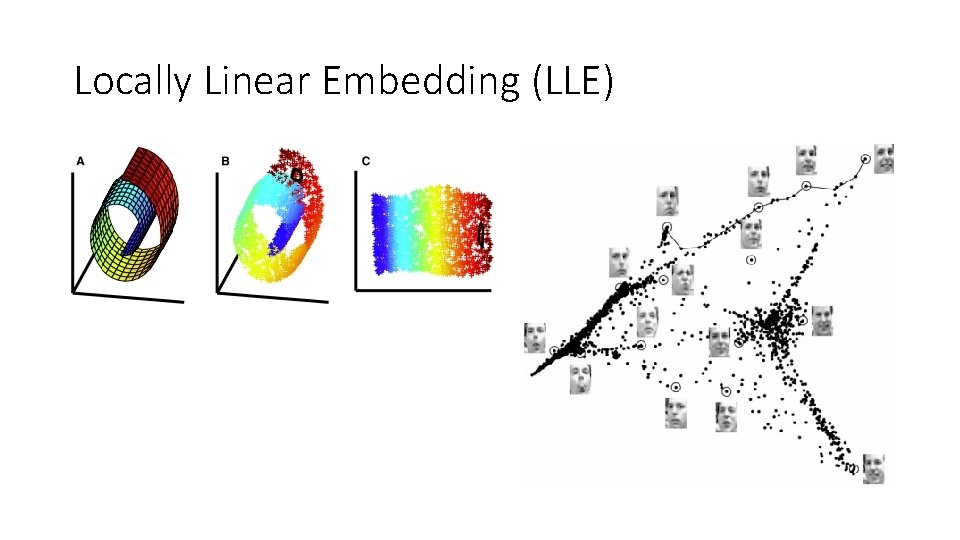
Locally Linear Embedding (LLE)

Outline • Introduction • Principal Component Analysis (PCA) • Linear Discriminant Analysis (LDA) • Multi-Dimensional Scaling (MDS) • Isometric Feature Mapping (Isomap) • Locally Linear Embedding (LLE) • Local Discriminant Embedding (LDE) • Maximum Variance Unfolding (MVU) • Laplacian Eigenmap • Demo • summary

Local Discriminant Embedding (LDE) • Isomap & LLE • limit : • representation training (≠classification) • → Local Discriminant Embedding (LDE) • Like LDA Ref : Local discriminant embedding and its variants. CVPR 2005. IEEE
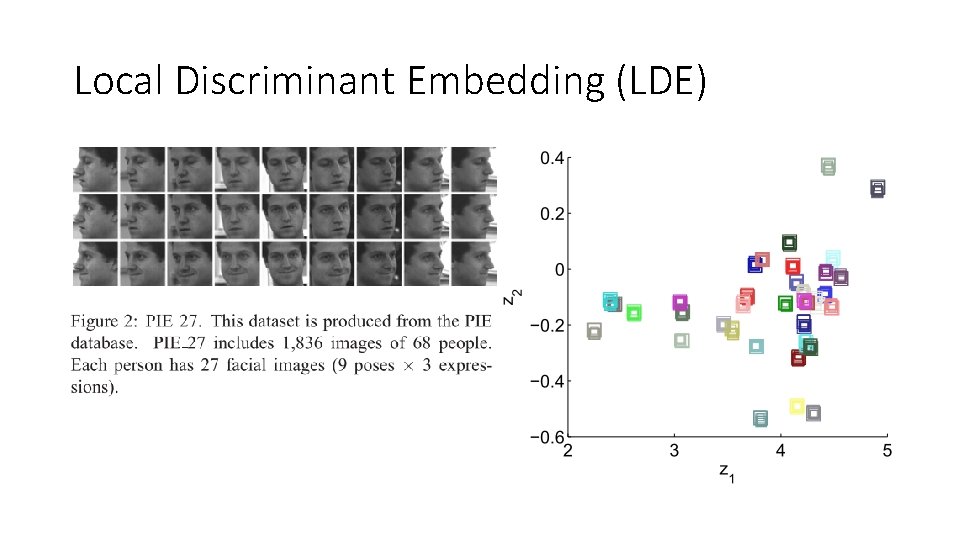
Local Discriminant Embedding (LDE)

Outline • Introduction • Principal Component Analysis (PCA) • Linear Discriminant Analysis (LDA) • Multi-Dimensional Scaling (MDS) • Isometric Feature Mapping (Isomap) • Locally Linear Embedding (LLE) • Local Discriminant Embedding (LDE) • Maximum Variance Unfolding (MVU) • Laplacian Eigenmap • Demo • summary

Maximum Variance Unfolding (MVU) • Ref : Unsupervised learning of image manifolds by semidefinite programming (2004) IEEE

Maximum Variance Unfolding (MVU) Gram matrices Max

Maximum Variance Unfolding (MVU)

Maximum Variance Unfolding (MVU) Cholesky decomposition

Outline • Introduction • Principal Component Analysis (PCA) • Linear Discriminant Analysis (LDA) • Multi-Dimensional Scaling (MDS) • Isometric Feature Mapping (Isomap) • Locally Linear Embedding (LLE) • Local Discriminant Embedding (LDE) • Maximum Variance Unfolding (MVU) • Laplacian Eigenmap • Demo • summary

Laplacian Eigenmap • like LLE • use graph theory’s Laplacian matrix Ref : Laplacian eigenmaps for dimensionality reduction and data representation (2003)

Laplacian Eigenmap • goal : • 1. KNN • 2. weight • 3. Laplacian matrix

Laplacian Eigenmap

Outline • Introduction • Principal Component Analysis (PCA) • Linear Discriminant Analysis (LDA) • Multi-Dimensional Scaling (MDS) • Isometric Feature Mapping (Isomap) • Locally Linear Embedding (LLE) • Local Discriminant Embedding (LDE) • Maximum Variance Unfolding (MVU) • Laplacian Eigenmap • Demo • summary

Demo Ref : http: //www. math. ucla. edu/~wittman/mani Advanced Introduction to Machine Learning, CMU-10715
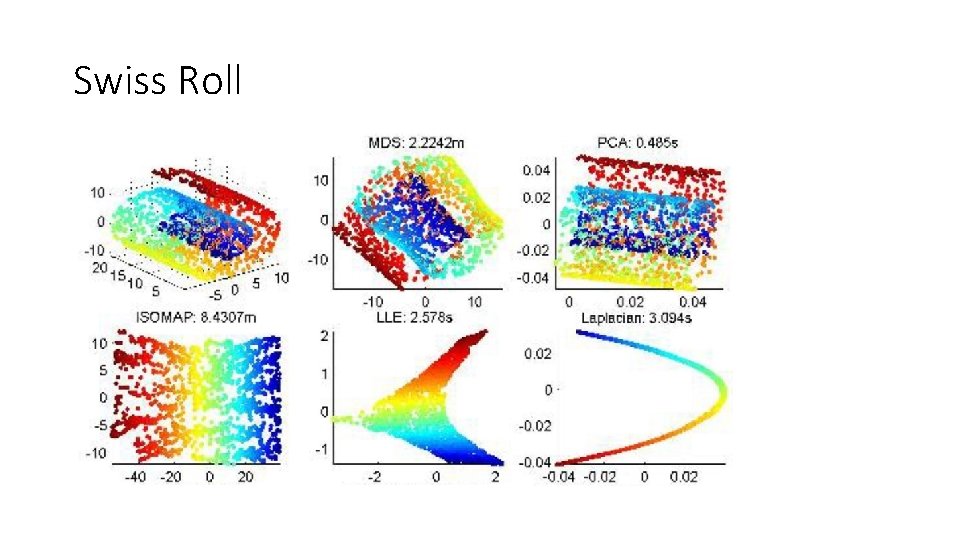
Swiss Roll
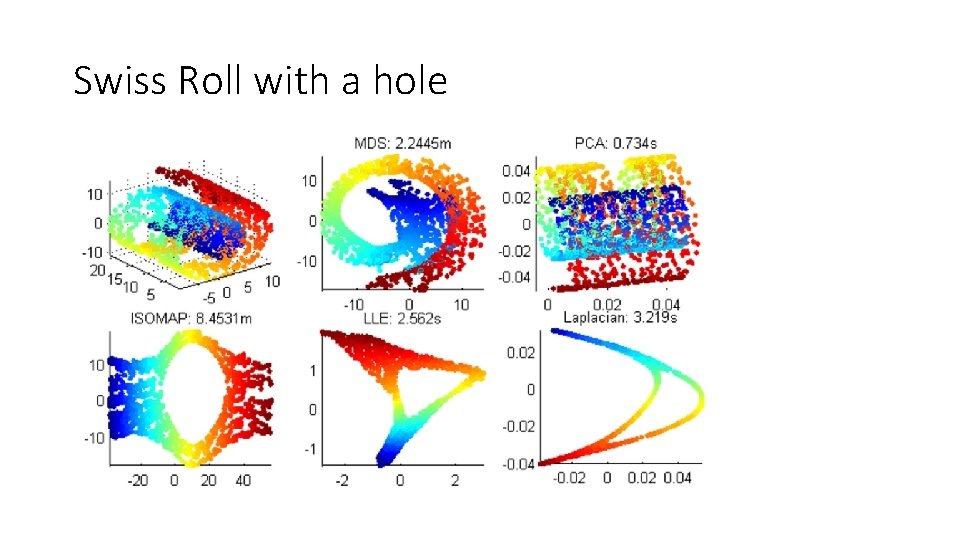
Swiss Roll with a hole
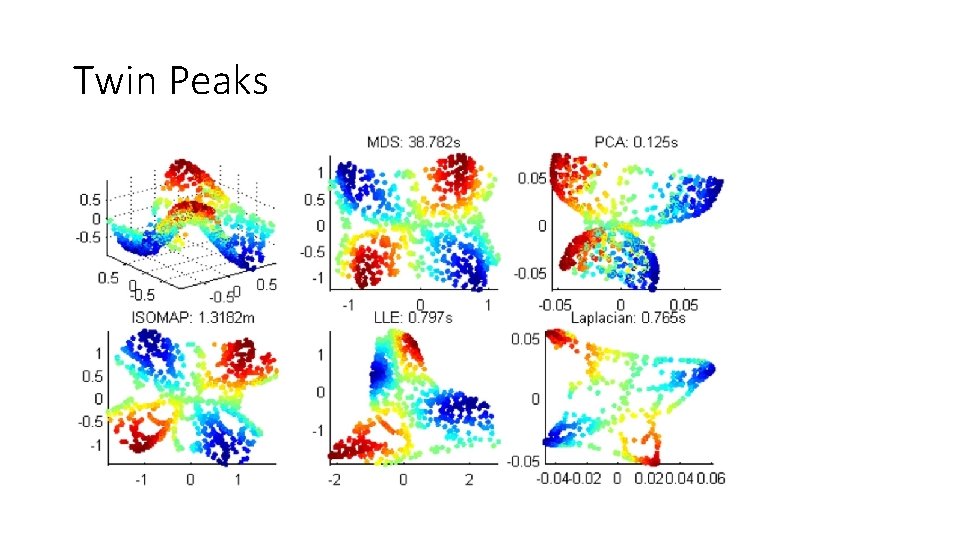
Twin Peaks
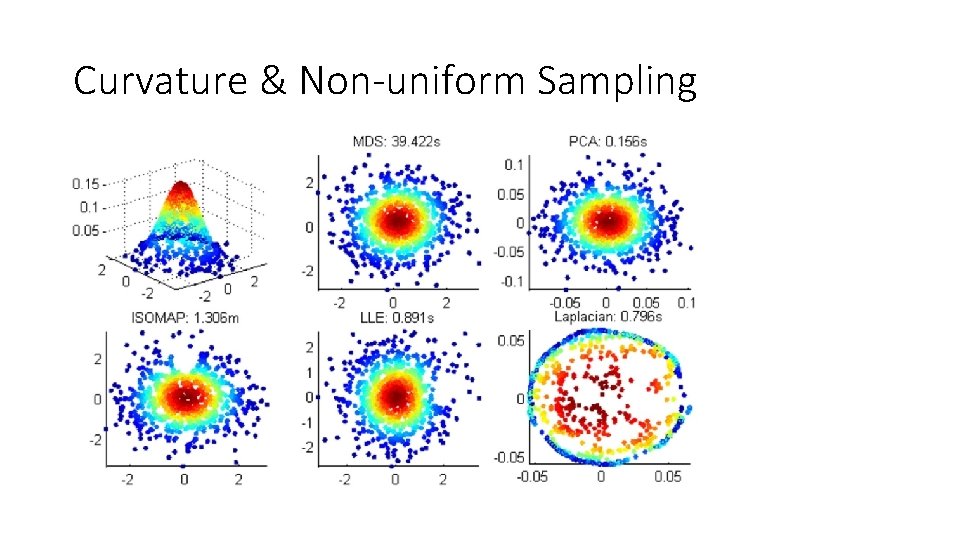
Curvature & Non-uniform Sampling
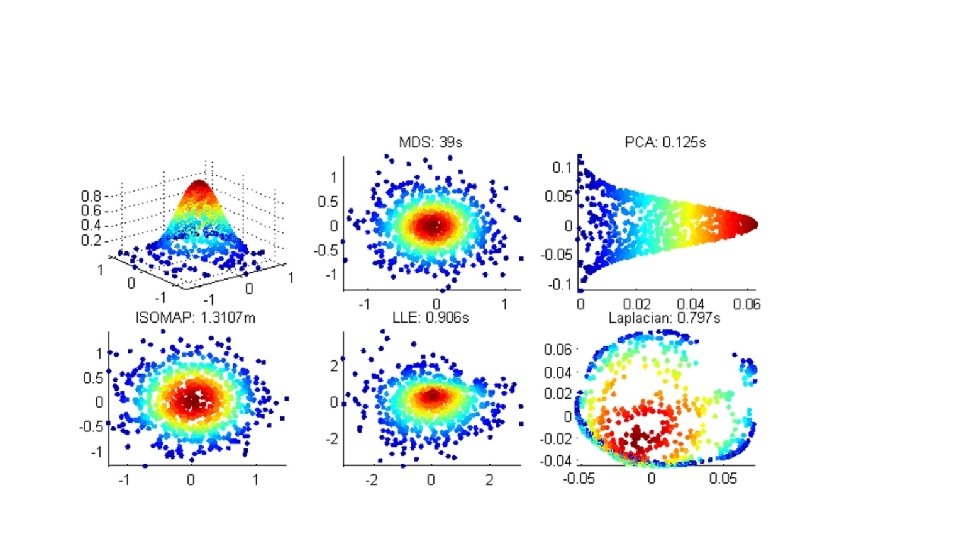
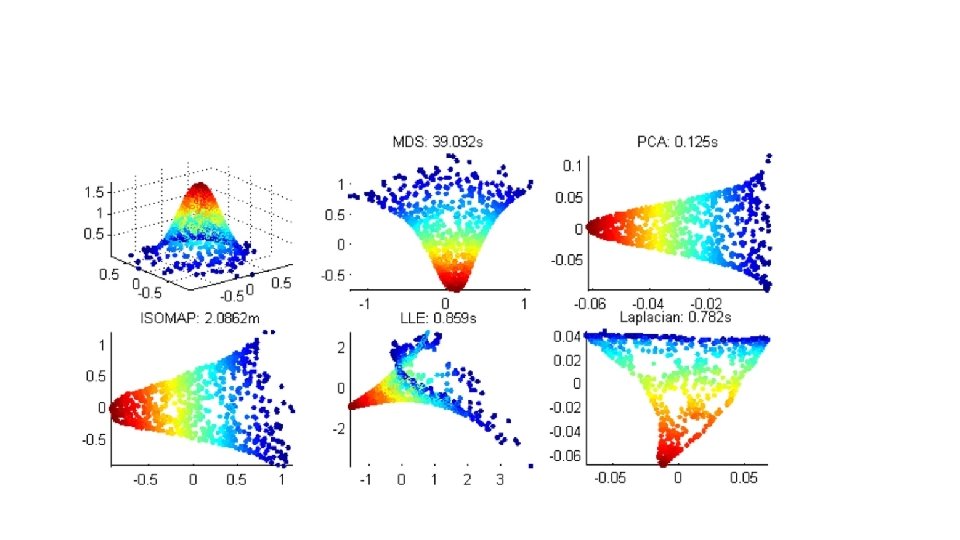
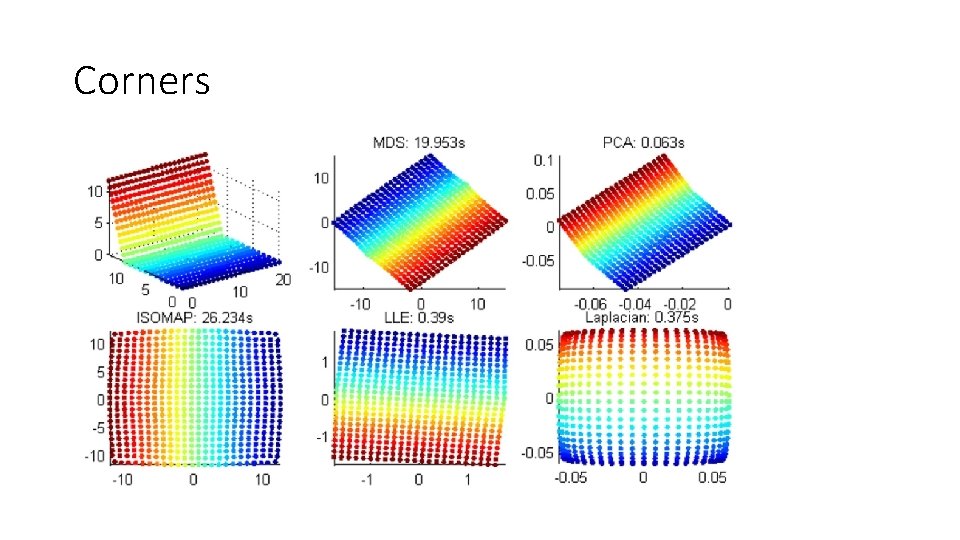
Corners
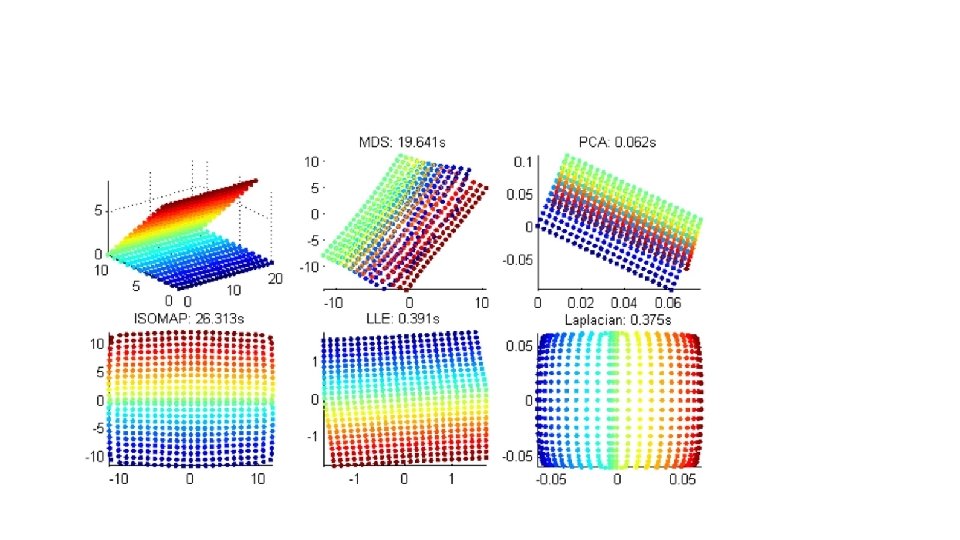
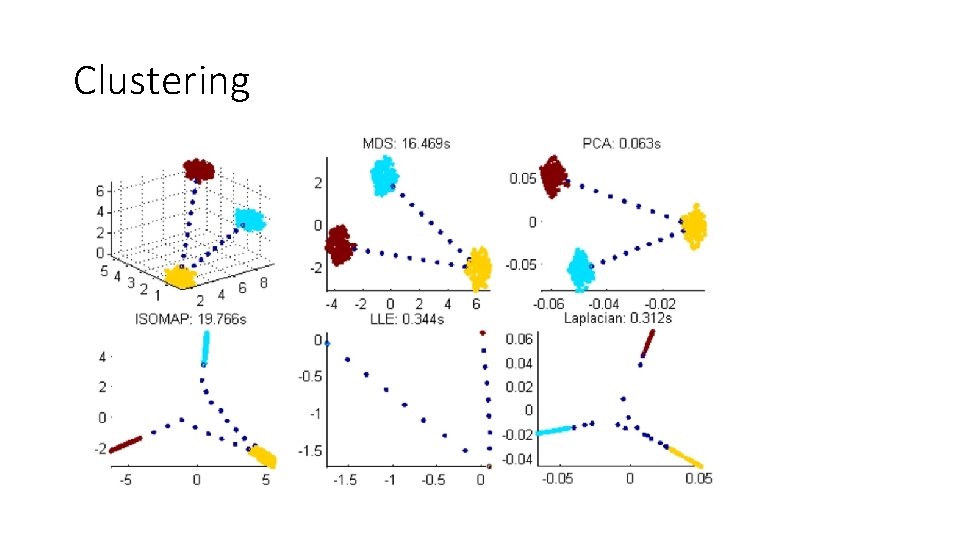
Clustering
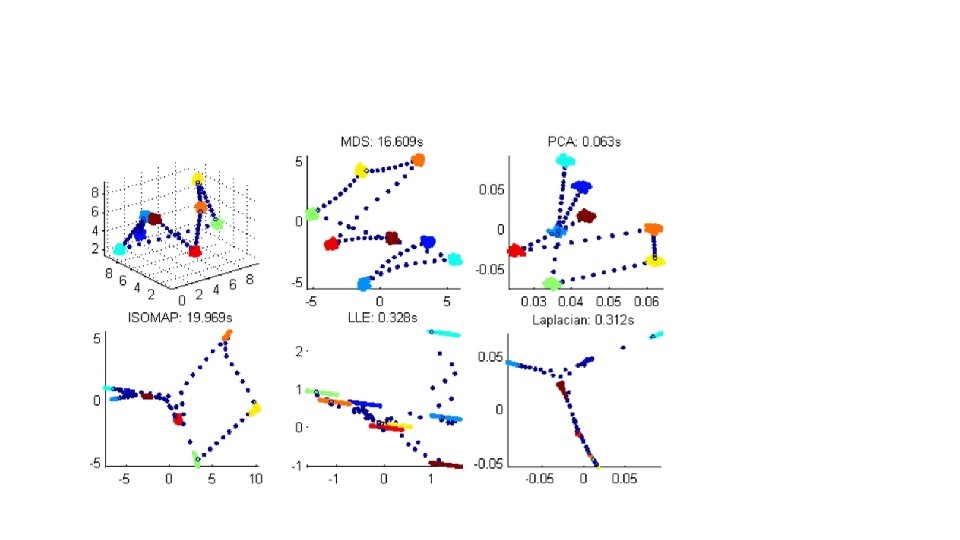
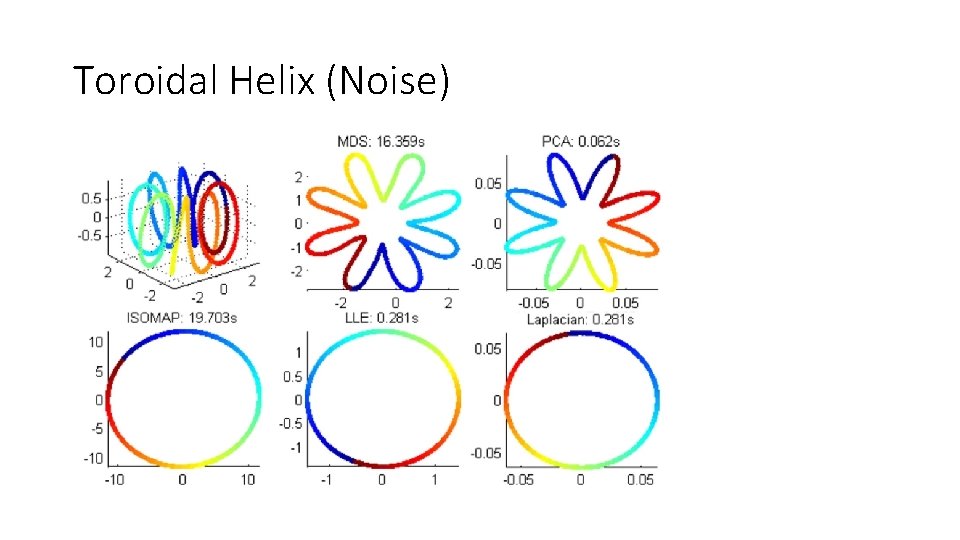
Toroidal Helix (Noise)
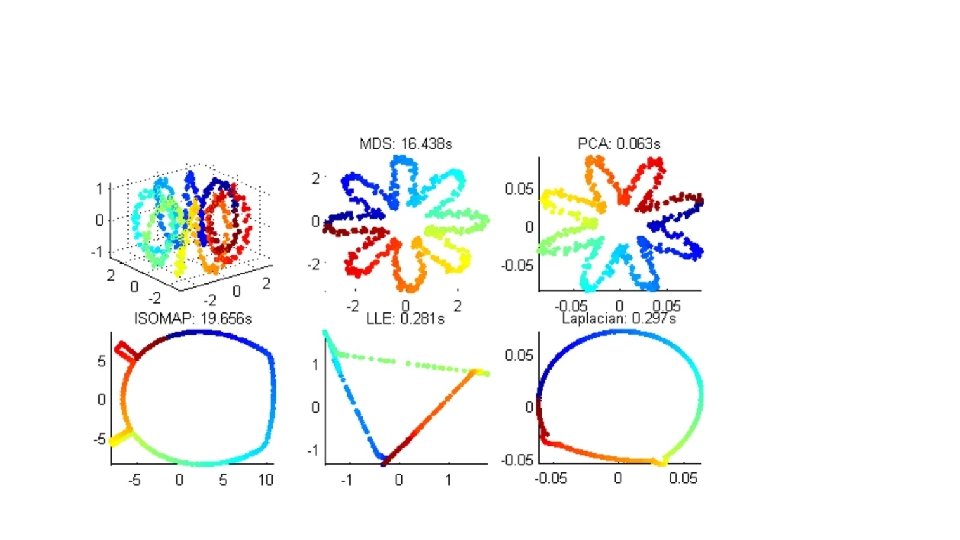
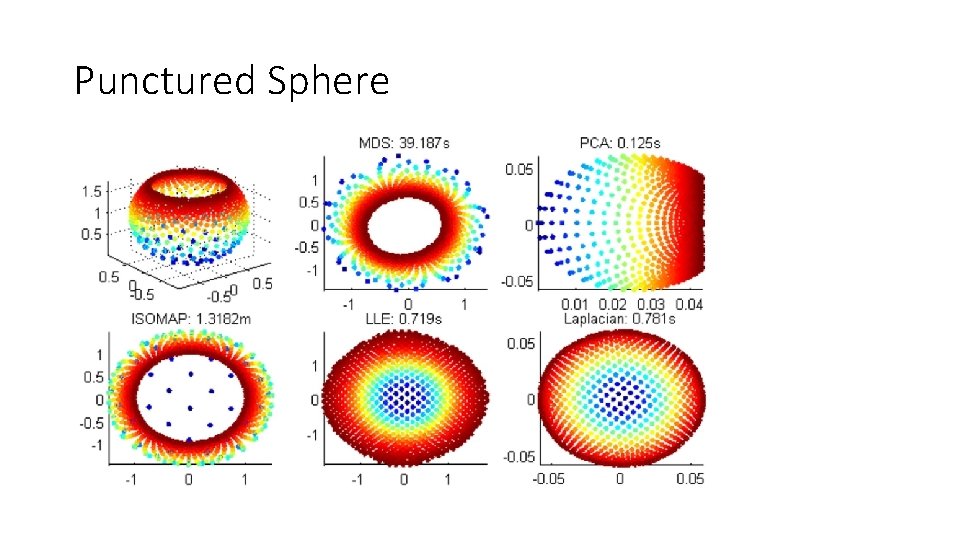
Punctured Sphere
High-Dimensional Data
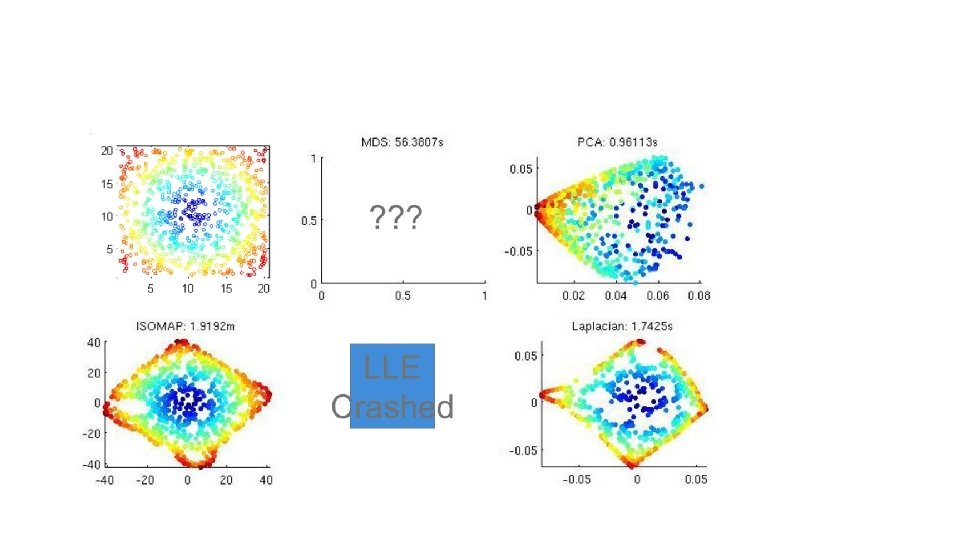

Outline • Introduction • Principal Component Analysis (PCA) • Linear Discriminant Analysis (LDA) • Multi-Dimensional Scaling (MDS) • Isometric Feature Mapping (Isomap) • Locally Linear Embedding (LLE) • Local Discriminant Embedding (LDE) • Maximum Variance Unfolding (MVU) • Laplacian Eigenmap • Demo • summary
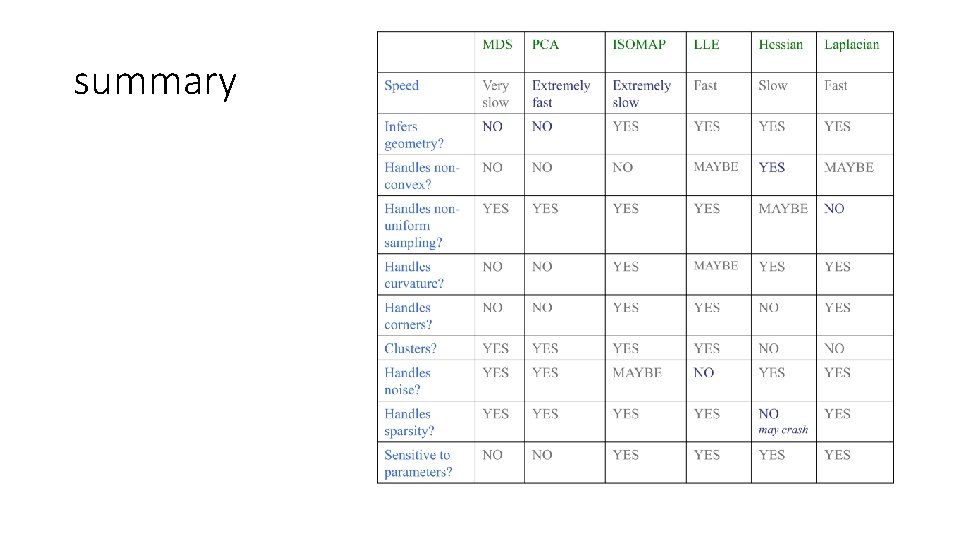
summary

Reference • Modern Multidimensional Scaling: theory and applications(2005) • The Manifold Ways of Perception. H. Seung and D. Lee. (2000) • A Global Geometric Framework for Nonlinear Dimensionality Reduction. J. B. Tenenbaum, V. de Silva and J. C. Langford. (2000) • Nonlinear Dimensionality Reduction by Locally Linear embedding. S. Roweis and L. Saul. (2000) • Local discriminant embedding and its variants. CVPR 2005. IEEE • Unsupervised learning of image manifolds by semidefinite programming (2004) IEEE • Laplacian eigenmaps for dimensionality reduction and data representation (2003) • 中央研究院週報 (第 1058期) 流行學習與人臉辨識 • http: //ocw. nthu. edu. tw/ocw/index. php? page=chapter&cid=53&chid=664 • http: //www. cnblogs. com/Left. Not. Easy/archive/2011/01/08/lda-and-pca-machine-learning. html • https: //ccjou. wordpress. com/2013/05/29/%E 5%8 F%A 4%E 5%85%B 8%E 5%A 4%9 A%E 7%B 6%AD%E 6%A 8%99%E 5%BA%A 6%E 6%B 3%95 -mds/ • Advanced Introduction to Machine Learning, CMU-10715 • http: //www. math. ucla. edu/~wittman/mani

- Slides: 64