Manifold learning and pattern matching with entropic graphs

Manifold learning and pattern matching with entropic graphs Alfred O. Hero Dept. EECS, Dept Biomed. Eng. , Dept. Statistics University of Michigan - Ann Arbor hero@eecs. umich. edu http: //www. eecs. umich. edu/~hero

Multimodality Face Matching

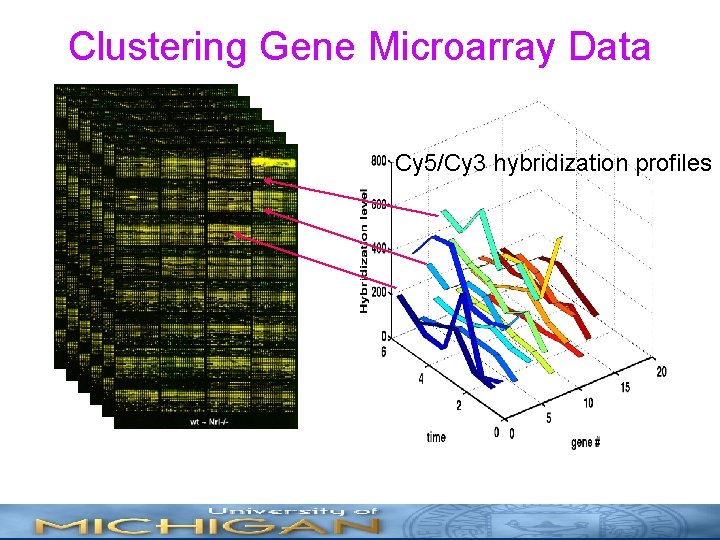
Clustering Gene Microarray Data Cy 5/Cy 3 hybridization profiles

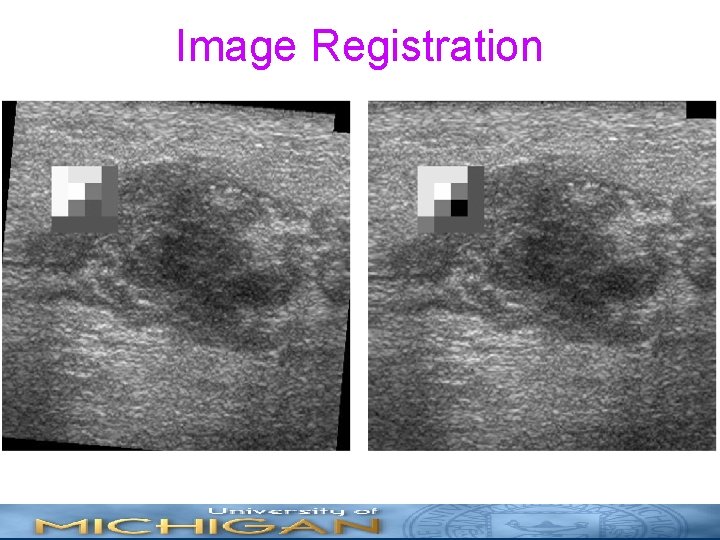
Image Registration

Vehicle Classification • 128 x 128 images of three vehicles over 1 deg increments of 360 deg azimuth at 0 deg elevation Truck T 62 HMMV Courtesy of Center for Imaging Science, JHU • The 3(360)=1080 images evolve on a lower dimensional imbedded manifold in R^(16384)

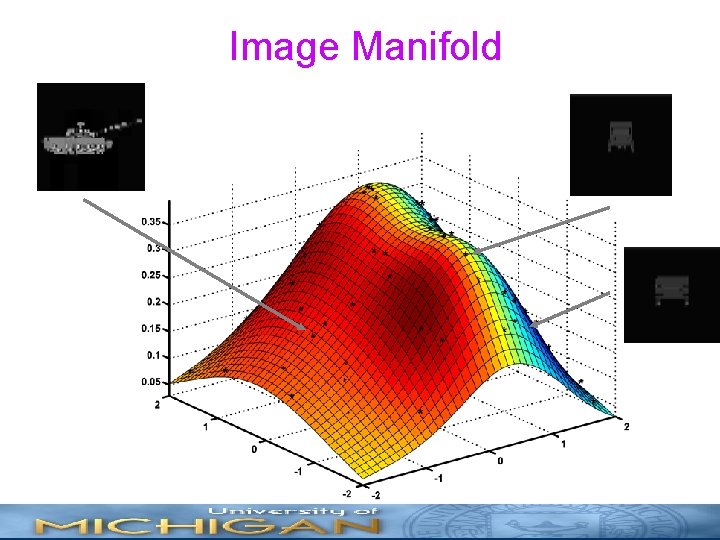
Image Manifold

What is manifold learning good for? • Interpreting high dimensional data • Discovery and exploitation of lower dimensional structure • Deducing non-linear dependencies between populations • Improving detection and classification performance • Improving image compression performance

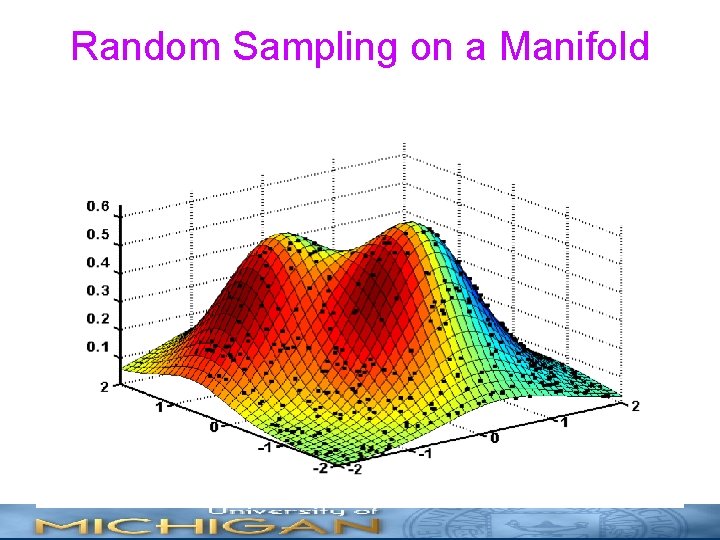
Random Sampling on a Manifold

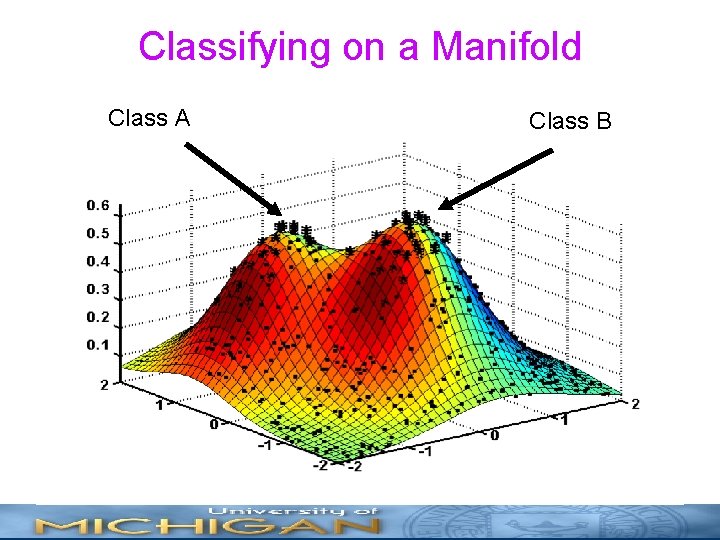
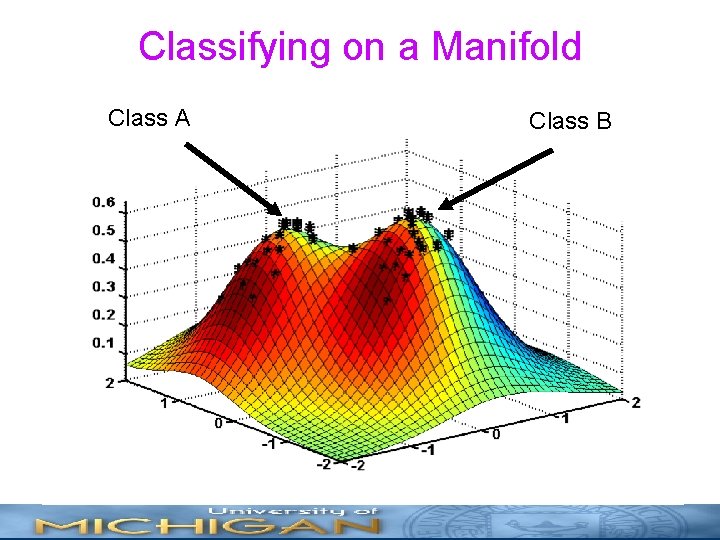
Classifying on a Manifold Class A Class B

Background on Manifold Learning • Manifold intrinsic dimension estimation – – Local KLE, Fukunaga, Olsen (1971) Nearest neighbor algorithm, Pettis, Bailey, Jain, Dubes (1971) Fractal measures, Camastra and Vinciarelli (2002) Packing numbers, Kegl (2002) • Manifold Reconstruction – – Isomap-MDS, Tenenbaum, de Silva, Langford (2000) Locally Linear Embeddings (LLE), Roweiss, Saul (2000) Laplacian eigenmaps (LE), Belkin, Niyogi (2002) Hessian eigenmaps (HE), Grimes, Donoho (2003) • Characterization of sampling distributions on manifolds – Statistics of directional data, Watson (1956), Mardia (1972) – Statistics of shape, Kendall (1984), Kent, Mardia (2001) – Data compression on 3 D surfaces, Kolarov, Lynch (1997)

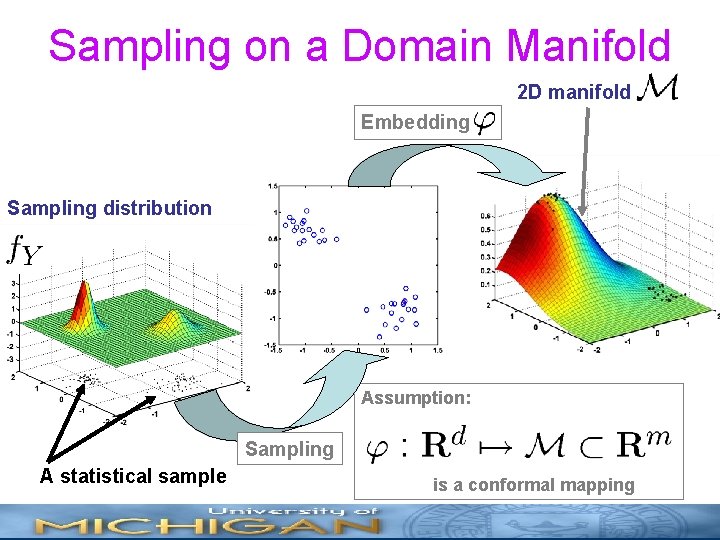
Sampling on a Domain Manifold 2 D manifold Embedding Sampling distribution Assumption: Sampling A statistical sample is a conformal mapping

Alpha-Entropy and Divergence • Alpha-entropy • Alpha-divergence • Other alpha-dissimilarity measures – Alpha-Jensen difference – Alpha geometric-arithmetic (GA) divergence

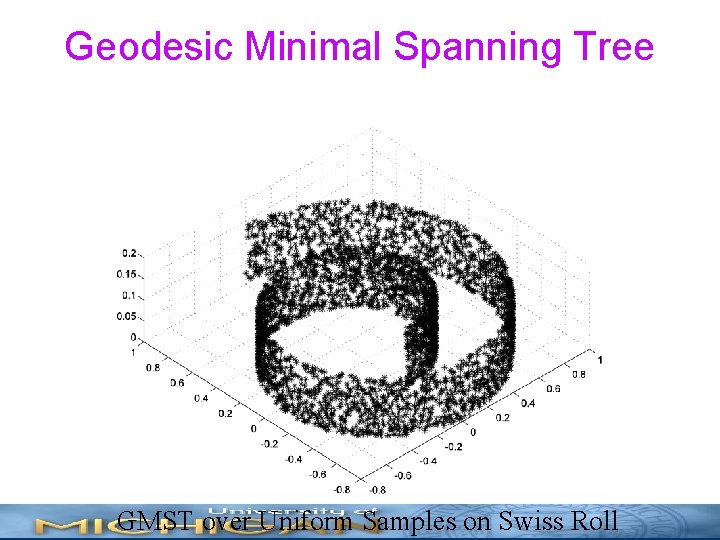
MST and Geodesic MST • For a set of points in ddimensional Euclidean space, the Euclidean MST with edge power weighting gamma is defined as • edge lengths of a spanning tree over • pairwise distance matrix of complete graph • When the matrix is constructed from geodesic distances between points on , e. g. using ISOMAP, we obtain the Geodesic MST

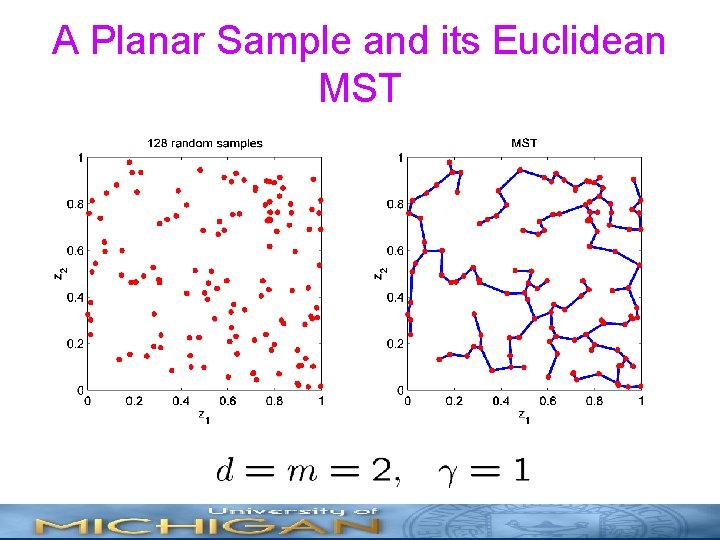
A Planar Sample and its Euclidean MST

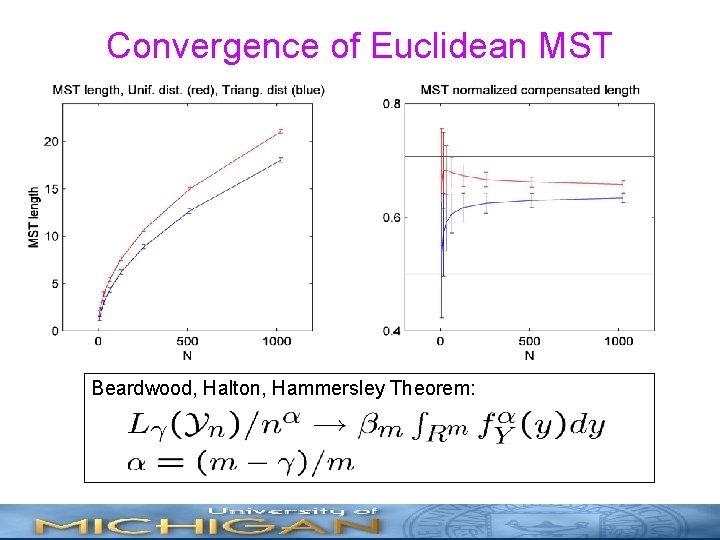
Convergence of Euclidean MST Beardwood, Halton, Hammersley Theorem:

Key Result for GMST Ref: Costa&Hero: TSP 2003

Special Cases • Isometric embedding (ISOMAP) • Conformal embedding (C-ISOMAP)

Remarks • Result holds for many other combinatorial optimization algorithms (Costa&Hero: 2003) – – K-NNG Steiner trees Minimal matchings Traveling Salesman Tours • a. s. convergence rates (Hero&etal: 2002) • For isometric embeddings Jacobian does not have to be estimated for dimension estimation

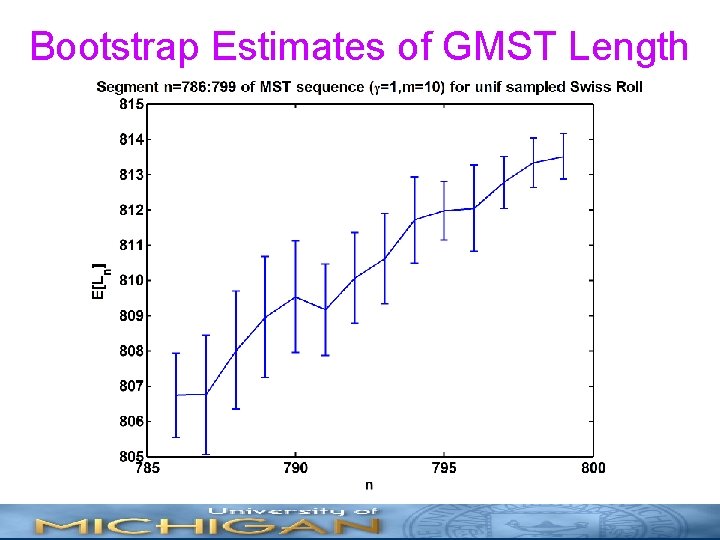
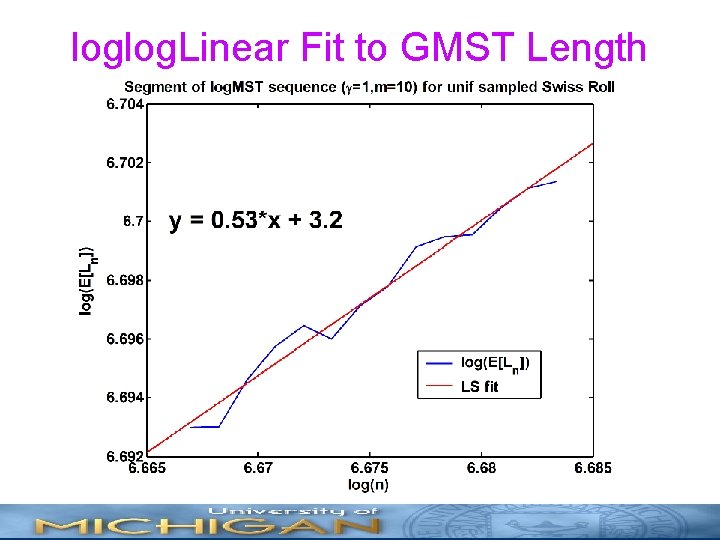
Joint Estimation Algorithm • Assume large-n log-affine model • Use bootstrap resampling to estimate mean MST length and apply LS to jointly estimate slope and intercept from sequence • Extract d and H from slope and intercept

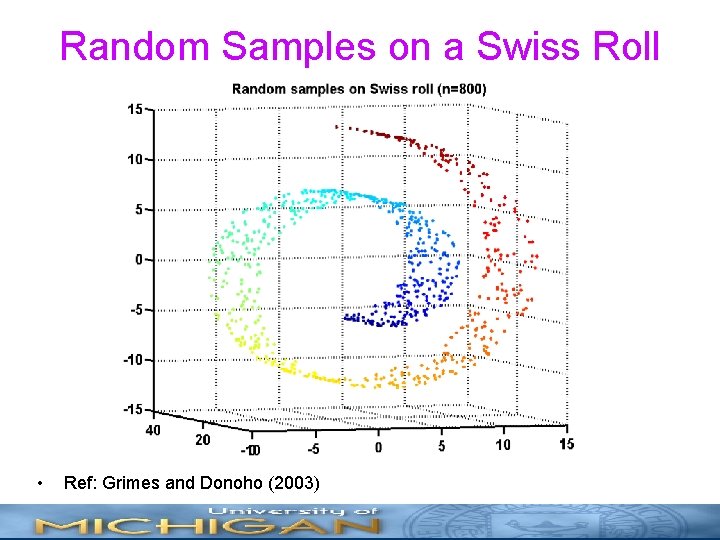
Random Samples on a Swiss Roll • Ref: Grimes and Donoho (2003)

Bootstrap Estimates of GMST Length

loglog. Linear Fit to GMST Length

Dimension and Entropy Estimates • From LS fit find: • Intrinsic dimension estimate • Alpha-entropy estimate (nats)

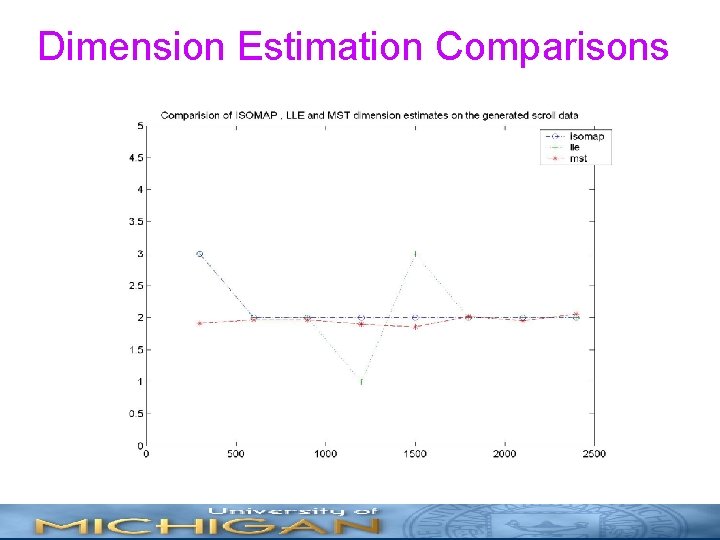
Dimension Estimation Comparisons

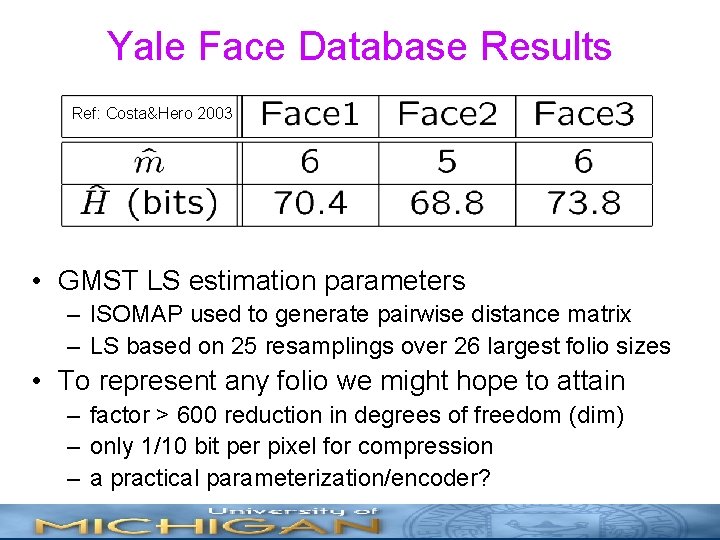
Practical Application • Yale face database 2 – Photographic folios of many people’s faces – Each face folio contains images at 585 different illumination/pose conditions – Subsampled to 64 by 64 pixels (4096 extrinsic dimensions) • Objective: determine intrinsic dimension and entropy of a face folio

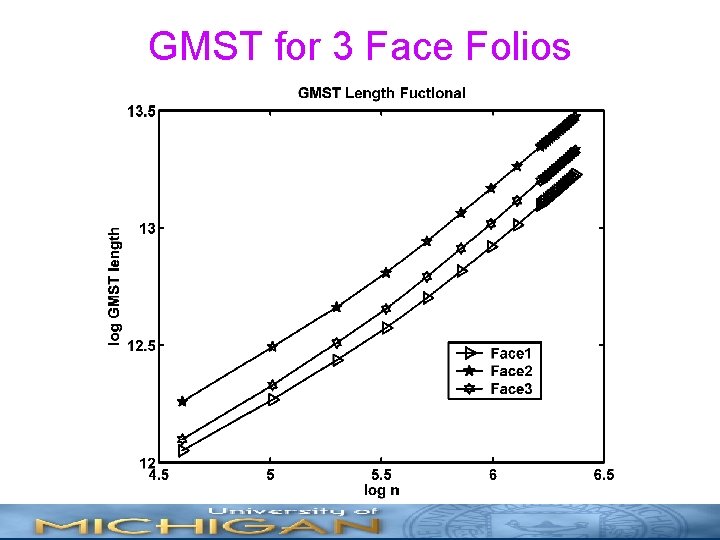
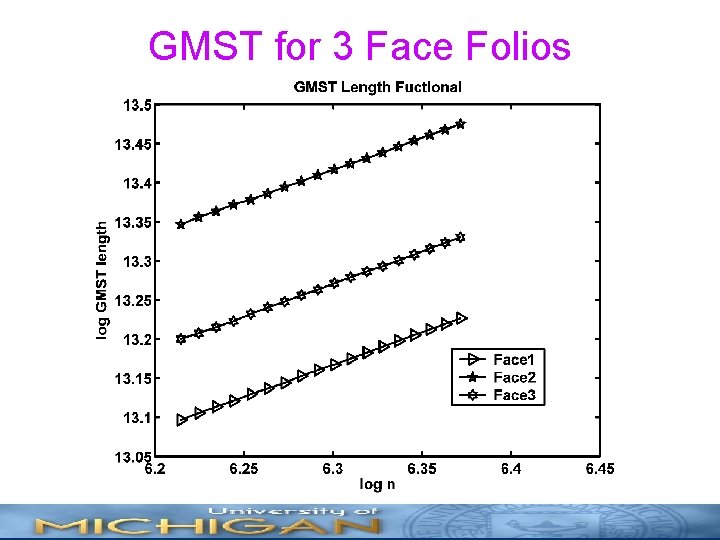
GMST for 3 Face Folios

GMST for 3 Face Folios

Yale Face Database Results Ref: Costa&Hero 2003 • GMST LS estimation parameters – ISOMAP used to generate pairwise distance matrix – LS based on 25 resamplings over 26 largest folio sizes • To represent any folio we might hope to attain – factor > 600 reduction in degrees of freedom (dim) – only 1/10 bit per pixel for compression – a practical parameterization/encoder?

Conclusions Advantages of Geodesic Entropic Graph Methods • Characterizing high dimension sampling distributions – Standard techniques (histogram, density estimation) fail due to curse of dimensionality – Entropic graphs can be used to construct consistent estimators of entropy and information divergence – Robustification to outliers via pruning • Manifold learning and model reduction – Standard techniques (LLE, MDS, LE, HE) rely on local linear fits – Entropic graph methods fit the manifold globally – Computational complexity is only n log n

Summary of Algorithm • Run ISOMAP or C-ISOMAP algorithm to generate pairwise distance matrix on intrinsic domain of manifold • Build geodesic entropic graph from pairwise distance matrix – MST: consistent estimator of manifold dimension and process alpha-entropy – K-NNG: consistent estimator of information divergence between labeled vectors • Use bootstrap resampling and LS fitting to extract rate of convergence (intrinsic dimension) and convergence factor (entropy) of entropic graph

Swiss Roll Example Uniform Samples on 3 D Imbedding of Swiss Roll

Geodesic Minimal Spanning Tree GMST over Uniform Samples on Swiss Roll

Geodesic MST on Imbedded Mixture GMST on Gaussian Samples on Swiss Roll

Classifying on a Manifold Class A Class B