Manajemen Proyek Project Management 3 Perencanaan Proyek Probabilistic

Manajemen Proyek Project Management

3. Perencanaan Proyek Probabilistic Time Estimates Suatu aktivitas bisa saja dapat dilakukan sesuai dengan skedul yang pasti tapi bisa juga mengalami berbagai hambatan atau gangguan yang akan mengkibatkan variasi atau perubahan waktu yang direncanakan. Jadi dalam keadaan ini bisa terjadi ketidak pastian. Untuk meniminmisasi kondisi seperti ini dalam network planning biasa digunakkan pendekatan prbabilistic atau probabilistic approach. Probabilistic approach yang dianut dapat meliputi 3 waktu estimasi (three times estimates) yaitu : 1. Optimistic time : Lama waktu yang dibutuhkan dalam kondisi optimum untuk penyelesaian pekerjaan, ditulis dengan to. 2. Pessimistic time : Lama waktu yang dibutuhkan dalam kondisi terburuk untuk penyelesaian pekerjaan, diberi notasi tp. 3. Most likely time : Lama waktu yang dibutuhkan dalam kondisi sesuai yang diharapkan, diberi notasi tm Untuk menghitung tiga kenmungkinan tersebut digunakan distribusi Beta Project Management

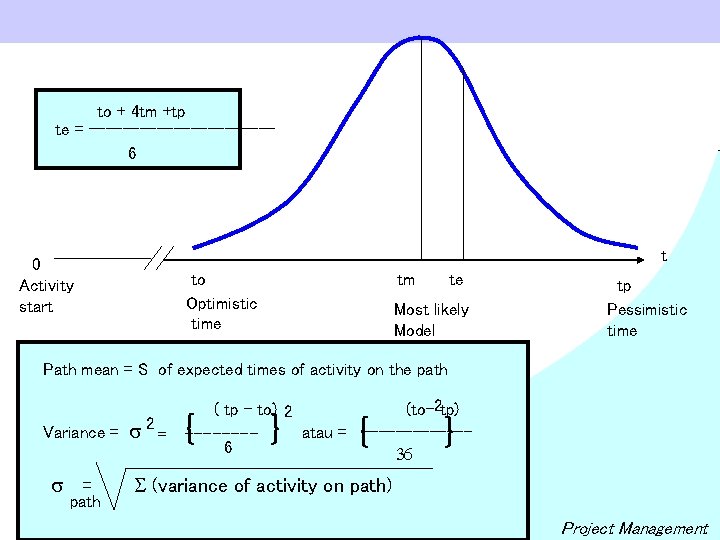
to + 4 tm +tp te = -----------6 t 0 Activity start to Optimistic time tm te Most likely Model tp Pessimistic time Path mean = S of expected times of activity on the path Variance = s s = path 2 = ( tp – to) 2 (to-2 tp) -------atau = ------6 36 { } S (variance of activity on path) Project Management

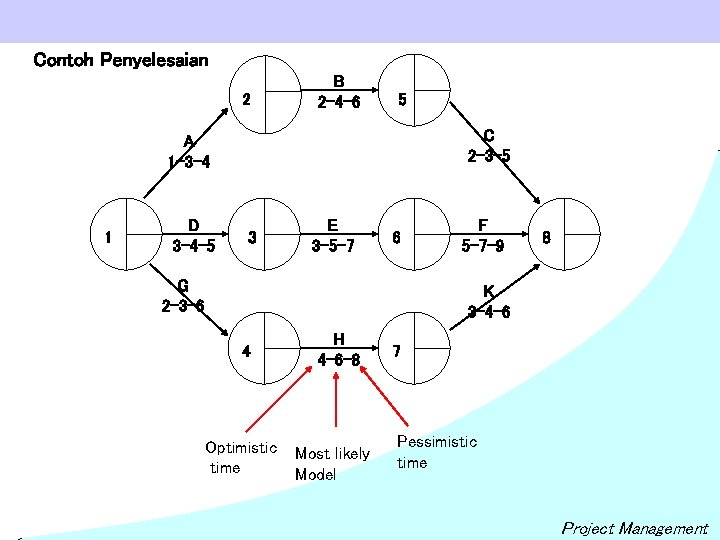
Contoh Penyelesaian 2 B 2 -4 -6 5 C 2 -3 -5 A 1 -3 -4 1 D 3 -4 -5 3 E 3 -5 -7 6 G 2 -3 -6 F 5 -7 -9 8 K 3 -4 -6 4 Optimistic time H 4 -6 -8 Most likely Model 7 Pessimistic time Project Management

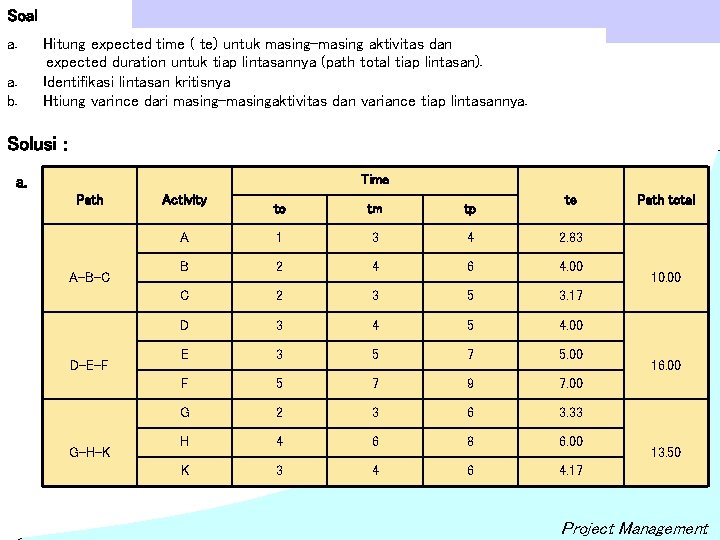
Soal a. a. b. Hitung expected time ( te) untuk masing-masing aktivitas dan expected duration untuk tiap lintasannya (path total tiap lintasan). Identifikasi lintasan kritisnya Htiung varince dari masing-masingaktivitas dan variance tiap lintasannya. Solusi : Time a. Path A-B-C D-E-F G-H-K Activity te to tm tp A 1 3 4 2. 83 B 2 4 6 4. 00 C 2 3 5 3. 17 D 3 4 5 4. 00 E 3 5 7 5. 00 F 5 7 9 7. 00 G 2 3 6 3. 33 H 4 6 8 6. 00 K 3 4 6 4. 17 Path total 10. 00 16. 00 13. 50 Project Management

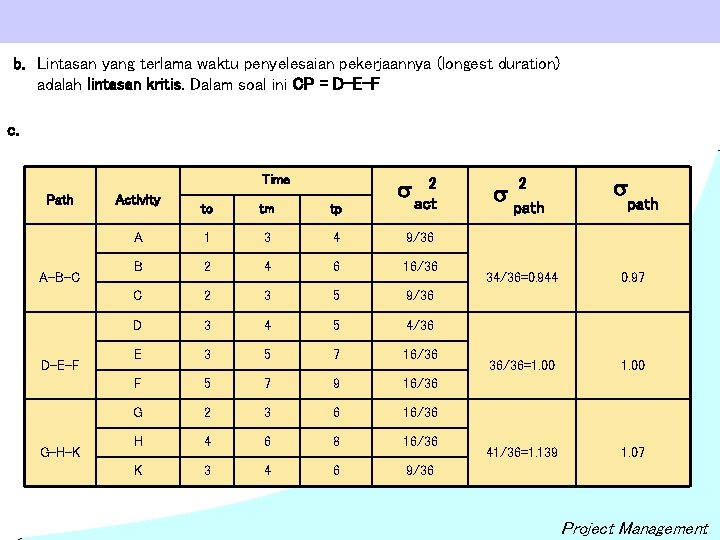
b. Lintasan yang terlama waktu penyelesaian pekerjaannya (longest duration) adalah lintasan kritis. Dalam soal ini CP = D-E-F c. Time Path A-B-C D-E-F G-H-K to tm tp s act 2 A 1 3 4 9/36 B 2 4 6 16/36 C 2 3 5 9/36 D 3 4 5 4/36 E 3 5 7 16/36 F 5 7 9 16/36 G 2 3 6 16/36 H 4 6 8 16/36 K 3 4 6 9/36 Activity 2 s path 34/36=0. 944 0. 97 36/36=1. 00 41/36=1. 139 1. 07 Project Management

The summing of activity time result in normal distribution path activity = + + beta activity beta normal Menentukan probabilitas lintasan Probabilitas bahwa lintasan yang diberikanakan selesai pada lama waktu yang spesifik Dapat dihitung dengan menggunakan rumus sebagai berikut : Specified time - path mean Z = --------------------Path Standard deviation Project Management

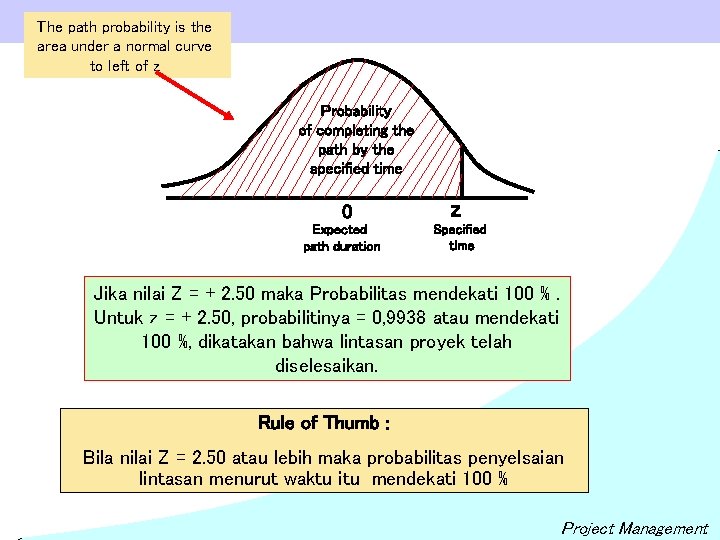
The path probability is the area under a normal curve to left of z Probability of completing the path by the specified time 0 Expected path duration z Specified time Jika nilai Z = + 2. 50 maka Probabilitas mendekati 100 %. Untuk z = + 2. 50, probabilitinya = 0, 9938 atau mendekati 100 %, dikatakan bahwa lintasan proyek telah diselesaikan. Rule of Thumb : Bila nilai Z = 2. 50 atau lebih maka probabilitas penyelsaian lintasan menurut waktu itu mendekati 100 % Project Management

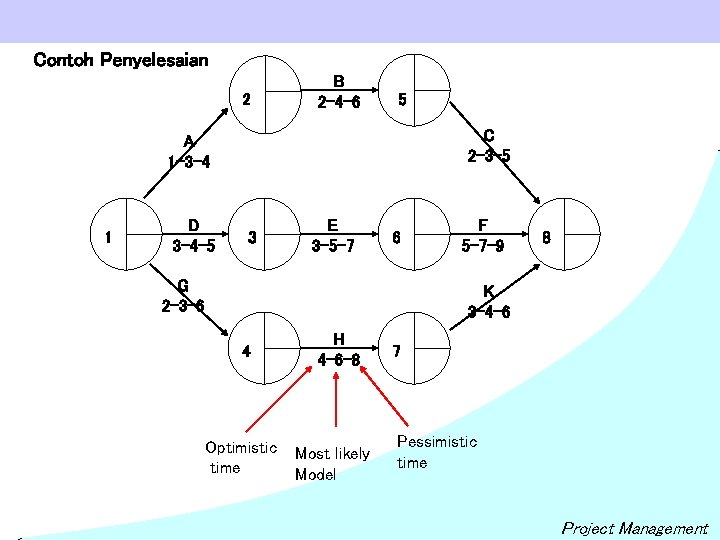
Contoh Penyelesaian 2 B 2 -4 -6 5 C 2 -3 -5 A 1 -3 -4 1 D 3 -4 -5 3 E 3 -5 -7 6 G 2 -3 -6 F 5 -7 -9 8 K 3 -4 -6 4 Optimistic time H 4 -6 -8 Most likely Model 7 Pessimistic time Project Management

Soal Probabilistic. a. b. c. d. Berdasarkan data sebelumnya bisa dikatakan bahwa lintasan disebut independent karena dari data diatas lintasan yang menunjukkan selesai lebih dari satu lintasan ( no activity is on more than one path) Berapa probabiltas proyek bisa selesai dalam waktu 17 minggu dari sejak start? Berapa probabiltas proyek bisa selesai dalam waktu 15 minggu dari sejak start? Berapa probabiltas proyek tidak akan bisa selesai dalam waktu 15 minggu dari sejak start? Untuk menjawab b, c, d kita bisa gambarkan letak distribusi lintasan yang kemungkinan overlap dengan waktu spesifik tadi sebagai berikut : lintasan A-B-C dan G-H-I berada dikiri dari waktu maka keduanya akan selesai pada minggu 17. Sedangkan D-E-F overlap, maka harus dihitung sbb: 17 - 16 Z = ------ = + 1. 00 Dari tabel Z= 1. 00 maka Probability = 0. 8413 atau 84, 13 % Project Management

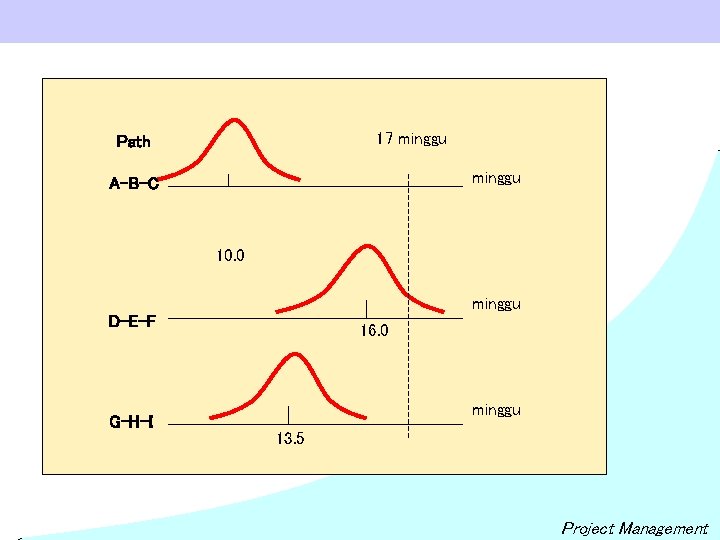
17 minggu Path minggu A-B-C 10. 0 minggu D-E-F G-H-I 16. 0 minggu 13. 5 Project Management

Rumus umum menghitung Kemungkinan selesai dalam waktu tertentu, adalah sebagai berikut : Buat lintasan yang dapat terjadi ( semua yang tercantum dalam network). 1. Hitung Expected path duration dan standard deviasi untuk tiap lintasan. 2. Hitung Z dengan rumus sbb : Z = Waktu yang ditentukan – Expected path duration -------------------------------- Standard deviasi lintasan dimaksud 4. Hasilnya lihat pada table Z, angka tadi menunujukan probabilitas yang dicari! P( 17 minggu) Path z P(selesai dalam waktu 17 mg) 17 - 10 A-B-C D-E-F ------- = + 7. 22 0. 97 17 - 16 ------ = + 1. 00 17 – 13. 5 G-H-K ------ = + 3. 27 1. 00 = 100 % 0. 8413 = 84. 13 % 1. 00 X 0. 8413 X 1. 00 = 0. 8413 1. 00 = 100 % 1. 07 P( Selesai dalam waktu 17 minggu) = P (path A-B-C) X P( path D-E-F) X P(path F-G-K) Project Management

Path z P(selesai dalam waktu 15 mg) P( 15 minggu) = 15 - 10 A-B-C ------- = + 5. 15 0. 97 15 - 16 D-E-F ------ = - 1. 00 15 – 13. 5 G-H-I ------ = + 1. 40 1. 0000 = 100 % 0. 1587 = 15. 87 % 0. 9192 = 1. 00 X. 1587 x. 9192 =. 1459 91. 92 % 1. 07 Jadi : a. Probabilitas proyek selesai dalam waktu 15 minggu adalah = 0. 1459 b. Probabilitas proyek tidak selesai dalam waktu 15 minggu 1. 000 – 0. 1459 = 0. 8541 = Project Management

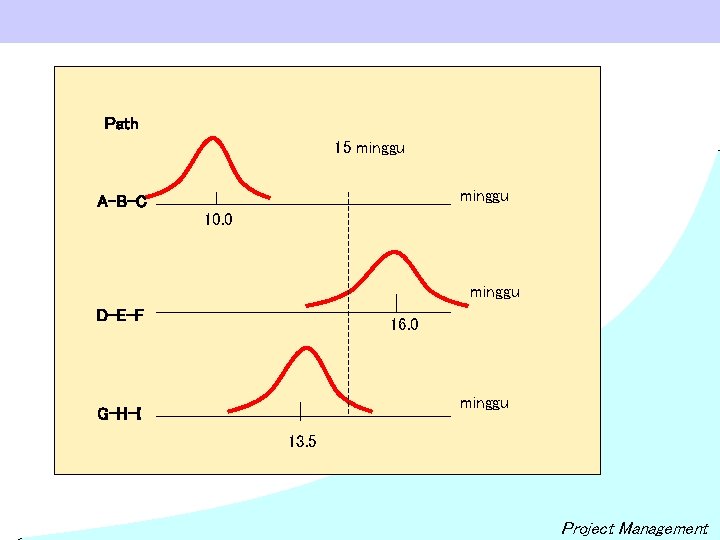
Path 15 minggu A-B-C 10. 0 minggu D-E-F 16. 0 minggu G-H-I 13. 5 Project Management

Time Cost Trade – Off = Crashing. Estimasi waktu kegiatan suatu proyek biasanya diassumsikan dengan tingkat kesiapan sumber daya tertentu. Namun pada kenyataanya bisa saja terjadi perubahan atau mengurangi waktu tersebut karena kebutuhan dengan cara menambah sumber daya tadi. Mengurangi durasi waktu pelaksanaan aktivitas tadi dikenal dengan sebutan Crashing atau CRASH. Kita harus mengkaji aktivitas mana saja yang diperlukan untuk dilaksanakan secara crasching. Yang harus dipunyai oleh seorang Manager proyek bila terjadi Crashing adalah : 1. Regular time dan Crash time untuk tiap aktivitas. 2. Regular cost dan estimasi crash cost untuk tiap aktivitas. 3. Daftar aktivitas yang berada pada lintasan ktiris. Untuk itu bila akan melakukan crash perhatikan hal-hal berikut : 1. Buat estimasi regular dan crash serta costnya bagi tiap aktivitas 2. Tentukan durasi setiap lintasan dan slack Tme dari lintasan tersebut. 3. Tentukan waktu kritidnya. 4. Crash bagi aktivitas kritis, walaupun cost bertambah namun tidak mengurangi benefit proyek secara keseluruhan. Project Management

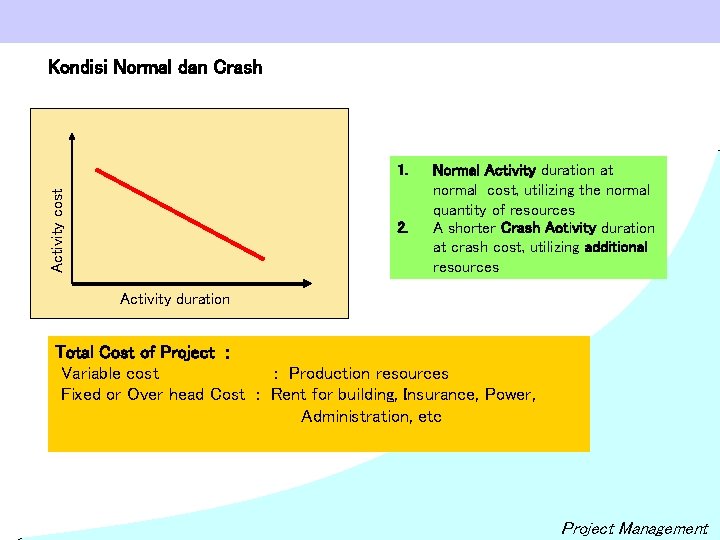
Kondisi Normal dan Crash Activity cost 1. 2. Normal Activity duration at normal cost, utilizing the normal quantity of resources A shorter Crash Activity duration at crash cost, utilizing additional resources Activity duration Total Cost of Project : Variable cost : Production resources Fixed or Over head Cost : Rent for building, Insurance, Power, Administration, etc Project Management

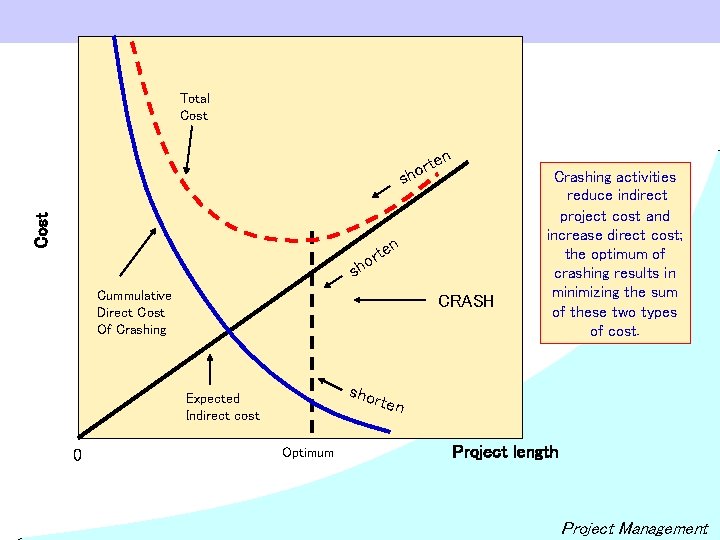
Total Cost n Cost s te r o h n s rte o h Cummulative Direct Cost Of Crashing CRASH shor Expected Indirect cost 0 Optimum Crashing activities reduce indirect project cost and increase direct cost; the optimum of crashing results in minimizing the sum of these two types of cost. ten Project length Project Management

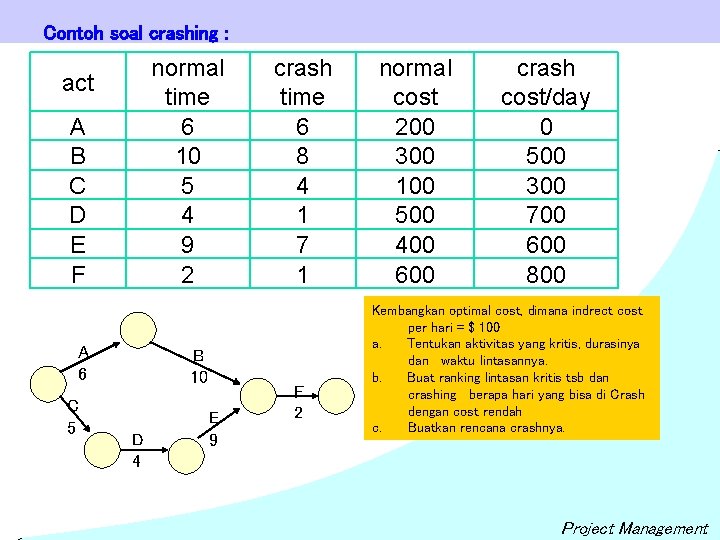
Contoh soal crashing : normal time 6 10 5 4 9 2 act A B C D E F A 6 C 5 B 10 D 4 E 9 crash time 6 8 4 1 7 1 F 2 normal cost 200 300 100 500 400 600 crash cost/day 0 500 300 700 600 800 Kembangkan optimal cost, dimana indrect cost per hari = $ 100 a. Tentukan aktivitas yang kritis, durasinya dan waktu lintasannya. b. Buat ranking lintasan kritis tsb dan crashing berapa hari yang bisa di Crash dengan cost rendah c. Buatkan rencana crashnya. Project Management

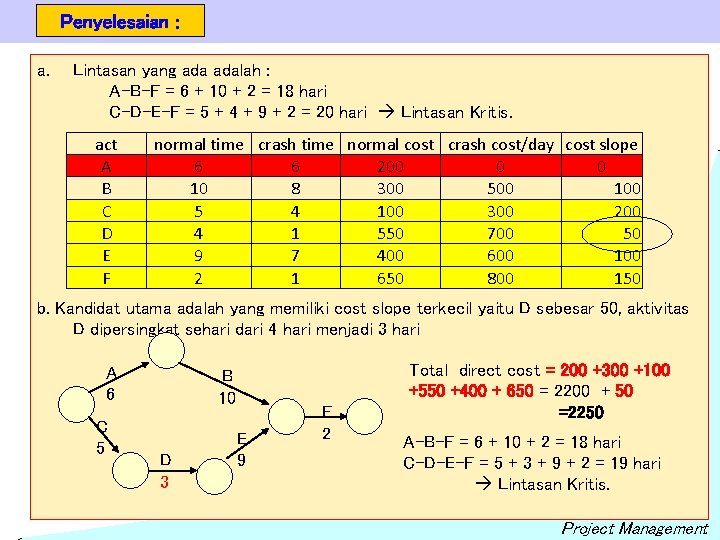
Penyelesaian : a. Lintasan yang adalah : A-B-F = 6 + 10 + 2 = 18 hari C-D-E-F = 5 + 4 + 9 + 2 = 20 hari Lintasan Kritis. act A B C D E F normal time crash time normal cost crash cost/day cost slope 6 6 200 0 0 10 8 300 500 100 5 4 100 300 200 4 1 550 700 50 9 7 400 600 100 2 1 650 800 150 b. Kandidat utama adalah yang memiliki cost slope terkecil yaitu D sebesar 50, aktivitas D dipersingkat sehari dari 4 hari menjadi 3 hari A 6 C 5 B 10 D 3 E 9 F 2 Total direct cost = 200 +300 +100 +550 +400 + 650 = 2200 + 50 =2250 A-B-F = 6 + 10 + 2 = 18 hari C-D-E-F = 5 + 3 + 9 + 2 = 19 hari Lintasan Kritis. Project Management

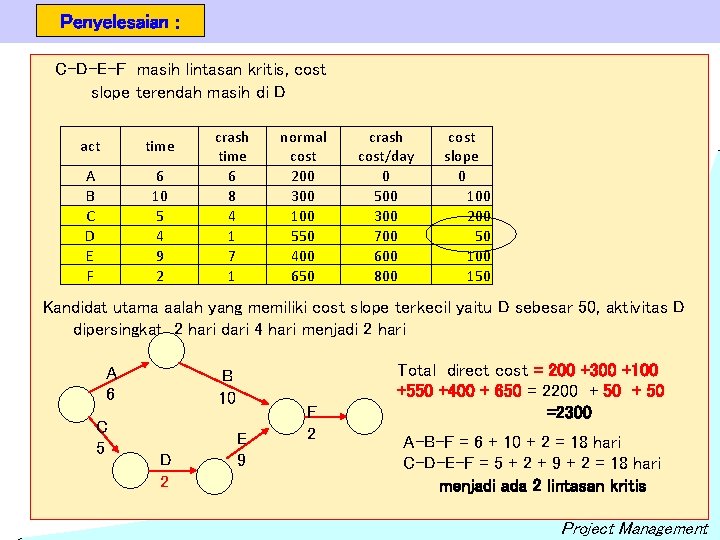
Penyelesaian : C-D-E-F masih lintasan kritis, cost slope terendah masih di D act time A B C D E F 6 10 5 4 9 2 crash time 6 8 4 1 7 1 normal cost 200 300 100 550 400 650 crash cost/day 0 500 300 700 600 800 cost slope 0 100 200 50 100 150 Kandidat utama aalah yang memiliki cost slope terkecil yaitu D sebesar 50, aktivitas D dipersingkat 2 hari dari 4 hari menjadi 2 hari A 6 C 5 B 10 D 2 E 9 F 2 Total direct cost = 200 +300 +100 +550 +400 + 650 = 2200 + 50 =2300 A-B-F = 6 + 10 + 2 = 18 hari C-D-E-F = 5 + 2 + 9 + 2 = 18 hari menjadi ada 2 lintasan kritis Project Management

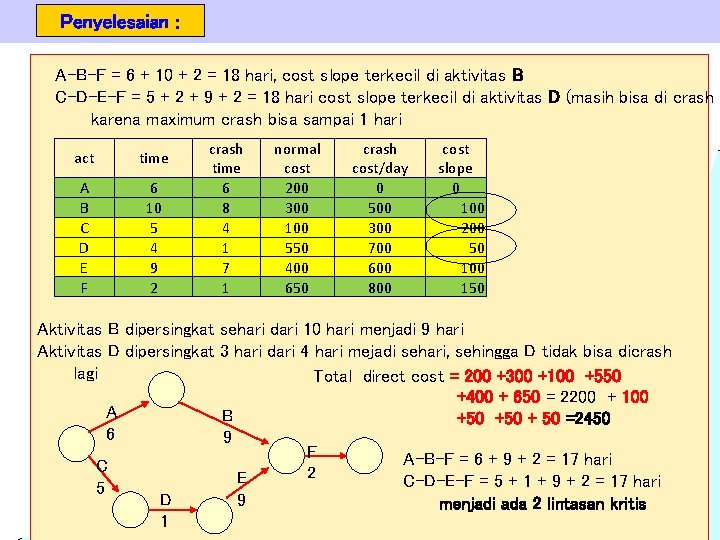
Penyelesaian : A-B-F = 6 + 10 + 2 = 18 hari, cost slope terkecil di aktivitas B C-D-E-F = 5 + 2 + 9 + 2 = 18 hari cost slope terkecil di aktivitas D (masih bisa di crash karena maximum crash bisa sampai 1 hari act time A B C D E F 6 10 5 4 9 2 crash time 6 8 4 1 7 1 normal cost 200 300 100 550 400 650 crash cost/day 0 500 300 700 600 800 cost slope 0 100 200 50 100 150 Aktivitas B dipersingkat sehari dari 10 hari menjadi 9 hari Aktivitas D dipersingkat 3 hari dari 4 hari mejadi sehari, sehingga D tidak bisa dicrash lagi Total direct cost = 200 +300 +100 +550 +400 + 650 = 2200 + 100 A B +50 + 50 =2450 6 9 F A-B-F = 6 + 9 + 2 = 17 hari C 2 E C-D-E-F = 5 + 1 + 9 + 2 = 17 hari 5 D 9 menjadi ada 2 lintasan kritis 1 Project Management

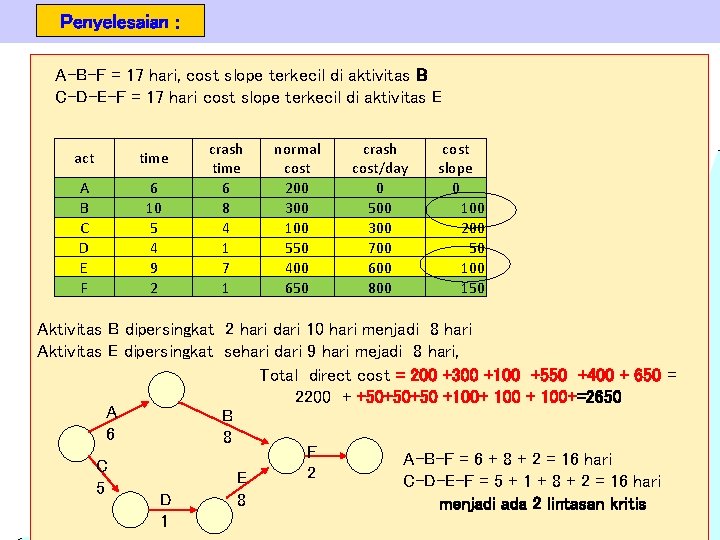
Penyelesaian : A-B-F = 17 hari, cost slope terkecil di aktivitas B C-D-E-F = 17 hari cost slope terkecil di aktivitas E act time A B C D E F 6 10 5 4 9 2 crash time 6 8 4 1 7 1 normal cost 200 300 100 550 400 650 crash cost/day 0 500 300 700 600 800 cost slope 0 100 200 50 100 150 Aktivitas B dipersingkat 2 hari dari 10 hari menjadi 8 hari Aktivitas E dipersingkat sehari dari 9 hari mejadi 8 hari, Total direct cost = 200 +300 +100 +550 +400 + 650 = 2200 + +50+50+50 +100+ 100+=2650 A B 6 8 F A-B-F = 6 + 8 + 2 = 16 hari C 2 E C-D-E-F = 5 + 1 + 8 + 2 = 16 hari 5 D 8 menjadi ada 2 lintasan kritis 1 Project Management

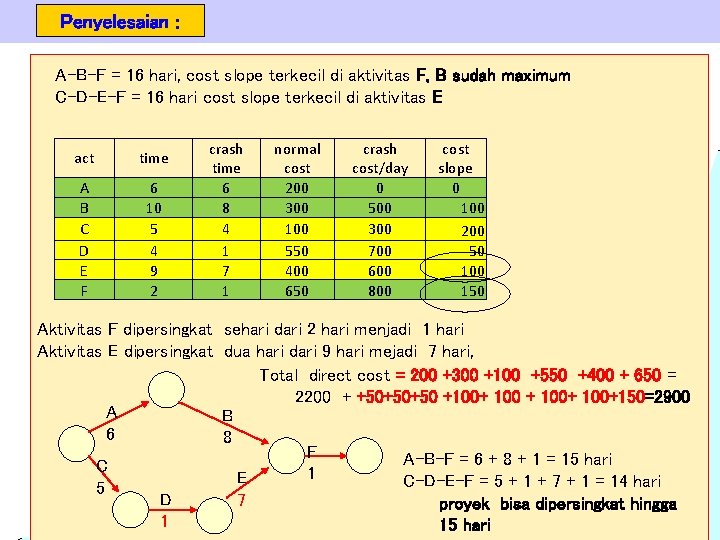
Penyelesaian : A-B-F = 16 hari, cost slope terkecil di aktivitas F, B sudah maximum C-D-E-F = 16 hari cost slope terkecil di aktivitas E act time A B C D E F 6 10 5 4 9 2 crash time 6 8 4 1 7 1 normal cost 200 300 100 550 400 650 crash cost/day 0 500 300 700 600 800 cost slope 0 100 200 50 100 150 Aktivitas F dipersingkat sehari dari 2 hari menjadi 1 hari Aktivitas E dipersingkat dua hari dari 9 hari mejadi 7 hari, Total direct cost = 200 +300 +100 +550 +400 + 650 = 2200 + +50+50+50 +100+ 100+150=2900 A B 6 8 F A-B-F = 6 + 8 + 1 = 15 hari C 1 E C-D-E-F = 5 + 1 + 7 + 1 = 14 hari 5 D 7 proyek bisa dipersingkat hingga 1 15 hari Project Management

Penyelesaian : Total cost = total direct cost + total indirect cost = 2900+(15 hari x 100) = 40400 durasi direct cost indirect total cost 20 19 18 17 16 15 2200 2000 2250 1900 2300 1800 2450 1700 2650 1600 2900 1500 4200 4150 4100 4150 4250 4400 Durasi normal 20 hari, jika dipersingkat sehari maka total costnya 4250 Jika dipersingkat 2 hari maka total costnya menjadi 4100 Project Management

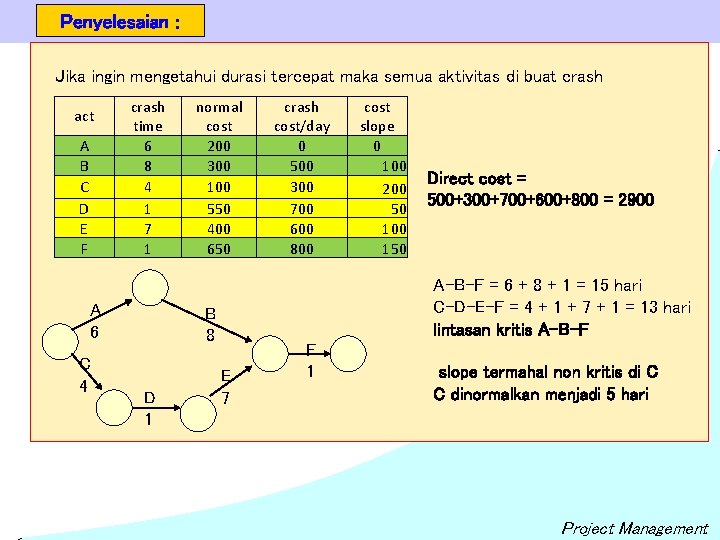
Penyelesaian : Jika ingin mengetahui durasi tercepat maka semua aktivitas di buat crash act A B C D E F crash time 6 8 4 1 7 1 A 6 C 4 normal cost 200 300 100 550 400 650 cost slope 0 100 200 50 100 150 Direct cost = 500+300+700+600+800 = 2900 A-B-F = 6 + 8 + 1 = 15 hari C-D-E-F = 4 + 1 + 7 + 1 = 13 hari lintasan kritis A-B-F B 8 D 1 crash cost/day 0 500 300 700 600 800 E 7 F 1 slope termahal non kritis di C C dinormalkan menjadi 5 hari Project Management

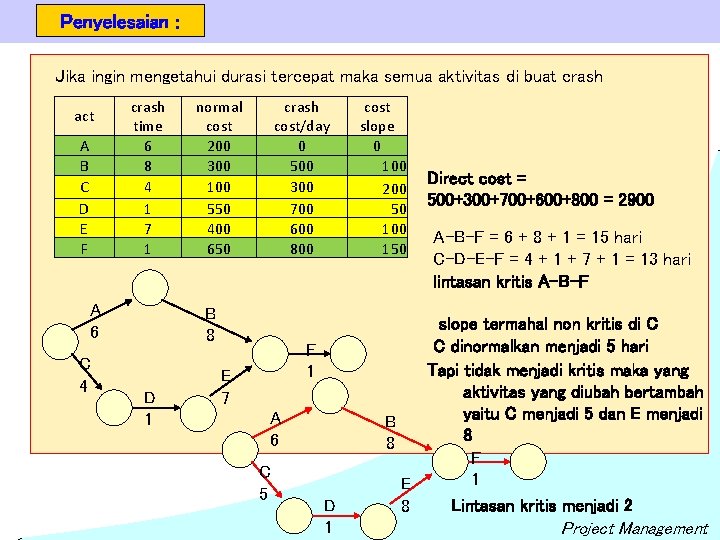
Penyelesaian : Jika ingin mengetahui durasi tercepat maka semua aktivitas di buat crash act A B C D E F crash time 6 8 4 1 7 1 A 6 C 4 normal cost 200 300 100 550 400 650 crash cost/day 0 500 300 700 600 800 B 8 D 1 F 1 E 7 A 6 C 5 D 1 cost slope 0 100 200 50 100 150 Direct cost = 500+300+700+600+800 = 2900 A-B-F = 6 + 8 + 1 = 15 hari C-D-E-F = 4 + 1 + 7 + 1 = 13 hari lintasan kritis A-B-F slope termahal non kritis di C C dinormalkan menjadi 5 hari Tapi tidak menjadi kritis maka yang aktivitas yang diubah bertambah yaitu C menjadi 5 dan E menjadi B 8 8 F 1 E Lintasan kritis menjadi 2 8 Project Management

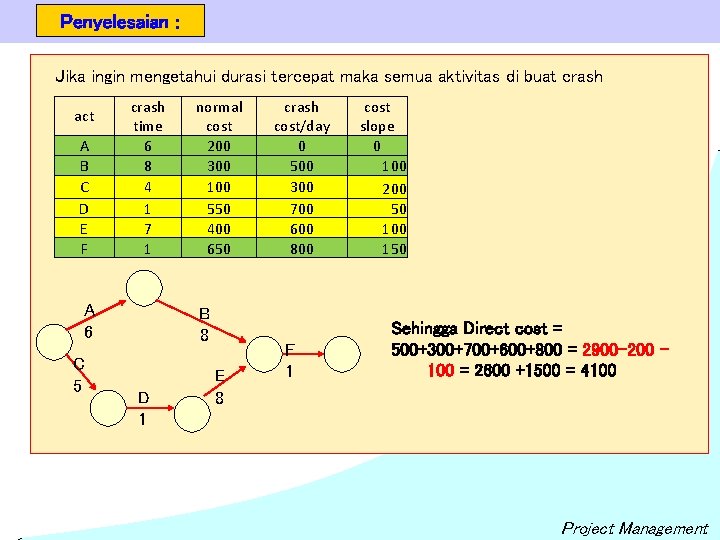
Penyelesaian : Jika ingin mengetahui durasi tercepat maka semua aktivitas di buat crash act A B C D E F crash time 6 8 4 1 7 1 A 6 C 5 normal cost 200 300 100 550 400 650 B 8 D 1 E 8 crash cost/day 0 500 300 700 600 800 F 1 cost slope 0 100 200 50 100 150 Sehingga Direct cost = 500+300+700+600+800 = 2900 -200 100 = 2600 +1500 = 4100 Project Management

Aggregat dan alokasi sumber Agregat Sumber adalah prosedur komparasi yang sederhana dan outputnya terdiri dari list atau histogram yang menunjukan kebutuhan total tiap sumber periodenya. Biasanya akan kelihatan apakah dengan agregat sumber tadi cukup memadai atau terjadi overload untuk dilaksanakan. Untuk itu bila overload maka bisa di-rescheduling atau ditambah sumber dayanya. Hal itu disebuat alokasi resources atau alokasi sumber : Prosedur yang umum : 1. Adanya agregat sumber 2. Identifikasi periode yang overload 3. Lakukan rescheduling : 1. Lihat Total Float 2. Jika over load, tambah sumber dayanya 3. Jika masih overload jalankan seterusnya. Project Management

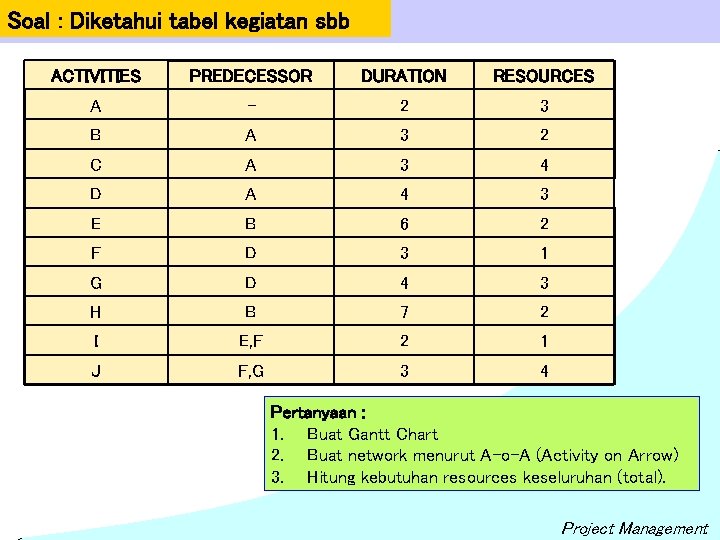
Soal : Diketahui tabel kegiatan sbb ACTIVITIES PREDECESSOR DURATION RESOURCES A - 2 3 B A 3 2 C A 3 4 D A 4 3 E B 6 2 F D 3 1 G D 4 3 H B 7 2 I E, F 2 1 J F, G 3 4 Pertanyaan : 1. Buat Gantt Chart 2. Buat network menurut A-o-A (Activity on Arrow) 3. Hitung kebutuhan resources keseluruhan (total). Project Management

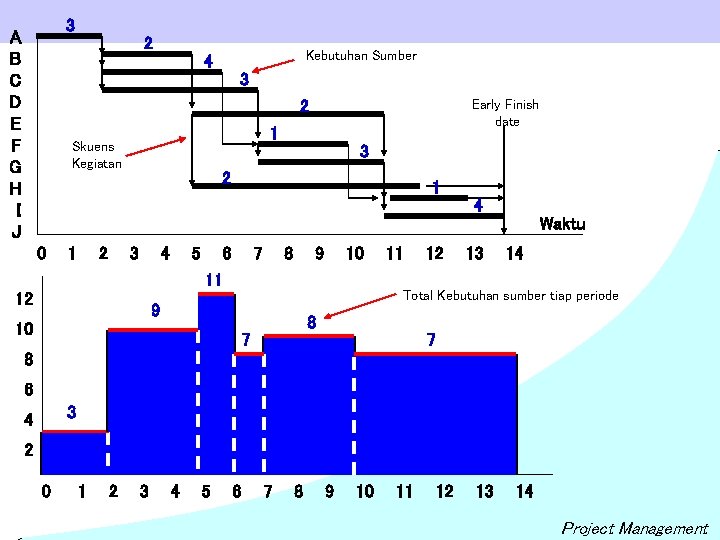
3 A B C D E F G H I J 2 Kebutuhan Sumber 4 3 2 Early Finish date 1 Skuens Kegiatan 3 2 1 4 Waktu 0 1 2 3 4 12 5 6 11 7 8 9 10 11 12 13 14 Total Kebutuhan sumber tiap periode 9 8 10 7 7 8 6 3 4 2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Project Management

Project Management